自动步枪刚性抛壳可靠性分析与设计方法研究

邹衍， 徐诚， 罗少敏， 杨洋

(南京理工大学 机械工程学院， 江苏 南京 210094)

自动步枪刚性抛壳可靠性分析与设计方法研究

邹衍， 徐诚， 罗少敏， 杨洋

(南京理工大学 机械工程学院， 江苏 南京 210094)

动作可靠性是机构设计中必须考虑的重要因素，也是衡量系统质量好坏的关键指标。为研究自动步枪抛壳机构的动作可靠性，确立了影响抛壳动作可靠性的主要影响参数，建立了一套自动步枪刚性抛壳可靠性分析与设计流程。构建了刚性抛壳动作可靠性简化虚拟样机模型，通过仿真表明抛壳挺位置、抛壳窗后挡板位置和抛壳速度是影响抛壳动作可靠性的主导因素；自动机速度足够大时，重力对抛壳动作可靠性的影响较小；给出了抛壳挺位置确定方法，确立了抛壳窗定位尺寸的取值方程，为自动步枪结构设计提供了参考和依据。还设计了一套可调节抛壳窗后挡板位置的装置并进行射击实验，实验结果与动作可靠性仿真结果一致，表明该方法有效性和适用性较好，具有一定的理论意义和工程应用价值。

兵器科学与技术； 自动武器； 动作可靠性； 可靠性分析； 刚性抛壳

0 引言

机构动作可靠性是指机构在规定的使用条件下，在规定的使用时间内，精确、及时、协调地完成规定动作(运动)的能力，用概率表示就是机构动作可靠度[1]。动作可靠性是所有机构设计中必须考虑的因素，也是决定机构成功与否的关键所在。

在兵器系统领域，动作可靠性是兵器性能的重要指标，直接影响到兵器的使用和战时勤务。国内学者对此进行了初步研究并取得了一定的成果。程刚等[2]基于多体动力学仿真的动作可靠性分析方法，进行了拨弹轮初始定位角误差对拨弹动作可靠性仿真分析，并根据仿真结果对结构进行了优化。李伟等[3]利用机械系统动力学自动分析Adams软件与控制系统和多学科动态系统Easy5软件建立了供输弹系统机电液耦合的动力学模型并进行了可靠性分析，为复杂系统动作可靠性的评估提供了新的思路。赫雷等[4]为研究某自动武器弹性抛壳机构的工作可靠性，利用Adams软件建立的虚拟样机模型，研究得到了不同的抛壳挺簧力、自动机后坐速度对弹壳运动状况的影响规律，为该机构的结构设计提供了理论依据。卡壳故障是自动步枪常见的典型故障，目前国内外对其进行理论研究较少，尚未建立成熟的枪械抛壳可靠性分析与设计方法。

本文以自动步枪刚性抛壳机构为研究对象，确立了影响抛壳动作可靠性的主要影响参数，建立了一套刚性抛壳可靠性分析与设计方法。利用Adams软件，建立了虚拟样机模型。利用仿真方法研究了主要影响参数对抛壳动作可靠性影响，并根据仿真分析结果确立了抛壳窗定位尺寸的取值方程。最后利用实验，对仿真分析结果进行了验证。

1 抛壳动作可靠性分析与设计方法

1.1 研究对象

自动步枪的抛壳方式一般分为两种：刚性抛壳和弹性抛壳[5]，其中刚性抛壳是我国自动步枪常用的抛壳方式。步枪刚性抛壳机构示意图如图1所示。模型共7个零件，包括弹壳、机头、拉壳钩、拉壳钩簧、抛壳挺、下机匣和抛壳窗后挡板。抛壳基本动作为：机头与拉壳钩配合，在火药燃气的作用下带动弹壳向后运动；当弹壳底部与抛壳挺碰撞后，弹壳与机头、拉壳钩脱离向斜后方抛出；弹壳飞出一段距离后，与抛壳窗后挡板碰撞，之后改变方向，弹壳向斜前方抛出。整个过程中弹壳不与下机匣接触。

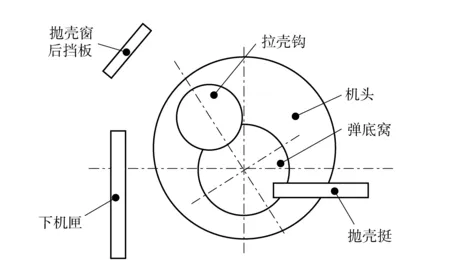
图1 抛壳机构示意图(沿枪管轴线观察)Fig.1 Schematic diagram of ejection mechanism (viewing along the axis of barrel)

1.2 抛壳动作可靠性主要影响参数

影响步枪抛壳的结构参数较多，如图2所示为可能影响抛壳动作可靠性的结构参数示意图。

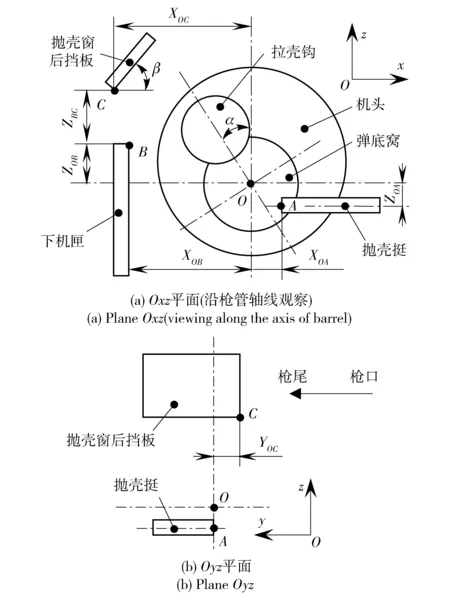
图2 抛壳机构结构参数示意图Fig.2 Structural parameters of ejection mechanism

点O、点A、点B和点C分别为机头、抛壳挺、下机匣和抛壳窗后挡板的定位基准点。以点O为整个模型基准点，在Oyz平面内，点O与点A共线。模型定位尺寸包括XOA、ZOA、XOB、ZOB、XOC、YOC和ZBC共7个长度变量，以及α、β共2个角度变量。XOA为抛壳挺定位点A沿x轴到模型基准点O的距离，ZOA为抛壳挺定位点A沿z轴到模型基准点O的距离。XOB、ZOB、XOC、YOC和ZBC定义以此类推。α和β分别为机头上拉壳钩孔中心与弹底窝中心连线与竖直线的夹角和抛壳窗后挡板倾角。由于实际工作中，抛壳挺、下机匣和抛壳窗后挡板为固定件，机头为活动件，故模型定位尺寸在取值时需要考虑枪机框与导轨、机头等之间的间隙。通过合理设置各个定位尺寸的取值范围，即可模拟自动步枪实际工作状况。如XOA和ZOA取值范围需要考虑抛壳挺结构尺寸、枪机框与导轨间隙以及弹壳与弹底窝间的间隙。

由于弹药装药误差及部件间间隙的随机性，使得抛壳速度v是一个变化量。抛壳速度v的变化对步枪抛壳的影响不应忽略。拉壳钩与机头间通过转动副和拉壳钩簧连接。拉壳钩簧的刚度k和预压力F0的大小直接影响抱弹及抛壳，抛壳动作可靠性研究同样需考虑拉壳钩簧刚度k和预压力F0的影响。

综合刚性抛壳机构结构参数和其他影响因素，本文共确定12个主要影响参数作为刚性抛壳动作可靠性分析参数，如表1所示。12个主要影响参数可以分为3类：速度参数、力学参数和结构参数。

表1 刚性抛壳动作可靠性主要影响参数表

1.3 动作可靠性分析与设计方法

为了更好地进行步枪刚性抛壳动作可靠性研究，本文提出了一套可靠性设计方法，其流程图如图3所示。

首先，根据实际需求，从表1中选取关心的主要影响参数并初步确定主要影响参数大致的取值范围，建立模型的虚拟样机，利用蒙特卡罗随机法进行大量仿真。然后，分析仿真结果，计算可靠度，判断是否满足要求。如果不满足，重新选择主要影响参数，重新开始设计；如果满足，即可确定抛壳挺定位尺寸，主要影响参数取值范围，同时拟合出抛壳窗定位尺寸公式。最后，在有条件的情况下进行样机实验，验证仿真结果，完成可靠性设计。

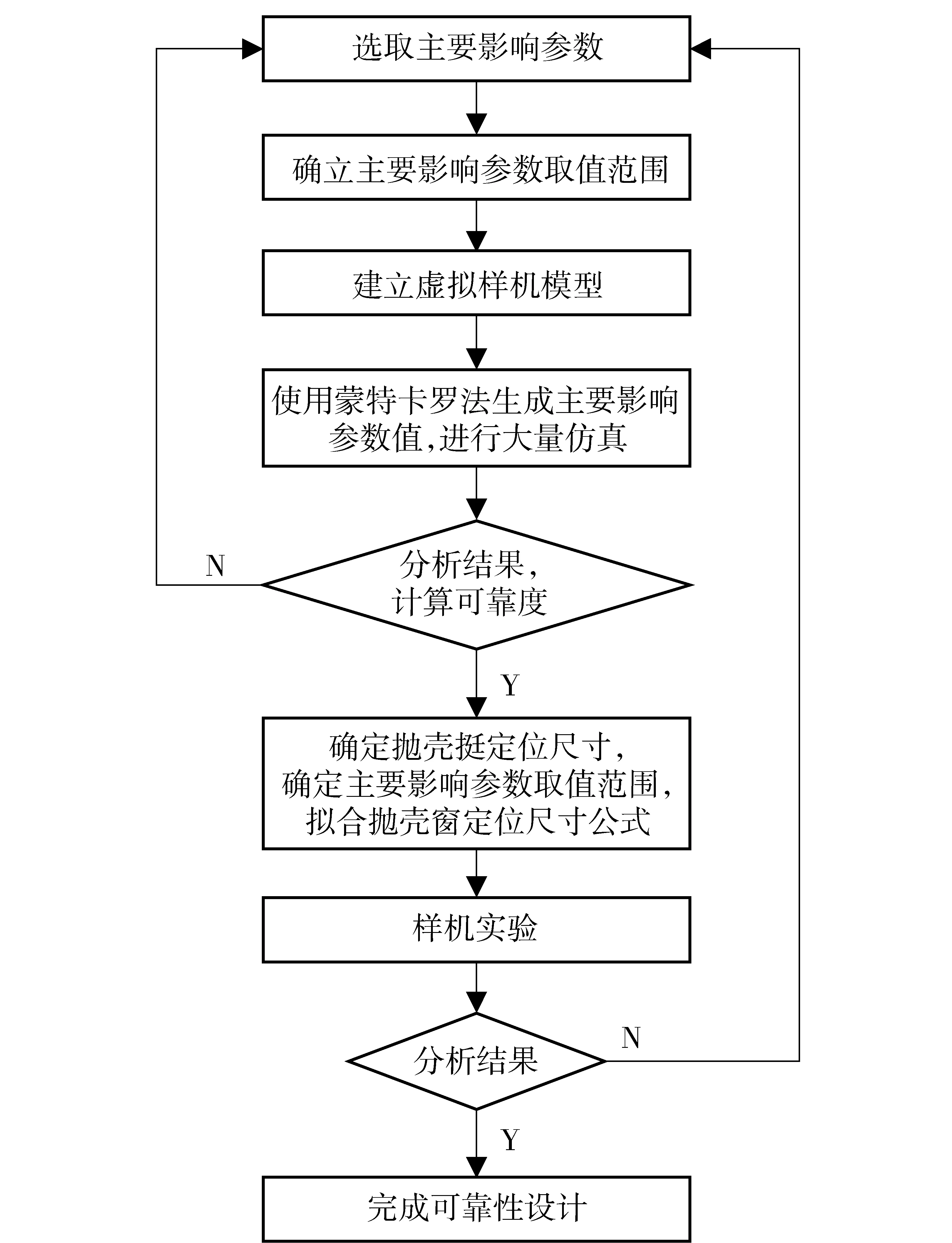
图3 刚性抛壳动作可靠性分析与设计方法流程图Fig.3 Flow chart of rigid ejection reliability analysis and design method

抛壳动作可靠一般指弹壳抛出机匣，不出现卡壳现象。因此，本文建立的抛壳可靠判据如下：

如图2所示，以点O为坐标原点，建立坐标系。在弹壳与抛壳挺碰撞后，弹壳运动时间t后，弹壳质心坐标为(x,y,z)，则弹壳抛壳可靠需满足几何关系如(1)式所示。

(1)

式中：X、Y、Z和l需根据枪械和弹壳结构确定的参数，|X|大于枪管轴线到机匣侧壁(抛壳方向)的距离，|Z|大于枪管轴线到机匣上端面的距离，|X|、|Z|和l保证弹壳抛出机匣，如图4所示，剖面线区域即为弹壳有效抛壳区域；L1和L2分别为弹壳质心到弹壳底部和头部的距离，L为弹壳全长，d为弹壳最大直径，如图5所示。对于同一时间t，|Y|越大，说明弹壳向前抛出趋势越明显。

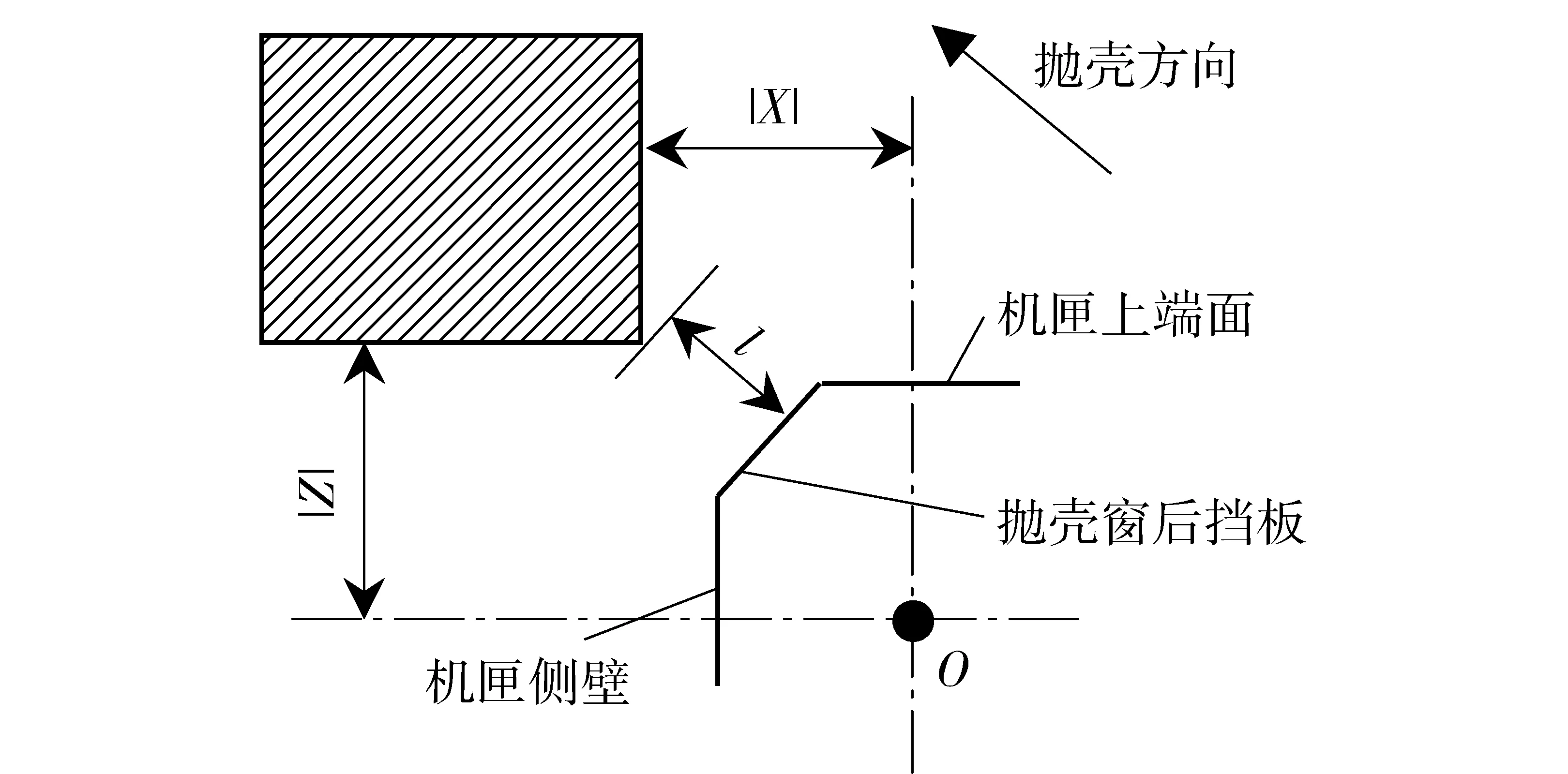
图4 有效抛壳区域示意图Fig.4 Schematic diagram of valid ejection area

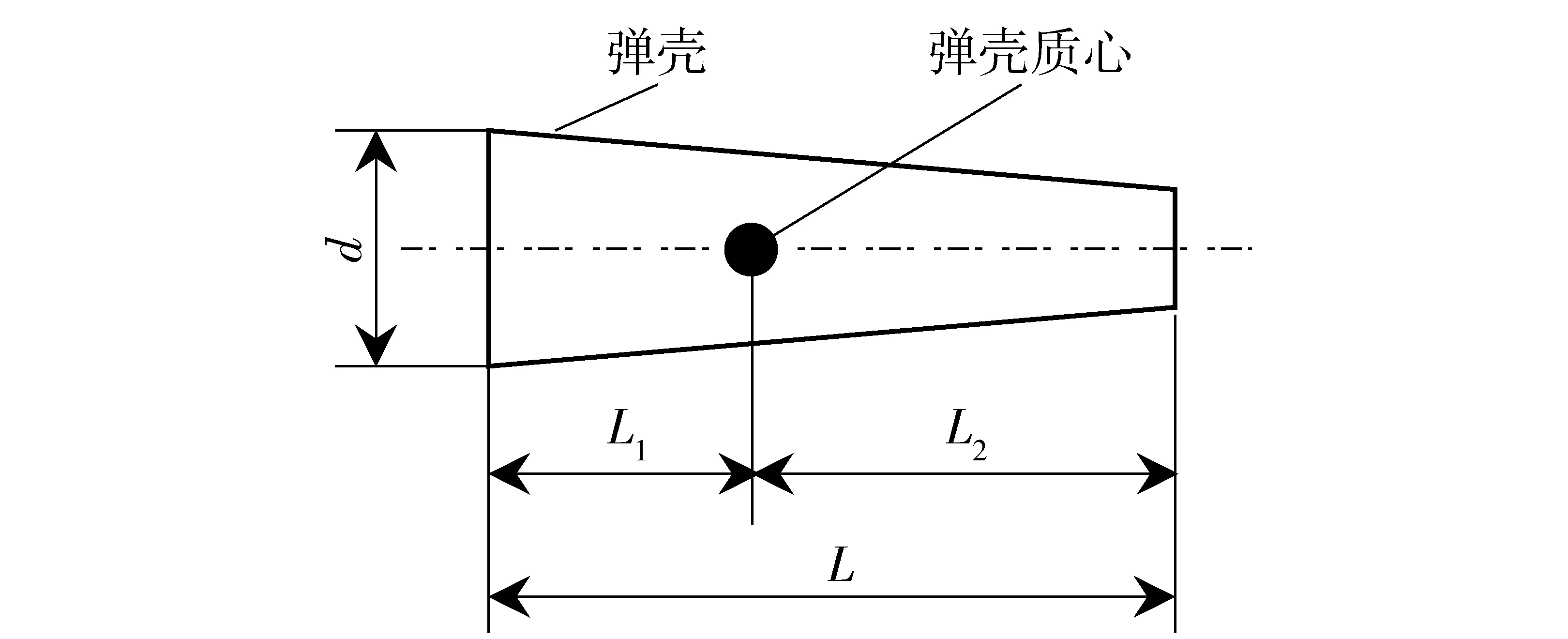
图5 弹壳示意图Fig.5 Schematic diagram of cartridge case

2 方法的实例应用

2.1 主要影响参数取值范围的确立

为了全面研究某自动步枪刚性抛壳动作可靠性，选定全部的12个主要影响参数进行可靠性研究。

对于抛壳速度的取值，本文通过实验，获取了某成熟自动步枪的抛壳速度参数，然后对其范围适当的扩充，得到实验取值范围。

将某自动步枪固定在枪架上，利用高速摄像系统拍摄自动机的枪机框运动过程，通过图像识别获取枪机框上标识点的位移数据，通过微分即可获得枪机框速度曲线。

实验共采集到43发弹发射的数据。对其抛壳速度统计，结果如图6和表2所示。

表2 抛壳速度统计表

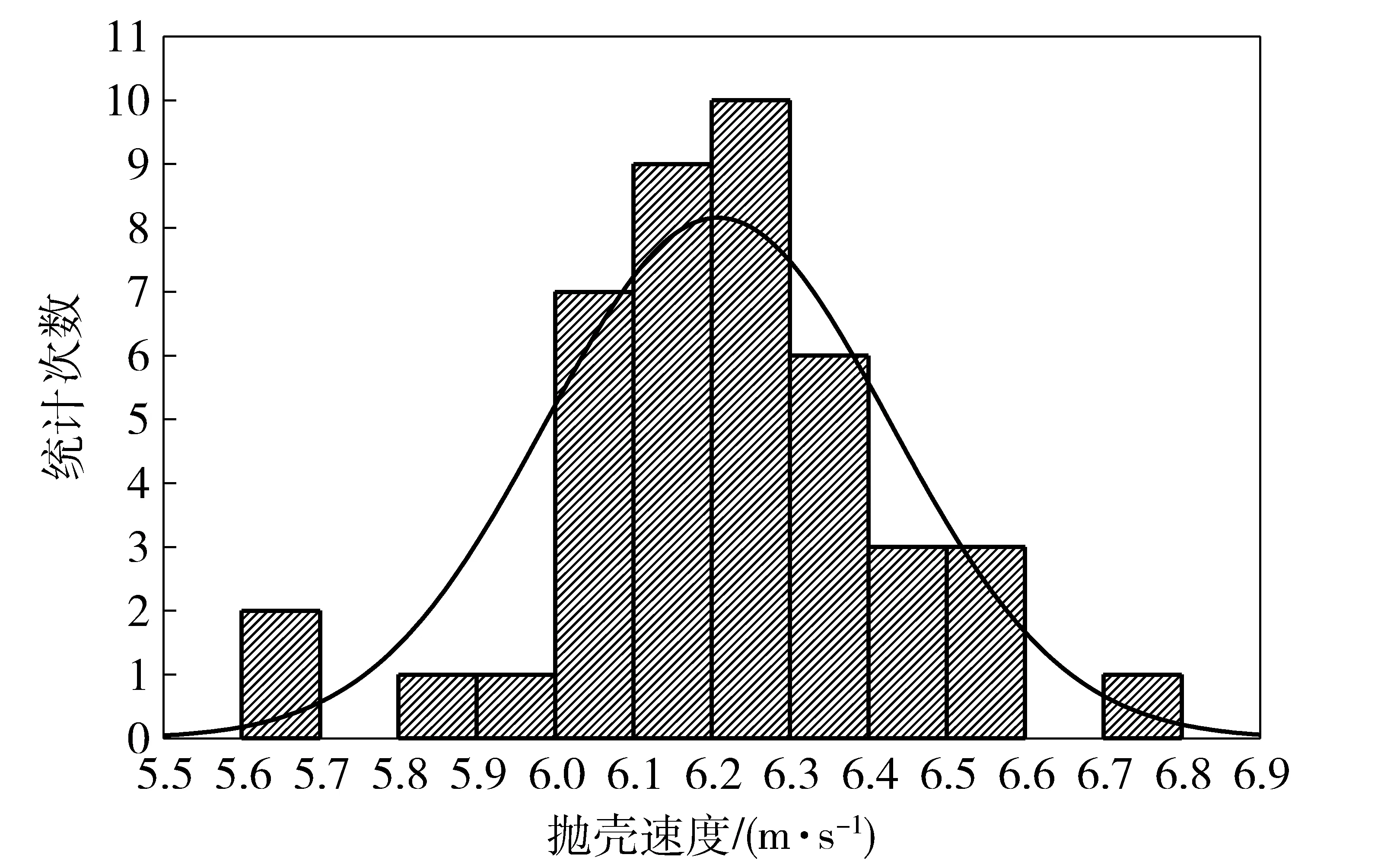
图6 抛壳速度直方图Fig.6 Histogram of ejection velocity

由图6和表2可知，抛壳速度的Shapiro-Wilk正态校验P值大于0.05，故其分布可认为符合正态分布，均值大小为6.2 m/s. 考虑到样本数量较少，以及极端情况的存在，故抛壳速度取值范围确定为[4.0 m/s,8.0 m/s]。

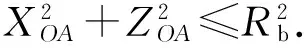
由于构件配合处常常设有间隙，故对于结构参数Xi在工作过程中，其尺寸参数是个随机变化的量，仿真时设置其取值范围为[90%Xi,110%Xi]，Xi表示各个参数设计值。

对于其他主要影响参数，参考现有设计方法，对其取值范围作相应扩充。所有主要影响参数取值范围如表3所示。

表3 主要影响参数取值范围表

2.2 虚拟样机模型的建立

本文利用Adams软件建立了步枪刚性抛壳虚拟样机模型，如图7所示。

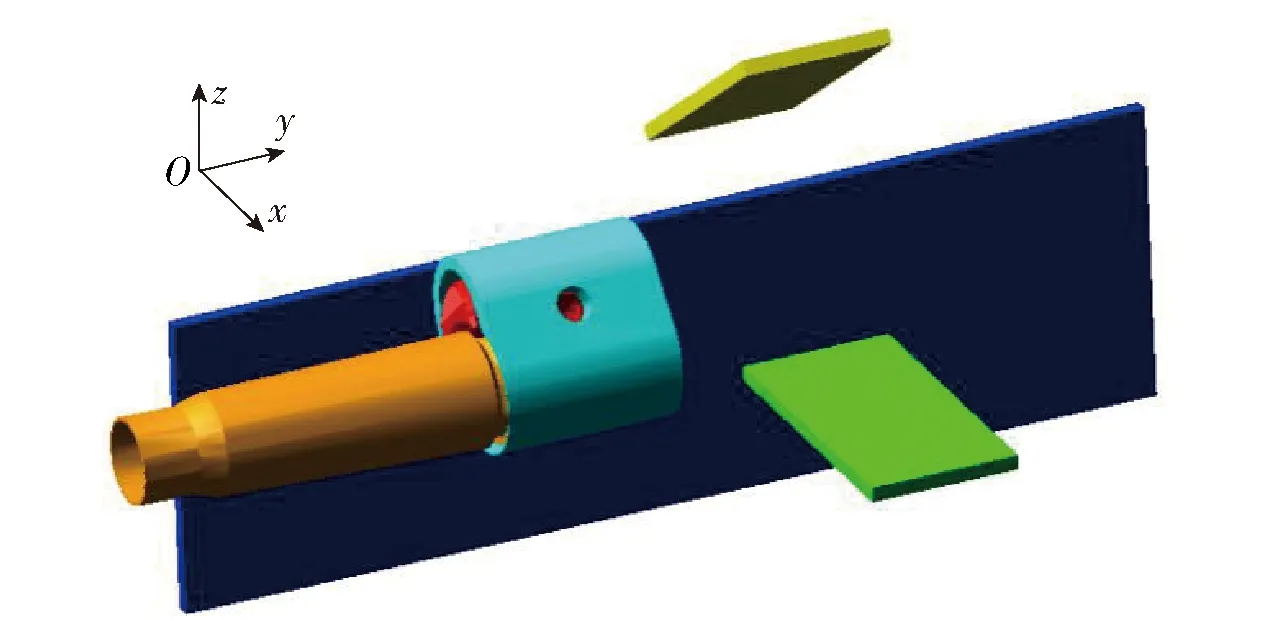
图7 虚拟样机模型图Fig.7 Model of virtual prototype

模型包括6个刚体：弹壳、机头、拉壳钩、抛壳挺、下机匣和抛壳窗后挡板；1个弹簧：拉壳钩簧(添加于拉壳钩与机头间)；2个旋转驱动：分别控制机头上拉壳钩孔中心与弹底窝中心连线与竖直线的夹角α和抛壳窗后挡板倾角β；1个线性驱动：添加于机头和大地间，用于控制抛壳速度；3个参数化点：分别对应点A、点B和点C，用于调节结构尺寸。弹壳与机头、拉壳钩、抛壳挺和抛壳窗后挡板间添加接触副(弹壳与下机匣间未添加接触副以便于观察弹壳飞行方向)。模型中重力方向为沿z轴向下。

2.3 仿真结果与分析

根据表3，利用Adams软件中的Insight[6]模块对建立的虚拟样机模型进行仿真分析。仿真采用蒙特卡罗法[7]根据取值范围随机生成主要影响参数值，主要影响参数分布采用均匀分布。仿真共进行了1 000次。

弹壳与抛壳挺接触后0.01 s，弹壳质心位置如图8所示。

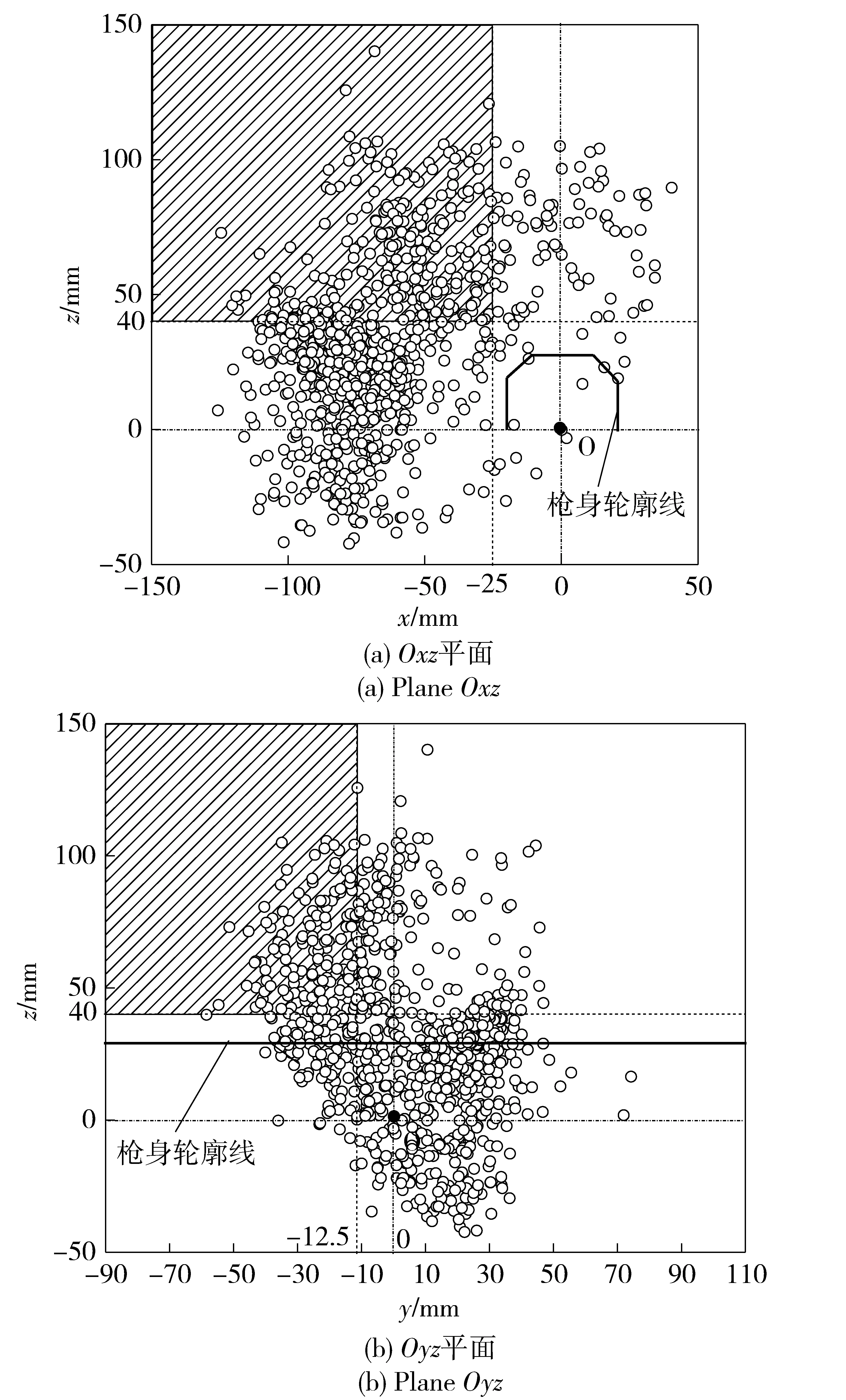
图8 弹壳质心位置图Fig.8 Center of mass positions of cartridge case

图8中，有剖面线的区域为根据抛壳可靠判据定义的满足抛壳要求的有效区域(x<-25 mm,y<-12.5 mm,z>40 mm)。从图8可知，仅有部分结果满足抛壳要求，统计分析可得，满足抛壳要求的次数仅为42次。

对抛壳挺定位点A的位置绘图，如图9所示。

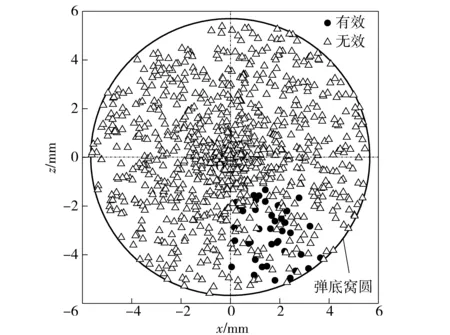
图9 抛壳挺定位点位置图Fig.9 Locating point positions of ejector

由图9可知，满足抛壳要求的抛壳挺定位点全部位于第四象限。抛壳时拉壳钩位于第二象限，由此可知，对于刚性抛壳，为保证抛壳可靠性，抛壳挺设计时应与拉壳钩呈对称分布。

根据上述结论确定抛壳挺位置，其他参数保持不变，重新进行1 000次仿真。根据仿真结果，绘制YOC、XOC、k和v的直方图如图10～图13所示。

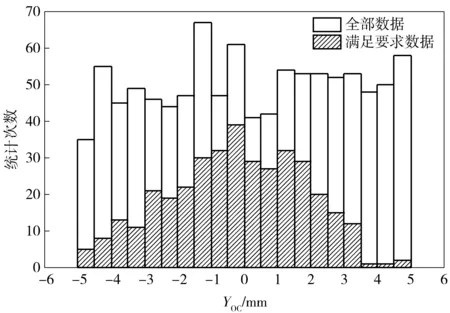
图10 YOC直方图Fig.10 Histogram of YOC

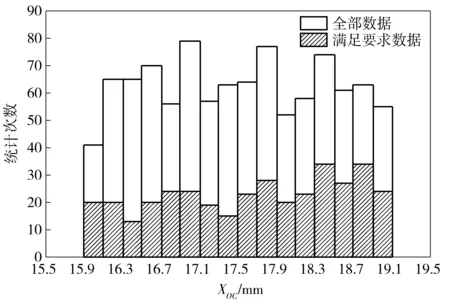
图11 XOC直方图Fig.11 Histogram of XOC

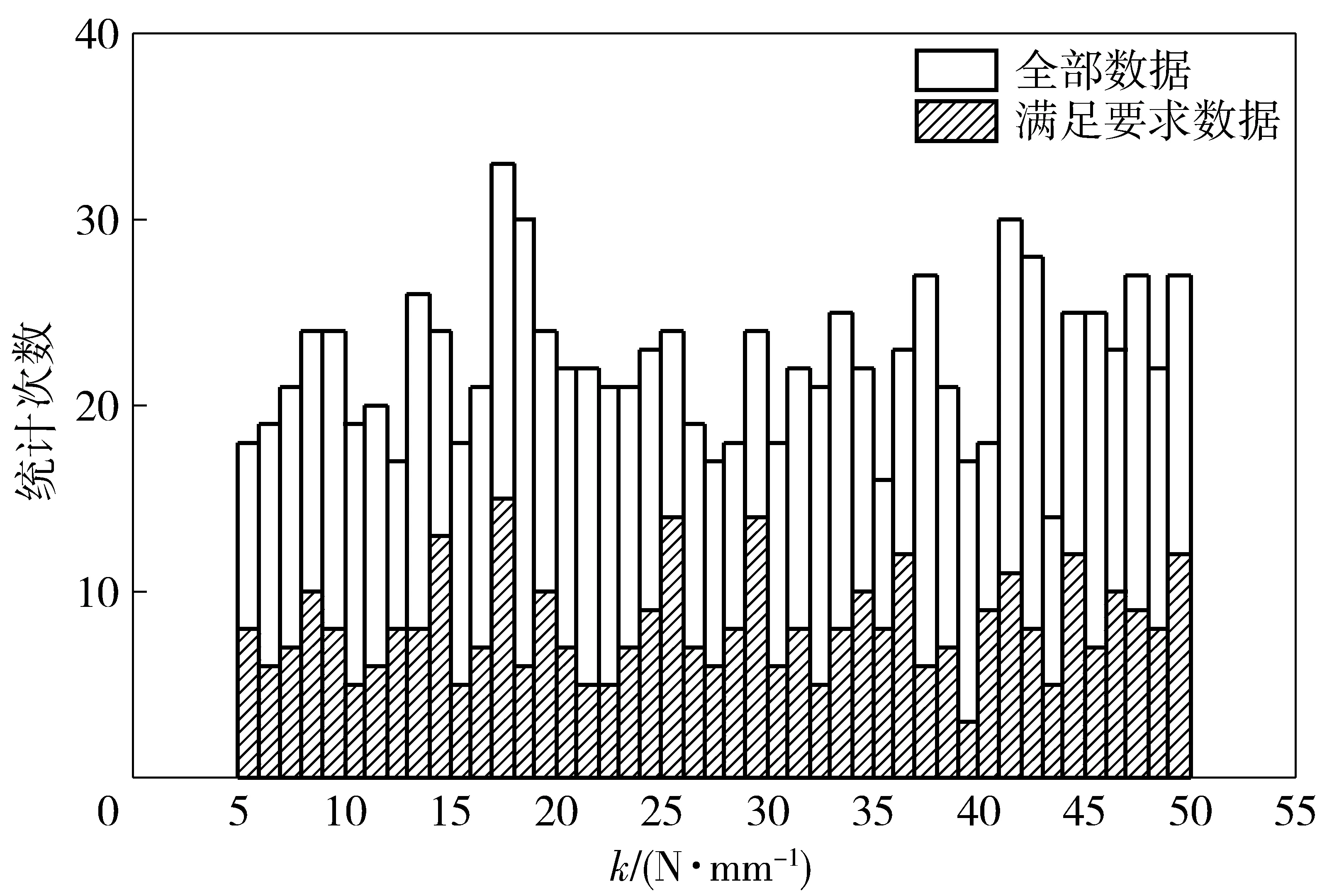
图12 k直方图Fig.12 Histogram of k

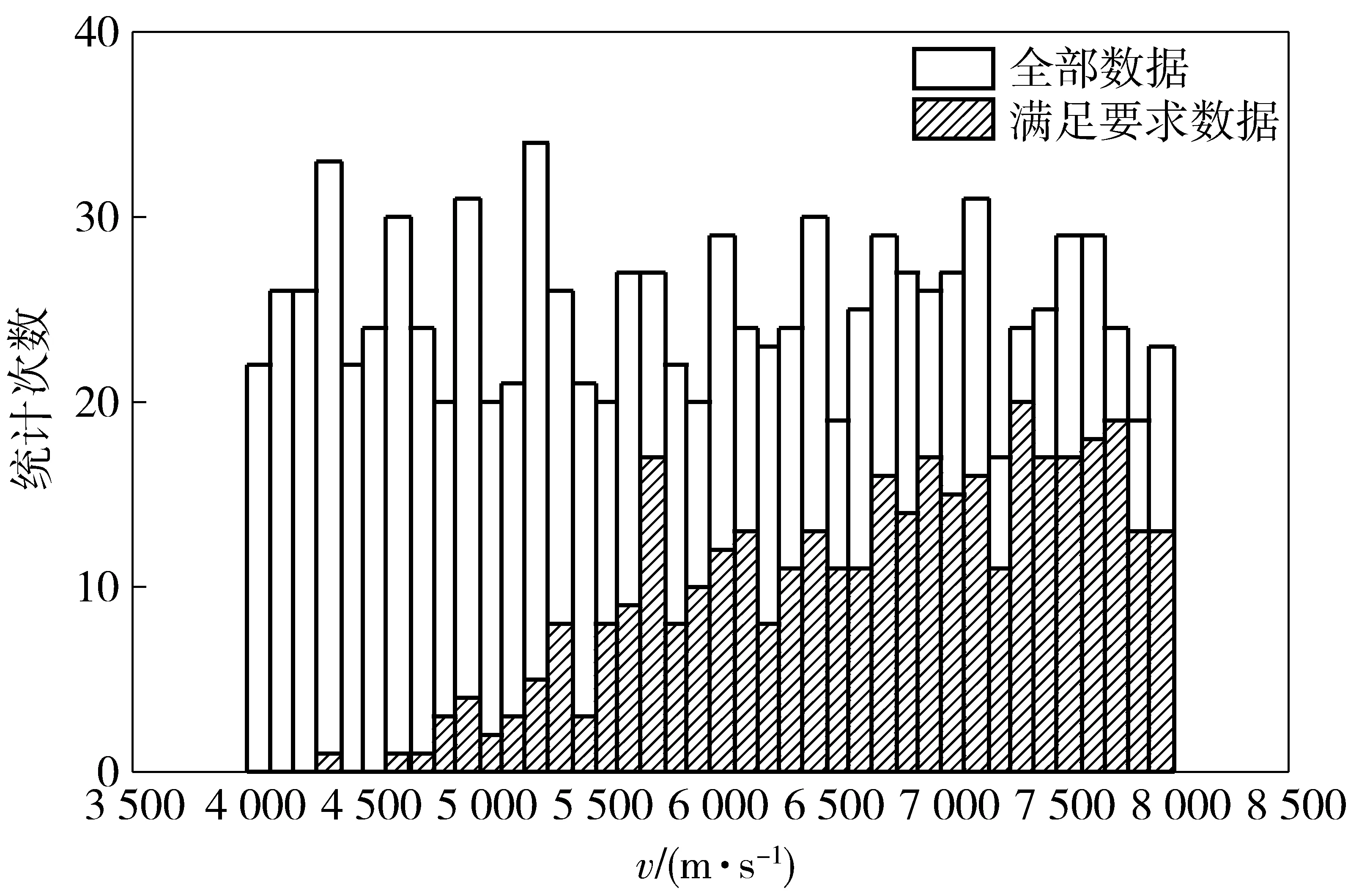
图13 v直方图Fig.13 Histogram of v

由图10可知，YOC的大小变化对抛壳动作可靠性影响较明显，当YOC取值越远离设计值0时，抛壳失误次数越多，动作可靠性越低。由图11和图12可知，在仿真取值范围内，XOC和拉壳钩刚度k满足抛壳要求的次数与总次数的分布类似，基本符合均匀分布，可见其大小对抛壳动作可靠性的影响较小，不是主要因素。其他未列出主要影响参数的直方图与图11和图12类似。由图13可知：当抛壳速度v较小时(v<5.5 m/s)，抛壳的成功率很低；当抛壳速度v较大时(v>5.5 m/s)，满足抛壳要求的次数分布规律与图11和图12类似。由此可见，抛壳速度v较小时对抛壳动作可靠性影响较明显。

下面着重研究YOC对抛壳动作可靠性的影响。重新设置主要影响参数的取值范围，除YOC和v外，其他参数取值范围调整为[95%Xi,105%Xi]，使各参数取值更接近实际工作值。v取值范围变为[5.3 m/s,7.0 m/s]，YOC取值范围及仿真结果如表4所示。

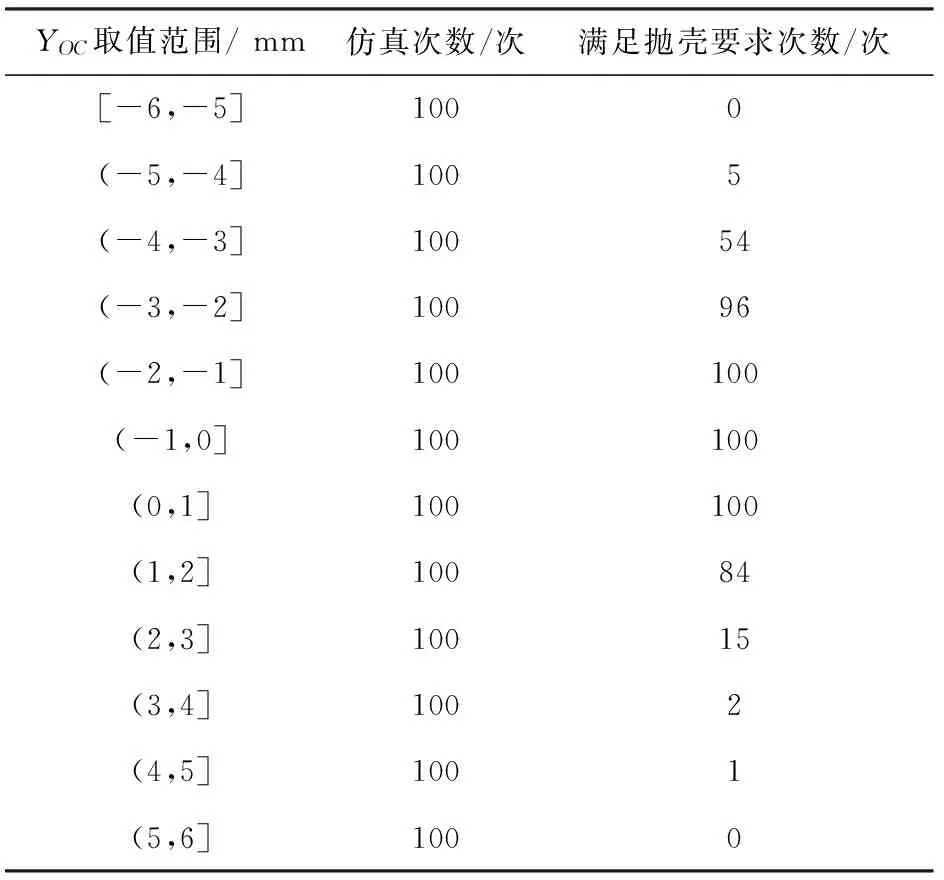
表4 YOC取值范围及仿真结果表

将满足抛壳要求的次数与仿真次数的比值定义为关于YOC的抛壳动作可靠度，显然可靠度越接近1，抛壳动作可靠性越好。关于YOC的可靠度曲线图如图14所示。

图14 关于YOC的可靠度曲线图Fig.14 Reliability curve about YOC

由表4和图14可知，当YOC改变时，抛壳成功率呈阶梯式变化，在远离0 mm处有较大的阶跃变化，接近0 mm处跳跃较小。当YOC取值为(-2 mm,1 mm)时，抛壳可靠度为1. 当YOC小于-4 mm或大于3 mm时，抛壳可靠度几乎为0. 进一步分析可知，当YOC小于-4 mm时失效包括两种情况：弹壳向斜前抛出，但过于靠近枪身；与抛壳后挡板碰撞后再次与下机匣碰撞，弹壳滞留在枪身内或过于靠近枪身。当YOC大于3 mm时，弹壳向斜后方抛出或者向前抛出趋势不明显。故为了保证步枪抛壳动作可靠性，YOC的取值应保证在(-2 mm,1 mm)内。

步枪在使用过程中，步枪的姿态是多种多样的，枪管轴线并不一定保持水平。在枪械性能测试过程中一般会进行俯仰射击以验证步枪的可靠性。本文在上述仿真的基础上，考虑重力方向，即增设步枪射击的俯仰角为变量，其取值范围为[-90°,90°]。俯仰角大于0°枪口向上仰，等于90°时枪口竖直向上；俯仰角小于0°枪口向下俯，等于-90°时枪口竖直向下。在取值范围内俯仰角按均匀分布取值。

仿真共进行300次，仿真结果全部符合抛壳要求。考虑重力方向和不考虑重力方向弹壳与抛壳挺接触后0.01 s，弹壳质心位置平均值如表5所示。由表5可知，重力方向对最终弹壳质心位置影响较小，最大误差仅为4.45%. 所以，重力方向对抛壳动作可靠性的影响不大。

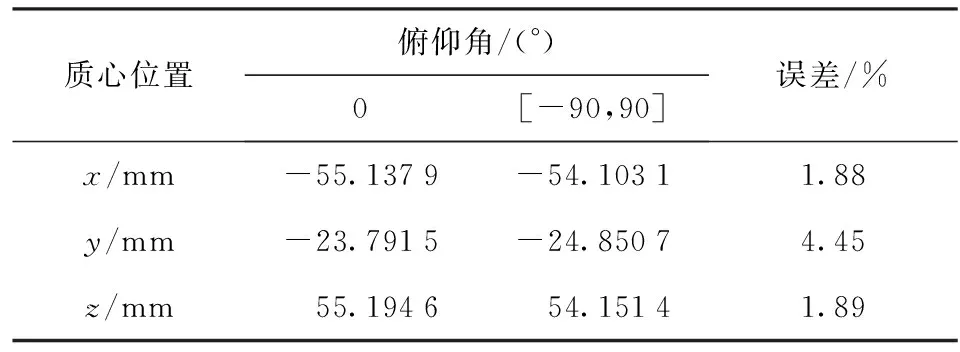
表5 弹壳质心位置平均值表

2.4 抛壳窗尺寸的确定

根据2.3节仿真结果，绘制弹壳质心位移曲线，如图15所示。

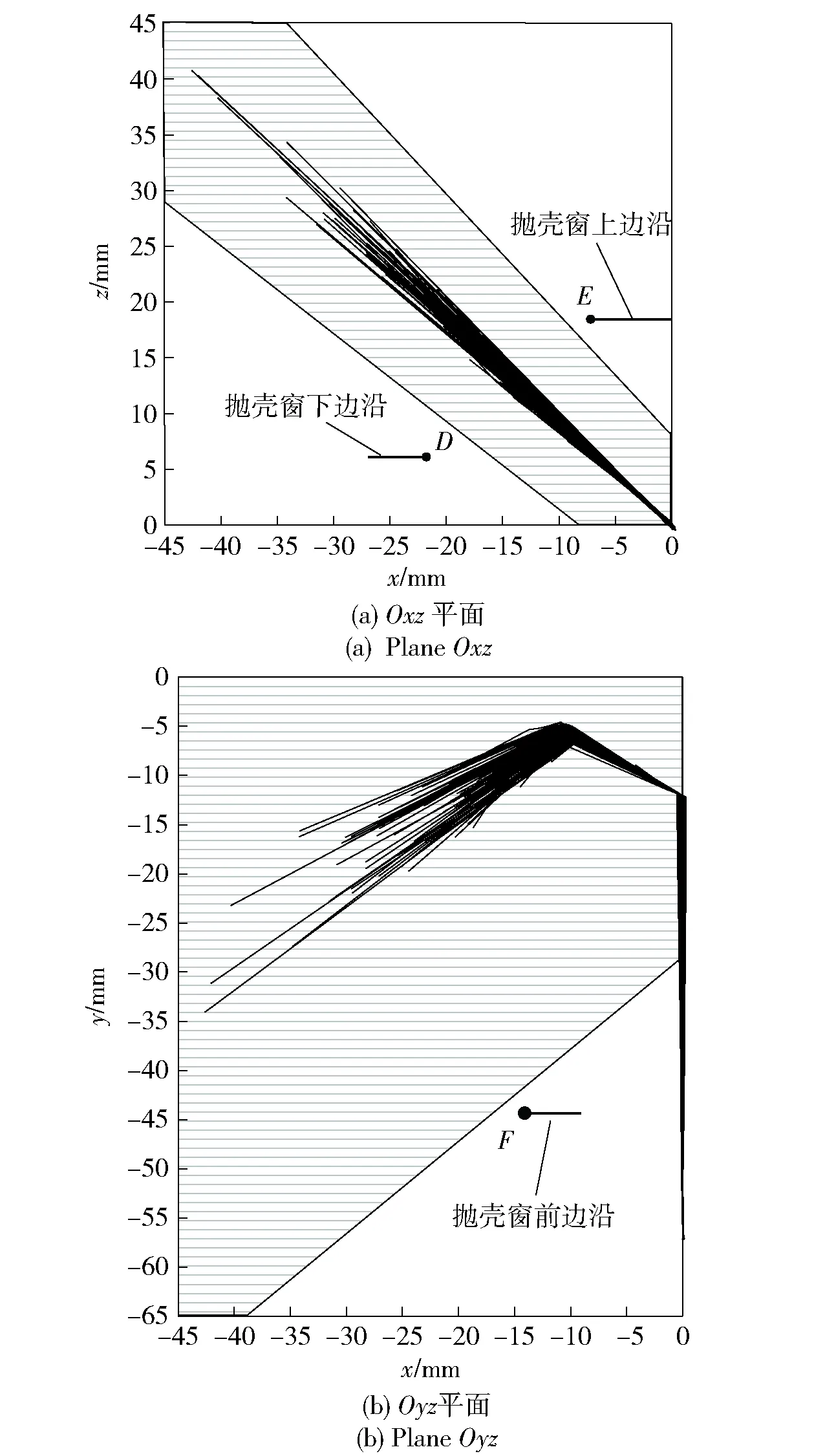
图15 弹壳质心位移曲线图Fig.15 Displacement diagram of center of mass of cartridge case

图15中，剖面线覆盖区域是根据弹壳外形尺寸和弹壳质心位置所确定的抛壳过程中弹壳运动包络面在相应平面的投影。点D、点E和点F分别为抛壳窗下边沿、上边沿和前边沿的定位点。

为了保证抛壳动作的可靠性，显然抛壳窗下边沿定位点D应位于图15(a)中的左下角空白区域，其定位尺寸关系式为

(2)

式中：θ1为弹壳质心平均抛壳轨迹在Oxz平面内的投影与z轴的夹角。同理，抛壳窗上边沿定位点E应位于图15(a)中的右上角空白区域，其定位尺寸关系式为

(3)

抛壳窗前边沿定位点F应位于图15(b)中的右下角空白区域，其定位尺寸关系式为

(4)

式中：θ2为弹壳与抛壳窗后挡板碰撞后弹壳质心平均抛壳轨迹在Oxy平面内的投影与y轴的夹角。

3 方法的实验验证

3.1 实验系统

根据仿真确立的抛壳窗尺寸控制方程，设计了一套可以调节抛壳窗后挡板位置的机构，其结构如图16所示。该机构包括：基座、纵杆、调节螺栓和抛壳窗后挡板。基座与横杆固连。抛壳窗后挡板设有螺栓槽，通过调节螺栓固定在横杆一侧。改变抛壳窗后挡板和调节螺栓间的相对位置即可实现抛壳窗后挡板沿横杆轴向的位置调整。该机构与自动步枪装配图如图17所示，实验时即可研究抛壳窗后挡板位置对抛壳的影响。

图16 可调节抛壳窗后挡板Fig.16 Adjustable backplate of ejection port

图17 实验自动步枪局部Fig.17 Partial diagram of experimental automatic rifle

实验对多组抛壳窗后挡板位置进行射击实验，并采用高速摄像系统进行数据采集，对各种工况下的抛壳结果进行统计分析。实验系统图如图18所示。

图18 实验系统图Fig.18 Experimental system

3.2 实验结果分析

通过高速摄像系统发现，结果出现3种典型的抛壳情况，如图19所示。图19中，弹壳状态1为弹壳碰撞抛壳挺后但未脱离拉壳钩的某一状态；状态2是弹壳碰撞抛壳窗后挡板状态；状态3～5为弹壳抛出抛壳窗的状态。状态1和状态3～5间的时间间隔相等，各图抛壳时长相等。

图19 实验抛壳状态图Fig.19 Experimental ejection

根据仿真结果，实验定义抛壳角度为30°～60°时，为有效抛壳状态。对实验结果进行统计，统计结果如表6所示。

根据表6，对比图14可知，YOC等于-4 mm和0 mm时，实验获得的可靠度与仿真计算结果相近，抛壳失效模式与仿真结果一致。实验出现1次卡壳状态，弹壳卡在枪机框和节套之间，如图20所示，说明弹壳与抛壳窗后挡板碰撞后弹壳滞留在枪身内，枪机框复进时被弹壳阻挡。YOC等于4 mm时，实验获得的可靠度大于仿真计算结果，且失效模式未出现斜后方抛壳状态。总体分析，实验结果较好地验证了仿真结果，验证了基于虚拟样机的刚性抛壳可靠性分析与设计方法的有效性和可行性。

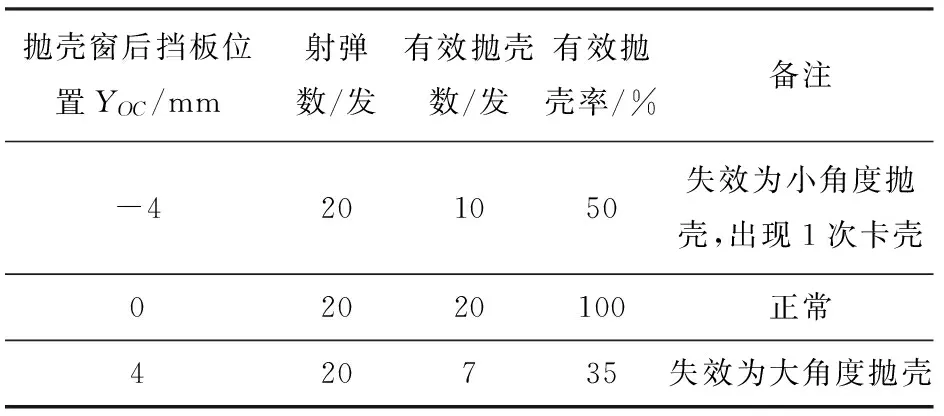
表6 抛壳实验结果统计表

图20 实验卡壳状态图Fig.20 Jamming of cartridge case

4 结论

通过本文的仿真与实验分析，主要得到如下主要结论：

1)以自动步枪刚性抛壳机构为研究对象，确立了影响抛壳动作可靠性的主要影响参数，建立了一套刚性抛壳动作可靠性分析与设计方法。

2)建立了自动步枪刚性抛壳动作可靠性虚拟样机简化模型。通过仿真分析发现，抛壳挺定位位置对抛壳动作可靠性有较大影响，为保证抛壳可靠性，抛壳挺应与拉壳钩呈对称分布。确立抛壳挺合理位置后，抛壳窗后挡板位置YOC和抛壳速度v是影响步枪抛壳动作可靠性的主导因素。抛壳动作可靠度随着YOC变化呈阶梯式变化，且远离0 mm处有较大的阶跃变化。当抛壳速度v较小时(v<5.5 m/s)，抛壳的成功率很低。在抛壳速度足够大时(v>5.5 m/s)，重力方向对抛壳动作可靠性的影响不大。给出了抛壳窗定位尺寸的确立方程，为类似步枪设计提供了参考。

3)设计了一套可调节抛壳窗后挡板位置的实验机构，完成了抛壳动作可靠性实验，实验结果与抛壳动作可靠性仿真结果吻合较好，验证了刚性抛壳可靠性分析与设计方法的有效性和可行性。

References)

[1] 何恩山, 孙志礼, 李良巧. 动作可靠性分析评价方法[J]. 东北大学学报:自然科学版, 2009,30(4): 589-592. HE En-shan, SUN Zhi-li, LI Liang-qiao. Analysis and evaluation of motion reliability[J]. Journal of Northeastern University:Natural Science, 2009, 30(4):589-592. (in Chinese)

[2] 程刚, 张相炎, 董志强. 供弹动作可靠性仿真研究[J]. 海军工程大学学报, 2011, 23(2): 72-75. CHENG Gang, ZHANG Xiang-yan, DONG Zhi-qiang. Motion reliability simulation research on feed mechanism[J]. Journal of Naval University of Engineering, 2011, 23(2): 72-75. (in Chinese)

[3] 李伟, 马吉胜, 狄长春, 等. 考虑参数随机性的供输弹系统动力学及动作可靠性仿真研究[J]. 兵工学报, 2012, 33(6): 747-752. LI Wei, MA Ji-sheng, DI Chang-chun, et al. Simulation research on dynamics of ramming system and action reliability considering the randomness of the parameters [J]. Acta Armamentarii, 2012, 33(6): 747-752. (in Chinese)

[4] 赫雷, 周克栋, 骆佳光, 等. 某自动武器弹性抛壳过程仿真分析[J]. 弹道学报, 2010, 22(3): 35-38. HE Lei, ZHOU Ke-dong,LUO Jia-guang, et al. Simulation analysis of elastic ejection process of some automatic weapon [J]. Journal of Ballistics, 2010, 22(3): 35-38.(in Chinese)

[5] 王裕安, 徐万和, 薄玉成. 自动武器构造[M]. 北京: 北京理工大学出版社, 1994. WANG Yu-an, XU Wan-he, BO Yu-cheng. Automatic weapons structure[M]. Beijing: Beijing Institute of Technology Press, 1994. (in Chinese)

[6] 李锦. 致命/非致命兼容发射装置性能分析与研究[D]. 南京:南京理工大学, 2016. LI Jin. Performance analysis and research on lethal and non-lethal compatibly launcher[D]. Nanjing: Nanjing University of Science and Technology, 2016. (in Chinese)

[7] Zio E. 可靠性与风险分析蒙特卡罗方法[M]. 赵宇，翟庆庆，译. 北京: 国防工业出版社, 2014. Zio E. The Monte Carlo simulation method for system reliability and risk analysis[M]. ZHAO Yu, ZHAI Qing-qing, translated. Beijing: National Defense Industry Press, 2014. (in Chinese)

Study of Rigid Ejection Reliability Analysis and Design Method of Automatic Rifle

ZOU Yan, XU Cheng, LUO Shao-min, YANG Yang

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)

The action reliability is an important factor which must be considered in the design of mechanisms, and is a key index to evaluate the quality of a system. The main parameters influencing ejection action reliability are determined, and a rigid ejection reliability analysis and design process of automatic rifles is set up. A simplified virtual prototype model of rigid ejection action reliability is established. The simulated results show that the position of ejector, the backplate position of ejection port and the ejection velocity are the dominant factors which have effect on ejection action reliability; as the ejection velocity is high enough, gravity has less effect on ejection action reliability. A method to determine the position of ejector is presented, and the calculational equations are established for location dimension of ejection port. An adjustable backplate of ejection port mechanism is designed to test in the shooting experiment. The experimental results are consistent with the simulated results. It shows that the validity and suitability of the proposed method are verified.

ordnance science and technology; automatic weapon; action reliability; reliability analysis; rigid ejection

2016-06-15

国家自然科学基金项目(51575279)

邹衍(1990—)，男，博士研究生。E-mail: nfzouyan@163.com

徐诚(1962—)，男，教授，博士生导师。E-mail: xucheng62@mail.njust.edu.cn

TJ22

A

1000-1093(2017)02-0209-09

10.3969/j.issn.1000-1093.2017.02.001