弹壳底部平底成形工艺优化

廖仕军,吕 刚,薛 松,孙 强,蒲 羽

(1.重庆长江电工工业集团有限公司， 重庆 401336；2.陆军装备部驻重庆地区第三军代室， 重庆 401336；3.陆军装备部驻泸州地区军代室，四川 泸州 646003)

运动弹弹壳的底部在平底成形过程中，通过在弹壳内腔底部设置内冲头，在弹壳壳体外部设置模具，内冲头和模具共同作用防止弹壳壳体在冲压过程中的变形，加工冲在高速冲压状态下完成弹壳底部的成形。目前国内的生产质量较国外同类型运动弹性能参数有较大差距，主要表现在速度、膛压、感度和射击功能可靠性等几个方面。

对于复杂冲压零部件多采用多次冲压成形来完成，目前国内外的相关报道主要针对冲压件型面过渡区域的拉伸、开裂等因素进行了分析，并在模具的改进方法上取得了一些进展[1-3]，研究的领域主要涉及汽车配件、轨道车等，其材料涉及领域包含不锈钢、铝合金等[4-6]合金材料，对于材料的回弹性主要通过软件模拟来进行工艺改进，对回弹产生的机理、制约因素和模具的优化方法等研究还有进一步的探索空间。此外，一些学者对材料冲压成形缺陷进行了分析和模拟，并对冲压件的使用寿命进行了分析和建模[7-10]，基于运动弹弹壳与不锈钢和铝合金的冲压过程存在类似性，以上缺陷分析和模拟方法对于运动弹弹壳的冲压建模具有重要的借鉴意义。在此基础上结合运用优化模型和优化算法将有效提升弹壳冲压仿真模拟的验证效率，大幅减少运动弹冲压实验次数和试验成本。

本文针对车间运动弹的底部成形工艺进行优化改进，通过对弹壳底部冲压模具和冲头冲压过程中，弹壳的受力变形和回弹量进行仿真分析，从而揭示出弹壳底部成形误差的起因，对弹壳底部过渡面的倒角应力集中和变形状态进行理论建模，基于该模型进行冲压工艺的优化和改进，从而使运动弹弹壳的生产质量基本达到和超过国外同类产品。

1 运动弹弹壳平底有限元模型

运动弹子弹材料为H68铜材，图1为平底前冲头、弹壳、限位冲和外模之间装配关系图，其中弹壳内部通过限位冲限制弹壳内部的自由度，弹壳外部通过外模具限制弹壳外部的自由度，弹壳内部限位冲和弹壳外模具共同组成冲压弹壳的上模，加工冲头对弹壳底部圆壳进行冲压平底，实现弹壳底部的成形。弹壳外模具与弹壳之间装配间隙为0，即外模具从外部抱死弹壳。如图1所示限位冲与弹壳之间的装配间隙为0.03～0.05 mm，以便于弹壳在冲压过程中弹壳内的金属流动。由于弹壳的制造过程是通过对材料多次冲压引伸加工制成，因此弹壳内部直径参数依据引伸的次数和状态呈阶梯状变化分布(见图2和图3)。

采用有限元ANSYS分析软件对弹壳的冲压模型进行仿真(见图4)，网格划分最小尺寸密度为0.05 mm，网格划分后的弹壳的模型如图5所示。在设置模型的约束时，将弹壳内冲头和外模具设置为刚体接触，约束方向是全自由度约束。加载载荷分为2个子步模拟动态加载，加载力大小为2.0×104kN，施加方向为Z轴负方向，行程2.8 mm，子步时间间隔1 s。

图1 平底前冲头、弹壳、限位冲和外模之间装配关系图

图2 冲压前弹壳尺寸参数

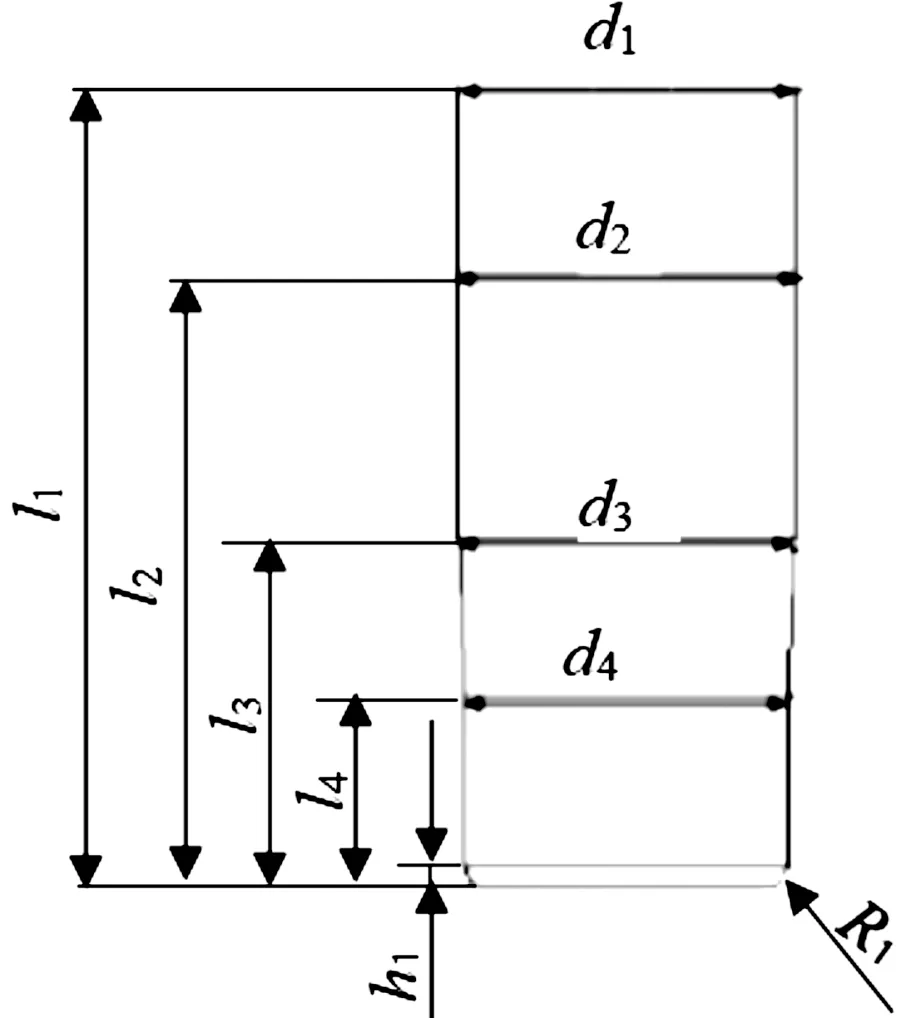
图3 弹壳内部限位冲头参数

表1 弹壳用H68铜材参数

图4 子弹壳有限元分析三维模型

图5 弹壳网格划分

依据图6和图7的分析结果，弹壳冲压过程中的最大应力位于弹壳外部与外模具的拐角处，最大应力为365 MPa，由于减薄和回弹的影响，仿真完成后弹壳变形面与外模具未完全接触(见图6)。主要影响因素为外模具圆角半径r及外模具与弹壳内部限位模的位置高度差h引起，外模具圆角半径直接影响弹壳平底时的回弹量，为避免上述误差需设置外模具与弹壳内部限位模的位置高度差，以抵消冲压回弹的影响，基于以上问题提出以下弹壳平底冲压优化模型和方法，以优化倒圆角和冲压模的设计参数，提高弹壳底部平底的精度。

图6 弹壳1/4模型变形云图

图7 弹壳的等效应变图

2 弹壳平底参数优化模型

弹壳在平底加工过程中，影响弹壳成形的参数主要有弹壳的冲压速度、动摩擦系数和弹壳材料的应力等因素，由于金属的流动性，其在冲压变形过程中变形部分会产生减薄，从而引起弹壳冲压后弹壳部分质量和体积的变化。依据弹壳的体积不变原理构建弹壳平底工序的坐标系，如图8(a)和(b)所示，以弹壳的径向为X轴，轴向为Z轴，以右手定则确定Y轴方向，原点O位于三坐标轴交点。图8(a)中点A表示弹壳冲压前底部变形的边缘点；图8(b)中点B与A点之间的圆弧为弹壳冲压变形后底部的圆弧形状，该圆弧的半径可近似等于弹壳外模具的圆角半径r，点C与点B之间的圆弧为平底后壳体变形后形成的圆角，可通过弹壳的工艺设计参数获得。图9表示弹壳内外模的参数关系，其中，点A＇对应图8中的点A，点B＇对应图8中的点B，内冲头作用是在弹壳内部顶死弹壳以减小弹壳在冲压过程中内部的变形，h表示限位模与外模具装配时的高度差，其作用是减小弹壳平底时金属的回弹。此外，为实现最佳的冲压效果，可假设弹壳在冲压前后的体积变化量最小时，即：金属在A点处沿着Z轴的负方向的流动量最小时，弹壳平底效果最好。因此可得到如下目标函数：

min{V(r′,h)-V′(r,h)}

(1)

其中：V(r′,h)为弹壳平底前的体积函数;r为外模具圆角半径；r′为弹壳的外径；h为外模具与限位模之间的高度差；V′(r,h)弹壳冲压完成后的体积函数。

图8 弹壳平底模型

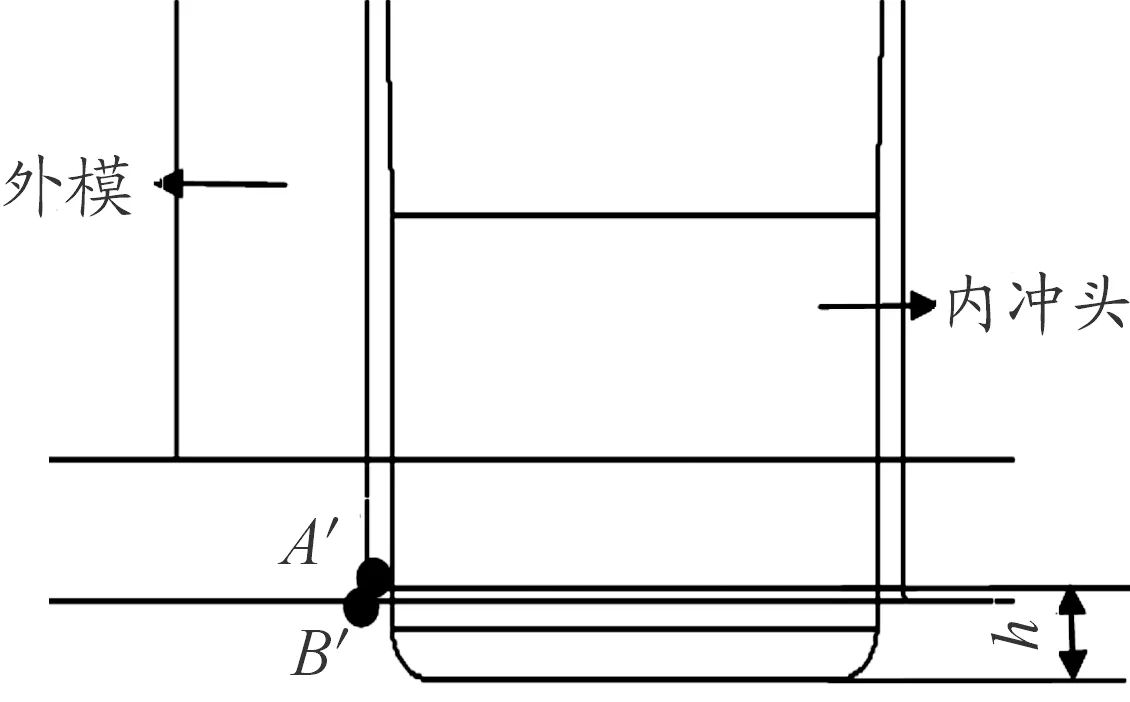
图9 弹壳内外模的参数关系

依据图8(a)中的坐标系点A与点B之间形状为圆环柱体，其高度为体积函数的参数h(即：限位模与外模具之间的高度差)，因此冲压前弹壳的体积函数可表示为弹壳从点A到点B之间圆环柱的体积与点B沿Z轴正方向半球体的体积之和，其表达式为

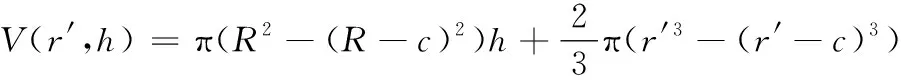
(2)

其中：c是弹壳冲压前的壁厚，R是弹壳冲压前圆环体的半径。

由于上式中弹壳冲压前圆环体的半径值与弹壳外径r＇相等。因此，式(2)也可表示为

(3)

依据图8(b)所示，点A与点B之间的弧，点B与点C之间的弧可通过样弹的弹壳参数获得，在XOZ坐标系中，为了计算点A与点B之间以及点B与点C之间的体积，将点A到点C的弧展成两段分段的直线段，其截面积可简化计算为

Ab=(lab+lbc)c′

(4)

其中:lab是点A与点B之间弧长；lbc是点B与C之间的弧长；c＇是平底后弹壳底部的厚度。

由弧长的计算公式可得

lab=αr

(5)

lbc=βrb

(6)

其中：α为点A与点B之间弧对应的圆心角，可由样弹弹壳标准图查得；β为点B与点C之间弧对应的圆心角，同理可由样弹弹壳标准查得。

弹壳在拉伸后的体积可看作截面积Ab绕轴Z回转一周后与点C到Z轴之间圆柱体的体积之和，将式(5)与式(6)代入式(4)后，可得弹壳平底后的体积计算表达式为

(7)

其中，h/2c＇为弹壳平底减薄后的理论值；d＇为弹壳减薄后的底部直径。

依据弹壳设计误差阈值，约束条件可定义为

(8)

将式(3)-式(7)代入式(1)且与式(8)联立可建立弹壳平底参数优化模型为

(9)

代入设计参数进行求解，可得最优设计参数外模具圆半径r为0.1 mm，限位模与外模具之间的高度差h为0.5 mm时弹壳的反弹最小，弹壳能够达到最优的平底效果。

3 优化结果仿真验证

有限元模型参数采用表1参数，采用图5的参数设置方式，将有限元模型的倒圆半径r设置为0.1 mm，限位模与外模具之间的高度差h设置为0.5 mm，其余参数与第1小节参数设置相同，代入有限元模型求解，得到弹壳平底模型的有限元变形和等效应力图。

由图10、图11和图12仿真结果说明，在弹壳参数优化后弹壳底部平底效果达到了理想值，弹壳压缩面与内外模面紧密贴合，应力回弹较小，误差在0.001 mm以内，满足了弹壳平底工艺要求。

图10 优化后弹壳底部的变形图

图12 优化后弹壳平底工艺的等效应力图

4 结论

基于弹壳冲压过程中的体积不变原理，建立了弹壳平底冲压优化数学模型，优化求解了弹壳冲压模具的设计参数，通过该优化模型得到外模具圆角半径r为0.1 mm，限位模与外模具之间的高度差h为0.1 mm时，弹壳的平底效果最好。采用有限元分析软件得到的模拟分析结果验证了优化模型的准确性。弹壳平底冲压优化模型提高了弹壳冲压模具的设计效率，有效降低了弹壳冲压过程中模具和冲头材料的损耗。