基于滑模观测器的鲁棒变结构一体化导引控制律
2017-03-09杨靖王旭刚王中原常思江
杨靖, 王旭刚, 王中原, 常思江
(南京理工大学 能源与动力工程学院, 江苏 南京 210094)
基于滑模观测器的鲁棒变结构一体化导引控制律
杨靖, 王旭刚, 王中原, 常思江
(南京理工大学 能源与动力工程学院, 江苏 南京 210094)
针对测量信息受限的远程制导炮弹精确末制导问题,提出了一种基于滑模观测器的变结构鲁棒控制方法,依据Lyapunov稳定性理论证明了其有效性;应用所提出的方法设计了一种两回路一体化导引控制律。考虑弹体短周期动力学特性及舵回路1阶动力学滞后,视气动参数偏差与目标机动为有界不确定项,建立了两回路导引控制一体化设计模型。外环以零化视线角速率为目标,生成虚拟俯仰角速率指令;内环确保实际俯仰角速率跟踪到外环给出的指令。仿真结果表明,在测量信息受限、存在气动参数偏差和目标机动不确定的条件下,所提出的导引控制一体化设计方法具有高命中精度和良好的过载特性。
兵器科学与技术; 远程制导炮弹; 导引控制一体化; 滑模观测器; 变结构控制
0 引言
间瞄火炮武器系统在战场中反应迅速,能够提供强大且持续的火力支援,是未来部队联合作战的重要组成单元。然而,适用于间瞄火炮的传统炮弹存在射程较近、精度不高的弊端。因此,远程制导炮弹的研制受到各国重视[1-2]。为实现精确打击,关键之一在于设计适配的末端导引控制律。
受火炮发射平台的限制,远程制导炮弹的翼及舵面面积与相近口径的导弹相比较小,控制能力与机动能力有限。同时,由于火炮发射的高过载,限制了惯性导航等测量装置在远程制导炮弹上的使用。因而,对于远程制导炮弹而言,导引控制律的设计,需要在可用测量信息受限条件下,确保命中精度的同时使得需用过载尽可能小。
导引控制系统一体化设计,不同于传统的频谱分离假设下的导引与控制系统设计的思路,因其充分考了虑弹体动力学特性对导引律性能的影响,具有更好的过载特性与末端性能,近年来成为导引控制系统设计领域的研究热点之一。文献中广泛使用的“导引控制一体化设计”的概念具有两种不同的含义:其一,将导引控制系统的作为一个整体,直接生成全状态反馈的舵控指令,称为单回路的导引控制一体化设计[3-5];其二,采用两回路的拓扑结构,外环导引律的设计考虑内环迎角滞后的现象,产生虚拟的俯仰角速率指令,内环控制律用来确保弹体实际俯仰角速率跟踪到外环给出的指令[6-8]。与单回路结构相比,两回路的导引控制一体化结构可以降低系统的相对度,同时因俯仰角速率实际可测量便于工程实现。因此,本文采用两回路的一体化导引控制设计结构。
目前用于研究导引控制一体化设计的方法主要包括最优控制、反馈线性化、反演设计和变结构控制等[9]。其中,变结构控制与其他方法相比具有对内部或外界的匹配扰动不敏感、控制精度高、有限时间收敛且算法简单易于实现等特点,应用较为广泛。Shima等[4]以零控脱靶量(ZEM)为滑模面,基于传统变结构控制理论,设计了一种一体化导引控制律,但是ZEM的计算依赖于剩余飞行时间等信息,工程实践中难以准确估计得到;Shtessel等[8]以零化视线角速率为目标,设计了一种两回路一体化导引控制律,但其外环采用传统的滑模面,仅能确保视线角速率是指数收敛的,而非有限时间内收敛到0,且其内环预设收敛滑模面存在奇异性;王洪强等[10]提出了一种非奇异终端滑模末制导律,但未考虑弹体的动力学特性;董飞垚等[11]针对拦截弹,综合考虑导引控制系统的耦合关系,提出了一种高阶滑模导引控制一体化设计方法,但其需要抵消的非线性项中包含较多的状态信息,对于远程制导炮弹无法获得; 齐辉等[12]考虑了弹体动态特性,结合反演方法与滑模方法提出了一种一体化制导控制策略,该方法对未建模动态及目标不确定性具有较强的鲁棒性,但依赖于攻角等弹体状态信息,对于远程制导炮弹难以测得。
基于上述考虑,本文针对测量信息受限的远程制导炮弹精确末制导问题,提出了一种基于滑模观测器的非奇异变结构鲁棒控制方法,依据Lyapunov稳定性理论证明了其有限时间收敛特性,应用所提出的方法设计了一种两回路一体化导引控制律。实现了存在弹体气动参数偏差和目标机动不确定性的精确末制导。
1 问题描述
为了研究制导炮弹精确末制导问题,需要建立简单合理的导引控制系统设计模型。远程制导炮弹通常为轴对称外形,具有滚转稳定系统,采用侧滑转弯机动模式。因而,可实现三通道解耦,仅考虑纵向平面内的运动。
1.1 平面内弹目相对运动模型
纵向平面内的弹目相对运动关系如图1所示:Oxy为地面参考惯性坐标系,R为弹目相对距离,λ为弹目视线(LOS)角;v、θ、a分别表示速度、弹道倾角和加速度;下标P、T分别表示炮弹、目标。
采用极坐标(R,λ),有弹目相对运动关系为
(1)
式中:
(2)
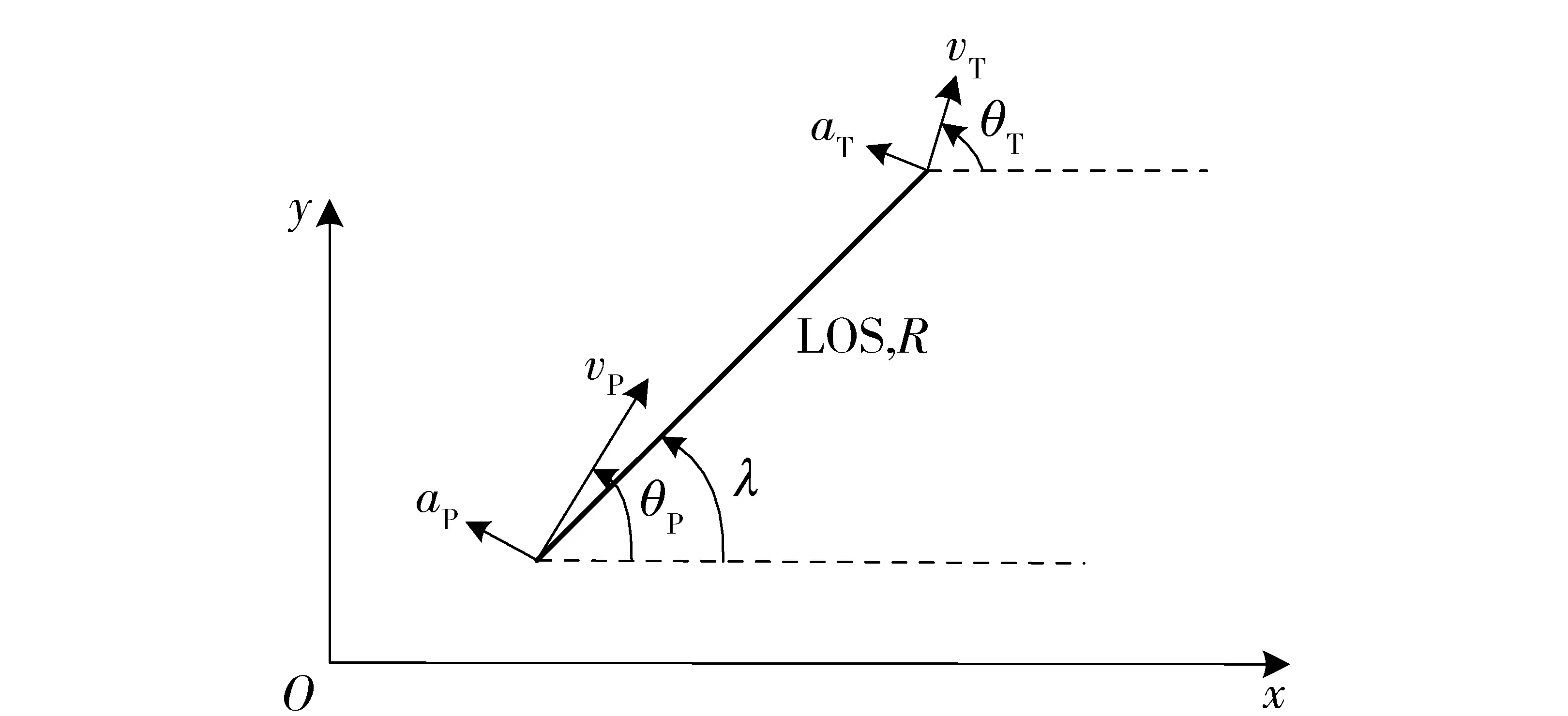
图1 平面内弹目相对运动关系Fig.1 Relative motion of projectile and target in plane
(3)
1.2 远程制导炮弹纵向动力学模型
将舵回路考虑为1阶动力学过程,远程制导炮弹纵向平面内的动力学模型为
(4)
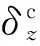
(5)
依据力学关系,法向加速度aP表示为
aP=Y/m.
(6)
1.3 两回路导引控制一体化设计模型
(7)
式中:tf为制导终止时间。
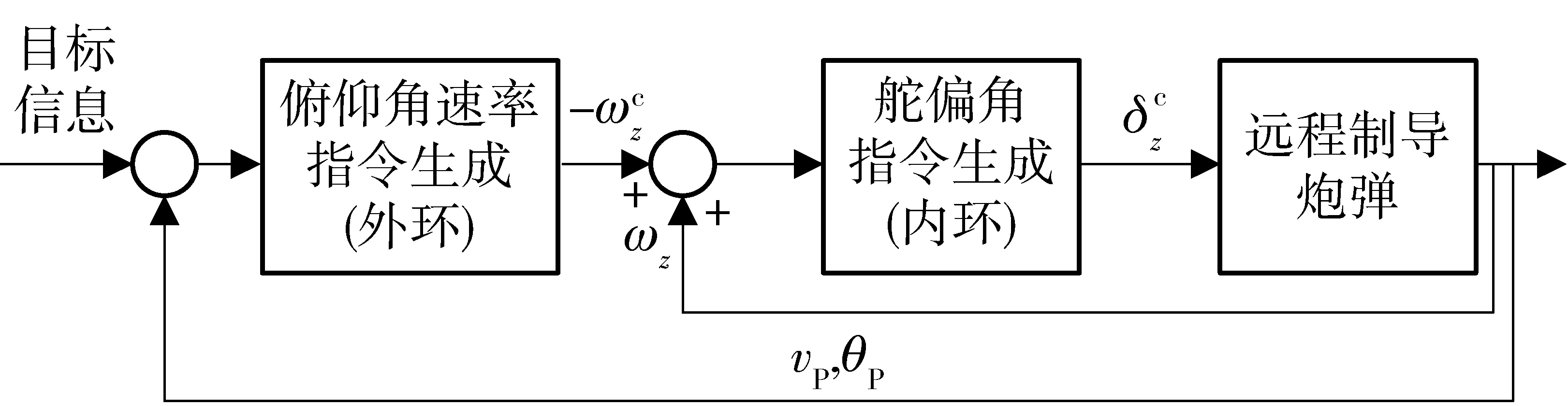
图2 两回路导引控制一体化结构框图Fig.2 Two-loop IGC diagram
对(6)式求导,综合(3)式~(5)式,整理得两回路导引控制一体化设计模型为:
1)外环动力学模型
(8)
2)内环动力学模型
(9)
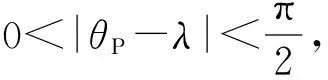
2 两回路鲁棒导引控制一体化设计
2.1 基于滑模观测器的鲁棒变结构控制方法
选取慢性心力衰竭合并2型糖尿病患者74例作为研究对象,将其随机分为替米沙坦组和雷米普利组,各37例,比较两组慢性心力衰竭治疗效果、空腹血糖水平、胰岛素水平及不良反应发生率。入院时,患者均符合美国心脏病协会制定的关于慢性心力衰竭的诊断标准,1999年WHO制定的关于2型糖尿病的诊断标准,空腹血清C肽平均指数为(2.61±0.21)nmol/L,排除免疫系统疾病者、血液系统疾病者、精神疾病者等,其中,替米沙坦组女12例,男25例,平均年龄(36.92±2.14)岁;雷米普利组女11例,男26例,平均年龄(37.16±2.09)岁。两组患者一般资料比较,差异无统计学意义(P>0.05)。
考虑如下一般形式的2阶动力学系统
(10)
式中:x1、x2为状态变量;σ为系统输出;u为控制输入;f为光滑函数,依赖于状态变量、时间t以及不确定因素Δ;b已知且有b>0. 假设仅x1可测量,期望设计控制律使输出σ在有限时间内收敛于0.
对σ求2阶导数,可得u-σ输入输出动力学模型为
(11)
可以看出其相对度为2. 为了使σ在有限时间收敛于0,需要建立2阶滑动模态[13]。因此,选取滑模变量为
(12)
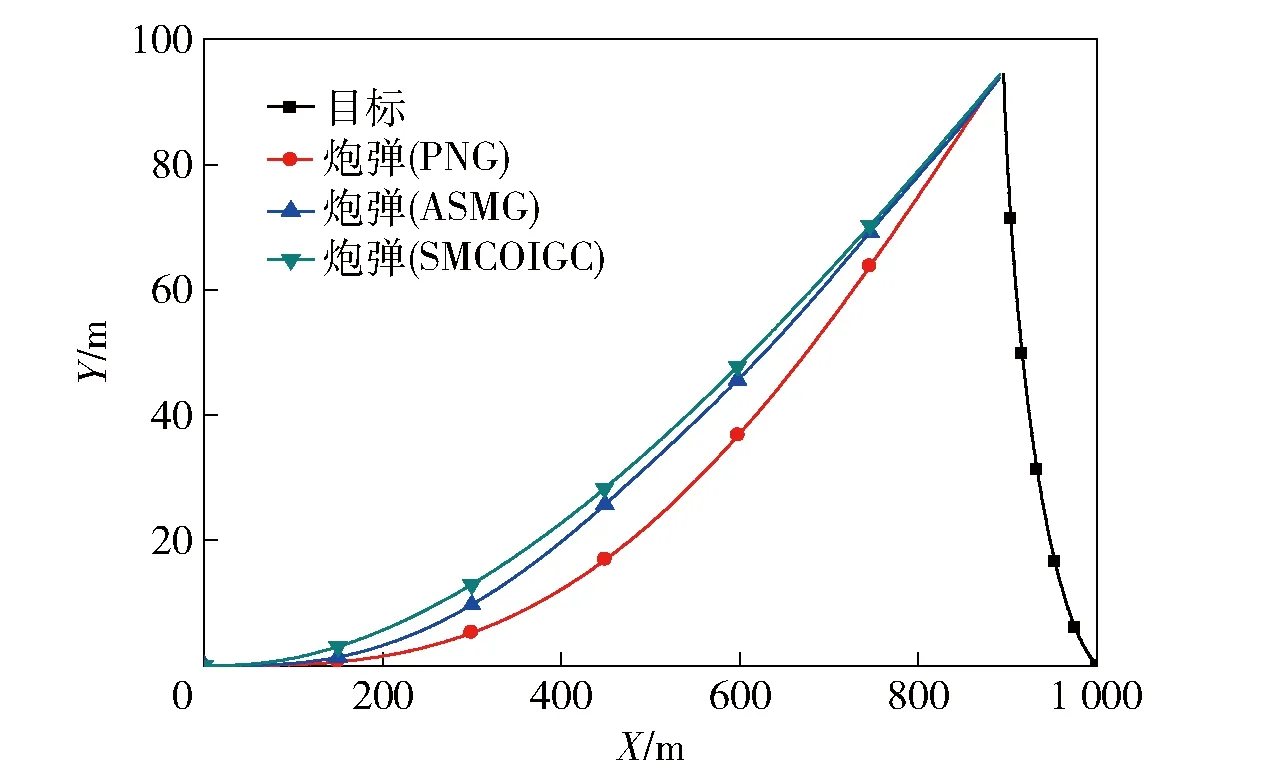
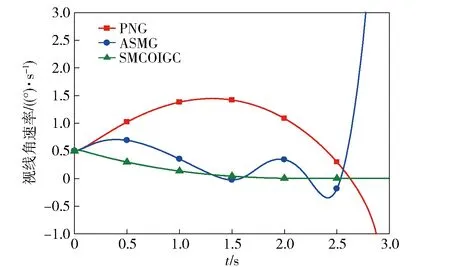
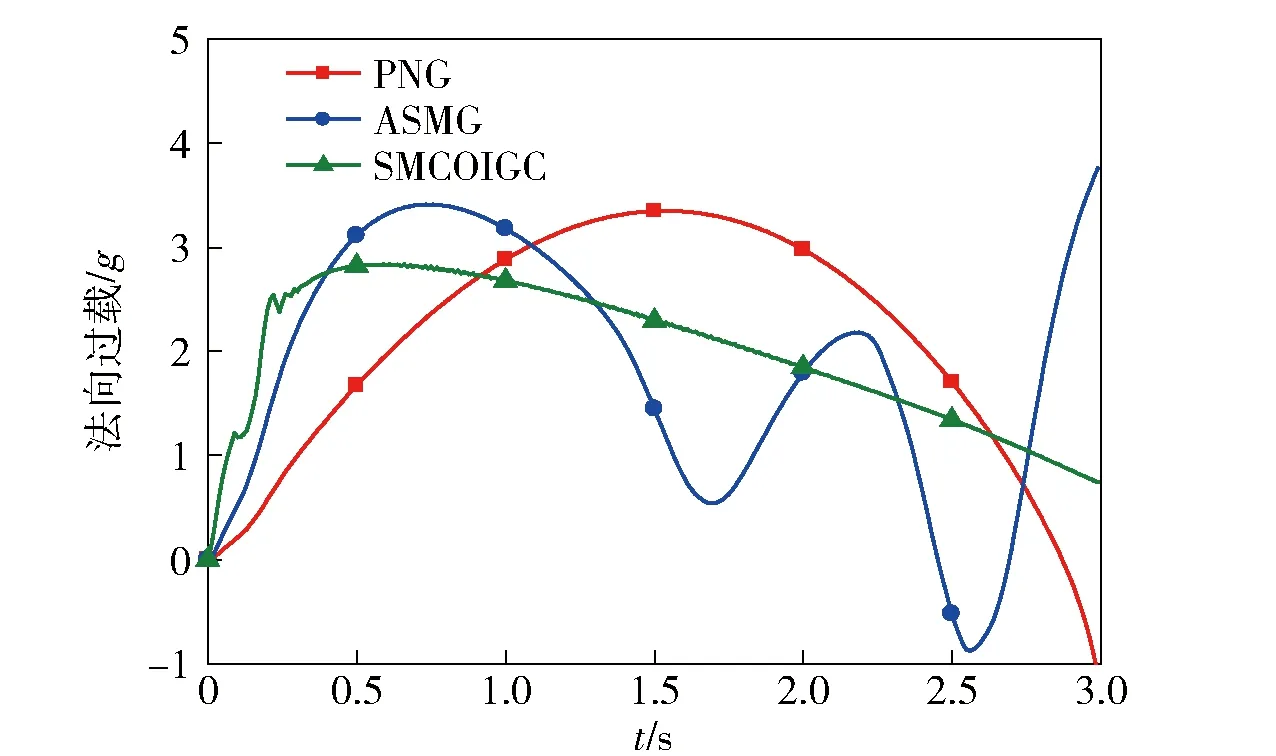
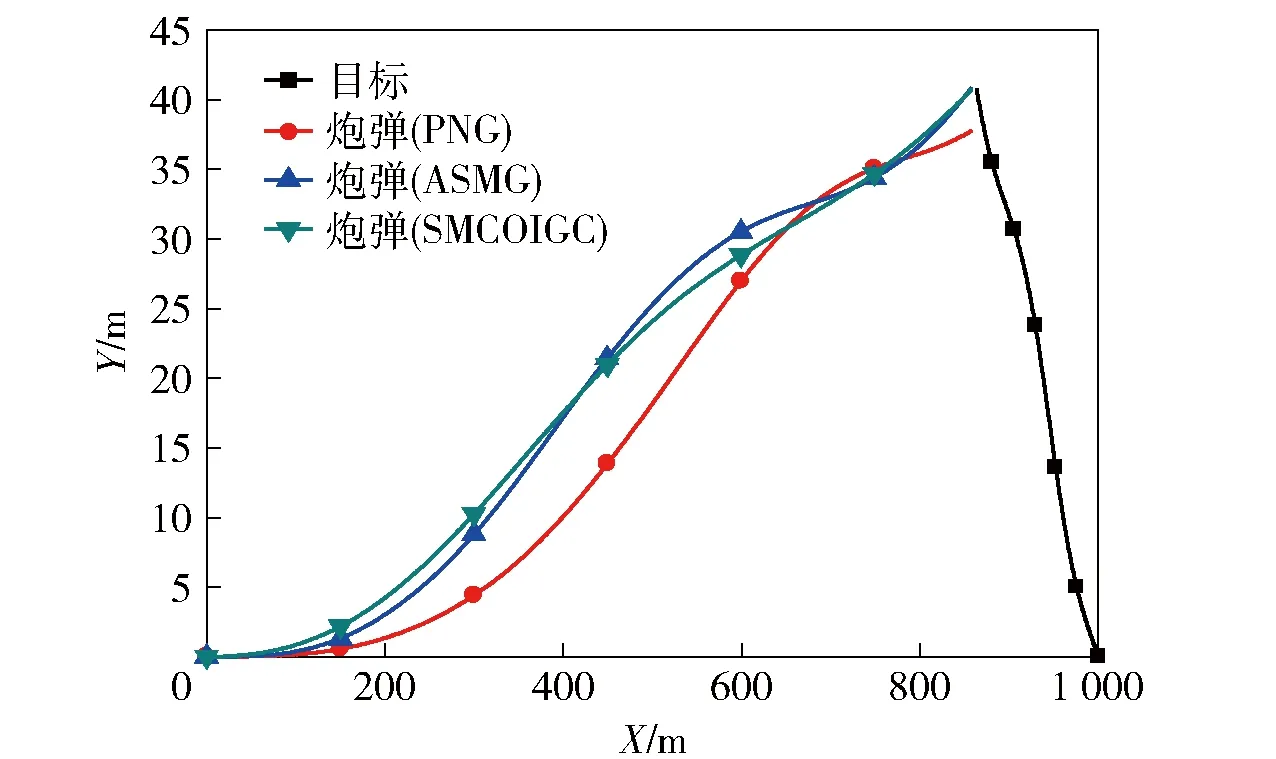
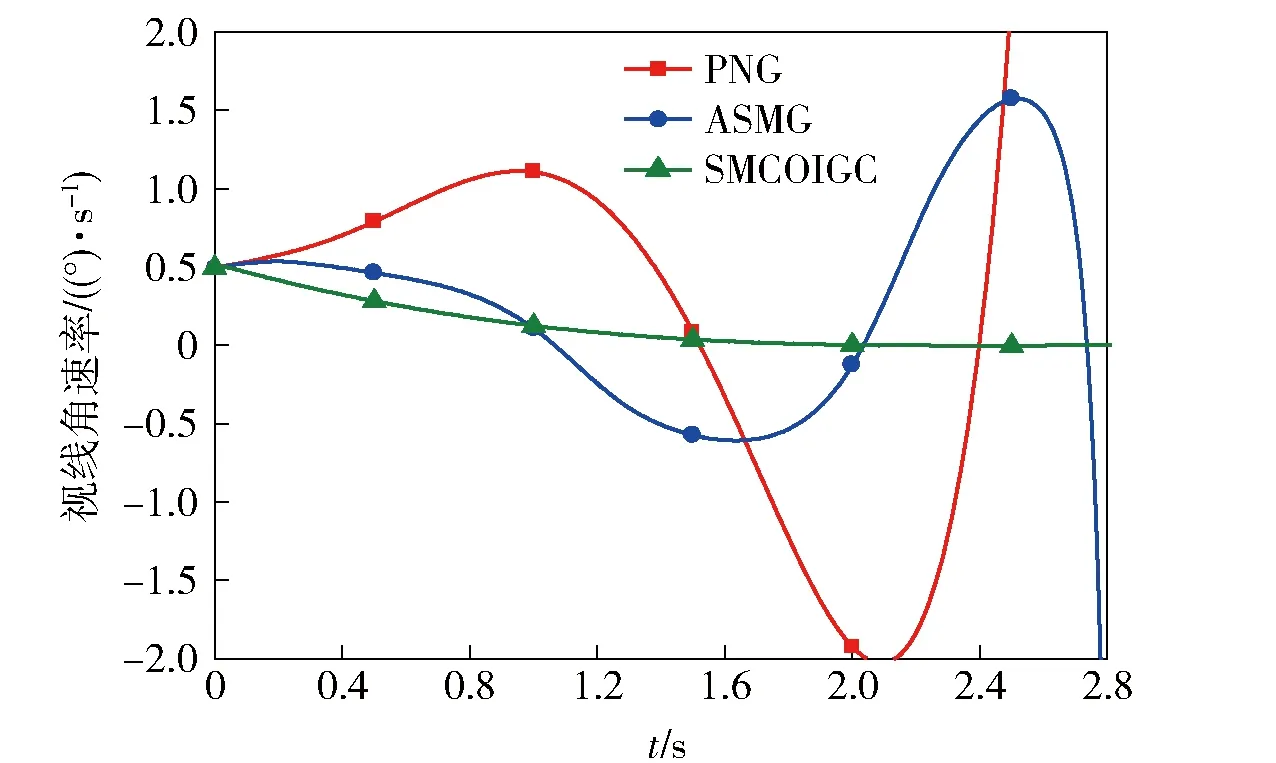
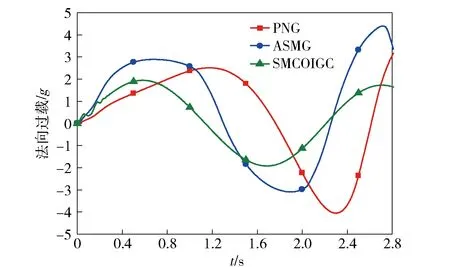
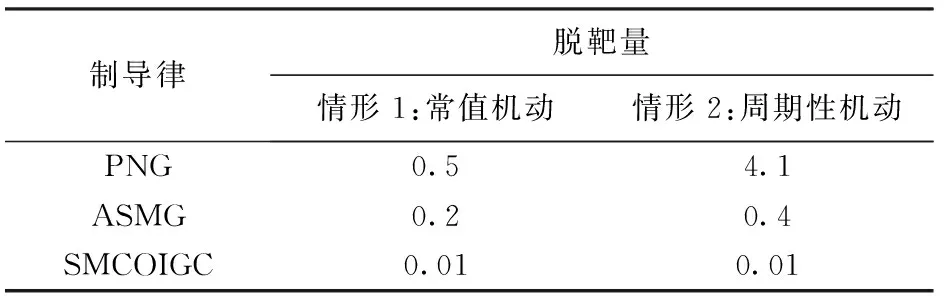
式中:c>0为常数;m、n>0为奇数且1 假设当t≥tr时,对于系统(10)式,(12)式定义的滑动模态(Σ=0)存在,即 (13) 式中:tr为到达时间。 积分(13)式,整理得 (14) (15) (16) 由于系统(11)式中包含不确定项,为使补偿系统具有良好的鲁棒性,通常所设计的控制律中需要包含高频切换项。大幅的高频切换控制可能会激发系统的高频未建模动态,进而引起系统失稳,所以减小切换项幅值降低震颤现象具有重要意义。为此,引入如下高阶滑模观测器[14]来精确估计f的值,以补偿不确定项的影响,从而减小切换项幅值。 (17) (18) 式中:c>0为常数;m、n>0为奇数且1 证明 取Lyapunov函数为 (19) 综上所述,控制律可确保Σ在有限时间内收敛于0,证毕。 2.2 外环鲁棒变结构导引律设计 (20) 结合(19)式,对(20)式求2阶导数,整理得 (21) 式中: 依据定理,为使σG在有限时间内收敛于0,选取如下滑模变量: (22) 式中:cG>0;1 (23) 依据定理,外环产生的俯仰角速率指令为 (24) 式中:参数含义如定理,wG1为采用形如(17)式的如下滑模观测器得到fG的估计值: (25) 2.3 内环鲁棒变结构控制律设计 通常俯仰角速率ωz可用速率陀螺测得,因此,取内环输出为跟踪误差,即 (26) 结合(19)式对(26)式求2阶导数,整理得 (27) 为使σC在有限时间内收敛于0,依据定理,取如下滑模变量: (28) 式中:1 (29) 依据定理,内环舵偏指令为 (30) 式中:参数含义如定理。wC1为采用形如(17)式的如下滑模观测器得到的fC的估计值: (31) 为了验证本文提出的基于滑模观测器的鲁棒变结构一体化导引控制律(SMCOIGC)的有效性与优越性,本节将该方法与以下两种制导律进行仿真对比分析: 方法1:比例导引律(PNG)[15], (32) 方法2:自适应滑模导引律(ASMG)[16], (33) 式中:取N2= 4;kG=21;ε=0.001. 3.1 仿真条件 目标质点运动模型假设如下: (34) 式中:目标速度大小vT恒定,取为50 m/s;时间常数τT取为0.1 s. 目标机动策略采用以下两种典型情形: 情形1:目标常值机动指令, (35) 情形2:目标周期性机动指令, (36) 末制导阶段,制导炮弹速度取为300 m/s. 在速度vP=300 m/s与飞行高度800 m的条件下,制导炮弹的动力系数如表1所示,并在此基础上摄动20%. 设制导炮弹舵回路时间常数τδ=0.02 s,最大舵偏角设为25°. 表1 远程制导炮弹参数 设制导炮弹与目标的初始相对距离为1 000 m,初始对准误差为5°. 3.2 用于PNG与ASMG的自动驾驶仪 考虑到弹体动力学特性,仿真PNG与ASMG时引入经典三回路自动驾驶仪[15],具体见图3所示。 图3 经典三回路自动驾驶仪Fig.3 Classic three-loop autopilot (37) 式中:KR、KI、KA、KDC为可调参数。 采用表1制导炮弹动力系数,设计控制律(37)式中的参数为KA=0.010 7,KI=13.981 4,KR=-0.750 3,KDC=1.312 6,经典三回路自动驾驶仪的加速度单位阶跃响应如图4所示。 图4 经典三回路自动驾驶仪单位阶跃响应Fig.4 Step response of classic three-loop autopilot 3.3 3种方法的制导性能对比 如前所述,(22)式~(25)式,(28)式~(31)式共同构成了基于滑模观测器的鲁棒变结构一体化导引控制律。从算法复杂度讲,包含4组观测器,运算量为12个1阶常微分方程初值问题的数值积分。就目前的计算机水平而言,与另外两种方法的运算时间的差别可忽略不计。 在两种典型目标机动情形的仿真中,3种制导方法的参数设定保持一致。 3.3.1 情形1:目标常值机动 目标常值机动时,3种制导方法的仿真结果如图5~图7所示。图5描述了初始视线坐标系下制导炮弹与目标的运动轨迹。从中可以看出,3种制导方法脱靶量都很小,表2列出了各方法对应的脱靶量。图6为弹目接近过程中,视线角速率的变化情况。由图6可见,采用PNG与ASMG的制导末端,视线角速率都存在发散现象,而采用本文提出的SMCOIGC可确保视线角速率在有限时间内收敛于0. 图7展示了在不同制导方法下,制导炮弹的法向过载曲线。由图7可以看出:PNG和ASMG需要过载相当,SMCOIGC与前二者相比,需用过载较小;制导末端,PNG和ASMG出现过载发散现象,而SMCOIGC末端过载收敛;制导初始段,SMCOIGC的过载有小幅抖动,是由高阶滑模观测器的短暂收敛过程引起的。 图5 情形1:初始视线坐标系下的弹目运动轨迹Fig.5 Case 1: Projectile and target trajectory with respect to initial line-of-sight coordinates 图6 情形1:视线角速率变化比较Fig.6 Case 1: Line-of-sight rate profile 图7 情形1:法向过载变化比较Fig.7 Case 1: Acceleration profile 3.3.2 情形2:目标周期性机动 目标周期性机动时,3种制导方法的仿真结果如图8~图10所示。图8描述了初始视线坐标系下制导炮弹与目标的运动轨迹。从中可以看出,ASMG与SMCOIGC仍可命中目标,而PNG脱靶量较大,表2列出了各方对应的脱靶量。图9为弹目接近过程中,视线角速率的变化情况。与情形1类似,采用PNG与ASMG的制导末端,视线角速率都存在发散现象,而采用本文提出的SMCOIGC可确保视线角速率在有限时间内收敛于0. 图10展示了在不同制导方法下,制导炮弹的法向过载曲线。从中可以看出:PNG和ASMG需要过载相当,SMCOIGC与前二者相比,需用过载较小;制导初始段SMCOIGC的过载小幅抖动是由高阶滑模观测器的收敛过程引起的,之后低频大幅震荡是由于目标的周期性机动引起的,因为零化视线角速率等价于制导炮弹与目标在垂直于视线方向上的过载一致。 图8 情形2:初始视线坐标系下的弹目运动轨迹Fig.8 Case 2: Projectile and target trajectory with respect to initial line-of-sight coordinates 图9 情形2:视线角速率变化比较Fig.9 Case 2: Line-of-sight rate profile 图10 情形2:法向过载变化比较Fig.10 Case 2: Acceleration profile 制导律脱靶量情形1:常值机动情形2:周期性机动PNG0.54.1ASMG0.20.4SMCOIGC0.010.01 本文针对远程制导炮弹打击地面或海上机动目标的末端制导过程,考虑测量信息受限、弹体气动参数的不确定性以及目标未知有界的机动策略,提出了一种基于滑模观测器的鲁棒变结构两回路一体化导引控制律,依据Lyapunov稳定性理论证明了其有效性。仿真结果表明: 1)在测量信息受限、存在气动参数偏差和目标机动不确定的条件下,本文提出的导引控制一体化设计方法具有高命中精度和更好的过载特性。 2)在末制导初始阶段,高阶滑模观测器的快速收敛过程会引起制导炮弹过载的小幅抖动现象。在实际应用中需要综合考虑导引头的测量性能。 References) [1] 杨荣军, 石运国. 制导炮弹离散自适应滑模控制器设计[J]. 弹道学报, 2014, 26(2): 34-38. YANG Rong-jun, SHI Yun-guo. Design of discrete-time adaptive sliding mode controller for guided projectiles[J]. Journal of Ballistics, 2014, 26(2): 34-38. (in Chinese) [2] Strub G, Basset M. Skid-to-turn autopilot design and validation for an experimental guided projectile prototype[C]∥AIAA Guidance, Navigation, and Control Conference. San Diego, California, US: AIAA, 2016. [3] Levy M, Shima T, Gutman S. Linear quadratic integrated versus seperrated autopilot-guidance design[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(6): 1722-1730. [4] Shima T, Idan M, Golan O. Sliding-mode control for integrated missile autopilot guidance[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2): 250-260. [5] Park G, Kim H, Tahk J. Time-delay control for integrated missile guidance and control[J]. International Journal of Aeronautical and Space Science, 2011, 12(3): 260-265. [6] Padhi R, Chawla C, Das G. Partial integrated guidance and control of interceptors for high-Speed ballistic targets[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(1): 149-163 [7] Wang X, Wang J. Partial integrated guidance and control with impact angle constraints[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(5): 925-936. [8] Shtessel Y, Tournes C. Integrated higher-order sliding mode guidance and autopilot for dual-control missiles[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(1): 79-94. [9] 薛文超, 黄朝东, 黄一. 飞行制导控制一体化设计方法综述[J]. 控制理论与应用, 2013, 30(12): 1511-1520. XUE Wen-chang, HUANG Chao-dong, HUANG Yi. Design methods for the integrated guidance and control system[J]. Control Theory & Applications, 2013, 30(12):1511-1520. (in Chinese) [10] 王洪强, 方洋旺, 伍友利. 基于非奇异Terminal滑模的导弹末制导律研究[J]. 系统工程与电子技术, 2009, 31(6): 1391-1395. WANG Hong-qiang, FANG Yang-wang, WU You-li. Research on terminal guidance law of missiles based on nonsingular terminal sliding mode[J]. Systems Engineering and Electronics, 2009, 31(6): 1391-1395. (in Chinese) [11] 董飞垚, 雷虎民, 周池军, 等. 导弹鲁棒高阶滑模制导控制一体化研究[J]. 航空学报, 2013, 34(9): 2212-2218. DONG Fei-yao, LEI Hu-min, ZHOU Chi-jun, et al. Research of integrated robust high order sliding mode guidance and control for missiles[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2212-2218. (in Chinese) [12] 齐辉, 张泽, 韩鹏鑫, 等. 基于反演滑模控制的导弹制导控制一体化设计[J]. 系统工程与电子技术, 2016, 38(3): 618-623. QI Hui, ZHANG Ze, HAN Peng-xin, et al. Integrated design of missile guidance and control based on back-stepping and sliding mode control [J]. Systems Engineering and Electronics, 2016,38(3): 618-623. (in Chinese) [13] Levant A. Sliding order and sliding accuracy in sliding mode control[J]. International Journal of Control, 1993, 58(6): 1247-1263. [14] Levant A. High-order sliding mode, differentiation and output-feedback control[J]. International Journal of Control, 2003, 76(9): 924-941. [15] Zarchan P. Tactical and strategic missile guidance[M]. New York: AIAA, 2012. [16] Zhou D, Mu C, Xu W. Adaptive sliding-mode guidance of a homing missile[J]. Journal of Guidance, Control, and Dyna-mics, 1999, 22(4): 589-594. Sliding-mode-observer-based Robust Variable Structure Control for Integrated Autopilot-guidance YANG Jing, WANG Xu-gang, WANG Zhong-yuan, CHANG Si-jiang (School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China) A novel sliding-mode-observer-based variable structure controller is proposed and proved by Lyapunov’s theorem for integrated guidance and control(IGC) synthesis for extended range guided projectiles (ERGP) in order to realize hit-to-kill interception with limited measurement. Accounting for the short-period dynamics of the ERGPs and first-order lag of the canard servo, the two-loop IGC model is formulated in the presence of the discrepancies from aerodynamic parameters and target maneuver. The outer-loop of the IGC generates the commanded pitch rate to regulate the line-of-sight (LOS) rate to zero in finite time; the inner-loop is designed to track the outer-loop command. Simulation results show the effectiveness of the proposed controller and that the acceleration requirement is reduced. ordnance science and technology; extended range guided projectile; integrated guidance and control; sliding mode observer; variable structure control 2016-07-08 国家自然科学基金项目(11402117) 杨靖(1988—),男,博士研究生。E-mail: jingyangnust@163.com 王旭刚(1979—),男,副研究员,博士生导师。E-mail:wxgnets@163.com TJ413+.6 A 1000-1093(2017)02-0246-08 10.3969/j.issn.1000-1093.2017.02.006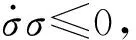
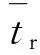
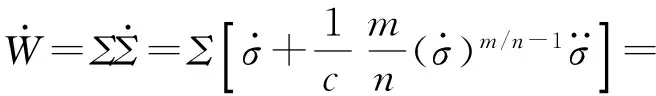

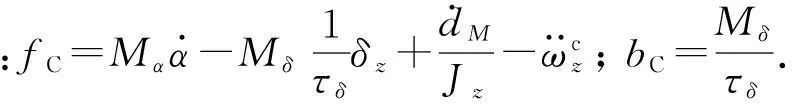
3 仿真分析
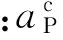

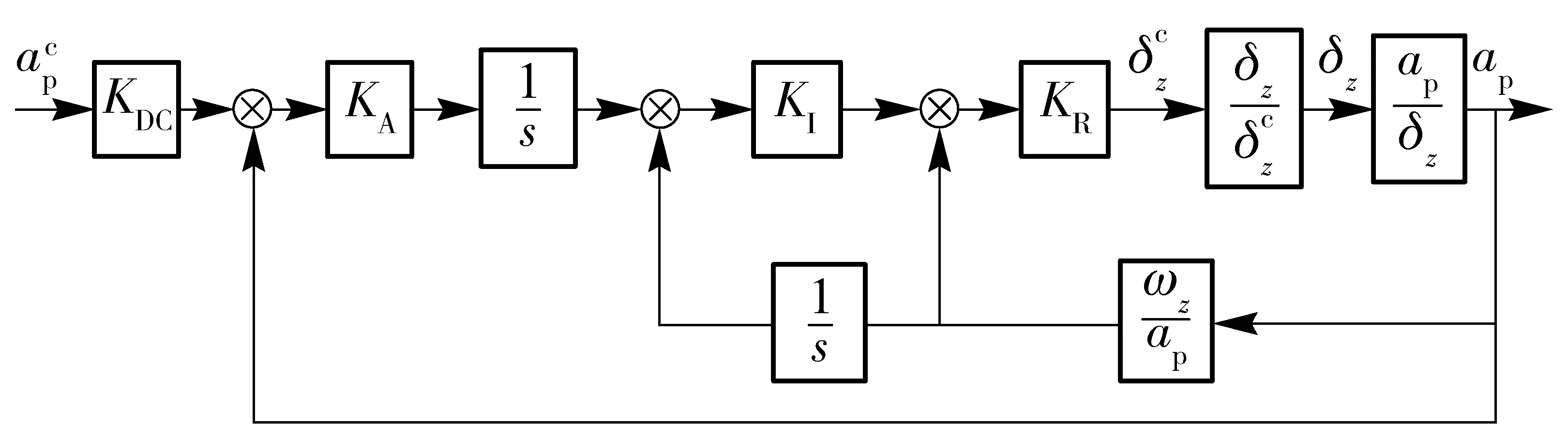
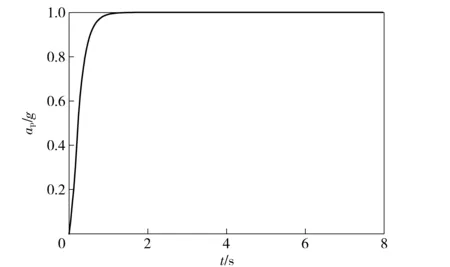
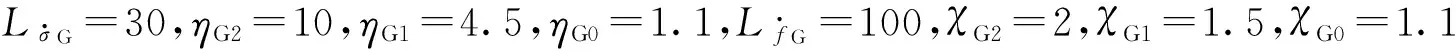
4 结论
