时滞广告量-购物水平模型稳定性和Hopf分支研究

王晓红，翟延慧，郭 伟

(1. 天津工业大学 理学院，天津 300387；2. 天津科技大学 生物工程学院，天津 300457)

时滞广告量-购物水平模型稳定性和Hopf分支研究

王晓红1，翟延慧1，郭 伟2

(1. 天津工业大学 理学院，天津 300387；2. 天津科技大学 生物工程学院，天津 300457)

讨论了具有时滞的广告量-购物水平模型的稳定性和Hopf分支.应用Hopf分支理论和泛函微分方程方法研究了该模型的线性稳定性和局部Hopf分支.把时滞变量当做分支参数，利用规范型理论和中心流形定理给出了确定分支方向及分支周期解稳定性的计算公式，且通过数值模拟验证结论的有效性.

广告量-购物水平模型；时滞；Hopf分支；稳定性

1 模型的建立

许多学者致力于广告量-购物水平模型的研究.在文献[1]中王树禾构建了传统的广告量-购物水平模型，文献[2-3]对一些经济模型的平衡点及稳定性进行了研究.然而，仅有少数对具有时滞的广告量-购物水平模型进行分析.首先引入传统的广告量-购物水平模型.

D·(t)=α(X0-x(t))+βy(t)(Y0-y(t)),

y·=γ(X0-x(t))

(1)

其中:x(t)表示t时刻的购物水平，y(t)表示t时刻的广告量.X0是最大购物水平，Y0是最大广告量.α,β,γ是常数.考虑到实际生活中，广告的效果受到社会、经济、文化、时空、地域等多种因素和条件的制约，并且消费者的反应程度是很不一致的，所以广告效果的获得具有时间推移性，即通常所说的时滞τ.商家从获得消费者购买信息到调整广告量需要一定的时间，也就是广告量的调整滞后于消费者的购买.因此，本文对模型(1)引入时滞，得到具有时滞的一类广告量-购物水平模型如下：

x·(t)=α(X0-x(t))+βy(t)(Y0-y(t)),

y·=γ(X0-x(t-τ))

(2)

2 稳定性和局部Hopf分支分析

根据模型的实际意义，这里仅对模型(2)唯一的正平衡点E=(X0,Y0),讨论其Hopf分支及稳定性问题.

令u1(t)=x(t)-X0，u2(t)=y(t)-Y0，将系统(1)在平衡点E处线性化后得到线性系统如下：

u·1(t)=-αu1(t)-βY0u2(t),

u·2(t)=-γu1(t-τ)

(3)

系统(3)在平衡点E处特征方程为

λ2+αλ-βY0γe-λτ=0

(4)

为了研究系统的平衡点E的稳定性和分支，我们只需要讨论特征方程(4)的根的分布即可，若方程(4)的所有根都有负实部则平衡点E稳定，若方程有一个根含有正实部则平衡点E不稳定.首先考虑单时滞τ=0的情况，此时特征方程(4)为：

λ2+αλ-βY0γ=0

(5)

很容易得出当且仅当(H1)α>0,βγ<0成立，特征方程的所有根都有负实部，因此平衡点E局部渐近稳定.接下来，观察随着时滞τ值的增大，特征方程(5)某些特征根的实部是否会增加至零，甚至变为正的.

当τ>0，假设λ=iω(ω>0)是特征方程(4)的一个解，当且仅当ω满足

-ω2+iωα-βY0γ(cosωτ-isinωτ)=0

分离实部和虚部，得到

-ω2=βY0γcosωτ

-αω=βY0γsinωτ

(6)

令A=βY0γ,v=ω2从而有v2+α2-A0=0等式有一个正实根v=-α2+α4+4A22，因此可以得到

τk=1ω[arccos-ω2A+2kπ],k=0,1,2,…. .

为了确定τk是否是分支值，我们需要验证如下横截条件是否成立.

引理1 若条件(H1)成立，横截条件Re(dλ-1dτ)>0成立.

证明：特征方程(4)对τ求导得出：

dλdτ=-λAe-λτ2λ+α+τAe-λτ,

显然我们可以得出Re(dλdτ)-1>0，证毕.根据文献[4]中Hopf分支存在定理，可得到下列结论.

引理2对方程(5)，如果(H1)成立，当τ∈[0,τ0)时，正平衡点E是局部渐近稳定的，且在τ=τk处正平衡点产生Hopf分支.

3 Hopf分支方向和周期解的稳定性

上一节中论述了Hopf分支产生的条件，本节将通过文献[5-6]的规范性理论和中心流行定理研究当Hopf分支理论的条件得到满足时，给出关于确定Hopf分支方向和分支周期解稳定性的计算公式，同时提供一种研究周期解存在性和稳定性的方法.

这里τ=τ0+μ，μ∈R，t=sτ，ui(t)=ui(tτ),i=1,2,为了记号方便，仍用ui(t)表示ui(t).系统(2)等价于抽象常微分方程

u·(t)=Lμ+F(μ,ut).

(7)

其中Lu(φ)=(τ0+μ)B1φ(0)+(τ0+μ)B2φ(-1),B1=-αβY0

00,B2=00

-γ0，且F(μ,φ)=(τ0+μ)-βφ2(0)

0.Lμ为C([-1,0],R3)→R3的有界线性算子且φ(θ)=(φ1(θ),φ2(θ))T∈C([-1,0],R3).

由Riesz表示定理知存在有界变差函数η(θ,μ):[-1,0]→R3×3使得

(8)

事实上我们选取

η(θ,μ)=B1δ(θ)+B2δ(θ+1)

(9)

这里δ(θ)是一个Delta函数.对φ∈C′([-1,0]R2)定义算子A和R如下：

A(μ)φ(θ)=d(φ(θ))dθ,θ∈[-1,0),

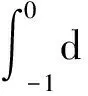
(10)

R(μ)φ(θ)=0,θ∈[-1,0),

F(μ,φ),θ=0.

(11)

则系统(7)可以写成如下形式：

u·t=A(μ)ut+R(μ)ut

(12)

令φ∈C′([0,1],(R2)*),与A(0)相应的共轭算子A*(0)被定义如下：

A*φ(s)=-dφ(s)ds,s∈(0,1],

(13)

对φ∈C′([-1,0],R2)和φ∈C′([0,1],(R2)*)，定义双线性形式：

(14)

假设q(θ)和q*(s)分别是A与A*的特征值iτ0和-iτ0ω相对应的特征向量.那么A(0)q(θ)=iτ0ωq(θ),A*(0)q*(s)=-iτ0ωq*(s)再根据A(0),A*(0)的定义，得到了A(0)q(θ)=dq(θ)dθ,A*(0)q*(s)=-dq*(s)ds则，q(θ)=q)0)eiτ0ω0θ，q*(s)=q*(0)eiτ0ω0s且

(15)

(16)

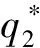
-α-βY0

-γe-tωτ00=1

q2=iω1

q2,-α-γe-iωτ0

-βY001

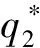
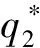
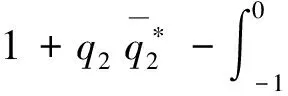
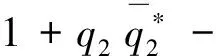
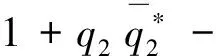
接下来，将利用Hassard[7]等人提出的计算方法在γ=0时，在中心流行C0上构建坐标，

z(t)=〈q*,ut〉,W(t,θ)=ut(θ)-2Re{z(t)q(θ)}

(17)

在中心流行C0上，我们有

W(t,θ)=W(z(t),z(t),θ)

(18)

这里(z,z,θ)=W20(θ)z22+W11(θ)zz+W02(θ)z-22+….

对中心流行C0，z和z分别是中心流行在q和q*方向上的局部坐标.我们仅考虑实解的情况，由μ=0，

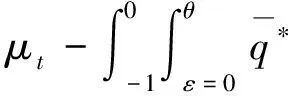
(19)

这里

f0(z,z)=fz2z22++fz2z-22+fzzzz+…,

(20)

将式(19)缩写为如下形式

z′(t)=iω0z+g(z,z),

(21)

其中

g(z,z)=g20z22+g11zz+g02z22+…,

(22)

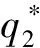
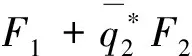
由式(17),(18)可得

W·=u·t-z·q-z·-q=A(0)W-2Req*(0)F0(z(t),z(t))q(θ),θ∈[-1,0),

A(0)W-2Req*(0)F0(z(t),z(t))q(θ)+F0,θ=0.

(23)

这里

H(z,z,θ)=H20(θ)z22+H11(θ)zz+H02(θ)z22+…

在中心流行C0中，将式(17)和(23)代入W·=Wzz·+Wzz·-，比较系数可得

H20(θ)=2iτ0ωW20(θ)-A(0)W20(θ),

H11(θ)=-A(θ)W11(θ)

由A的定义和(22)、(23)可以推导出如下方程：

W·20(θ)=2iωτ0W20(θ)-A(0)g20q(θ)+g20q(θ),

W·11(θ)=g11q(θ)+g11q(θ).

求解W20(θ)和W11(θ)得出

W20(θ)=ig20τ0ωq(0)e-iτ0ωθ+ig023τ0ωq(0)e-iτ0ωθ+E1e2iτ0ωθ

W11(θ)=-ig11τ0ωq(0)eiωτ0θ+ig11τ0ωq(0)eiωτ0θ+E2.

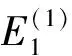
H(z,z,0)=-2Re[q*(0)F0q(θ)]=-g(z,z)q(θ)-g(z,z)q(0)

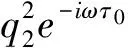
H11(0)=-g11q(0)-g11q(0)+τ0(-2βq2q2,0)T

(24)

由式(19)～(24)计算得到

E1=2iω+αβY0

γe-2iωτ02iω0-12 1

-γeiω0τ0iω0,

E2=-α-βY0

γe-iω0τ00-1-2βq2q2

0

接下来我们在临界值τ0处确定Hopf周期解的性质的几个重要值：

C1(0)=i2τ0ω(g20g11-2|g11|-13|g02|2)+g212

μ2=-Re{C1(0)}Re{λ′(τ0)}

β2=2Re{C1(0)}

T2=-Im{C1(0)}+μ2(Im{λ′(τ0)})ω

由文献[8]可知μ2决定了Hopf分支的方向，如果Re{C1(0)}<0(>0)，当τ=τ0时系统(2)在平衡点E处的分支周期解存在.若μ2>0(μ2<0)分支方向是前向(后向)的，即分支周期解存在于τ0的右侧(左侧)；若β2<0(β2>0)则在中心流行上的分支周期解是渐进稳定(不稳定)的.若T2>0(T2<0)则分支周期解的周期是递增(递减)的.特别的，当τ0时第一个或是最后一个分支值(τ1或τm)时，原系统的分支周期解的稳定性与它对应在中心流行上的周期解的稳定性相同.

4 数值模拟

我们需要通过适当的调整最大购物水平X0来保证广告量的投入在正常范围内，因此选择如下参数通过数值模拟验证上述研究结果的可靠性.令α=2.3,β=-1,γ=0.33且X0,Y0=2.5.从而平衡点E=(4,2.5).计算得，ω≈0.354 509,τ0≈3.999 52由以上结论可知：当τ=6.25>τ0时，平衡点是局部稳定的，如图1所示.当，系统产生Hopf分支，如图2所示.当时，平衡点是不稳定的，如图3所示.数值模拟展示了系统从稳定到不稳定的复杂的变换过程.

图1 τ=3<τ0的相图及时程图

图2 τ=3.999 52=τ0的相图及时程图

图3 τ=6.52>τ0的相图及时程图

5 结 语

本文的主要贡献在于以下几个方面：第一，修改了传统的广告量-购物水平模型，建立了具有双时滞的微分方程广告量-购物水平模型.第二，研究了系统(2)的稳定性和Hopf分支，此外，利用规范性理论和中心流行定理得到了计算Hopf分支方向和周期解稳定性的公式和判别方法.最后，通过数值模拟验证了理论的科学性.

前面的论证对进一步研究做好了准备工作，还有许多未开发的理论需要进一步探索.影响消费者购买量的还有居民的消费水平、物价.消费者的购买水平是有限的，所以购买量不可能随着广告量无限制的增涨，可以修改购物水平函数的线性分式函数，从而建立新的更准确的描述广告量-购物水平之间关系的函数.本文的研究结果可作为数理经济学和商业管理的定性分析的工具，为以后的研究做好铺垫.

[1] 王树禾. 微分方程与混沌[M]. 合肥: 中国科学技术大学出版社, 1999. 312-324.

[2] 张锡藩, 陈 侠, 陈筠青. 物价的微分方程模型的定性研究[J]. 沈阳航空工业学院学报, 2004, 21(1): 83-86.

[3] ZHAI Y H, BAI H Y, XIONG Y,etal. Hopf bifurcation analysis for the modified rayleigh price model with time delay [J]. Abstract and Applid Analysis, 2013, 2013(3): 432-445.

[4] 张锦炎, 冯贝叶. 常微分方程几何理论与分支问题[M]. 第二次修订版.北京: 北京大学出版社, 2000.

[5] 张锦炎. 失稳与分支(二维)[J].北京大学学报:自然科学版,1981(6)：40-42.

[6] 徐 鉴. 时滞系统动力学近期研究进展与展望[J]. 力学进展, 2006, 36(1): 17-30.

[7] HASSARD B D, KAZARINOFF N D, WAN Y H. Theory and applications of Hopf bifurcation [M]. Cambridge: Cambridge University Press, 1981.

[8] WEI J J, RUAN S G. Stability and bifurcation in a neural network model with two delays [J]. Physica D Nonlinear Phenomena, 1999, 130(3-4): 255-272.

Study on Hopf bifurcation and stability for advertising-shopping level model with delay

WANG Xiao-hong1, ZHAI Yan-hui1, GUO Wei2

(1. School of Science, Tianjin Polytechnic University, Tianjin 300387, China; 2. School of Biological Engineering, Tianjin University of Science & Technology, Tianjin 300457, China)

The model of Hopf bifurcation of advertising-shopping and stability with time delay was studied. By applying of the theory of hopf bifurcation and functional differential equation method, this paper discussed the linear stability of the model and the local Hopf bifurcation. The time delay was considered as a bifurcation parameter. By using the normal form theory and center manifold methods, the calculation formula was obtained for determining direction of Hopf bifurcations and bifurcating periodic solution stability. The numerical simulation showed the effectiveness of the conclusion.

advertising-shopping level model; time delay; Hopf bifurcation; stability

2016-03-19.

王晓红(1990-)，女，硕士，研究方向：微分方程动力系统.

O193

A

1672-0946(2017)01-0102-05