用于变压器负载能力评估的改进热电类比模型*

唐文虎 钱瞳 黄晶晶 陆国俊 王勇 栾乐

(1．华南理工大学 电力学院， 广东 广州 510640； 2．广州供电局有限公司， 广东 广州 510620)

在当前智能电网的背景下，运行调度部门对变电设备(变压器、断路器、隔离开关等)的动态增容有了进一步的需求.其中，变压器负载能力是制约电网变电容量限额的主要因素[1].当变电站出现“N-1”事故时，如果变压器有较高的负载能力，不仅可以使变压器在一定过载范围内安全稳定地运行，还可以给调度留出时间裕度[2].变压器绕组的热点温度是限制其负载能力的主要决定因素，它与负载电流、负载损耗和杂散损耗等有关[3].热点温度超过该处绝缘水平所能允许的长期平均温度时会破坏绝缘或导致寿命损失.因此，变压器负载能力研究的实质是分析变压器在热点温度不超过温度限值且不影响正常使用寿命的情况下所能承载的最大负荷及可持续时间的问题.

为了计算变压器的热点温度或顶层油温，国内外学者主要在3个方面进行研究.①数值仿真计算.有限元法与有限差分法的应用与发展使得在变压器温度计算领域已经能够利用这些方法较为精确地计算变压器各部件局部发热点的位置与温度，这对于变压器厂商合理设计与保护变压器而言是十分有效的[4].但此方法计算量大，求解的边界条件不容易确定，参数条件的微小改变都可能使计算结果产生大的变化；且对变压器负载能力有计算需求的电网运行部门难以获得变压器的具体参数，故该方法的通用性有限.②变压器负载导则温升计算.IEEE导则的温升指数模型[5]在电网运行部门中广泛使用，该模型被描述为指数模型，温升用差分方程表示，计算简便、通用性高.然而，一些研究学者也指出导则方法的缺点：过于依赖变压器试验报告的数据、不能反映环境温度的动态变化[6].③热电类比模型.其通过将热参数与电参数进行对应，参照电路模型构建变压器热传导的热路模型，成功地计算了变压器内部关键位置的温度值，并具备一定的准确性[7- 9].尽管Susa等[10- 11]已经考虑了变压器油黏度对油非线性热阻的影响,但是需要测量很多其他的变压器结构参数，而这些参数往往不易测量，从而限制了该模型在实际中的使用.Tang等[12- 13]提出了一种由油箱、绕组、铁芯和绝缘油4个部分组成的热电类比模型，并用两套热参数来反映变压器在冷却器开和关这两种冷却状态下的热传递过程，计算准确性高，但该模型对环境温度的变化缺乏响应能力.

由于热电类比模型能够与现行的变压器运行监测数据(顶层油温、绕组温度等)相关联，简便实用且物理意义清晰，因此文中从一种计算准确性效果较高的变压器简化热电类比模型出发，基于传热学原理和热电类比方法，用集中参数组成的热路模型反映变压器内部的传热过程.由于变压器温升相对于环境温度有着明显的滞后，不能直接响应环境温度的动态变化，所以考虑将油温升节点的温升值替换成实际温度值，并且把环境温度视为热路中的一个理想的“温度源”.取样测量变压器油的粘度，绘制油黏度随温度变化的曲线.引入油黏度重新定义非线性热导，考虑油黏度对变压器内部散热性能的影响.文中首次将改进的热电类比模型应用于变压器的负载能力评估，并研究影响变压器负载能力的因素及对应的关系，为油浸式电力变压器动态增容提供参考.

1 电力变压器热电类比模型

Tang等[12- 13]提出了一种油浸式变压器的5节点等效热路模型，并考虑到在线监测油温数据的限制，将其简化成了3节点的等效热路模型，如图1所示.铁芯、绕组和部分绝缘油的热容组成了“集总热容”C1，分散的铜耗PCu、铁耗PFe、杂散损耗Pad用整体的热源Pall来表示.温升节点θ1表示变压器油相对环境温度的平均温升，θ2和θ3分别表示顶层油温升和底层油温升.C2和C3分别表示顶层油温升节点和底层油温升节点对环境温度的集总热容.G1、G2和G3表示相关联温升节点之间的等效热导，如G2表示θ2和θ3之间的等效热导.

变压器的非线性热导与变压器的很多物理参数有关，如实际几何尺寸、热特征参数等[14- 16].因此，选择一个能反映其非线性本质的表达式至关重要.根据相关研究经验[12]，它们被指数形式的公式描述如下：

G=aΔθb

(1)

其中，G是热导矩阵中的一个元素，Δθ表示研究部件两端的温差，a和b是需要优化的参数.

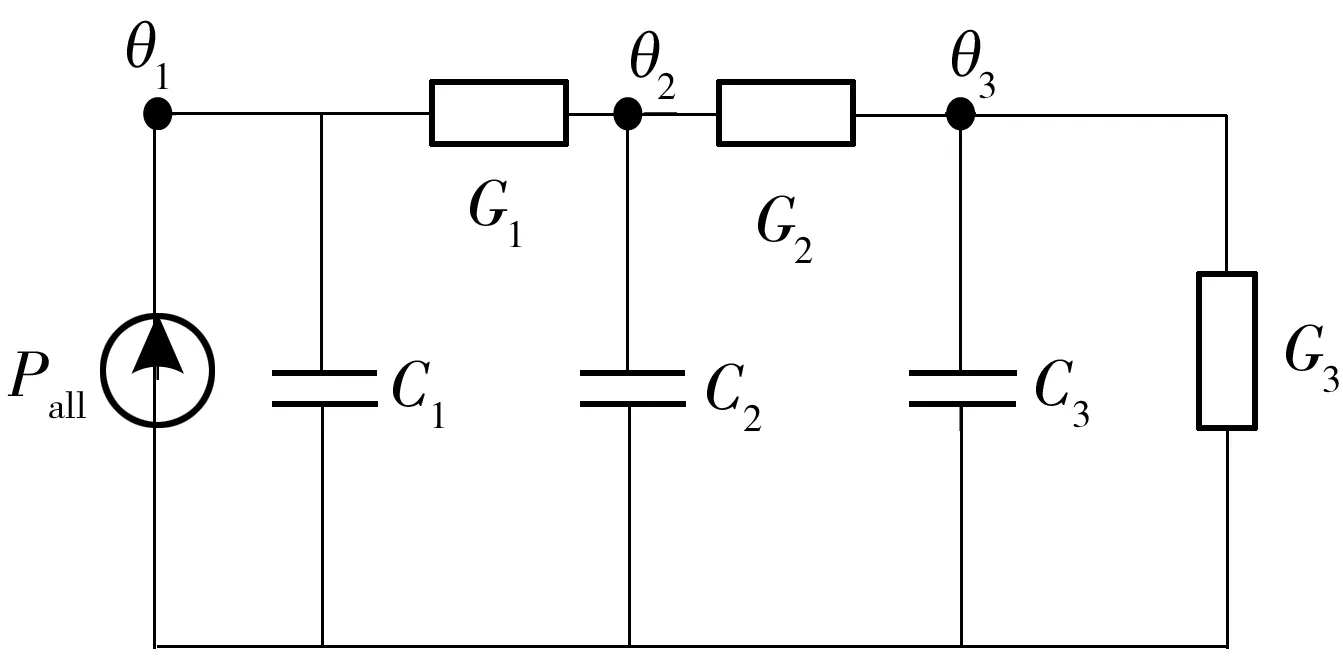
图1 简化的等效热路模型Fig.1 Simplified equivalent heat circuit of thermal model

2 改进的热电类比模型

2.1 温升节点的修正

在Tang等[12- 13]简化的热电类比模型中，环境温度变化并没有被直接考虑，而是通过各部件温升在一定时间范围内的平均值来间接衡量.节点θ1是变压器油的平均温升，难以体现变压器内部热传导的动态过程.

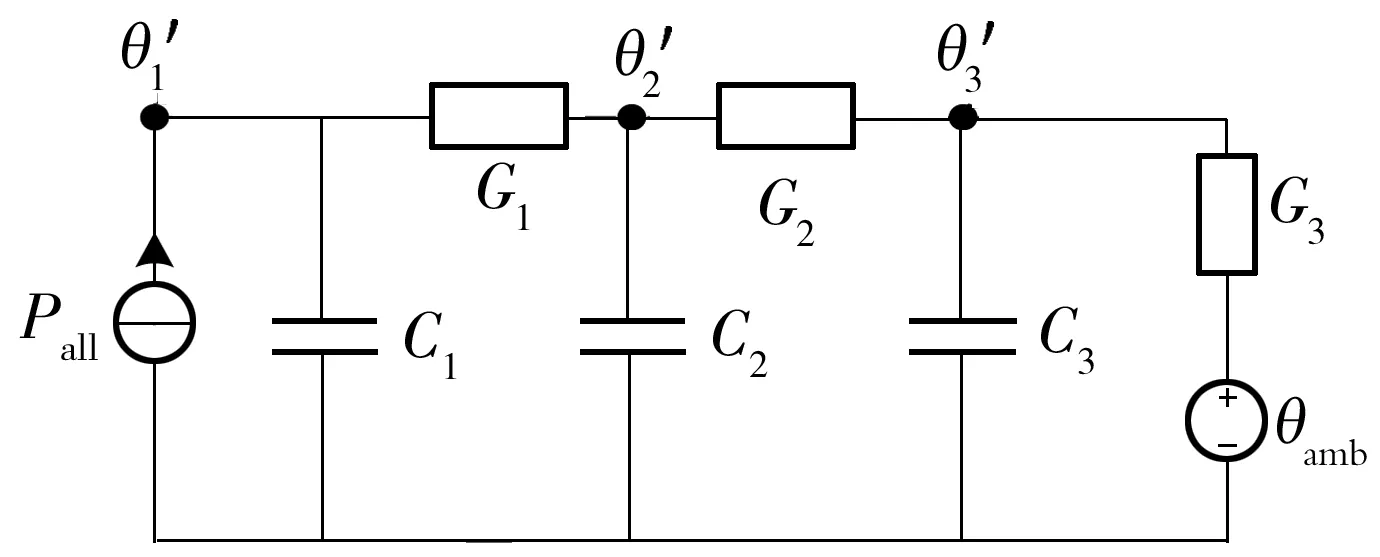
图2 改进后的等效热路模型Fig.2 Improved equivalent heat circuit of thermal model

2.2 非线性热导的修正

根据热传递理论，变压器热电类比模型中的非线性热阻定义如下[17- 18]：

(2)

式中：h是热传递系数；A是接触面积；Δθoil是油温差；q是相应的损耗.

由传热学方程可得：

(3)

其中：L是特征尺寸(长度、宽度或者直径)；k是油的导热系数；g是重力加速度；ρoil是油的密度；β是膨胀系数；coil是油的比热容；μ是油黏度；C和n是经验常数，取决于油循环是层流还是湍流.

变压器油的密度、比热容等热特征参数值随着温度的变化而改变，其中，油黏度值的变化最为显著，而其他热特征参数变化很小[16].因此，除了油黏度外，其他的参数可视为常量.这样，传热系数h可写为

(4)

其中，Q为常数，表示为

(5)

这样，变压器油的非线性热导可以写为

(6)

参考式(2)，变压器油的非线性热导可以修改为

(7)

其中，a表示QA的值，b表示n值.油黏度μ取研究部分两端平均油温下的油黏度值.对于与热导G1和G2相关的油黏度μ1和μ2，有如下表示：

(8)

因此，对于图2的改进热模型，热导矩阵表示为

(9)

其中aj、bj(j=1，2，3)是与热导Gj有关的常数，需要通过优化来确定.

2.3 模型的参数优化

为了得到模型的热特征参数(aj、bj、Cj),通常需要通过一系列的试验分析.但是，对运行中的变压器做离线温升试验是不可行的.另外，如果变压器已经运行了若干年，绝缘性能和各类参数可能会发生变化，出厂温升试验报告的数据难以准确反映变压器的热过程.因此，为了不依赖于温升试验数据，考虑用遗传算法结合变压器的在线监测数据优化模型中的热特征参数.

2.3.1 遗传算法

遗传算法是一种基于自然选择机理的优化算法，通过控制3种遗传算子——选择、交叉、变异来产生下一代个体，有很好的全局搜索能力[9].

2.3.2 适应度函数

使用遗传算法搜索热模型的参数，需要定义合适的适应度函数，使其能够量化模型计算结果与在线监测数据的误差.对于文中改进的变压器热电类比模型，适应度函数f应包含3个子函数，分别用来计算热点温度误差fHST、顶层油温误差fTOT和底层油温误差fBOT，表示如下：

(11)

变压器热模型总的适应度函数定义为

(12)

式中，w1、w2和w3分别为各个子适应度值占总适应度值的权重，根据实际的关切程度，这里分别取为1/2、1/3、1/6.

2.4 案例分析

为了验证改进模型的准确性，文中选取了一台ONAN(油浸自冷)/OFAF(强迫油循环风冷)冷却方式的电力变压器，铭牌信息如表1所示.从该变压器中抽取油样，测量不同油温下的油黏度值，如表2所示.据此拟合出的油黏度随油温变化的曲线如图3所示.

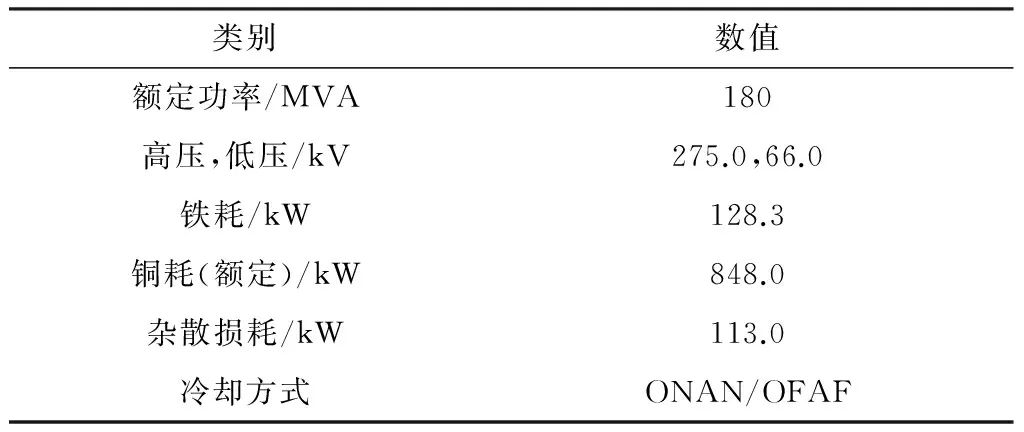
表1 所研究的变压器的铭牌信息Table 1 Nameplate of the studied power transformer

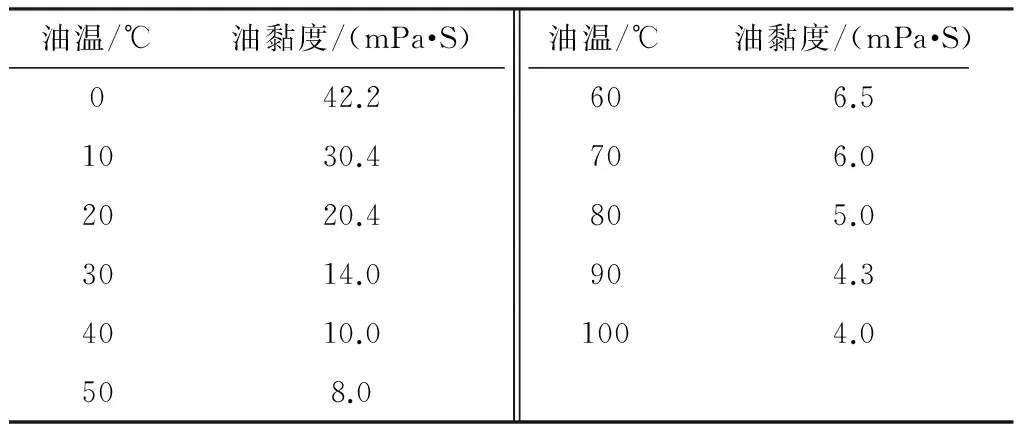
表2 不同油温下的油黏度值1)Table 2 Oil viscosity values of different oil temperature

1)表格中的每个油黏度均为4次取样得到的平均值.

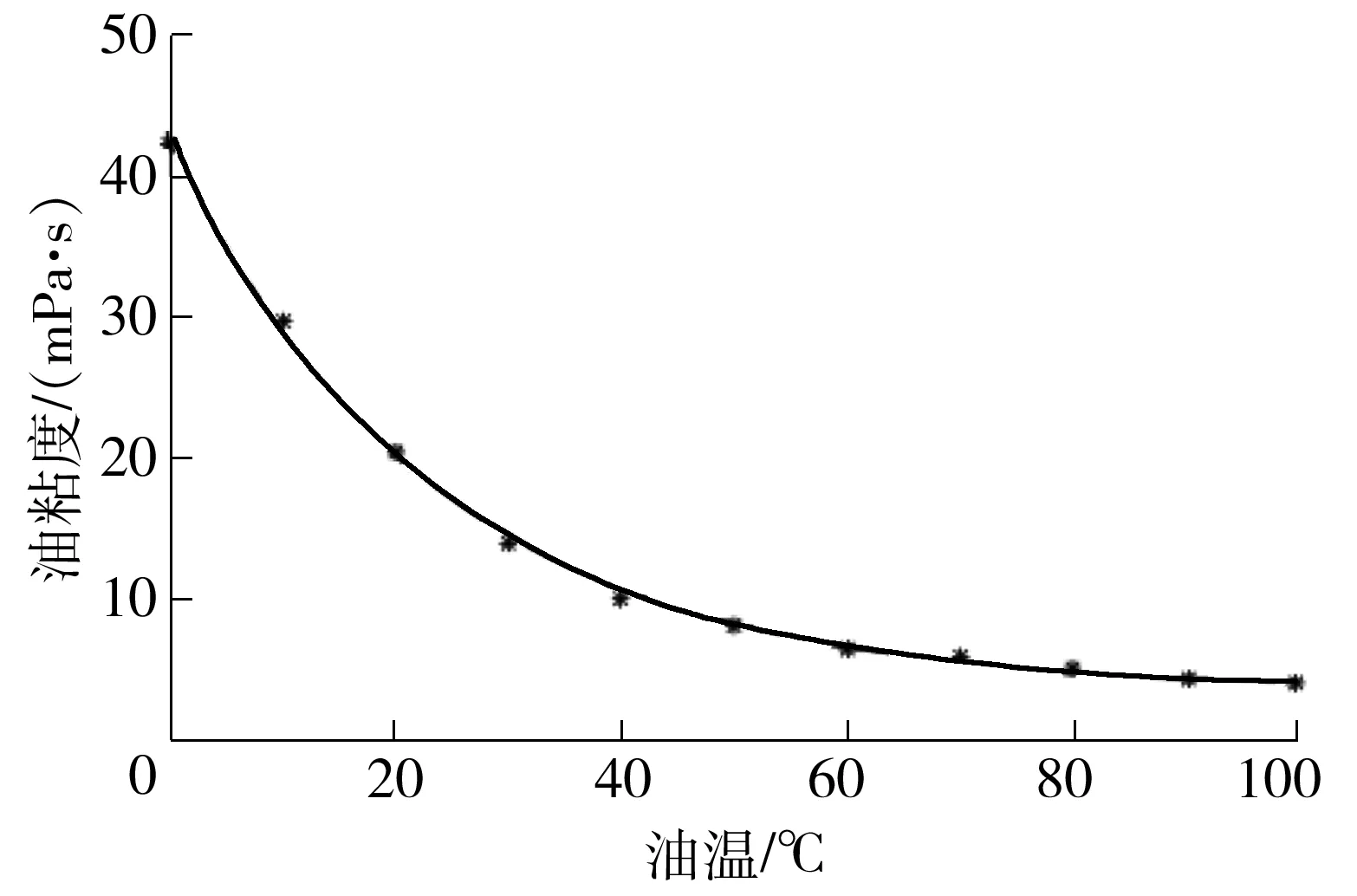
图3 油黏度拟合曲线Fig.3 Fitting curve of the oil viscosity

图3所示的拟合得到的油黏度曲线的表达式为

μ=3.43+39.31e-0.04θ

(13)

其中，θ表示变压器油温.

提取该变压器的4 364组在线监测数据作为样本集，样本之间的时间间隔为1 min，每个样本数据包括负载率、环境温度、底层油温、顶层油温、热点温度，其中前3 121组为冷却器开时的样本，其余1 243组为冷却器关时的样本.监测的环境温度和负载率变化情况如图4所示.

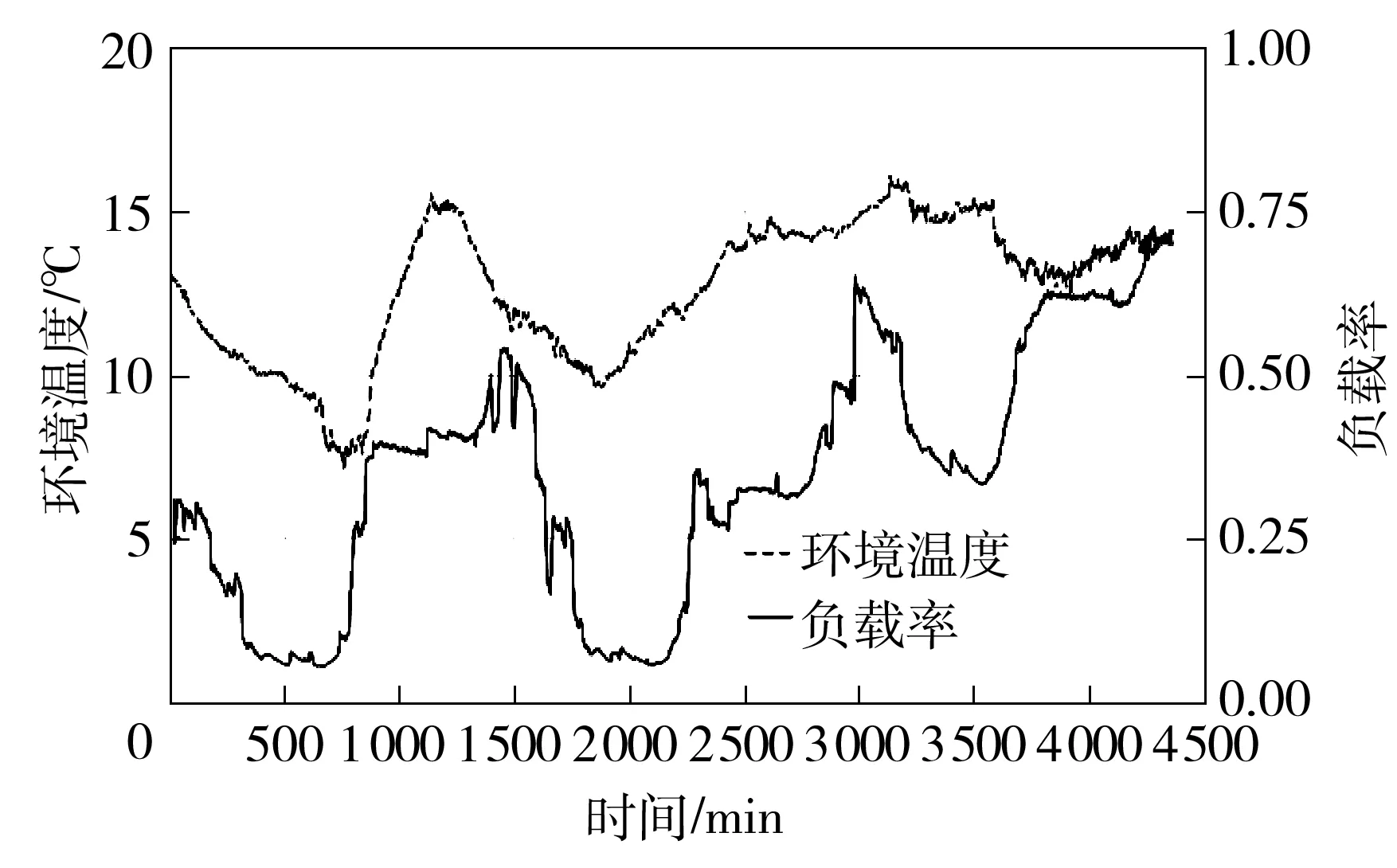
图4 实时环境温度和负载率Fig.4 Real-time ambient temperature and load ratios

从样本集中取约30%(第2 201 min到3 500 min，共计1 300个样本)的数据用于构建、优化改进前和改进后模型的参数.将其中的环境温度、负载率、冷却器的开关状态作为模型输入量，底层油温、顶层油温、热点温度作为模型的输出量，借助遗传算法优化模型参数.设置遗传算法的交叉概率为0.95，变异概率为0.08，种群数量为100，最大进化代数为200.改进后模型的热参数经优化后如表3所示，改进前模型的热参数类似文献[10].

表3 改进后模型参数Table 3 Parameters of the improved model

导则推荐计算热点温度θh的公式如下[5]：

(14)

其中，ΔθT,R是额定负载下的顶层油温，K是负载率，R是损耗比(额定负载损耗与空载损耗的比值)，x是与冷却有关的指数(ONAN时为0.8，OFAF时为0.9)，y是总损耗对顶层油温升的指数(常数1.6)，Hgr是热点温度与顶层油温之差(ONAN时为26 ℃，OFAF时为22 ℃).改进前模型未直接计算热点温度，而是在计算的顶层油温基础上参考导则公式加HgrKy得到的.

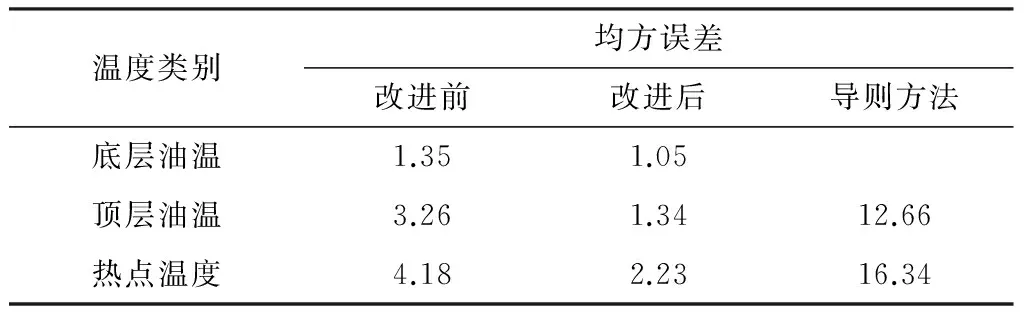
基于完整的样本集(4 364组)，利用表3所示参数构建的改进后模型以及文中重新构建的改进前模型的结果，与通过变压器导则方法得到的计算值(导则未考虑底层油温计算)以及实际监测值的比较如图5所示.不同方法计算值相对于监测值的均方误差见表4.

由图4和图5可知，负载率的增大会导致底层油温和顶层油温上升.底层油温受负载率和环境温度变化的影响相对较小，受冷却器开、关的影响较大.从图5和表4中可以看出，改进前模型对变化平缓的底层油温计算精度良好，而对于波动较大的顶层油温、热点温度则计算精度较差.相比较于改进前的变压器热电类比模型，改进后的模型计算得出的底层油温、顶层油温和热点温度都更加贴近实际的监测值，说明改进后的模型在环境温度变化、负载波动、冷却器状态切换的实际运行工况下，较原有模型能更灵敏、更准确地反映变压器内部的热传递过程.从图5的变压器负载导则的顶层油温和热点温度计算结果来看，其误差明显大于文中讨论的热电类比模型，且在冷却器切换时动态响应严重不足(如图5显示，通过导则计算的顶层油温和热点温度在冷却器切换时出现异常尖峰).另外，注意到通过导则计算得到的热点温度大部分时间明显高于改进后模型和实际监测的结果，因为导则模型未考虑油黏度随油温的升高而减小(如表2所示，变压器油在80 ℃时的油黏度值只有10 ℃时的1/6左右)对变压器内部换热的影响，弱化了变压器油的实际热传导能力，使得热点温度计算值偏高.鉴于改进后热电类比模型的优越表现，以及变压器负载导则计算方法的不足，考虑用改进热电类比模型进行负载能力评估研究.

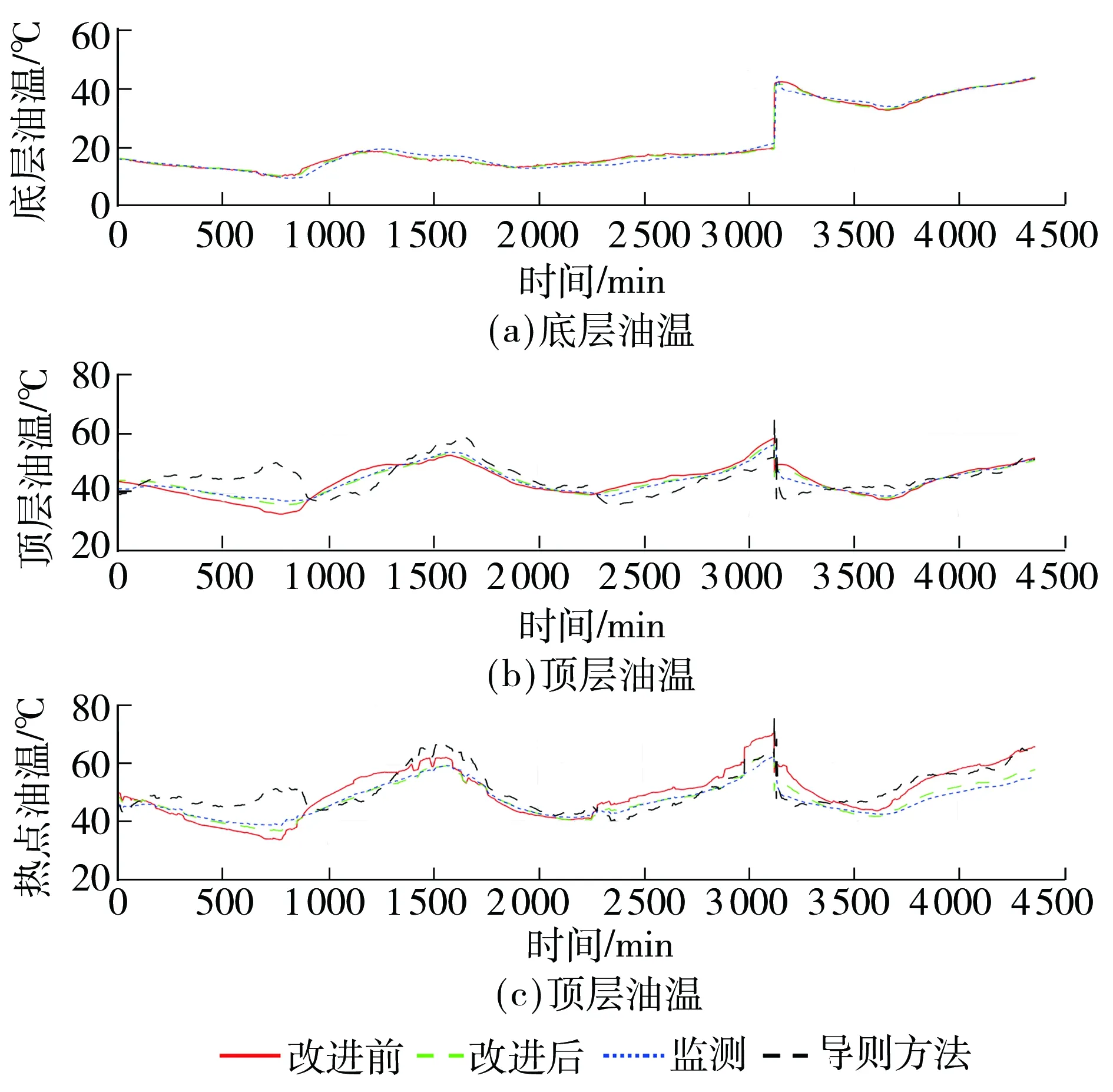
图5 改进前、后模型以及变压器导则计算的底层油温、顶层油温、热点温度与在线监测值的对比

Fig.5 Comparison of top-oil temperature,bottom-oil temperature and hot-spot temperature of the improved thermal-electrical model,the original model,the transformer loading guide and the onsite measurements

表4 不同方法计算值相对于监测值的均方误差

Table 4 Mean square errors between the monitored temperature and the calculated values obtained through different methods

温度类别均方误差改进前改进后导则方法底层油温1.351.05顶层油温3.261.3412.66热点温度4.182.2316.34

3 负载能力评估

变压器的负载能力是指其能够维持本身正常寿命而在某一段时间内所允许承担的最大负载.为保证变压器正常的使用年限，该负载值通常是根据等值热老化原理来确定，即变压器在过载时间内所缩短的寿命等于或者小于其在欠载时间内所延长的寿命.另外，变压器过载运行时内部的温度不应超过其允许的绝缘耐受限制[5,19].

变压器相对老化率公式为

V=2(θHST-98)/6

(15)

式中，θHST为变压器热点温度.

相对寿命损失：

(16)

式中,t1、t2为相对老化率作用时间范围.

IEC推荐的等效二级矩形负荷分布如图6所示.在文中使用的日负荷等效分布中，将图6的负载率K1和K3都设置为0.5，t1为12 h，t2为14 h，也即模拟了一个日负荷分布场景：变压器半负载运行12 h，然后过载运行2 h，最后再半负载运行10 h.通过3类限制(①顶层油温不超过115 ℃；②热点温度不超过140 ℃；③日相对寿命损失不超过1)来计算环境温度分别恒定在0、20、40 ℃时，该变压器所能承载的最大负荷率K2.基于表2中参数构建的热电类比热模型以及式(14)、(15)，计算流程如图7所示，其中m为样本序数，1 min 1个样本，24 h共1 440个样本.图8所示是环境温度为0 ℃时，随着负载率K2的增大，相应的等效日负荷分布下的最大顶层油温、最大热点温度以及日相对寿命损失的变化情况.环境温度恒定在0、20、40 ℃时,分别计算得出的最大可允许的负载率K2及其在该负载率下的最大顶层油温、最大热点温度和日相对寿命损失如表5所示.

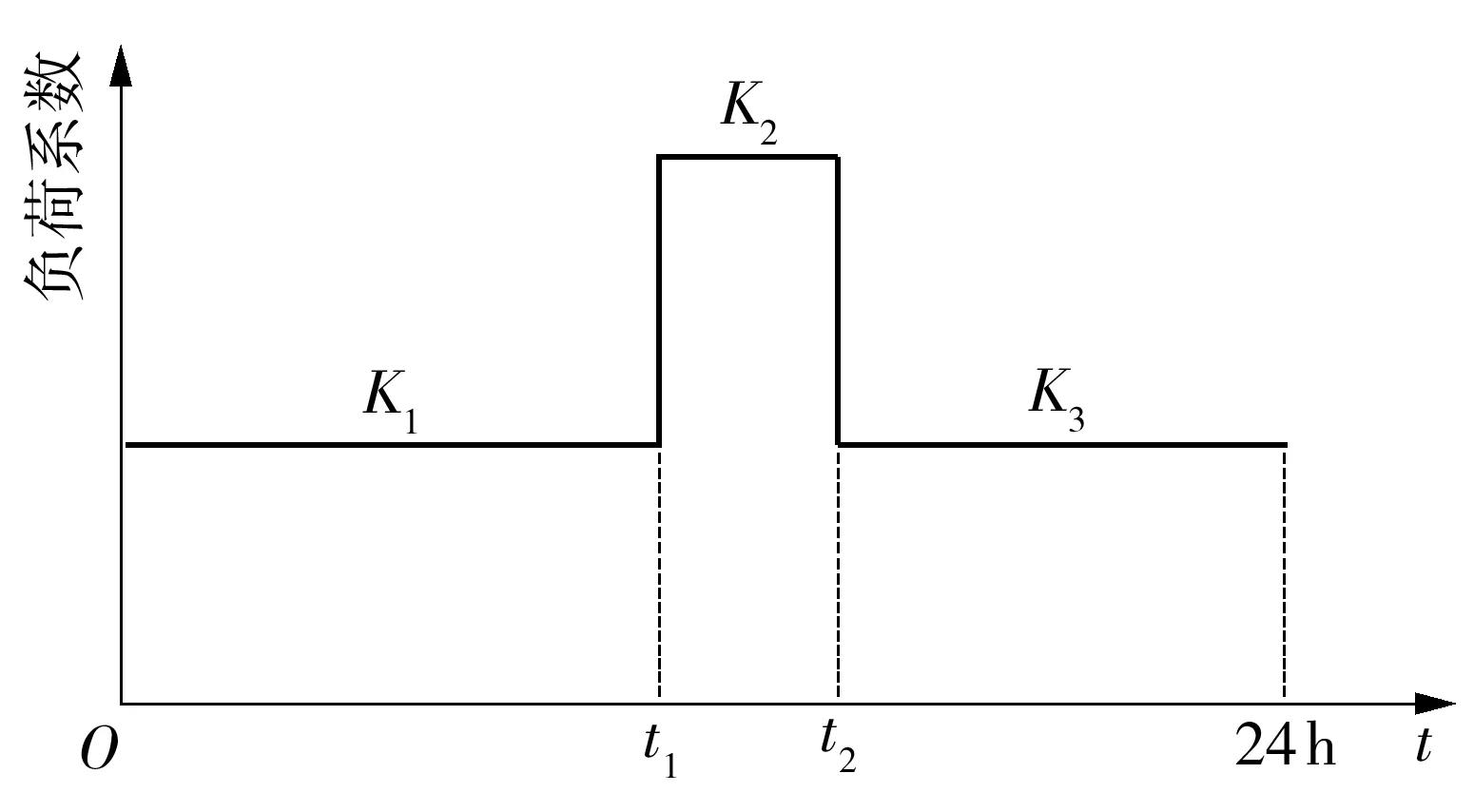
图6 日负荷等效分布Fig.6 Equivalent distribution of daily load

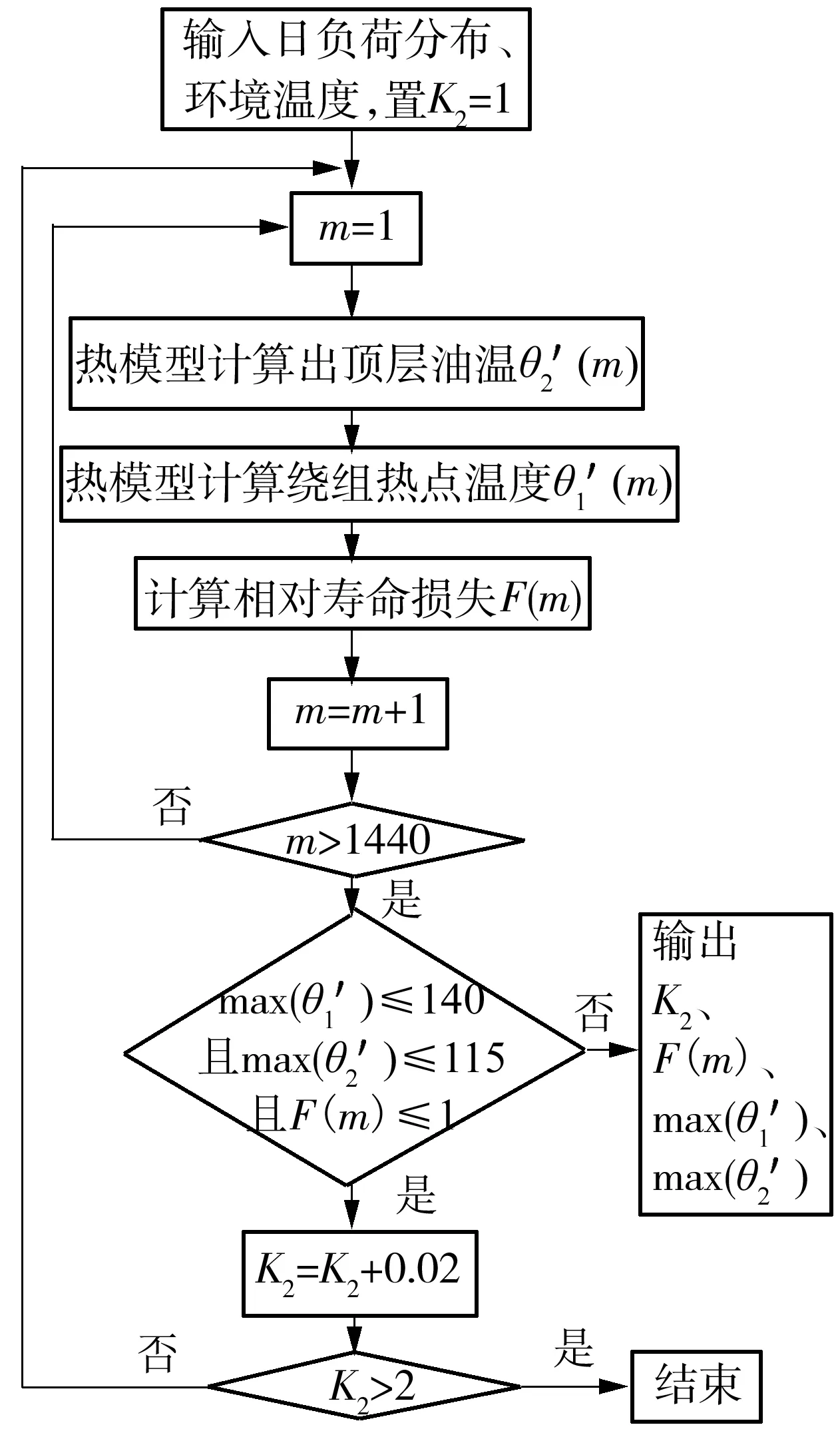
图7 变压器负载能力计算流程Fig.7 Calculation process of transformer load capacity

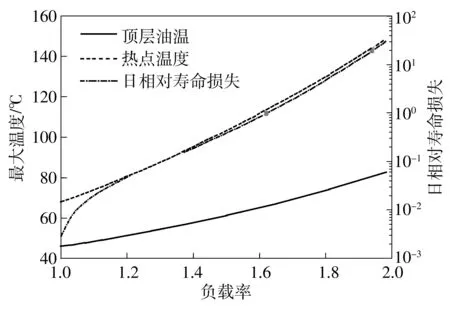
图8 最大顶层油温、最大热点温度、日相对寿命损失随负载率的变化情况

Fig.8 Maximum top-oil temperature,maximum hot-spot temperature and relative daily loss of life versus with load changes

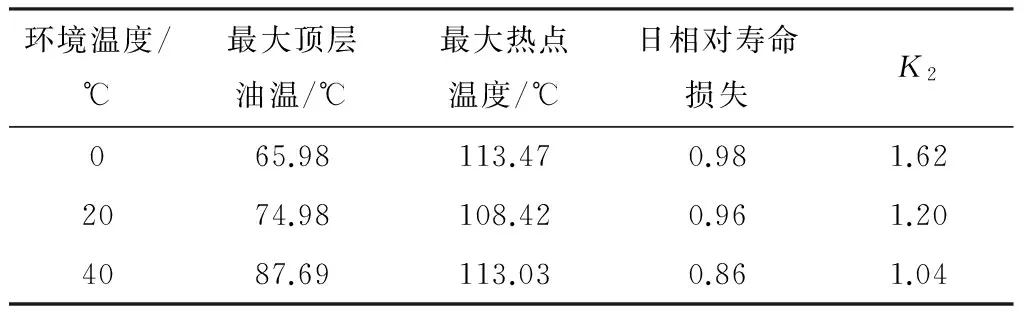
表5 不同环境温度下允许最大过载倍数及具体的限值

Table 5 Maximum allowable overload and its specific limits under different environment temperatures

环境温度/℃最大顶层油温/℃最大热点温度/℃日相对寿命损失K2065.98113.470.981.622074.98108.420.961.204087.69113.030.861.04

由图8可见，负载率K2从额定负载增大到两倍额定负载的过程中，顶层油温没有超过限制.热点温度和日相对寿命损失都超过了限制，后者最先达到限值.其中，不超过热点温度限制的最大K2是1.90，不超过日相对寿命损失限制的最大K2是1.62.因此，当环境温度恒定在0 ℃时，利用改进的热电类比模型，基于设定的日负荷等效分布，最大可允许1.62倍过负载运行.同时注意到，当一天的环境温度恒定时，负载率K2每增加0.02，热点温度大约增加1.7 ℃.从表5的结果可以看出，环境温度的改变直接影响着变压器的过载能力，环境温度高时，变压器周期性过负载能力比环境温度低时要低.而且可以发现，环境温度越高，变压器的日相对寿命损失随负载率K2增大而增加得越明显.例如，环境温度为40 ℃时，最大可允许的负载率K2为1.04，此时日相对寿命损失为0.86，而K2为1.06时的日相对寿命损失已经增加到超过1(由图7的计算流程仿真计算得到)，相比较0 ℃和20 ℃，增加更为迅速.

4 结语

文中采用改进后模型计算得出的热点温度、顶层油温和底层油温相比较改进前模型误差更小，尤其是对波动较大的顶层油温和热点温度的计算准确度提升更明显.这些结果反映了改进后的模型与变压器实际的内部发热过程更加吻合，也验证了文中引入环境温度对变压器散热影响以及构建的非线性热导的合理性.在利用改进后模型进行负载能力研究时，发现随着负载率的增加，日相对寿命损失限制是最先达到的，应该对变压器的寿命作进一步研究.文章的不足之处在于确定最大负载率时尚未考虑变压器的故障率、经济损益等限制条件，且所研究的日负荷只是一个典型的等效日负荷.但文中研究的热模型不局限于所研究的变压器，其他类型的变压器也可根据此思路来建立热电类比模型并进行负载能力研究.

[1] 凌平，黄华．变电设备动态增容方案设计研究 [J]．华东电力，2011，39(11)：1799- 1802．

LING Ping,HUANG Hua.Research on variable dynamic capacity plan design of electric equipment [J].East China Electric Power,2011,39(11):1799- 1802.

[2] 油浸式变压器(电抗器)状态评价导则：Q/GDW- 11- 106—2007 [S].

[3] 范闻博，韩筛根．有载调容变压器安全经济运行控制策略 [J]．电力系统自动化，2011，35(18)：98- 107．

FAN Wen-bo,HAN Shai-gen.A control strategy for secure and economic operation of on-load capacity regulating transformer [J].Automation of Electric Power System,2011,35(18):98- 107.

[4] 苏小平，陈伟根，胡启元，等.基于解析-数值技术的变压器绕组温度分布计算 [J].高电压技术，2014，40(10)：3164- 3170.

SU Xiao-ping,CHEN Wei-gen,HU Qi-yuan,et al.Calculation for transformer winding temperature distribution by numerical analytical technology [J].High Voltage Engineering,2014,40(10):3164- 3170.

[5] IEEE Guide for determination of maximum winding temperature rise in liquid-filled transformers：IEEE Standard 1538—2000 [S].

[6] TYLAVSKY D J,HE Q,MCCULLA G A.Sources of error in substation distribution transformer thermal modeling [J].IEEE Transactions on Power Delivery,2000,15(1):178- 185.

[7] RADAKOVIC Z,CARDILLO Z,SCHAEFER M.Design of the winding-bushing interconnections in large power transformers [J].Electrical Engineering,2006,88(3):183- 190.

[8] SWIFT G,MOLINSKI T,LEHN W.A fundamental approach to transformer thermal modeling(I)：theory and equivalent circuit [J].IEEE Transactions on Power Delivery,2001,16(2):171- 175.

[9] SWIFT G,MOLINSKI T,BARY R，et al.A fundamental approach to transformer thermal modeling(II):field verification [J].IEEE Transactions on Power Delivery,2001,16(2):176- 180.

[10] SUSA D,NORDMAN H.A simple model for calculating transformer hot-spot temperature [J].IEEE Transactions on Power Delivery,2009,24(3):1257- 1265.

[11] SUSA D,LEHTONEN M,NORDMAN H.Dynamic thermal modelling of power transformers [J].IEEE Transac-tions on Power Delivery,2005,20(1):197- 204.

[12] TANG W H,WU Q H,RICHARDSON Z J.A simplified transformer thermal model based on thermal-electric analogy [J].IEEE Transactions on Power Delivery,2004,19(3):1112- 1119.

[13] TANG W H,WU Q H,RICHARDSON R.Equivalent heat circuit based power transformer thermal model [J].Electric Power Applications Iee Proceeding,2002,149(2)：87- 92．

[14] 江淘莎，李剑，陈伟根，等．油浸式变压器绕组热点温度计算的热路模型 [J]．高电压技术，2009，35(7)：1635- 1640．

JIANG Tao-sha,LI Jian,CHEN Wei-gen,et al.Thermal model for hot spot temperature calculation in oil-immersed transformers [J].High Voltage Engineering,2009,35(7):1635- 1640.

[15] 滕黎，陈伟根，孙才新．油浸式电力变压器动态热路改进模型 [J]．电网技术，2012，36(4):236- 241．

TENG Li,CHEN Wei-gen,SUN Cai-xin.An improved dynamic thermal circuit model of oil-immersed power transformer [J].Power System Technology,2012,36(4):236- 241.

[16] LEISURE B,HAGMAN W,KIRTLEY J.An improved transformer top oil temperature model for use in an on-line monitoring and diagnostic system [J].IEEE Tran-sactions on Power Delivery,1997,12(1):249- 256.

[17] 王秀春，刘伟军，朱恒宣，等．油浸式变压器层式绕组温度场研究 [J]．变压器，2010，47(10)：44- 48．

WANG Xiu-chun,LIU Wei-jun,ZHU Heng-xuan,et al.Research on temperature field of layer-type winding in oil-immersed transformer [J].Transformer,2010,47(10):44- 48.

[18] 苏小平．油浸式变压器绕组热点温度计算模型及预测方法研究 [D]．重庆：重庆大学，2012.

[19] 电力变压器第7部分：油浸式电力变压器负载导则:GB/T1094.7—2008 [S]．