考虑变粘性系数的MHD驻点流解析解

李明军, 李胜男, 李桂波

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

计算数学

考虑变粘性系数的MHD驻点流解析解

李明军, 李胜男, 李桂波

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

研究变粘性系数的2维MHD驻点流问题。平板被放置在大小为H0的磁场中,对Navier-Stokes方程组进行计算,其中粘性系数是温度的函数。通过物理分析得到变粘性系数的MHD驻点流动的Navier-Stokes控制方程组。通过相似变换,将控制方程组转化为常微分方程组。数值分析了磁场效应和温度变化对壁面摩擦系数、壁面传热及流场特征等的影响,并得到了速度、磁场及温度随各参数的变化趋势。

驻点流;MHD流; 变粘性系数; 相似解; 打靶法

0 引 言

2维驻点流问题是流体力学中的一个经典问题,并且有广泛的应用领域。例如,均匀磁场下导电流体的驻点流问题在现代冶金和金属加工过程中起着非常重要的作用,因为其最终产品的质量往往取决于金属冷却速率,而这个速率又与壁面边界层结构有关。

Hiemenz[1]最先研究了经典2维平板驻点流问题,并且得到了N-S控制方程的精确解。从此,许多研究者对这个问题进行了不同方面的研究,例如3维驻点流问题、非定常驻点流问题、斜驻点流问题及带有热边界层的驻点流问题。Mahapatra等[2]对平板2维定常不可压粘性导电流体的MHD边界层方程给出了精确的相似解,研究了常温表面上的流体温度分布情况。Grosan[3]研究了固定平板MHD斜入射驻点流问题。在他的研究中,考虑了大小为常数的横向磁场。Lok等[4]研究了拉伸/收缩平板上粘性导电流体的MHD斜入射驻点流问题,其中外加磁场是均匀的,方向平行于斜入射驻点流的分界流线。Mahapatra等[5]考虑了收缩平板上斜入射驻点流的传热和辐射问题,研究发现流体内某一点的温度随着有效普朗特数的增加而减小。Chiam[6]表示出了拉伸表面驻点流边界层传热问题的相似解,并讨论了其对流场的影响,其中热传导系数随着温度线性变化。Ali等[7]扩展了此问题,考虑了感应磁场对流场的影响,研究了正交于拉伸平板的粘性不可压驻点流问题和常热传导系数的传热问题。Singh等[8]研究了固定横向磁场下MHD斜入射驻点流问题。

本文研究变粘性系数2维粘性不可压驻点流问题,其中粘性系数是温度的函数,同时考虑感应磁场对整个流场的影响。

1 基本方程组

本文考虑的2维定常粘性不可压流体在正交于固定平板y=0平面上流动,如图1所示。导电流体放置在外加磁场H中,同时考虑感应磁场的影响。根据文献[9],此问题的控制方程可以写为

(1)

(2)

(3)

(4)

图1 物理模型及坐标系Fig.1 Physical model and coordinate system

其中:x和y是沿平板表面及与其垂直平面建立的笛卡尔坐标;u和v是沿x和y轴的速度分量;H1和H2是沿x和y轴的磁场强度分量;ρ∞是流体密度;μ0是磁导率;σ是电导率;Cp是常压下的比热;ue(x)和He(x)是边界层边界的x轴方向速度分量和磁场强度分量;k∞是热传导系数。

本文中,粘性系数为T的函数,定义为

或

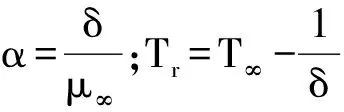
边界条件如下:

(5)

(6)

其中:a是大于零的常数;H0是外流场均匀磁场的大小。

引入下面的相似变换:

非线性偏微分方程组(1)～方程(4)可转化为如下常微分方程组:

(7)

(8)

边界条件(5)～条件(6)转化为

(9)

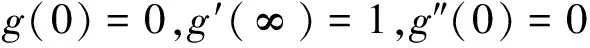
(10)

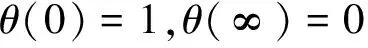
(11)

其中参数λ,Pr,β和θr分别表示磁普朗特数的倒数,普朗特数,磁参数和流体粘性参数。其定义为

当流体粘性系数为常数时,方程(7)退化为

该结果与Ali等[7]方程的结果一致。

本文关注的量为表面摩擦系数和努赛尔特数,分别定义为

2 结果与讨论

采用龙格-库塔方法和打靶法对方程(7)～方程(8)及其边界条件(9)～条件(11)进行数值求解。为了检验所使用数值求解方法的正确性和准确性,计算了粘性系数μ(T)取常数且不考虑磁场,即β=0时f″(0)的值。数值结果与Howarth[11]和Li等[12]的结果进行了对比,如表1所示。可以发现,计算结果与之前发表过的结果吻合良好,说明数值方法是准确的。

表1 f″(0)的数值(μ(T)为常数,β=0)

首先计算了表面摩擦系数f″(0)随磁系数β和流体粘性参数θr的变化。如图2所示,表面摩擦系数随着β的增加而减小,也随着-θr的增加而减小。图3给出了当地努赛尔特数-θ′(0)随Pr数变化情况,可以发现,-θ′(0)随Pr数的增加而增加。

图4～图6表示,当Pr=0.72,θr=-1时磁系数β对水平速度剖面f′(η)、感应磁场剖面g′(η)、温度剖面θ(η)的影响。可以看出,速度和感应磁场随着β的增加而减小,而温度随着β的增加而增加。

图7～图9表示,当Pr=0.72,β=0.1时粘性系数θr对水平速度剖面f′(η)、感应磁场剖面g′(η)和温度剖面θ(η)的影响。可以看出,速度和感应磁场随着-θr增加而减小,而温度随着-θr增加而增加。

图10～图12表示,当θr=-1,β=0.1时普朗特数Pr对水平速度剖面f′(η)、感应磁场剖面g′(η)和温度剖面θ(η)的影响,可以看出,速度、感应磁场和温度都随着Pr的增加而减小。

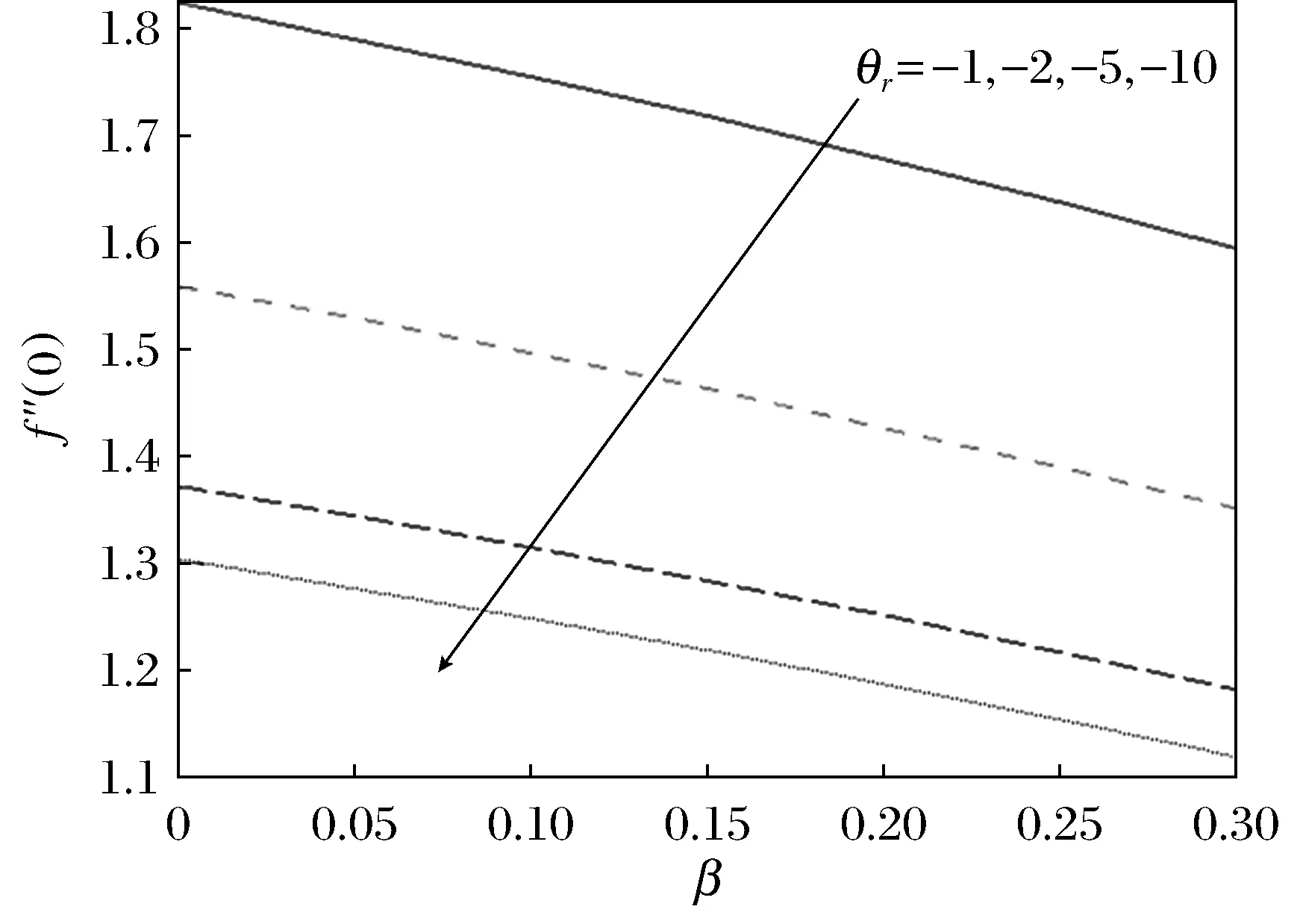
图2 Pr=0.72时,不同θr值对应的f″(0)随β的变化

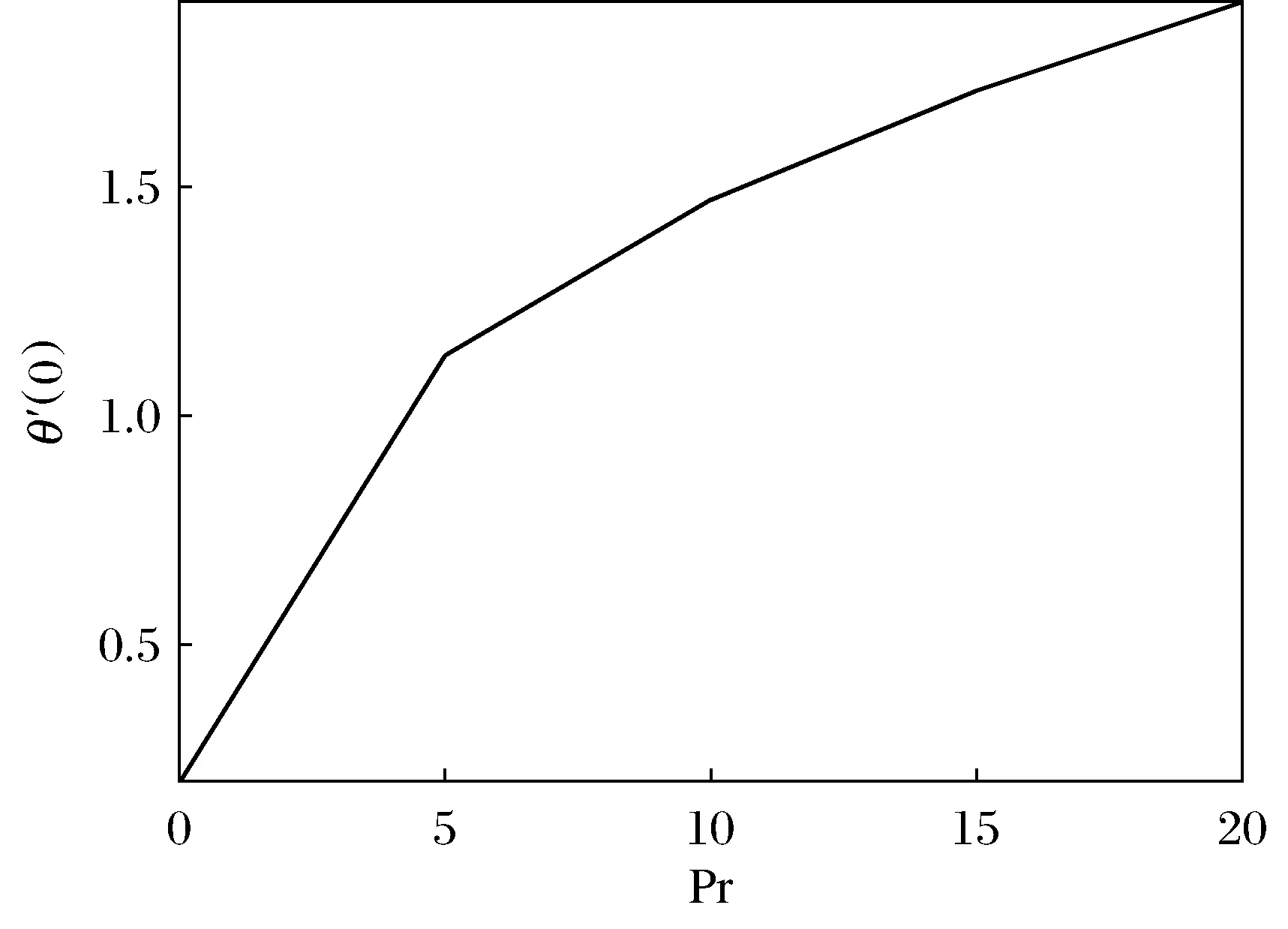
图3 -θ′(0)随Pr的变化

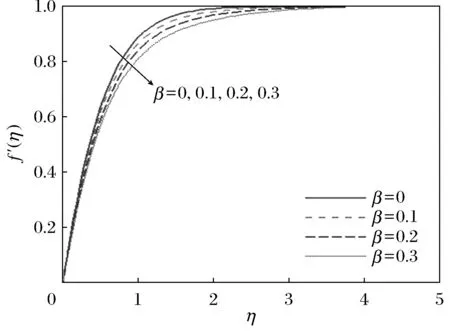
图4 Pr=0.72,θr=-1时,不同β值对应的f′(η)剖面

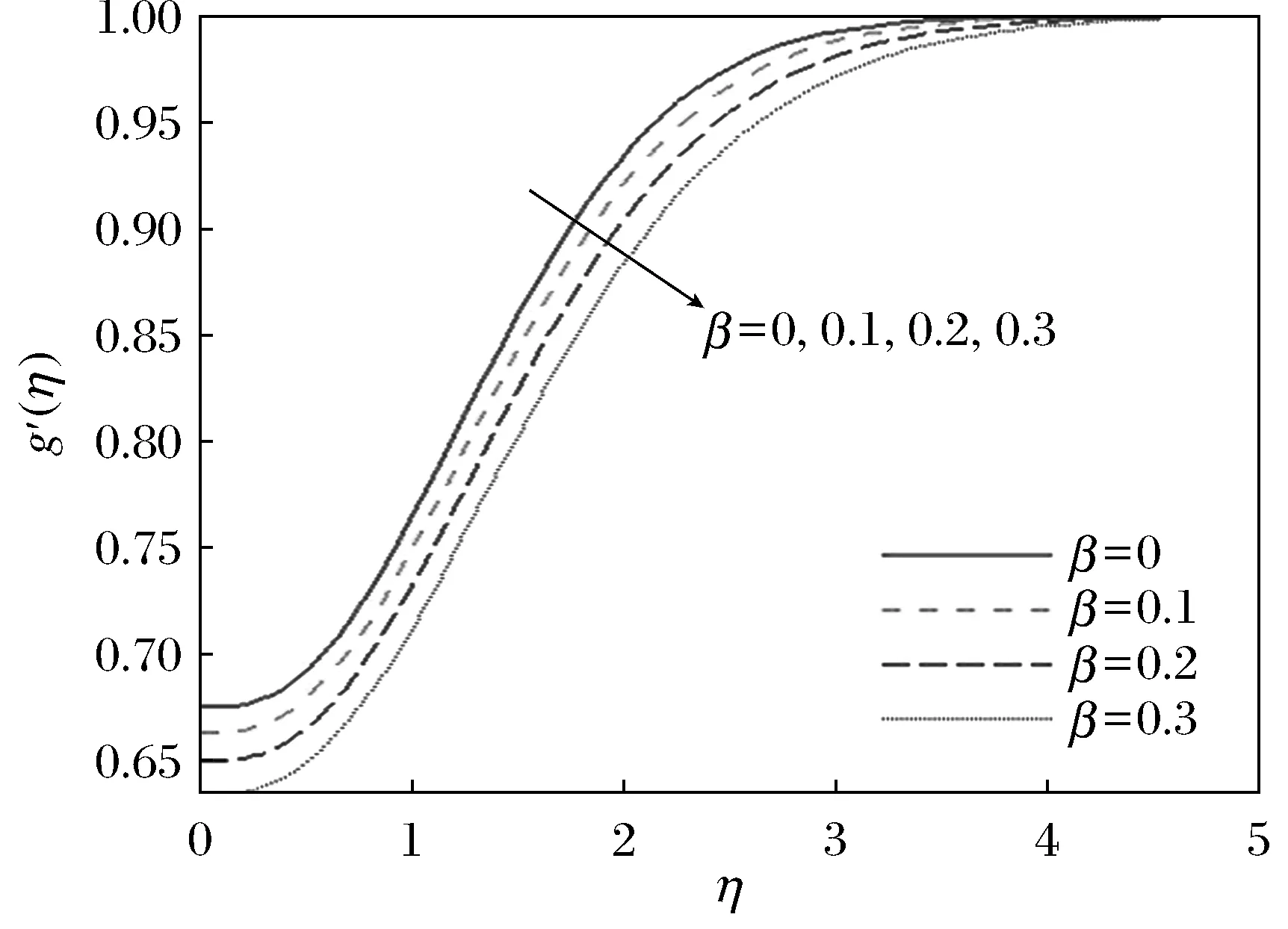
图5 Pr=0.72,θr=-1时,不同β值对应的g′(η)剖面

图6 Pr=0.72,θr=-1时,不同β值对应的θ(η)剖面

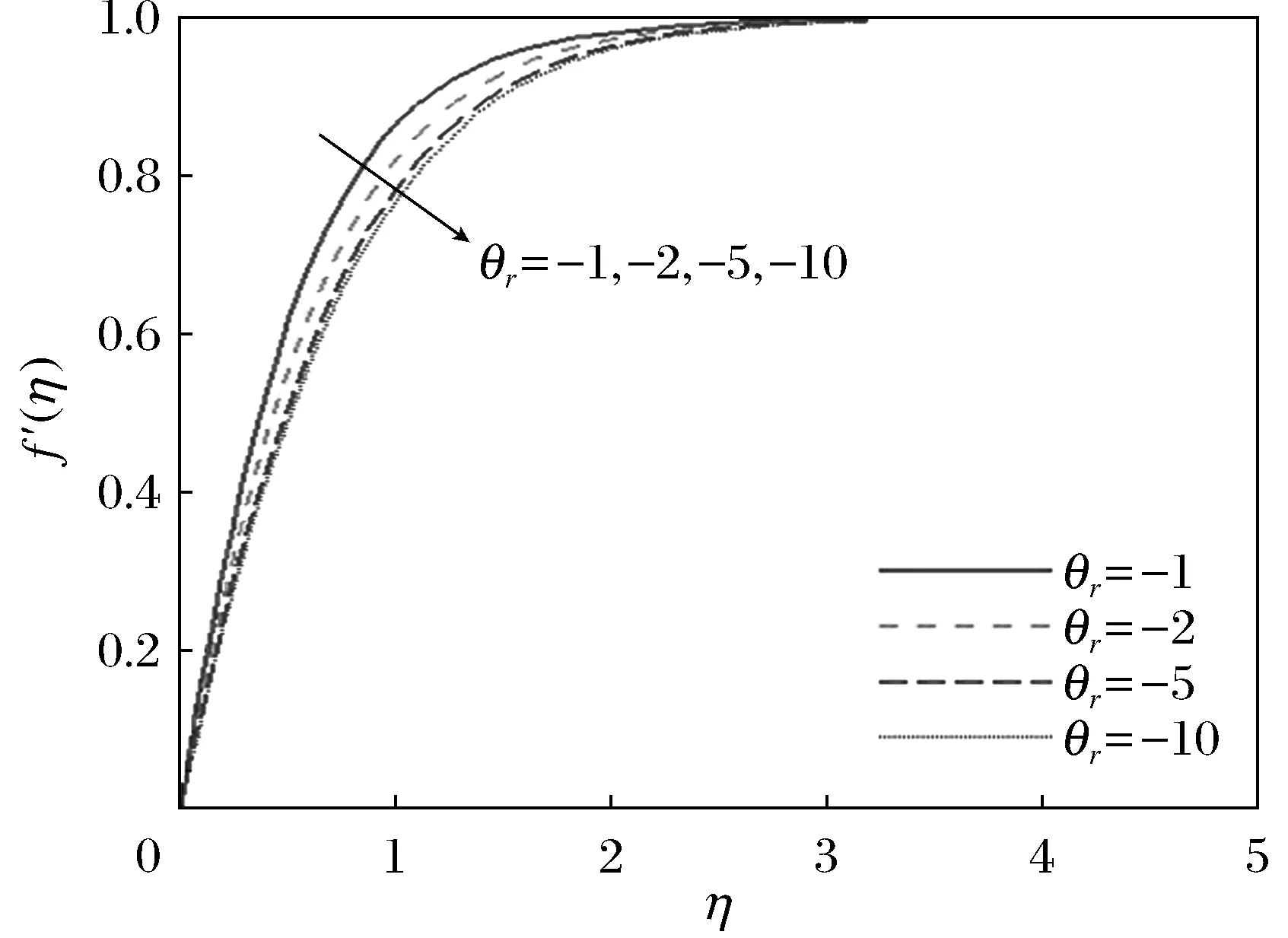
图7 Pr=0.72,β=0.1时,不同θr值对应的f′(η)剖面

图8 Pr=0.72,β=0.1时,不同θr值对应的g′(η)剖面

图9 Pr=0.72,β=0.1时,不同θr值对应的θ(η)剖面

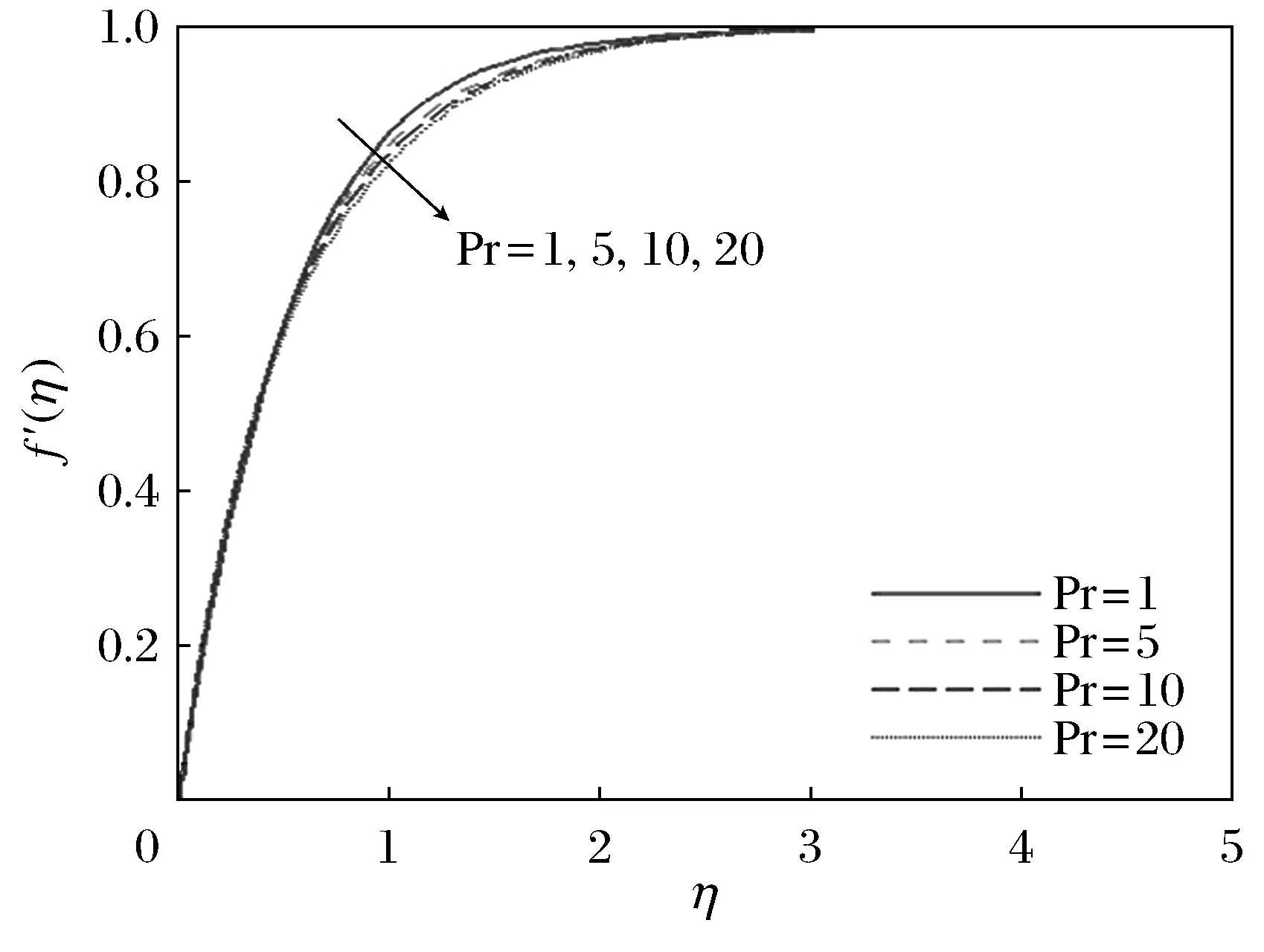
图10 θr=-1,β=0.1时,不同Pr值对应的f′(η)剖面

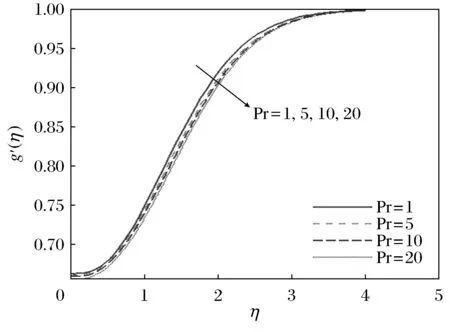
图11 θr=-1,β=0.1时,不同Pr值对应的g′(η)剖面

图12 θr=-1,β=0.1时,不同Pr值对应的θ(η)剖面Fig.12 θ(η) profiles for different values of Pr when θr=-1,β=0.1

从图12也可以发现热边界层厚度随着Pr的增加而减少。这个结果是所期望得到的,因为传热能力会随着Pr的增加而减小,即热边界层厚度将会减少。

3 结 论

本文研究了考虑感应磁场的2维粘性导电流体驻点流问题,详细分析了变粘性系数下流场随磁系数、粘性参数及普朗特数的变化情况。发现速度和感应磁场随着β和-θr的增加而减小,而温度随着β和-θr的增加而增加;速度、感应磁场和温度都随着Pr的增加而减小。

[ 1 ]HIEMENZK.DieGrenzschichtaneinemindengleichförmigenFlüssigkeitsstromeingetauchtengeradenKreiszylinder[J].Dingler’sPolytech, 1911,3326:321-324.

[ 2 ]MAHAPATRATR,GUPTAAS.Magnetohydrodynamicstagnation-pointflowtowardsastretchingsheet[J].ActaMech, 2001,152(1/2/3/4):191-196.

[ 3 ]GROSANT,POPI,REVNICC,etal.Magnetohydrodynamicobliquestagnation-pointflow[J].ActaMech, 2009,44(5):565-572.

[ 4 ]LOKYY,MERKINIJH,POPI.MHDobliquestagnation-pointflowtowardsastretching/shrinkingsurface[J].ActaMech, 2015,50(12):2949-2961.

[ 5 ]MAHAPATRATR,NANDYSK,GUPTAAS.Obliquestagnation-pointflowandheattransfertowardsashrinkingsheetwiththermalradiation[J].ActaMech, 2012,47(6):1325-1335.

[ 6 ]CHIAMTC.Heattransferwithvariableconductivityinastagnation-pointflowtowardsastretchingsheet[J].IntCommunHeatMass, 1996,23(2):239-248.

[ 7 ]ALIFM,NAZARR,ARIFINNM,etal.MHDstagnation-pointflowandheattransfertowardsstretchingsheetwithinducedmagneticfield[J].ApplMathMech, 2011,32(4):409-418.

[ 8 ]SINGHP,TOMARNS,KUMARS.MHDobliquestagnation-pointflowtowardsastretchingsheetwithheattransfer[J].IntJofApplMathandMech, 2010,6(13):94-111.

[ 9 ]DAVIESTV.Themagneto-hydrodynamicboundarylayerinthetwo-dimensionalsteadyflowpastasemi-infiniteflatplateI.Uniformconditionsatinfinite[J].ProcRoySocSerAMathPhysEngSci, 1963,273:496-508.

[10]PRASADKV,VAJRAVELUK,DATTIPS.Theeffectsofvariablefluidpropertiesonthehydro-magneticflowandheattransferoveranon-linearlystretchingsheet[J].IntJThermSci, 2010,49(3):603-610.

[11]HOWARTHL.Onthecalculationofthesteadyflowintheboundarylayernearthesurfaceofacylinderinastream[R].London:Majesty’sStationeryOffice, 1934:1-56.

[12]LIGB,GAOZ.Exactsolutionfortwodimensionalunsteadyobliquestagnationpointflow-Anapplicationofinteractingshearflowstheory[J].ActaAeroDynamicaSinica, 2008,26(S1):83-86.

AnalyticalsolutionsofvariablethermalconductivityonMHDstagnation-ointflow

LI Mingjun, LI Shengnan, LI Guibo

(CollegeofMathematicsandSystemsScience,ShenyangNormalUniversity,Shenyang110034,China)

Thetwo-dimensionalMHDstagnation-pointflowwithvariableviscosityisstudied.TheplateisplacedinthesizeoftherelativelystaticmagneticfieldofH0,theNavier-Stokesequationsarecalculated,whereviscosityisconsideredasafunctionoftemperature.ThegoverningNavier-StokesequationsfortheMHDstagnation-pointflowwithvariableviscositywereobtainedthroughphysicalanalysis.Byusingsimilaritytransformation,thegoverningequationsarefirstlytransformedintotheordinarydifferentialequations(ODEs).Numericallytheeffectsofmagneticstrengthandtemperaturechangestotheskinfrictioncoefficient,heattransfernearthewallandflowfieldcharacteristicsareanalyzed,andthetrendofvelocity,magneticfieldandtemperaturefieldwithdifferentparametersarealsoobtained.

stagnation-pointflow;MHDflow;variableviscosity;similaritytransformation;shootingmethod

2016-08-05。

国家自然科学基金资助项目(11171281); 辽宁省科技厅自然科学基金资助项目(201502065, 201602673)。

李明军(1968-),男,湖南益阳人,沈阳师范大学教授,博士,湘潭大学博士研究生导师。

1673-5862(2017)01-0068-05

O

A

10.3969/j.issn.1673-5862.2017.01.012