侧压对材料有效压缩模量的影响

崔 崧, 陈岚峰, 张治国

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)

侧压对材料有效压缩模量的影响

崔 崧, 陈岚峰, 张治国

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)

损伤力学是固体力学的一个分支,是材料变形与破坏理论的重要组成部分。损伤力学的研究方法有宏观和细观之分,宏观方法更便于工程实际的应用,而细观方法有着更为清晰的物理背景。复杂应力状态下裂纹面间的正应力和剪应力的分析是损伤力学中经常涉及的问题,可以用宏观损伤理论分析侧压条件下裂纹面的闭合应力,从而得到裂纹面间的正应力,然后在弹性力学理论的基础上,利用细观力学分析中的某种平均化方法,推导出脆性和准脆性材料沿裂纹面法线方向的压缩应力-应变本构关系,同时可得到侧压条件下材料的有效压缩模量。计算结果表明,侧压和裂纹面的闭合应力对材料的压缩杨氏模量有一定的影响。由该理论得到的裂纹面间的正应力可知裂纹面间的剪应力,由此可分析考虑摩擦效应的有效剪切模量。

损伤力学; 弹性力学; 侧压; 裂纹面; 杨氏模量

0 引 言

损伤力学是经典固体理论的重要补充和发展,它的研究方法主要有2种,一种是宏观的唯象学方法[1-4],一种是细观分析法[5-8],2种方法各有其优缺点,将宏观和细观相结合的损伤理论是损伤力学今后发展的一个趋势,而且可以较好地解释复杂加载状态材料的力学行为。

含缺陷材料裂纹面间的正应力与剪应力可能会显著影响材料的各项机械性能,其中裂纹面间的正应力不仅与材料的压缩杨氏模量密切相关,而且还影响裂纹面间剪应力的大小,从而影响材料的剪切模量。对于一个含裂纹并且沿裂纹方向受侧压的单元体,先用唯象损伤力学理论可分析出裂纹的闭合应力,再用弹性力学理论并结合细观法的平均化思想,可得到压应力作用下的应力应变本构关系,进而可知沿裂纹面法线方向的有效压缩模量,此结论适用于脆性和准脆性材料。

1 侧压作用下的单元体裂纹面间的正应力

对于裂纹面间的正应力,很多文献处理得都较为简单,例如文献[9]认为当裂纹面法线方向的远场应力为拉应力时,裂纹面间正应力为0,当远场应力为压应力时,裂纹面间正应力值为远场应力值。这种处理方法在复杂载荷状态下可能会有一定误差,对此可作一些改进。

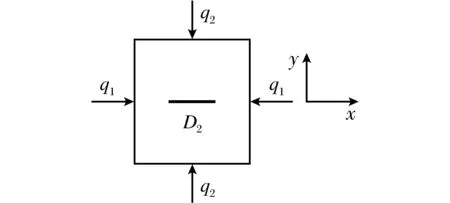
图1 含一条裂纹的单元体Fig.1 Element with one crack

考虑如图1所示的平面应力下含一条裂纹的单元体,裂纹沿x轴。若裂纹张开,则单元体的应力应变本构关系为[10]

(1)

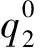
(2)

2 含裂纹单元体压缩本构关系的细观描述

考虑一个如图2所示的内部含一条裂隙的无限大薄板,其中,裂隙沿x轴方向,长度为2a。薄板远端在x轴方向作用有固定均布压力q1,在此条件下在y轴方向的远端施加逐渐增加的压应力q2。在薄板上以裂纹为中心截取一单元体,其长度为2l,高度为2h,如图3所示。

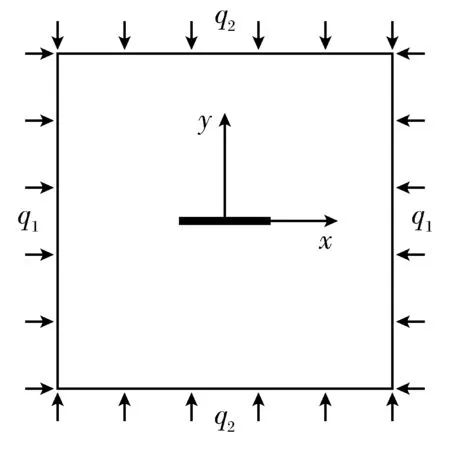
图2 远端受双轴压缩载荷的薄板

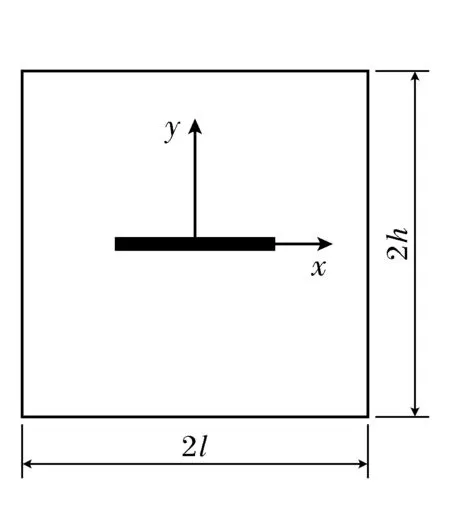
图3 中心含裂纹的单元体

薄板上各点的位移可由弹性理论中的复变函数表示式[11-12]

(3)

求出,其中φ1(z)、ψ1(z)为变量z=x+iy的复变函数。

当q2≥μq1时,由式(2)可知裂纹面有正应力q3,且q3=q2-μq1,薄板在应力边界条件q2、q3下式(3)中的复变函数φ1(z)、ψ1(z)的表达式[11]的叠加形式为

(4)

将式(4)代入式(3),可以得出在各点(x,y)的位移u和v,其中沿y轴方向的位移可简化为

(5)

其中函数f2(x,y)只是点坐标的函数,与薄板所加载荷无关,其量纲是长度单位。利用式(5),可知图3所示单元体边界y=h上各点位移v(x,h)=μq1·f2(x,h)/E+q2·h/E,该边界的平均位移可写为

由上式,可得单元体沿y轴方向的总体线应变

利用上式,可以推导出有侧压q1前提下单元体压缩应力应变本构关系为

(6)

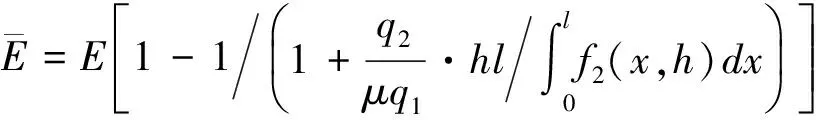
当q2<μq1时,裂纹面张开,式(6)则变为

(7)

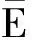
图/E随q2变化的关系曲线

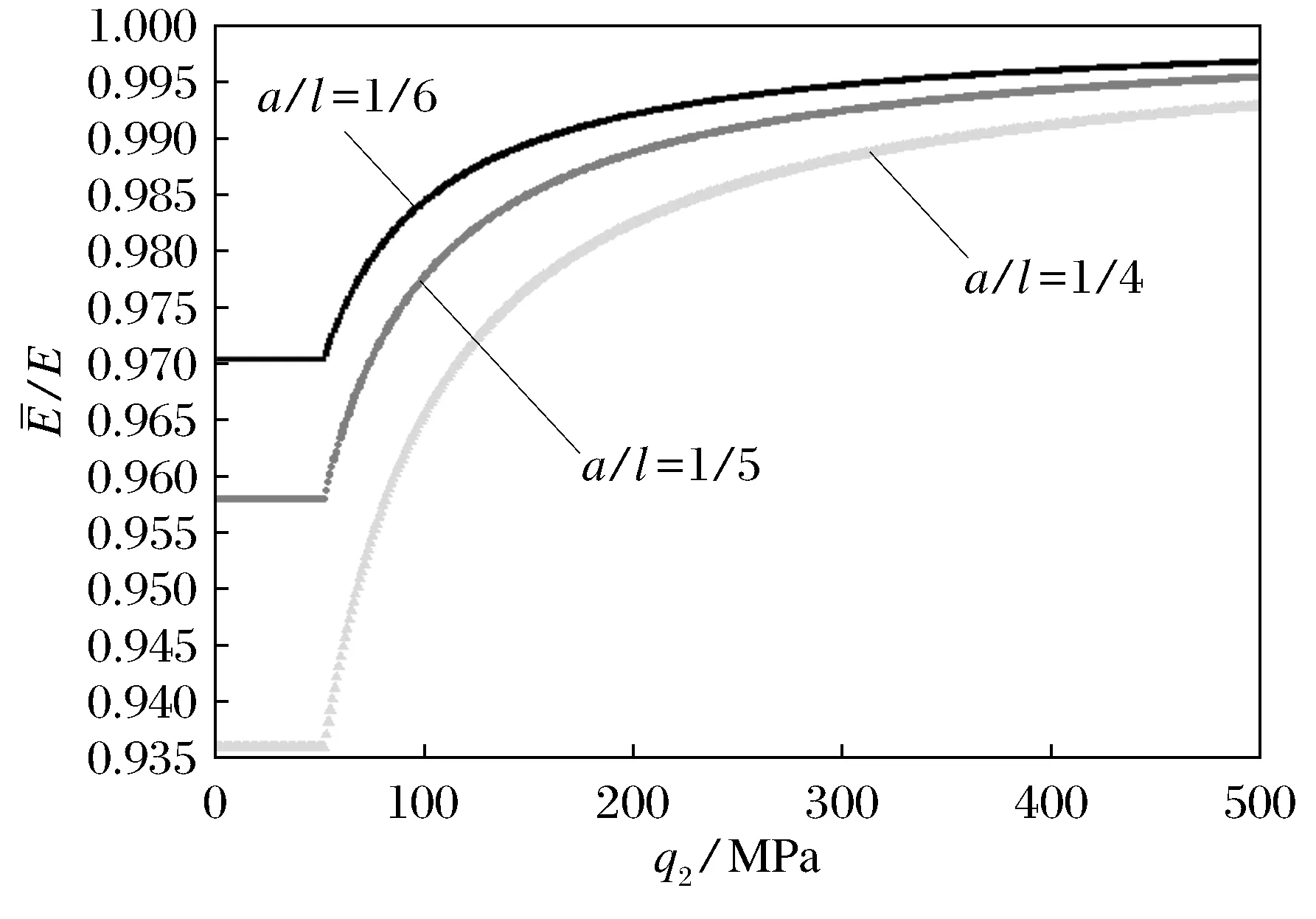
图5 不同裂纹尺寸下/E与q2的关系曲线

3 结 语

利用弹性力学理论和细观力学分析方法,得到了有侧压条件下的脆性材料有效压缩模量的公式,其中裂纹面间正应力在表达式中起着重要的作用。该理论不仅可以分析和计算材料的有效压缩模量,还可用于有关裂纹面间摩擦效应方面的研究[14-15],从而可分析复杂加载条件下有着任意分布裂纹材料的各项有效弹性模量。

[ 1 ]KRAJCINOVIC D,FONSEKA G U. The continuous damage theory of brittle materials[J]. J Appl Mech, 1981,48(4):809-824.

[ 2 ]TALREJA R. Damage development in composites: Mechanics and model[J]. J strain Anal Eng, 1989,24(4):215-222.

[ 3 ]CHOW C L, WANG J. An anisotropic theory of elasticity for continuum damage mechanics[J].Int J Fract, 1987,33(1):3-16.

[ 4 ]SWOBODA G,YANG Qiang. An energy-based damage model of geomaterials (part 1 and part 2)[J]. Int J Sol S, 1999,36(12):1719-1755.

[ 5 ]BENVENSITE Y. On the Mori-Tanaka’s method in cracked solids[J]. Mech Res Comm, 1986,13(4):193-201.

[ 6 ]HUANG Y, HU K, CHANDRA A. A generalized self-consistent mechanics method for microcracked solids[J]. J Mech Phys Solids, 1994,42(8):1273-1291.

[ 7 ]冯西桥. 脆性材料的细观损伤理论和损伤结构的安定分析[D]. 北京:清华大学, 1995.

[ 8 ]BASISTA M, GROSS D. The sliding crack model of brittle deformation: an internal variable approach[J]. Int J Sol S, 1998,35(5):487-509.

[ 9 ]HORII H, NEMAT-NASSER S. Overall moduli of solids with microcracks: load-induced anisotropy[J]. J Mech Phys Solids, 1983,31(2):155-171.

[10]崔崧,陈岚峰. 拉伸损伤细观机理的弹性力学分析[J]. 沈阳师范大学学报(自然科学版), 2013,31(4):451-454.

[11]徐芝纶. 弹性力学:上册[M]. 4版. 北京:高等教育出版社, 2006.

[12]陆明万,罗学富. 弹性理论基础:下册[M]. 2版.北京:清华大学出版社, 2001.

[13]蔡美峰. 岩石力学与工程[M]. 北京:科学出版社, 2002.

[14]DRAGON A, HALM D, DESOYER T. Anisotropic damage in quasi-brittle solids: modeling, computational issues and applications[J]. Comput Meth, 2000,183(3/4):331-352.

[15]崔崧,吕嫣. 裂纹方向对剪切损伤模量的影响[J]. 沈阳师范大学学报(自然科学版), 2015,33(4):459-462.

Influence of lateral pressure on effective compression modulus of materials

CUISong,CHENLanfeng,ZHANGZhiguo

(College of Physical Science and Technology, Shenyang Normal University, Shenyang 110034, China)

Damage mechanics is a branch of solid mechanics, which is an important part of the theory of deformation and failure of materials. There are two main research methods: macro and meso view, the former is more convenient for engineering application, and the latter has a more clearly physical background. The analysis of the normal stress and the shear stress between the crack surfaces in complex stress state is often involved in damage mechanics. Using the macro damage theory to analyze the crack closure stress under lateral pressure, the normal stress between the crack surfaces can be obtained, and then based on the theory of elasticity, using some averaging method of mesomechanics, the stress-strain constitutive relation of compression in the normal direction for brittle solids can be deduced, and simultaneously get the effective compression modulus under the lateral pressure. The calculate results show that the lateral pressure and the crack closure stress can have some effect on the compressive Young’s modulus. The shear stress between the crack surfaces can be obtained by this theory. The effective shear modulus can be analyzed through considering the frictional effect.

damage mechanics; elasticity; lateral pressure; crack surface; Young’s modulus

2016-08-14。

辽宁省教育厅科学研究一般项目(L2014442)。

崔 崧(1969-),男(满族),辽宁本溪人,沈阳师范大学副教授,博士。

1673-5862(2017)01-0039-04

O343.1

A

10.3969/ j.issn.1673-5862.2017.01.007