民用飞机着陆垂直加速度标准的优化模型
2017-02-27赵新斌
赵新斌, 李 斌
(中国民航科学技术研究院 航空安全研究所, 北京 100028)
民用飞机着陆垂直加速度标准的优化模型
赵新斌, 李 斌
(中国民航科学技术研究院 航空安全研究所, 北京 100028)
飞行品质监控是分析查找原因、消除隐患、确保飞行安全的有效手段。为了避免人为主观因素对飞行品质监控项目标准制定的影响,提高监控项目预测的准确性,基于着陆垂直加速度的截尾正态性和风险度量理论,提出了民用飞机着陆垂直加速度标准的诊断模型,该模型通过风险极大化的思想,得到了着陆垂直加速度的次优监控标准。通过对某航空公司的数据进行数值试验,给出了某高原机场和某普通机场的着陆垂直加速度超限标准和一些相关结论,结果表明,监控项目标准具有动态性,该诊断模型是合理有效的,除了用来诊断着陆垂直加速度,此诊断模型还可以运用到满足截尾正态分布的其他参数上。
民用航空安全; 重着陆; 着陆垂直加速度; 监控标准; 截尾正态分布
0 引 言
民用航空事故具有发生概率小和死亡率高的特点,对一个国家的政治和经济都有着深远的影响,因此,“航空安全”是民用航空领域的重要指标[1]。民航不安全事件统计表明,着陆阶段是民用飞机飞行中最危险的阶段,不安全事件的发生率明显高于其他飞行阶段[2-3]。重着陆是其中一类发生频率较高的不安全事件,2006—2015年我国民航共发生重着陆事件482起(一般事故征候8起,严重事故征候1起),约占着陆阶段不安全事件总数的24%。在现阶段实施的飞行品质监控项目中,主要是通过检测飞机重心的垂直加速度是否超过监控标准来判定重着陆是否发生。因此,为了提高飞行品质监控水平和飞行员的训练水平,给出更加合理的垂直加速度监控标准就显得尤为重要。
1 重着陆机理
重着陆在飞行界是一个约定俗称的概念。波音公司将重着陆定义为:飞机着陆时垂直加速度超过规定极限值或者垂直方向上的速度超过规定值[4]。重着陆的发生会使飞机的结构,特别是起落架、机翼等部件承受较大的载荷,对机体造成损伤,给航空公司带来巨大的经济损失,情况严重时会引发灾难性的后果,对旅客的生命安全造成威胁,而这些损伤目视往往很难发现。通过对QAR数据进行分析,制定特定机型合理的垂直加速度监控标准,才能实现对飞行品质监控的优化,从而规范飞行员的训练,有效地判别是否发生重着陆,防止重着陆事件的发生。
由于重着陆事件具有频发性,为了有效地诊断和预防此类事件的发生,对重着陆事件的研究引起了国内研究者的高度关注。基于飞行QAR数据,采用数据挖掘的方法对重着陆进行诊断和预测是目前的一个研究重点。曹海鹏等[5]采用1个输入层、1个输出层和1个隐含层的3层神经网络的方法来建立模型,实现对重着陆事件的准确判断;聂磊等[6]首先将对重着陆事件的预测转换成一个二分类问题(第1类为发生重着陆,第2类为未发生重着陆),然后采用支持向量机的方法来实现对重着陆事件的预测;王旭辉等[7]则是根据飞机接地阶段重着陆事件的形成机制,分别建立了翼根载荷与起落架载荷的受力模型,并基于“1对1(One-against-one)”思想,采用支持向量机来解决由正常着陆、翼根载荷引发的重着陆和起落架载荷引发的重着陆三分类问题,以此实现对重着陆事件的预测;许桂梅[8]通过采用支持持向量机的拓展模型----最小二乘支持向量机来建立飞机重着陆诊断模型,不但节省了大量的计算时间,而且提高了飞机重着陆事件判断的准确性。
重着陆事件诊断模型的建立通常基于如下5个参数:垂直加速度(vertical acceleration)、下降率(inertial vertical speed)、侧向加速度(lateral acceleration)、横滚角(roll angle)和俯仰角变化率(pitch-angle rate),其中垂直加速度最能直接反映重着陆事件的发生与否,对诊断重着陆事件起着举足轻重的作用。通常情况下,航空公司是根据垂直加速度是否超限来判断飞机是否发生重着陆,这种方法容易受到人为主观性的影响,且建模的角度比较单一,因此,该方法对重着陆事件的判断往往不够准确。由此不难看出,为了提高重着陆事件的预测准确性,以此实现飞行品质监控的优化和飞行员训练水平的提高,必须制定合理的垂直加速度监控和训练标准,而通过对飞行QAR数据的分析和挖掘是得到合理垂直加速度监控和训练标准的有效手段。
本文基于垂直加速度的截尾正态性,从数据分布特征的角度,利用极大化风险(损失)的思想,建立了着陆垂直加速度的监控和训练标准的预测模型。该方法摆脱了传统方法的束缚,得到的垂直加速度监控和训练标准更加客观。
2 预备知识
2.1 正态分布与截尾正态分析
首先介绍正态分布的定义,以及其密度函数和分布函数[9]。
若随机变量X的概率密度函数为
(1)

图1 正态分布概率密度函数Fig.1 Probability density function of Normal Distribution
则称X服从正态分布,称X为正态变量,记作X~N(μ,σ2),其中参数-∞<μ<+∞,σ>0。均值μ=0,标准差σ=2的概率密度函数p(x)的图形如图1所示。p(x)是1条钟形曲线,中间高、两边低、左右关于μ对称,μ是正态分布的中心,且在x=μ附近取值的可能性大,在两侧取值的可能性小。μ±σ是该曲线的拐点。根据正态分布的概率密度函数p(x)可得到正态分布N(μ,σ2)的分布函数
(2)
由于正态分布是一种常见且重要的分布,因此,人们在实际使用统计分析时,总是乐于正态假设,但假设是否成立,就需要进行正态性检验。目前,最常用的正态性检验方法有以下几种[10-11]:正态概率纸法、χ2拟合优度检验法、W检验和D检验法、偏度检验与峰度检验法、Liffifors检验法、正态概率累计分布图法,以及最为简便的经验法。本文采用的正态性检验方法为经验法:用样本中位数M与均值μ的比值和均值μ与标准差σ的关系来进行判断,而上述关系反映的恰是样本概率密度曲线的峰形和峰态。若下述2个关系式
(3)
成立,则可认为样本大致为正态分布。
正态分布是关于均值对称的,其随机变量的取值范围是(-∞,+∞)。但是,在实际的工程实验中,许多试验数据只有正值而没有负值,严格说并不服从正态分布。为了使计算结果更加符合实际情况,需要将截尾正态分布作为其近似分布。与正态分布的取值范围相比,截尾正态分布的取值范围
(4)
是比较小的。由于截尾正态分布是将正态分布随机变量限制在一个区间内得到的新概率分布,因此,截尾正态分布与正态分布的概率密度函数与分布函数具有如下关系[12]:
(5)
(6)
2.2 风险度量
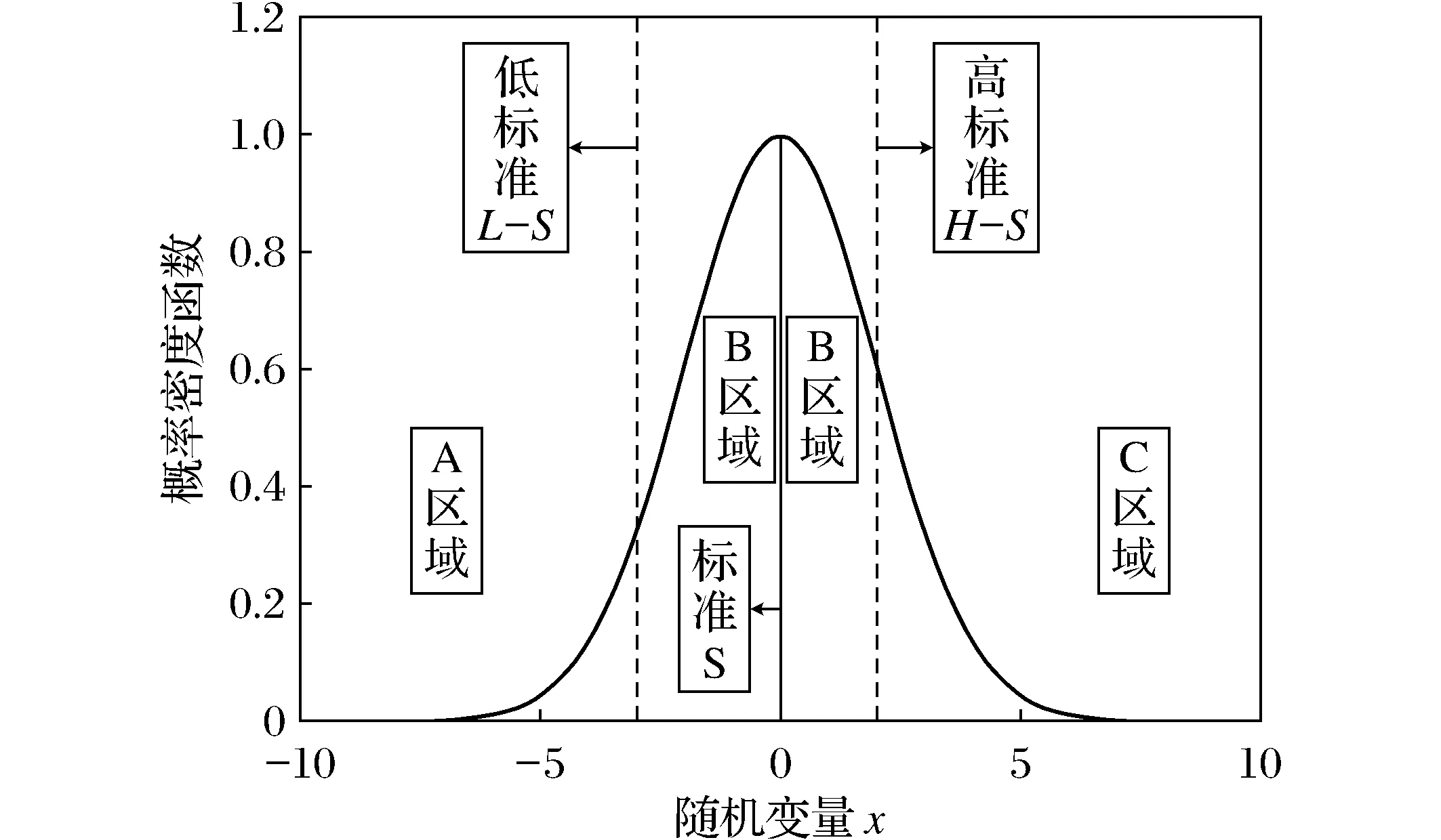
图2 风险区间Fig.2 The zone of the risk
一个标准的制定总是伴有风险的,不同的标准决定了风险的高低,而目的是将发生的风险降到最低。在度量一个标准的风险时,首先需要确定的是度量风险的区间。
首先引进低标准线L_S(low-standardline)、标准线S(standardline)和高标准线H_S(high-standardline)的概念。所谓的L_S和H_S指的是事件发生所允许的最低限和最高限,而所谓标准线是事件发生的理想值,如图2所示:L_S、S和H_S将概率密度函数曲线下的区域分成A、B和C这3个区域。由于A区域和C区域中x的值分别小于L_S和大于H_S,因此,较B区域而言,要加大对A区域和C区域的风险度量,而风险的度量大小主要依赖于风险函数。本文采用的风险函数主要是距离度量函数。
3 着陆垂直加速度的截尾正态性和标准诊断模型
本节基于风险极大化的思想,建立了着陆垂直加速度标准的诊断模型,该模型既能用来检验制定标准是否合理,也能够为标准的制定提供一定的参考依据。以某机型的10 000余个QAR数据作为研究数据集,首先对着陆垂直加速度的正态性进行验证,进而通过数据本身的特征得到其满足截尾正态分布。
3.1 着陆垂直加速度的截尾正态性
对研究数据集中的着陆垂直加速度的数据进行统计分析后,得到其均值μ=1.156 4,标准差σ=0.076 6,中位数M=1.140 6,然后采用正态性检验的经验法来对其正态性进行验证。经计算
(7)

(8)
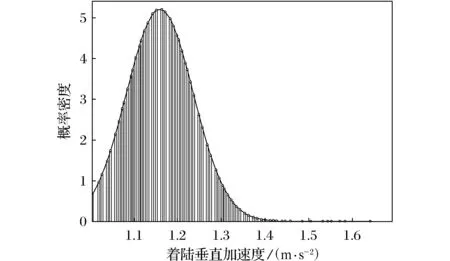
图3 着陆垂直加速度数据分布Fig.3 Distribution of landing vertical acceleration
式(7)和式(8)均满足经验法的式(3),由此可以判断这些样本的着陆垂直加速度的数据大致为正态分布。
通过观察研究数据集中的着陆垂直加速度的概率累计分布图(见图3),容易得到着陆垂直加速度的分布具有如下特征:
1) 着陆垂直加速度的数据只有正值而没有负值;
2) 着陆垂直加速度的数据取值范围是有界区间(4),而不是无界区间(-∞,+∞)。
因此,严格地说着陆垂直加速度并不服从正态分布,而是截尾正态分布。
3.2 着陆垂直加速度标准的诊断模型
本节主要给出着陆垂直加速度标准的诊断模型,利用这个模型可以实现诊断着陆垂直加速度监控标准是够合理。首先,给出衡量着陆垂直加速度风险的区间,如图4所示。低标准线L_S和高标准线H_S将概率密度函数曲线下的区域分成B和C这2个区域,由于着陆垂直加速度的取值均大于等于1,因此,在图4中不存在A区域。在中国民用航空局飞行标准司发布的咨询通告《飞行品质监控(FOQA)实施与管理》[13]中,空客系列飞机的着陆垂直加速度的超限值是1.6,即飞机的着陆垂直加速度大于1.6时就会触发着陆垂直过载大这类超限事件;而对于正常的着陆,接地瞬间,其理想状况应该是升力约等于飞机的重力,着陆垂直加速度接近1[14]。因此,在本文中,分别设置高标准线H_S和低标准线L_S的初始值为1.6和1。也就是说,B和C这2个区域的着陆垂直加速度的取值区间分别是1≤gB≤1.6和1.6 图4 着陆垂直加速度风险区间Fig.4 The zone of landing vertical acceleration risk 以上内容给定了衡量着陆垂直加速度风险的区间,下面主要介绍采用何种风险(损失)函数来度量B和C这2个区域的风险(损失)。不难得到,C区域的风险显然要高于B区域。为了便于区别,记B区域的左右部分分别为B-L和B-R,通过观察图4能够看出,B-L区域和B-R区域关于标准值S并不是左右对称的,因此,需要对B-L区域和B-R区域采用不同的风险函数。综上所述, B-L、B-R和C这3个区域需要采用3种不同的风险函数来进行度量。 基于图4所示的数据分布,C、B-L和B-R这3个区域的风险函数分别为一次风险函数 (9) 和二次风险函数 (10) (11) 其中:S为标准值;kC、kB-L和kB-R分别为这3个风险函数的风险系数。 于是,C、B-L和B-R这3个区域的风险分别为 (12) (13) (14) 若θ1>L_S,则式(12)需写成以下形式: (15) 其中θ1和θ2如式(4)所示。 然后将截尾正态分布的概率密度函数(5)代入到式(13)、式(14)和式(15)中得 (16) (17) (18) 其中, 这里φ(·)和Φ(·)分别是标准正态分布N(0,1)的概率密度函数和分布函数。 基于风险极大化的思想,通过如下着陆垂直加速度标准的诊断模型 (19) 来求得使B-R区域和C区域风险都较大的次优解H_S*。需要强调的是,由于不存在A区域,因此,诊断模型不存在变量L_S,这也就决定了B-L的风险在整个算法过程中是不变的,在模型(19)中不存在风险LB-L。 下面给出着陆垂直加速度标准诊断的具体算法。 高标准H_S的设置可以用来制定飞行品质监控中的超限事件的超限标准,因此,表1中的算法可以用来诊断制定的超限标准是否合理。从而使得制定的超限标准来源于真正的飞行QAR数据,打破了人为观念的束缚,避免了人为制定超限标准所产生的不合理性。 表1 着陆垂直加速度标准诊断算法 本节从第3节中的研究数据集中挑出1个高原机场和1个普通机场的数据,基于这些数据,采用表1中的算法,给出了适合这2个机场的着陆垂直加速度的超限标准。 这2个机场的相关数据信息如表2所示。 表2 数据详情 将这2个机场的数据经过表1中的算法计算后,得到的结果如图5所示。 (a)—高原机场; (b)—普通机场 结果表明,这个高原机场和普通机场的着陆垂直加速度的监控标准分别是1.33和1.312,发生重着陆事件的概率分别为7.91%和2.12%。由于高原机场特殊的地理环境和气候环境,在高原机场发生重着陆的概率要高于普通机场发生重着陆的概率。从表2容易看出,与普通机场相比,在样本数量较小的前提下,高原机场着陆垂直加速度的均值和方差都较高,这说明飞机在高原机场产生的着陆垂直加速度平均要高于普通机场。因此,只有在着陆垂直加速度比较大时,才算是发生了超限事件,才有预警的必要;而与高原机场相反,普通机场的超限标准要低,这样才能作为超限事件及时发现着陆垂直加速度高于平均水平的飞机,及时采取措施,避免飞行员继续采用不当的操作导致着陆垂直加速度大事故征候的发生,而本节数值实验得到的结果,也有效地验证了这些结论。 通过上述实验, 对监控标准的制定应该具有一定的区分性和针对性, 统一的标准可能并不是最理想的。 人为的制定标准难免主观性对结果的影响, 通过对飞行数据进行数据分析得到的标准才是合理的。 随着民用航空业的不断发展,“民航安全”已经被提升到了一个空前的战略高度,如何提高和保障民航安全是目前民航界的首要任务。飞行品质监控作为提高和保障民航安全的重要手段,受到了民航相关单位的高度重视,取得了快速的发展,但也存在一些问题。 飞行品质监控项目中的监控标准往往都是人为制定的,这就无法避免人为主观性对标准的影响。为了避免不合理标准对事件的误判,基于飞行QAR数据中的着陆垂直加速度,给出了诊断其标准的模型和算法,并通过飞行QAR数据实验验证了模型的合理性,得到的相关结论如下: 1) 传统的人为制定监控标准具有很强的人为主观性,无法适用所有情形,容易出现对事件的误判; 2) 监控标准应该具有动态性,以此满足不同机型、不同机场、不同环境下的监控要求。 本文对民航告警的展望主要包括以下3点: 1) 将模型和算法运用到其他符合截尾正态分布的参数标准的诊断上; 2) 通过“分位数”来制定监控项目标准,无需考虑参数的分布; 3) 将机型、机场和环境等因素进行结合,诊断多因素下的监控标准。 [ 1 ]TODDJC.Aviationsafety:U.S.effortstoimplementflightoperationsqualityassurance[J].FlightSafetyDigest, 1998,17:7-9. [ 2 ]SHAPPELLS,DETWILERC,HOLCOMBK,etal.Humanerrorandcommercialaviationaccidents:ananalysisusingthehumanfactorsanalysisandclassificationsystem[J].HumanFactors, 2007,49(2):227-242. [ 3 ]BoeingCommercialAirplanes.Statisticalsummaryofcommercialjetairplaneaccidentsworldwideoperations1959-2012[R].Seattle,WA:BoeingCommercialAirplanes, 2013. [ 4 ]许桂梅,黄圣国. 基于多核支持向量机的飞机重着陆诊断[J]. 计算机工程, 2011,37(10):157-159. [ 5 ]曹海鹏,舒平,黄圣国. 基于神经网络的民用飞机重着陆诊断技术研究[J]. 计算机测量与控制, 2008,16(7):906-908. [ 6 ]聂磊,黄圣国,舒平,等. 基于支持向量机(SVM)的民用飞机重着陆智能诊断研究[J]. 中国安全科学学报, 2009,19(7):149-153. [ 7 ]王旭辉,舒平,黄圣国. 民用飞行器重着陆事件决策系统研究[J]. 中国安全科学学报, 2010,20(2):116-120. [ 8 ]许桂梅,黄圣国. 应用LS-SVM的飞机重着陆诊断[J]. 系统工程理论与实践, 2010,30(4):763-768. [ 9 ]茆诗松,程依明,濮晓龙. 概率论与数理统计[M]. 北京:高等教育出版社, 2004:102-103. [10]周洪伟. 正态性检验的几种常用的方法[J]. 南京晓庄学院学报, 2012(3):13-18. [11]周雁翎,张琼雄,张练. 粤西降水量的分布特征及正态分布检验[C]∥中国气象学会2007年年会天气预报预警和影响评估技术分会场论文集. 北京:中国气象学会, 2007:727-731. [12]田薇,李晓毅,付志慧. 在R语言中实现Bayes方法对logistic的回归分析[J]. 沈阳师范大学学报(自然科学版), 2016,34(3):305-310. [13]中国民用航空局飞行标准司. 飞行品质监(FOQA)实施与管理:AC-121/135-FS-2012-45R1[S]. 北京:中国民用航空局, 2015:17-21. [14]舒平,王旭辉,黄圣国,等. 民用飞机重着陆响应及诊断研究[J]. 中国制造业信息化, 2009,38(15):68 -72. [15]董欢欢. 非对称平方损失函数下的贝叶斯回归[D]. 杭州:浙江大学, 2014:4-16. [16]李秋洁,赵亚琴,顾洲. 代价敏感学习中的损失函数设计[J]. 控制理论与应用, 2015,32(5):689-694. Optimization model of civil aircraft landing vertical acceleration standard ZHAOXinbin,LIBin (Aviation Safety Institute, China Academy of Civil Aviation Science and Technology, Beijing 100028, China) Flight operational quality assurance is an effective means to analyze the causes, eliminate hidden dangers and ensure flight safety. In order to avoid the influence of subjective factors on the overrun standards, and improve the forecasting accuracy of overrun event, based on the truncated normal property of landing vertical acceleration and risk measure theory, the standard diagnostic model of civilian aircraft landing vertical acceleration is proposed, the model obtains the suboptimal standard by the idea of maximum risk. According to the experiments of an airline’s flight data, the overrun standards of landing vertical acceleration and some relevant conclusions of a plateau airport and a normal airport are presented, the results show that the overrun standards are dynamic and the diagnostic model of this paper is reasonable and effective. In addition to landing vertical acceleration, this diagnostic model can also be applied to other parameters, which meet the truncated normal distribution. civil aviation safety; hard landing; landing vertical acceleration; quality standards; truncated normal distribution 2016-10-10。 国家自然科学基金民航联合基金资助项目(U1533120). 赵新斌(1986-),男,山东即墨人,中国民航科学技术研究院助理研究员,博士. 1673-5862(2017)01-0061-07 O224; X928.03; V19 A 10.3969/ j.issn.1673-5862.2017.01.011

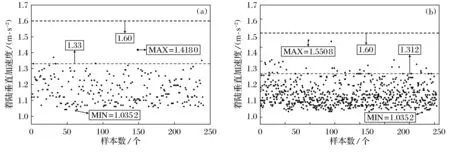
4 数值试验

5 总结与展望
