带有时滞和非线性扰动的中立系统的H∞滤波设计

党胜超, 苏亚坤

(1. 渤海大学 数理学院, 辽宁 锦州 121013; 2. 渤海大学 基础教研部, 辽宁 锦州 121013)

带有时滞和非线性扰动的中立系统的H∞滤波设计

党胜超1, 苏亚坤2

(1. 渤海大学 数理学院, 辽宁 锦州 121013; 2. 渤海大学 基础教研部, 辽宁 锦州 121013)

主要讨论带有混合时滞和非线性扰动的不确定中立型系统的H∞滤波设计问题。基于带有混合时滞和非线性扰动,构造了新颖的李雅普诺夫泛函,继而得到了一个新的中立型系统鲁棒稳定的延迟相关条件。通过采用线性矩阵不等式、Lyapunov稳定性理论及凸组合方法获得了具有更小保守性的结果。在满足H∞性能指标条件下,提出了一些新的滤波器存在的充分条件,使得滤波误差系统是渐近稳定的。为了方便使用MATLAB软件解答,将结果用线性矩阵不等式的形式给出,利用LMI工具箱进行求解,最后得到相应数据。和已有的文献相比,该方法得到的判据具有较小保守性。最后通过数值例子验证了该方法的有效性和优越性。

中立型系统; 不确定项;H∞滤波; 依赖延迟; 非线性扰动; 线性矩阵不等式

时滞可以是已知的或者未知的,也可能是定常的或时变的,事实证明时滞的存在往往使系统不稳定和性能变差。一些控制系统中不仅状态中有时滞,状态的导数中也有时滞,这类动态系统称为中立型时滞系统。基于其复杂性,人们主要关注其稳定性研究、鲁棒控制和H∞控制,在时滞系统的滤波设计方面关注相对较少,只是近几年才出现一些研究成果[1-4]。

本文针对带有混合时变时滞和非线性扰动的不确定线性中立型系统,讨论了其稳定性和鲁棒H∞滤波器的设计问题,利用Lyapunov稳定性理论[5],构造合适的Lyapunov泛函[6-7],用线性矩阵不等式[8]、凸组合等方法设计一个H∞滤波器,得到了滤波器存在的充分条件,并把控制器的设计问题转化为线性矩阵不等式可解性问题,最终通过求解线性矩阵不等式来获得满足要求的滤波器。文章最后,通过数值例子来验证本文介绍的方法的有效性。

1 问题描述

考虑带有不确定项的混合时滞和非线性扰动的线性中立型系统:

(1)

式中:x(t)∈Rn表示系统状态变量;y(t)∈Rr表示可测输出变量;z(t)∈Rq表示需要估计的信号向量;w(t)∈Rm为扰动信号且w(t)∈l2(0,+∞);A,A1,A2,K1,K2,B,B1,B2,C,C1,C2是已知的具有适当维数的常数矩阵;f1(x(t),t)∈Rn,f2(x(t-d(t)),t)∈Rn是对于以下2项x(t),x(t-d(t))的未知干扰项;且‖f1(x(t),t)‖≤σ‖x(t)‖,‖f2(x(t-d(t)),t)‖≤ζ‖x(t-d(t))‖;d(t)和h(t)代表时变时滞,且满足如下不等式:

ΔA0(t),ΔA1(t)表示具有时变特征的不确定参数,假设它们范数有界,且满足如下关系式:

式中:H,G1,G2是具有适当维数的常数矩阵;F(t)是一个具有Lebesgue可测元的未知函数矩阵,且满足不等式FT(t)F(t)≤I。

对于上述系统(1)的动态模型可以表示为

(2)

式中:Ad∈Rn×n;Bd∈Rn×r;Cd∈Rp×n和Dd∈Rp×r是滤波参数。

(3)

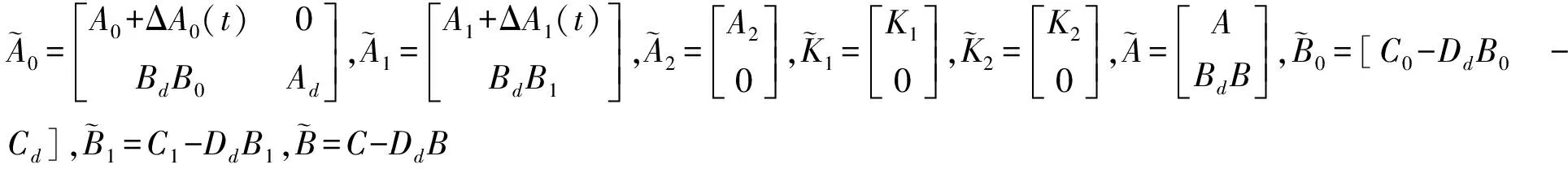
系统(1)的H∞滤波问题就是:设计一个形如(2)的滤波器,使得当w(t)=0时式(3)在平衡点ζ(t)=0处是鲁棒渐近稳定的。对给定常数γ>0,在零初始条件下,当l>0,w(t)∈l2[0,∞)时,满足如下H∞性能指标:

在引入主要结论前,先给出2个引理。

引理1 对于任意向量h(t)≥0和正定矩阵Q,以及适当维数的自由权矩阵W,M,有下式成立:

引理2 假设A,D,S,F(t),W是具有适当维数的实矩阵,其中W>0,F(t)满足不等式F(t)TF(t)≤I,于是下列不等式成立:

1) 对于任意的ε>0和向量x,y∈Rn,总有

2xTDF(t)Sy≤ε-1xTDDTx+εyTSTSy

2) 对于任意的ε>0,使得W-εDDT>0,总有

2 H∞滤波现象分析

首先给出系统(1)H∞滤波存在的充分条件,结论见定理。

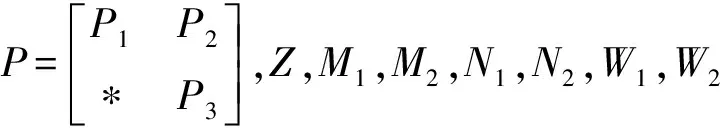
式中,

证明 首先构造如下Lyapunov-Krasovskii泛函:

其中,

对以上泛函求导,得到下列式子:

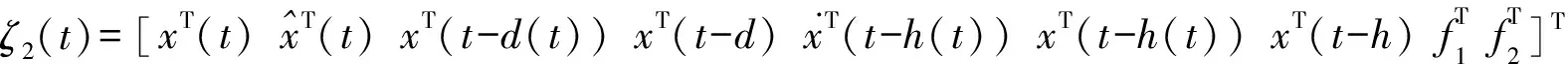
(4)

(5)

由引理1得到

(6)

(7)

(8)

(9)

另外假设

(10)

对于泛函导数中的不确定项:

(11)

(12)

(13)

(14)

由引理2

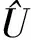
式中,

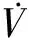
(15)

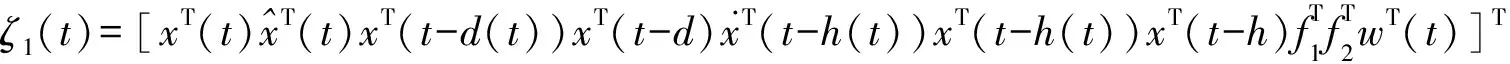
3 滤波设计

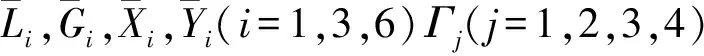
式(2)中的滤波参数设计如下:

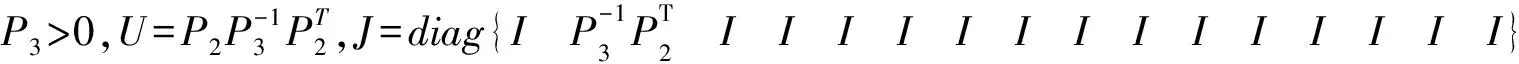
与滤波(2)对比,滤波参数得以确定。

4 仿真例子

例 考虑非线性中立型系统式(1),其系数矩阵为

由定理通过计算可得,在给定的系数矩阵下,性能指标γ的最小值为3.054 8,参数矩阵如下:

5 结 论

本文研究了带有混合时滞和非线性扰动的不确定的中立型系统的H∞滤波设计问题,利用Lyapunov稳定性理论和线性矩阵不等式,在满足性能指标下,对滤波误差系统渐近稳定给出了一些新的依赖延迟充分条件,并且还介绍了凸组合的方法。数值例子验证了本文方法的有效性。

[1]ZHANG Dan, YU Li.H∞filtering for linear neutral systems with mixed time-varying delays and nonlinear perturbations[J]. Journal of the Franklin Institute, 2010,34(7):1374-1390.

[2]苏亚坤,王焕清,滕明岩. 基于T-S模糊模型的非线性系统的控制与滤波设计[M]. 沈阳:辽宁科技出版社, 2014.

[3]ELSAYED, GRIMBLE M J. A new approach toH∞design of optimal digital filters[J]. IMAJ of Math Control and Information,1989,26(8):233-251.

[4]GAO Huijun, WANG Changhong. Delay-dependent robustH∞andL2-L∞filtering for a class of uncertain nonlinear time-delay systems[J]. IEEE Trainsactions on Automatic Control, 2003,48(9):1661-1666.

[5]XU S, LAM J. Improved delay-dependent stability criteria for time-delay systems[J]. IEEE Transactions on Automatica Control, 2005,50(3):384-387.

[6]WU Min,HE Yong,SHE Jinhua. New delay-dependent stability criteria and stabilizing method for neutral systems[J]. IEEE Transactions on Automatic Control, 2005,49(12):2266-2271.

[7]SOUZA F O, PALLARES R M, BARBOSA K A. New improved delay-dependentH∞filter design for uncertain neutral systems[J]. IET Control Appl, 2008,32(2):1033-1043.

[8]PINJAI S, MUKDASAI K. New delay-dependent robust exponential stability criteria of LPD neutral systems with mixed time-varying delays and nonlinear perturbations[J]. IEEE Journal of Applied Mathematics, 2013,27(10):1-18.

H∞filtering for neutral systems with time-varying delays and nonlinear perturbations

DANGShengchao1,SUYakun2

(1. College of Mathematics and Physics, Bohai University, Jinzhou 121013, China; 2. The basic teaching department, Bohai University, Jinzhou 121013, China)

The problem ofH∞filtering for uncertain linear neutral systems with mixed time-varying delays and nonlinear perturbations is discussed in this paper. Based on the mixed time-varying and nonlinear pertuibations, a novel Lyapunov functional is constructed. A new delay-dependent stability criterion is derived to guarantee the robust stability of the neutral system. The Lyapunov Krasovskii stability theory and LMI technique and the convex combination technique are adopted to reduce the conservatism of obtained results. Some new delay-dependent sufficient conditions are presented to ensure that the filtering error system is asymptotically stable with a prescribed level ofH∞noise attenuation. In order to use MATLAB toolbox, the study changes the stability criterion into linear matrix inequality, and gets the corresponding date. The method to get the criterion is more conservative compared with the existing literature. Finally, one numerical example is given to illustrate the effectiveness of the proposed method.

neutral systems; uncertain;H∞filtering; delay-dependent; nonlinear perturbations; LMI(Linear matrix inequality)

2016-10-02。

国家自然科学基金青年科学基金资助项目(61403043)。

党胜超(1992-),女,辽宁朝阳人,渤海大学硕士研究生; 通信作者: 苏亚坤(1977-),女,辽宁朝阳人,渤海大学副教授,博士。

1673-5862(2017)01-0055-06

O19; TP13

A

10.3969/ j.issn.1673-5862.2017.01.010