做一个会“变脸”的小宠物

龚莹瑜 谢作如

川剧变脸是川剧的特技之一，演员在舞台上的一抬手一提足，脸上的面具都可能发生翻天覆地的变化，满满的神秘感、震撼的舞台效果，都给了观众不一样的体验。

偶然间看到DFRobot社区的一个表白神器——跳动的心（如图1），一个火柴盒大小的点阵屏，非常适合作为送给女友的小礼物、小伙伴的爱心玩具等。这个创意让我心动，也引发了我的思考：点阵屏能够画出爱心，那能不能绘制出脸谱呢？

● 器材和原理

创客空间刚好有盛思的Duinoplus box实验箱，这款教学套件整合了8×8的点阵屏（如图2），很适合做变脸的研究。所谓的8×8是指点阵屏由8行8列的LED组成，共有64个点组成，可以显示简单的图形。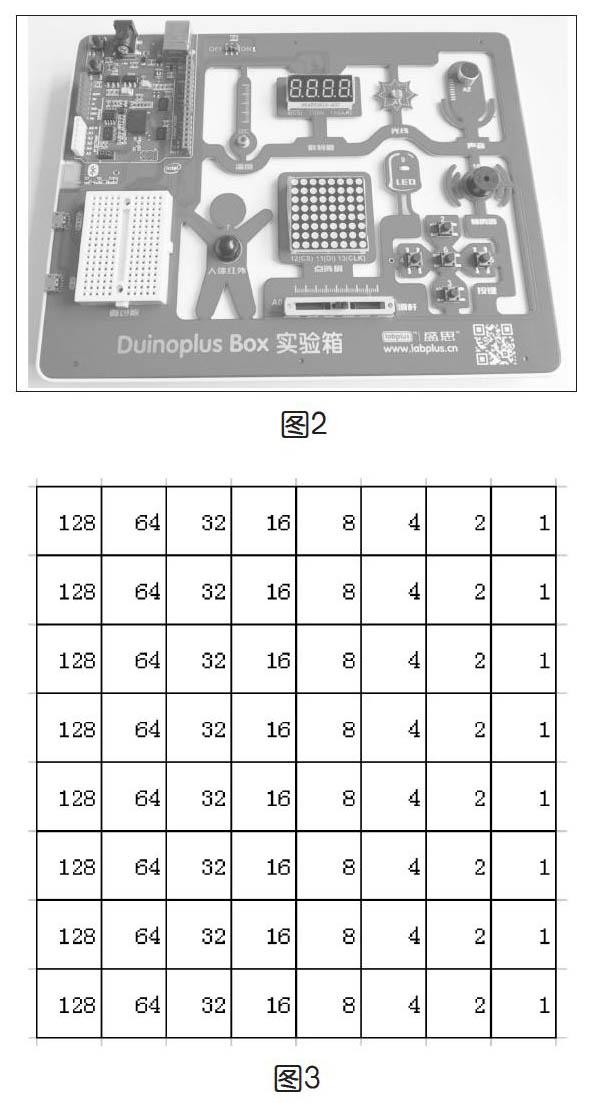

这款点阵屏不仅可以用X、Y来定位，精确控制某一个LED的状态，也可以用行、列赋值的方法，给某一行写一个参数，以点亮相应的LED。行赋值的代码以二进制为基础，每一行对应的是8位二进制，左边的位高，右边的位低（如图3），赋的值是该行所有亮的点对应值之和。如果给第一行赋值1（十进制），则最右边的LED亮，其他都暗；赋值255，则所有的LED亮。因为十进制的1对应的二进制数为“00000001”，255对应的则是“11111111”。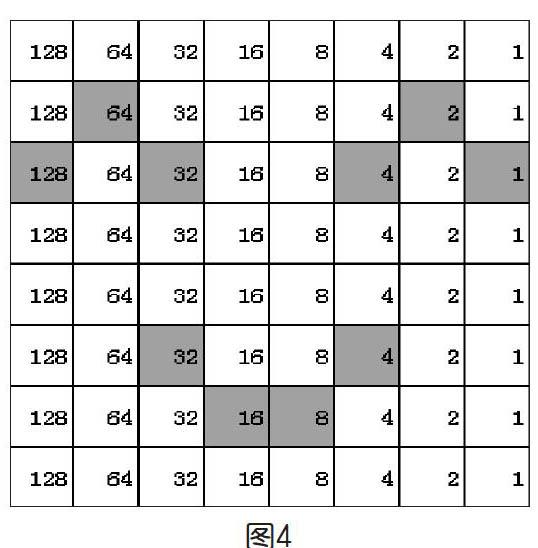

为了更好地理解行赋值，需要先学习二进制。二进制是逢2进位的进位制。0、1是基本算符。二进制数据也是采用位置计数法，其位权是以2为底的幂。最后一位是2的0次幂，倒数第二位是2的1次幂，以此类推。

所以把二进制化成十进制只需要将数值乘以2的幂次相加即可。例如，把二进制11111111转化为十进制，*1+*1+*1+*1+*1+*1+ *1+*1+*1=255。

知道了如何点亮点阵屏后，又一个问题来了——如何用点阵屏显示图片呢？其实位图都是由像素点组成的，只是平时我们看到的图片像素点很多，而且像素点又很小，所有我们看图片的时候很难发现。如果把图片一直放大，就能发现图片上出现了马赛克一样的方格，这就是像素点。所以点阵屏上的这64个点就相当于“像素点”，而我们要做的就是利用这些像素点绘制出不同的脸谱。

● 绘制脸谱

知道了点阵屏的点亮方法和绘图的原理之后，接下来我们就可以在点阵屏上开始绘制脸谱了。

打开Excel，模拟点阵屏的排布建立一个8×8的表格。然后，在表格中确定图案所对应的单元格位置，然后求出每行所对应的值。如图4中画出的是一张笑脸。

观察图4可知：

第0行：*0+*0+*0+*0+*0+*0+ *0+*0+*0=0。

第1行：*0+*1+*0+*0+*0+*0+ *0+*6+*0=66。

第2行：*1+*0+*0+*1+*0+*0+ *1+*0+*1=165。

第3行：*0+*0+*0+*0+*0+*0+ *0+*0+*0=0。

第4行：*0+*0+*0+*0+*0+*0+ *0+*0+*0=0。

第5行：*0+*0+*1+*0+*0+*1+ *0+*0+*0=36。

第6行：*0+*0+*0+*1+*1+*0+ *0+*0+*0=24。

第7行：*0+*0+*0+*0+*0+*0+ *0+*0+*0=0。

确定了每行所对应的值后，就可以开始点亮点阵屏了。每个脸谱都由8行点阵组成，为了让代码能简洁明了，我们用8个长度的数组来存储点陣屏中每行所对应的值。然后，利用循环语句对数组中的各个值进行读取，把这些值赋给对应的行，让点阵屏上显示笑脸。同理可以绘制其他的脸谱，如图5所示的三组数字，分别代表笑脸、哭脸和无表情的脸。

● 实现变脸

准备工作完成了，接下来我们开始编写代码，以便控制点阵屏实现“变脸”的过程。“变脸”的工作流程如下：当程序开始运行的时候，点阵屏上显示一种脸谱；当左、中、右按钮被按下的时候，分别出现不同的脸谱。相对来说，代码的编写倒最简单。当按钮按下时是高电位，也就是1电位，松开时是低电位，也就是0电位，可以用逻辑模块中的等于节点进行编程，也可以把按钮模块作为条件，因为没有说明时，就是默认条件是高电位。完整的代码如图6所示，效果图如图7所示。

● 拓展升级

利用实验箱制作的作品仅仅是原型，不够美观，也不好展示。我们的最终作品应该利用体积较小的Arduino板子和点阵屏模块，结合3D打印合，呈现各种有趣的作品形态，如会变脸的小宠物、钥匙挂坠等。图8所示的作品，是不是很酷炫？

如果对相关内容感兴趣，请关注主持人博客。