反应堆压力容器概率断裂力学计算中的不确定性分析

王东辉， 李 锴， 张 静

(国核电站运行服务技术有限公司， 上海 200233)

反应堆压力容器概率断裂力学计算中的不确定性分析

王东辉， 李 锴， 张 静

(国核电站运行服务技术有限公司， 上海 200233)

为评价输入参数对反应堆压力容器特定运行事件下失效概率计算结果的影响，建立了反应堆压力容器概率断裂力学计算模型，对计算所用主要参数进行敏感性分析，得到了缺陷类型及形状、辐照脆化程度、材料化学成分及温预应力对容器失效概率的影响，并分析了各参数的敏感程度.结果表明：输入参数的可靠性是保证概率断裂力学分析结果可靠有效的前提，材料化学成分及缺陷深度等参数对计算结果有重要影响.

反应堆压力容器； 概率断裂力学； 参数； 不确定性

反应堆压力容器(RPV)是反应堆冷却剂系统压力边界最重要的安全相关部件，作为反应堆冷却剂系统的一部分，其结构完整性直接影响电厂的安全和寿命.通常采用确定性或概率的方法对RPV进行结构完整性评价，采用上述2种方法预测其失效载荷及运行寿命时，均不可避免地存在不确定性.除了已知材料特性的分散性外，未预计的载荷以及材料老化机理也很难包含在计算模型中.此外，与制造、运行和维修等活动相关的人为因素也会影响结构的可靠性.国家法规从安全和经济性的角度出发，规定RPV的设计必须保证在结构完整性方面具有很高的可靠性，其失效概率应保持在一个极低的水平.

传统的工程分析方法是基于确定性的分析方法，采用确定的安全系数，并选用输入参数(如载荷、材料强度、制造缺陷以及材料降质和老化速率等)的边界值来考虑分析方法的不确定性.随机概率评价方法[1]采用概率分布函数来描述某些输入参数，以此来覆盖大部分输入参数的不确定性，其他的不确定性仍采用确定性方法中使用的保守的模型假设和保守值.由此可以看出，即使采用概率评价方法进行评价，其预测失效概率结果与实际情况相比也可能高出很多.

为了明确概率断裂力学(PFM)方法中各输入参数对分析结果的影响，笔者通过对缺陷分布、辐照脆化预测曲线和材料化学成分等特定参数的分析，为RPV结构完整性评价中参数选取提供支持，同时可为评价设计、材料选择、在役检查大纲的制定以及维护措施变更提供借鉴.

1 PFM分析模型

以压力容器环带区为研究对象，采用反应堆压力容器概率断裂力学计算软件FAVOR[2]进行分析，计算不同缺陷类型及尺寸、辐照脆化程度及材料化学成分等参数条件下RPV的条件失效概率，从而分析得到模型各主要参数对计算结果的影响.

1.1 结构参数

容器筒体区采用环形锻件焊接而成，堆芯环带区高度为4 200 mm，计算模型包含环带区及两端环向焊缝，计算高度取4 800 mm.其他结构参数如下：母材内径为3 975 mm，母材壁厚为210 mm，堆焊层厚度为5.5 mm.

1.2 材料参数

RPV母材、焊材和堆焊层的材料参数采用ASME第II卷(1998版)[3]中的相应数据，各参数均随温度变化，其中间温度对应的参数值通过3次艾米插值得到.表1给出材料在20 ℃和260 ℃下的性能参数，计算中不考虑材料弹塑性的影响.

1.3 计算瞬态

选用国际原子能机构(IAEA)组织的CRP9项目中使用的承压热冲击(PTS)瞬态输入[4]，该瞬态是经过大量的分析筛选之后获得的，相对较为保守.同时，该瞬态也是欧盟经合组织核能机构(OECDNEA)组织的RPV结构完整性分析研究(PROSIR)项目中的Tr3瞬态，具体如图1所示.

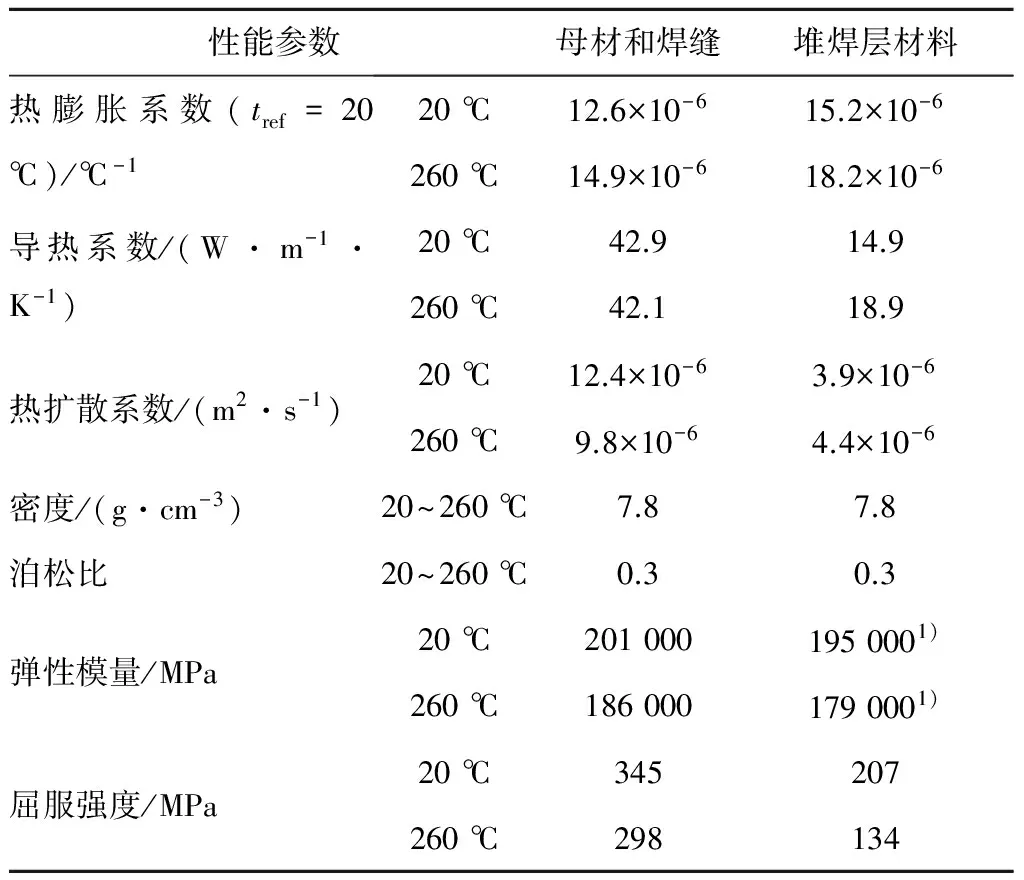
表1 材料性能参数1)

注：1) 采用ASME 2010中相应数据.

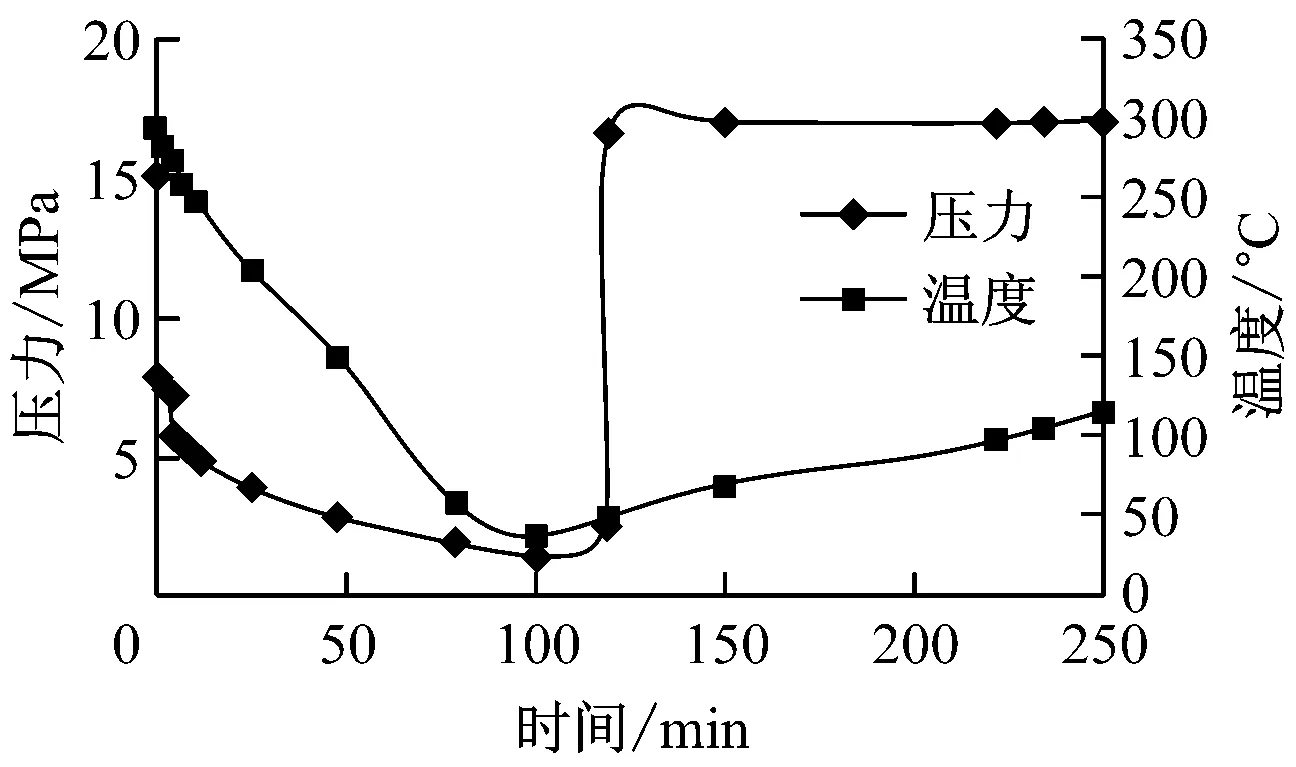
(a) 压力、温度随时间的变化

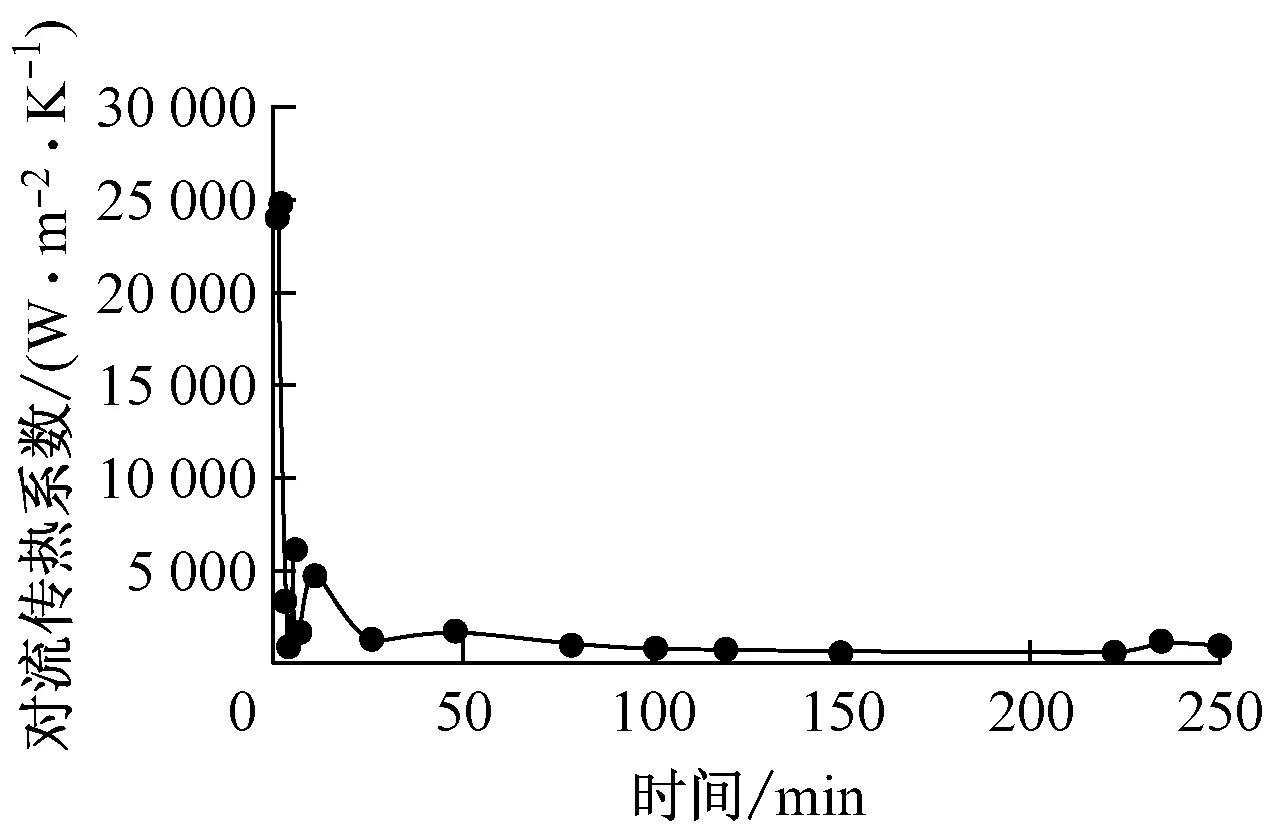
(b) 对流传热系数随时间的变化

2 计算方法

采用概率断裂力学方法，在分析瞬态的每个离散时间步上进行确定性断裂力学分析，通过比较作用于假想裂纹尖端的应力强度因子KI与断裂韧性KIC之间的瞬态关系，可以得到在时间步τ处，对应第i个瞬态、第j个RPV序列和第k个缺陷的瞬时条件起裂概率p(τn)(i,j,k).

(1)

式中：τn为瞬态i的第n个时间步；KI(τn)(i,j,k)为对应第i个瞬态、第j个RPV序列和第k个缺陷的应力强度因子；aKIC、bKIC、cKIC为断裂韧性KIC的分布参数.

综合考虑各离散时间步，即可得到条件起裂概率如下：

(2)

参数敏感性分析方法主要通过改变单一输入参数，并保持其他输入变量不变，然后计算出输出变量的变化.如果输入变量的改变引起输出变量发生很大变化，那么输出变量对该输入变量的敏感性高[5].采用上述方法对计算所用的缺陷类型、形状和深度，材料辐照脆化，材料化学成分等因素进行分析，可定量评价反应堆压力容器PTS事件分析中与失效概率相关的输入参数的有效性.

3 结果与分析

分析得到对应假想瞬态不同时间条件下容器沿壁厚方向的温度分布和环向应力分布，以及假想1/4壁厚轴向缺陷尖端应力强度因子随时间的分布，如图2所示.

(a) 不同时间下沿容器壁厚方向温度分布

(b) 不同时间下沿容器壁厚方向环向应力分布

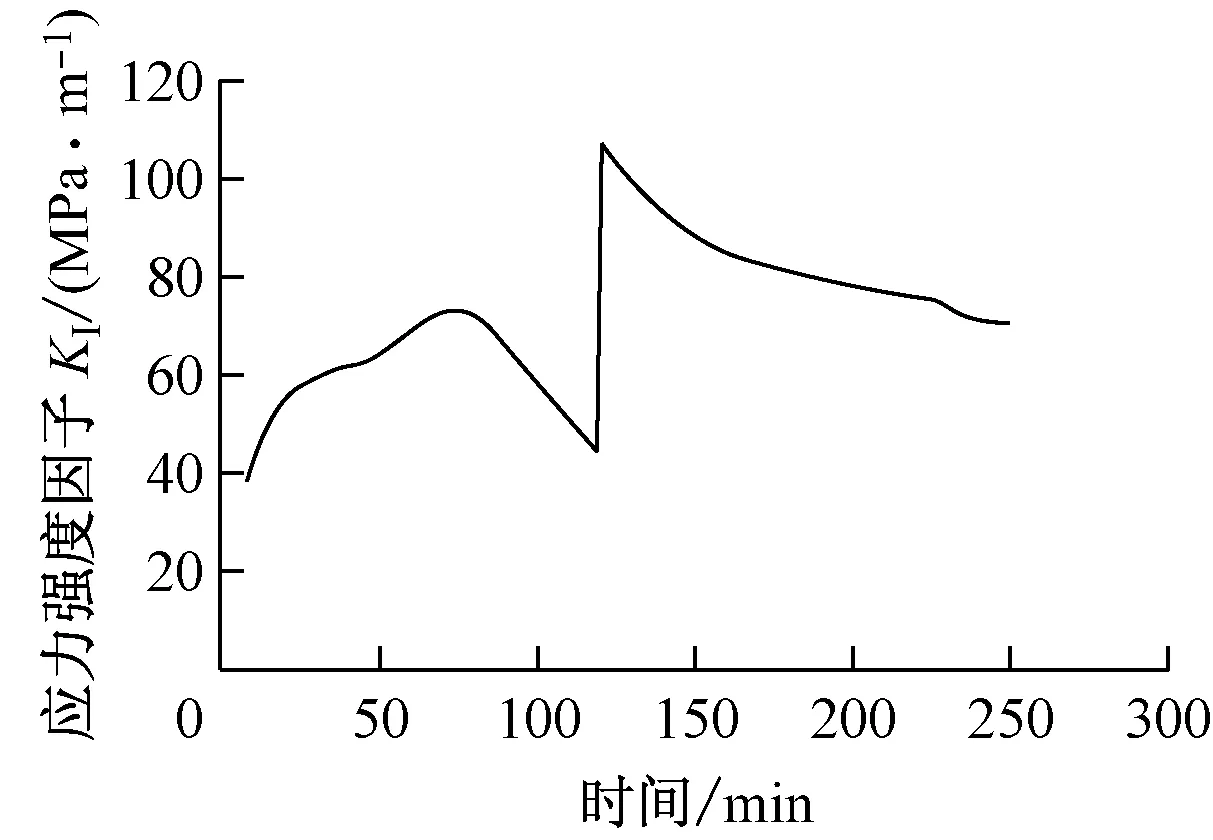
(c) 假想缺陷尖端应力强度因子随时间的分布

3.1 缺陷类型对结果的影响

选择2种不同的缺陷深度概率分布模型，分别如图3(a)和图3(b)所示.其中，图3(a)为Marshall报告[6]中给出的基于对有限数量的核压力容器以及多个非核容器缺陷检测结果得出的指数分布规律.受到早期无损检测能力的限制，该分布只适用于缺陷深度较大的情况.在浅层缺陷范围内，取其分布趋势与图3(b)中焊缝缺陷分布一致.图3(b)为美国核管会(NRC)发起的反应堆压力容器PTS重新评估项目中所用的缺陷统计分布[7].分析结果如图4所示.由图4可以看出，在其他参数不变的条件下，表面缺陷及浅层缺陷对容器失效概率的影响较大.

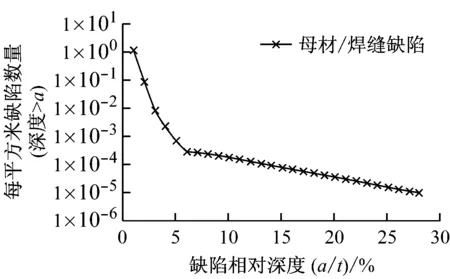
(a) Marshall分布

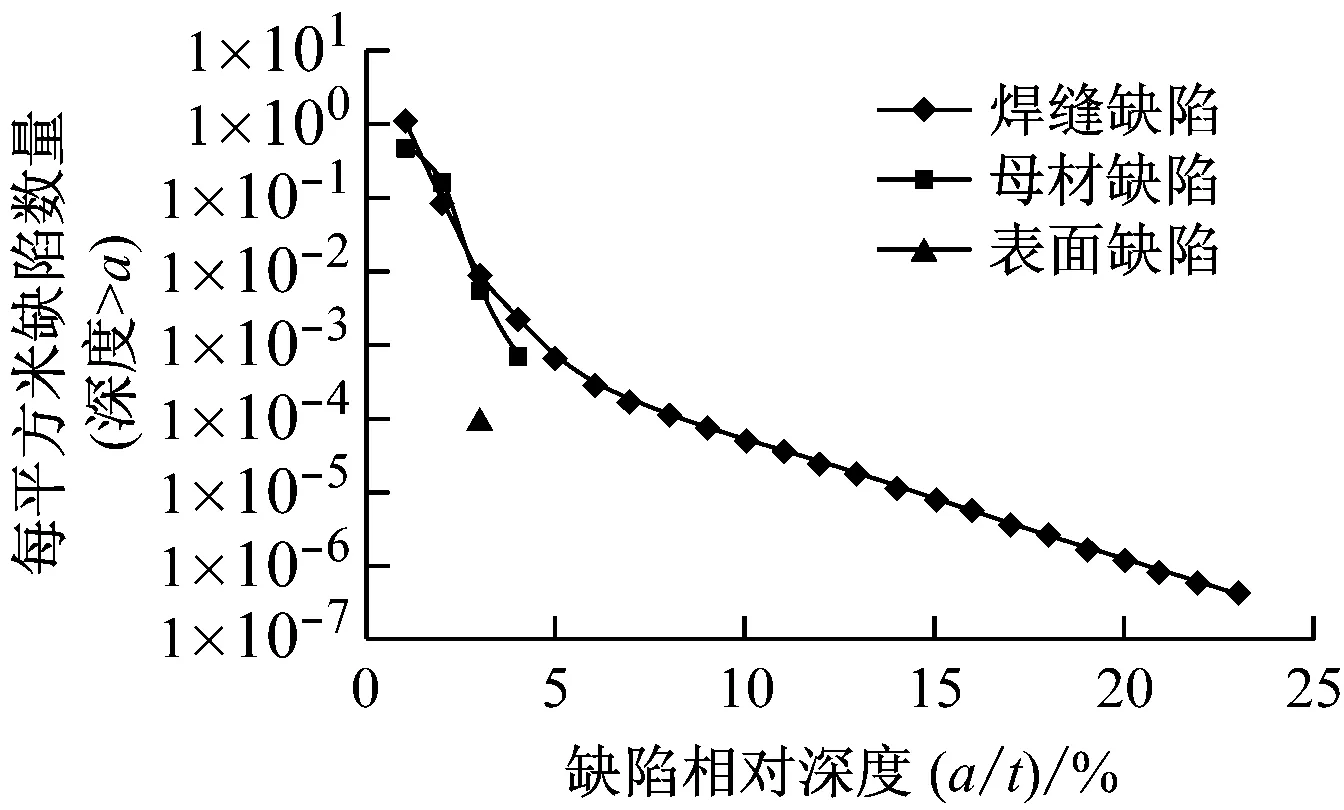
(b) VFLAW采用的分布

3.2 缺陷形状对结果的影响

为考虑缺陷形状对容器失效概率的影响，假设长深比(2c/a)分别为2、6、10及无限长，计算缺陷形状对客器失效概率的影响，结果如图5所示.由图5可以看出，缺陷长深比对容器失效概率的影响较小.

3.3 材料辐照脆化对结果的影响

采用RG1.99第2版[8]、Eason 2000[9]及Eason 2006[10]3种无延性韧脆转变温度(RTNDT)受辐照影响预测模型，分别计算辐照脆化预测模型对容器失效概率的影响，结果如图6所示.

图4 缺陷深度对容器失效概率的影响

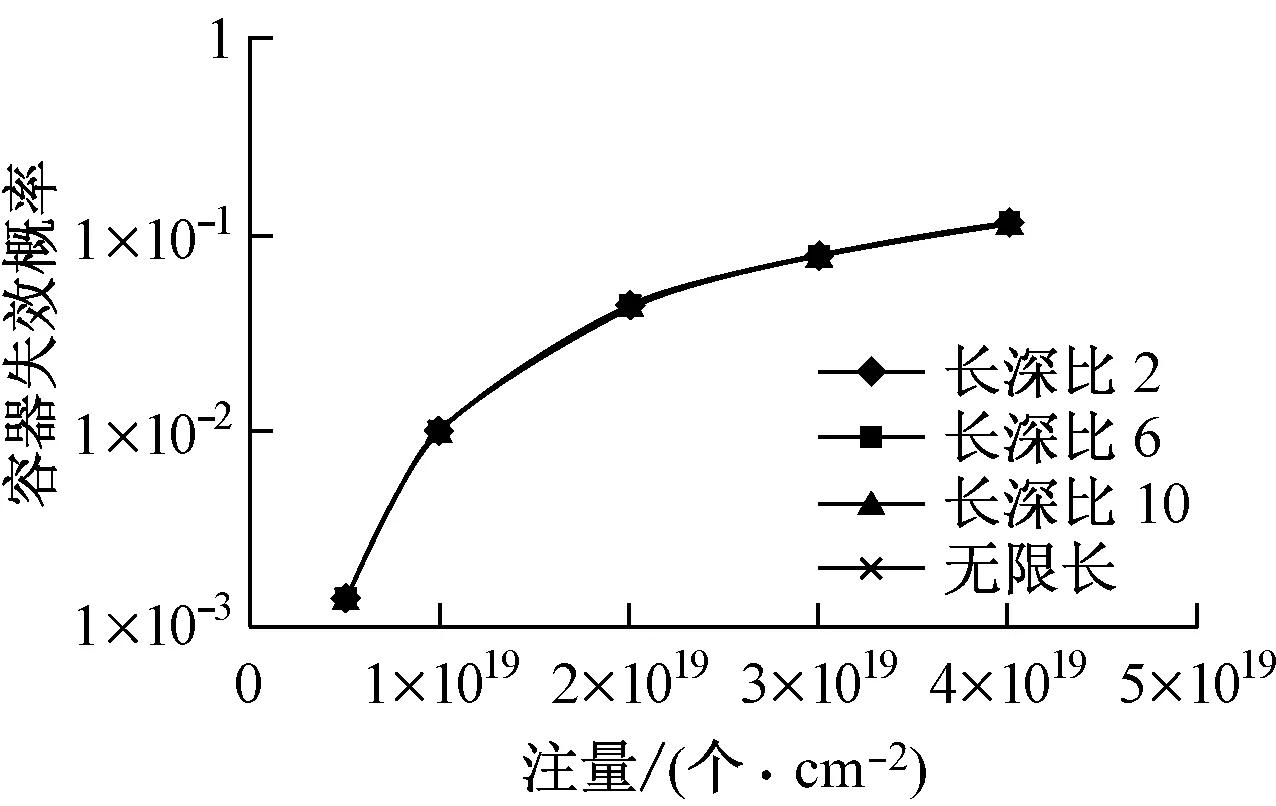
图5 缺陷形状对容器失效概率的影响

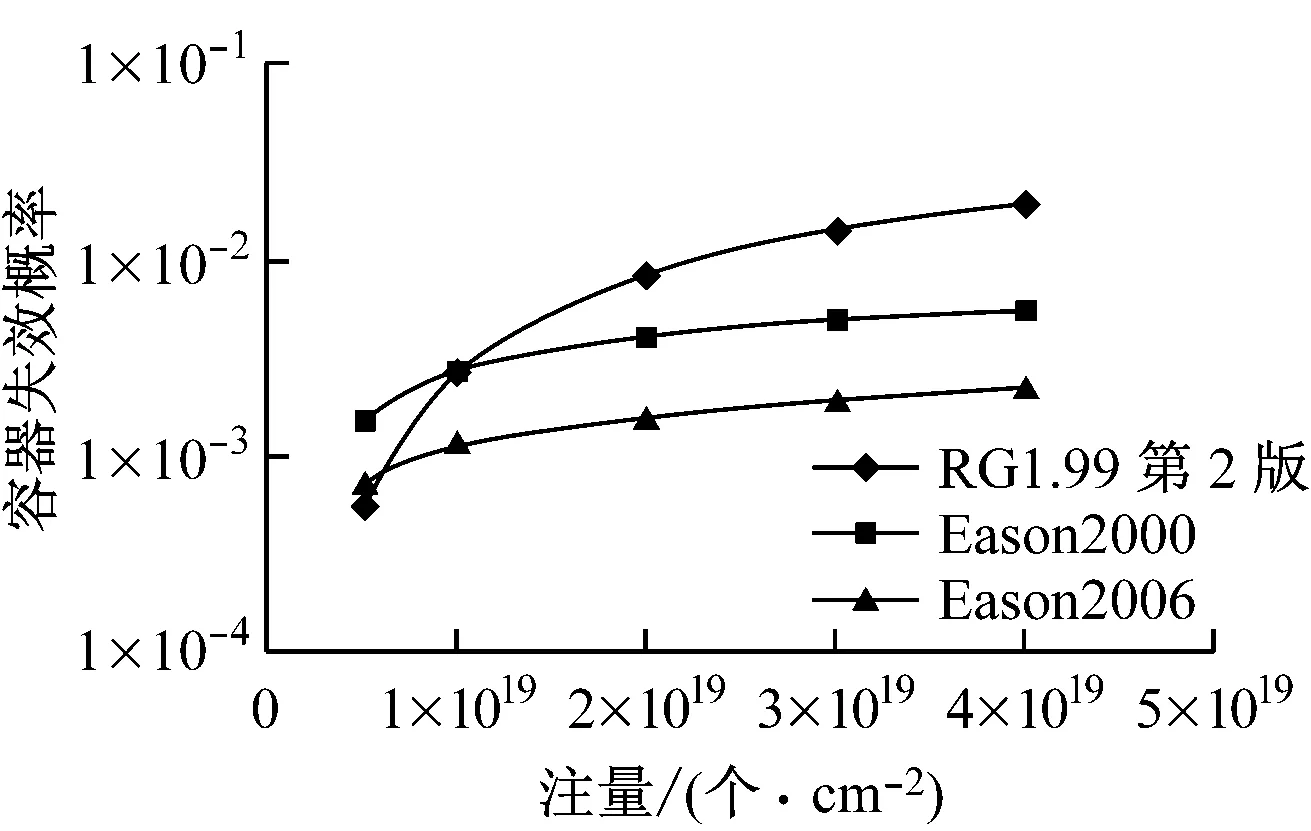
图6 辐照脆化预测模型对容器失效概率的影响

从图6可以看出，采用不同辐照脆化预测模型计算得出的容器失效概率明显不同.在注量较低的情况下，Eason 2000保守程度最高，在高注量情况下，RG1.99第2版计算结果最为保守.

3.4 材料化学成分对结果的影响

对于反应堆压力容器来说，材料中Cu和Ni的质量分数对评价容器辐照脆化有重要影响.从计算材料RTNDT偏移公式可以看出，Cu质量分数的影响较Ni元素等其他元素质量分数的影响更大.为此，通过分析得到Cu质量分数对容器失效概率的影响，如图7所示.

从图7可以看出，随着Cu质量分数的增加，容器失效概率随之增大，并且在低质量分数情况下更为明显.

3.5 温预应力

温预应力对铁素体钢影响的研究最早开始于约40年前，并逐步得到深入研究.近年来，温预应力对反应堆压力容器完整性评价的影响已经得到各种试验验证.笔者通过计算评价了温预应力对容器失效概率的影响.假设在应力强度因子KI下降的过程中，裂纹不会起裂扩展.温预应力对容器失效概率的影响如图8所示，在考虑温预应力的情况下，容器失效概率有一定降低.

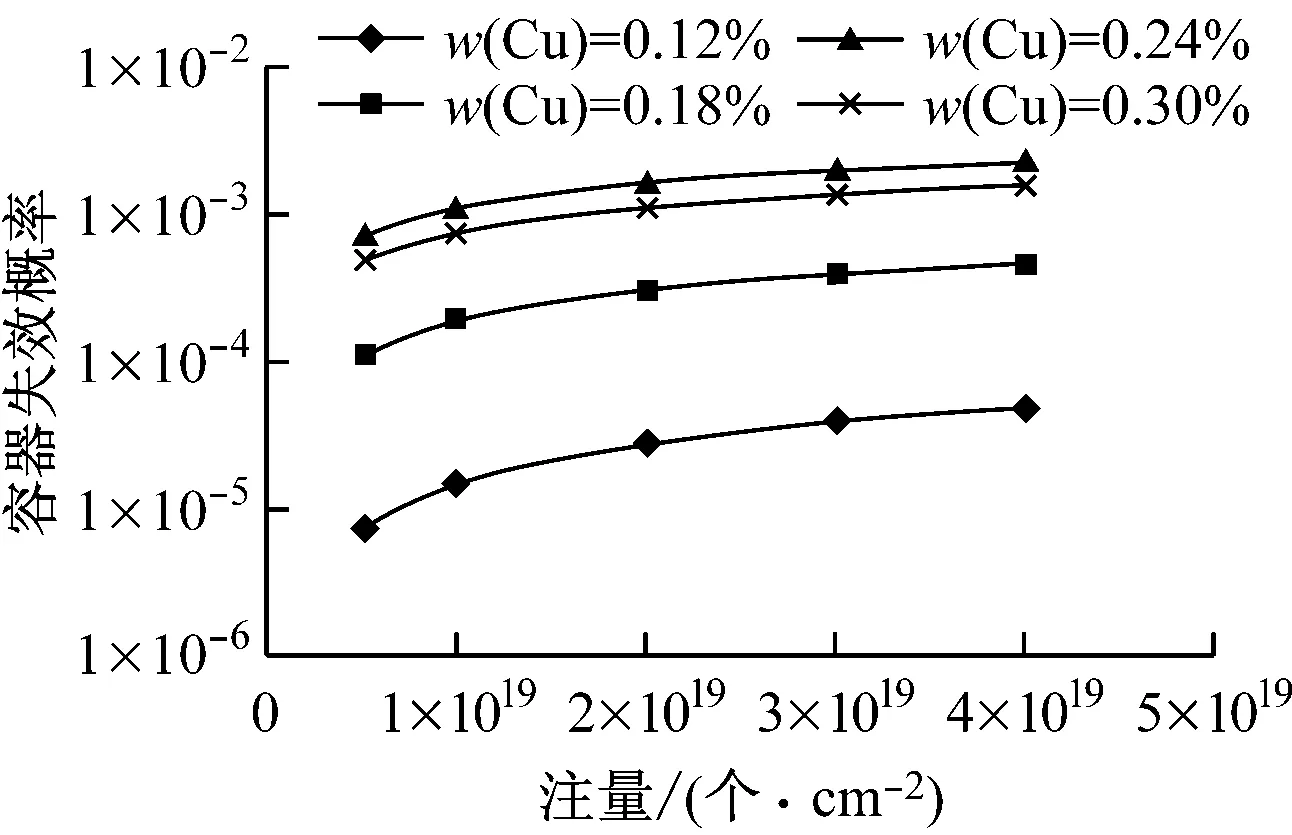
图7 材料Cu质量分数对容器失效概率的影响

图8 温预应力对容器失效概率的影响

4 结 论

(1) 缺陷深度、RTNDT辐照脆化模型和材料化学成分等参数对容器失效概率有较大影响.

(2) 缺陷长深比对容器失效概率影响较小.

(3) 在考虑温预应力的条件下，容器失效概率会有一定程度降低，尤其在注量较低的情况下，温预应力对容器失效概率的影响更为明显.

[1] 韩志杰, 王璋奇. 基于区间有限元的汽轮机叶片非概率可靠性分析[J]. 动力工程学报, 2012, 32(4): 296-301, 337.

HAN Zhijie, WANG Zhangqi. Non-probabilistic reliability blade based on interval analysis of steam turbine finite element method[J]. Journal of Chinese Society of Power Engineering, 2012, 32(4): 296-301, 337.

[2] Oak Ridge National Laboratory. Fracture analysis of vessels-oak ridge FAVOR, v04.1, computer code: theory and implementation of algorithms, methods, and correlations, NUREG/CR-6854[R]. Washington, USA: U.S. Nuclear Regulatory Commission, 2007.

[3] The American Society of Mechanical Engineers. Boiler and pressure vessel code, section II, materials[S]. New York, USA：ASME, 1998.

[4] International Atomic Energy Agency. Pressurized thermal shock in nuclear power plants: good practices for assessment, IAEA-TECDOC-1627[R]. Vienna,Austria: IAEA, 2010.

[5] 段巍, 王璋奇. 基于响应面方法的汽轮机叶片概率强度设计及敏感性分析[J]. 中国电机工程学报, 2007, 27(5): 99-104.

DUAN Wei, WANG Zhangqi. Probability strength design of steam turbine blade and sensitivity analysis with respect to random parameters based on response surface method[J]. Proceedings of the CSEE, 2007, 27(5): 99-104.

[6] United Kingdom Atomic Energy Authority. An assessment of the integrity of PWR pressure vessels: second report by a study group under the chairmanship of Dr W Marshall Cbe Frs[M]. Warrington, UK: UK Atomic Energy Authority, 1982.

[7] SIMONEN F A. A generalized procedure for generating flaw-related inputs for the favor code, NUREG/CR-6817[R]. Washington, DC: U.S. Nuclear Regulatory Commission, 2003.

[8] U.S. Nuclear Regulatory Commission. Radiation embrittlement of reactor vessel materials, regulatory guide 1.99 rev. 2[S]. Washington, USA: U.S. Nuclear Regulatory Commission, 1988.

[9] KIRK M T, SANTOS C, EASON E, et al. Updated embrittlement trend curve for reactor pressure vessel steels. Paper No.G01-5[C]//Transactions of the 17th International Conference on Structural Mechanics in Reactor Technology (SMiRT 17). Prague, Czech Republic: International Association for SMiRT, 2003.

[10] Oak Ridge National Laboratory. A physically based correlation of irradiation-induced transition temperature shifts for RPV steels, ORNL/TM-2006/530[R]. Washington, USA: U.S. Nuclear Regulatory Commission, 2006.

Uncertainty Analysis on Calculation of Probabilistic Fracture Mechanics for Reactor Pressure Vessels

WANGDonghui,LIKai,ZHANGJing

(State Nuclear Power Plant Service Company, Shanghai 200233, China)

To evaluate the effects of input parameters on the calculation results of reactor vessel failure probability under specific operation conditions, a calculation model for probabilistic fracture mechanics of reactor pressure vessel(RPV) was established for sensitivity analysis on main parameters applied in the calculation, so as to study the influence of various factors on the RPV failure probability, such as the defect type and shape, irradiation embrittlement degree, material chemical composition and warm pre-stressing, etc., and to analyze the sensitivity of each parameter. Results show that reliable input parameters are the prerequisite to ensure the reliability and validity of analysis results for probabilistic fracture mechanics. In addition, the material chemical composition and defect depth are key factors influencing the calculation results.

reactor pressure vessel; probabilistic fracture mechanics; parameter; uncertainty

2016-02-02

2016-04-06

国家科技重大专项资助项目(2015ZX06002005)

王东辉(1980-)，女，辽宁沈阳人，硕士研究生，主要从事反应堆压力容器及管道完整性评价方面的研究. 电话(Tel.)：18930176792；E-mail：wangdh@snpsc.com.

1674-7607(2017)02-0163-04

TL351+.6

A 学科分类号：490.40