双孔射流流化床内颗粒混合特性的离散单元法数值模拟

张俊强， 纪 律， 李 斌， 陈海生， 边禹铭

(1.华北电力大学 能源动力与机械工程学院， 河北保定 071003；2.中国科学院工程热物理研究所， 北京 100190)

双孔射流流化床内颗粒混合特性的离散单元法数值模拟

张俊强1,2， 纪 律2， 李 斌1， 陈海生2， 边禹铭1

(1.华北电力大学 能源动力与机械工程学院， 河北保定 071003；2.中国科学院工程热物理研究所， 北京 100190)

将计算流体力学与离散单元法相结合，采用Fortran语言编程，根据牛顿第三定律实现气固耦合，从微观角度剖析了颗粒在流化床内的运动机制.利用Lacey混合指数对流化床内不同特性区域的颗粒混合程度进行了定量分析，并研究了颗粒混合特性的影响因素，得到颗粒轴向和径向混合序列图、气体和颗粒速度分布以及整床和三区的颗粒混合指数分布.结果表明：颗粒受到空气射流作用后，随着混合和偏析的不断进行，最后达到随机完全混合状态；相同表观气速下颗粒轴向混合进程快于径向混合进程；表观气速增大，喷泉区尺度增大，使颗粒径向混合能力得到改善，但对轴向混合能力的影响微弱.

流化床； 轴向混合； 径向混合； 离散单元法； 混合指数

流化床凭借其特殊的气固流动特性和优良的结构形式，已在各个工业领域得到了广泛的应用.流化床内发生强烈的气固流动及相间反应，因此可作为高温蓄热设备，具有换热效果好和温度分布均匀等优点.

随着我国电力行业供给侧过剩和可再生能源的迅猛发展，发展电力储能系统已成为大规模利用可再生能源的有效措施，有助于提高我国常规电力系统的效率、安全性和经济性[1].流化床以其强大的传热和蓄热能力在储能领域的探索性应用上受到越来越广泛的关注.但由于流化床内两相间作用复杂，人们对流化床的微观反应过程尚未充分了解.流化床内气固两相运动对反应器中传热传质过程具有关键作用，而颗粒混合运动规律对其流动和传热过程也有重要影响.

一些学者[2-3]通过实验手段对流化床内气固流动特性进行分析，但因操作条件及设备实现难度较大，目前较难获得微观层面上的颗粒运动信息.近年来，随着数值模拟发展不断加快，诸多学者[4-5]通过数值模拟与实验研究相结合的方法来深入分析流化床内气固流动特性.其中离散单元法(DEM)具有获取微观信息丰富、模拟精确度高等优势，在气固两相流的模拟研究中得到了越来越多的应用[6-9].

目前，对流化床内颗粒混合机理进行剖析是流化床的研究热点之一[10-11].Sharma等[12]对鼓泡流化床内生物质与生物碳颗粒的混合与分离行为进行了数值模拟.Olaofe等[13]采用计算流体力学与离散单元法相结合的方法(CFD-DEM)研究了流化床内气固流动特性,并分析了颗粒的混合和偏析过程.朱润孺等[14]采用离散单元法研究了鼓泡床内颗粒的轴向和径向混合特性.但对数值模拟与实验结果对比，且从微观层次进行的较为全面的定量研究还较少.

笔者将计算流体力学与离散单元法分别应用于气相与固相的数值计算，采用Fortran语言自行开发数值模拟程序，对流化床内颗粒的轴向、径向混合过程进行模拟，并利用实验结果对其进行验证，分析了气体和颗粒在流化床内的流动特性，研究了颗粒的轴向、径向混合特性及其影响因素.同时采用Lacey混合指数对双孔射流流化床内颗粒的混合程度进行定量分析，揭示了颗粒由完全分离状态到随机完全混合状态的过程机理.

1 数学模型

1.1 气固两相运动模型

流化床内颗粒主要受气体的曳力、自身重力以及颗粒与颗粒(壁面)之间碰撞力的作用[10].气相模型采用Navier-Stocks方程，湍流运动采用k-ε两方程数学模型[10].

1.2 气固两相之间的耦合作用

1.2.1 气相对颗粒的曳力

采用文献[9]中的曳力模型，气相对颗粒的曳力如下：

当εg>0.8时，利用Wen&Yu等方程可得

(1)

当εg≤0.8时，采用Ergun等式可得

(2)

(3)

式中：n为空隙率修正因子，一般n的取值为4.65；Cd为单颗粒的曳力系数.

当颗粒雷诺数Rep≤1 000时，

(4)

当Rep>1 000时，

(5)

其中，颗粒雷诺数为

(6)

空隙率为

(7)

式中：ΔV为划分区域的网格体积；kc为所划分网格内颗粒的个数.

1.2.2 固相对气相的反作用力

(8)

式中：Fp为固相对气相的反作用力.

2 模拟对象及参数

2.1 模拟对象

模拟的床体为长×宽×高=150 mm×4 mm×900 mm的双喷口矩形截面准三维流化床，床身底部32.5～42.5 mm、107.5～127.5 mm位置分别设置一个空气进口，空气进口宽度为10 mm，如图1所示.

图1 模拟床体示意图

床体顶部出口位置采用局部单向化处理.气相和固相在近壁面处分别设置为无滑移边界条件和滑移边界条件.模拟中固相采用2 400个直径均为4 mm的球形颗粒.

2.2 模拟参数

对不同表观气速下双孔射流流化床内2种组分固相的动态混合过程进行模拟，并分析其影响因素，其中气相和颗粒的基本参数见表1.

3 模拟结果

3.1 流化床内颗粒的流化过程图

首先将起始床层的颗粒根据轴向混合、径向混合均分成2组，以确保颗粒最初为完全分离状态.图2和图3为表观气速v=2.0 m/s、计算时间t=0～1.8 s时颗粒的混合序列图.结合图2和图3可知，t=0 s时2种颗粒处于彼此分离状态，随着喷动气流向上流动，颗粒混合不断深入.喷动气流从环隙区渗入喷射区，并将其底部颗粒夹带到喷泉区，颗粒上行穿过床层表面后分别向两侧扩散.在扩散过程中当颗粒自身重力大于曳力时，颗粒开始下行，并与其他颗粒不断碰撞混合，缓慢下移至环隙区底部后，又被卷吸至喷射区，重新进入下一循环.颗粒在此循环过程中与周围颗粒不断进行混合与扩散，混合程度不断加深，最后达到颗粒混合的动态平衡.由此得出，由气体携带作用引起的颗粒循环对其混合效果有关键影响.对比图2与图3可知，2种组分颗粒在未达到完全混合前，相同时刻下颗粒轴向混合比径向混合更充分.以上模拟结果与文献[10]和文献[11]中结果一致.

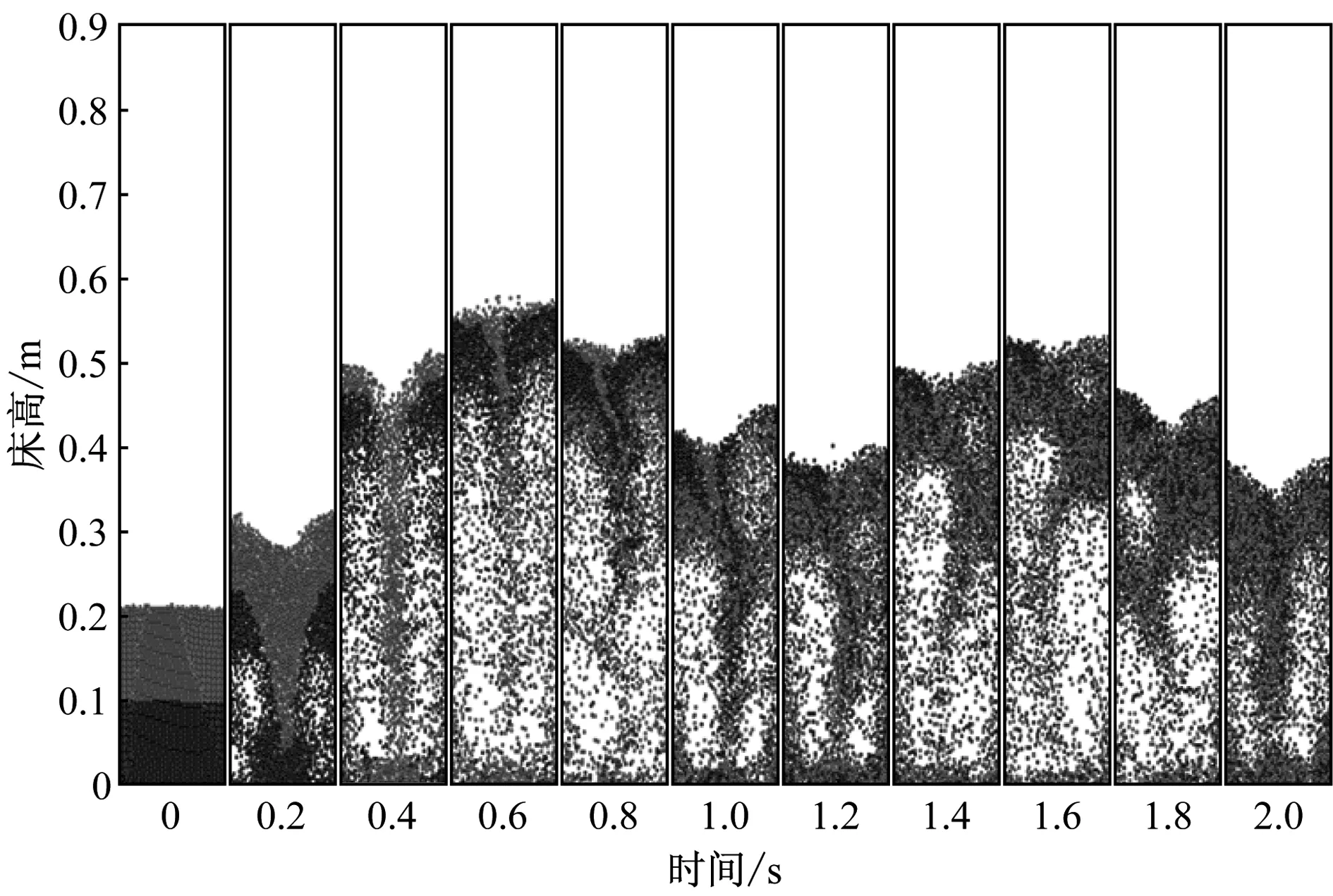
图2 颗粒轴向混合序列图

图3 颗粒径向混合序列图

为了验证以上模型及模拟的准确性，进行了相关实验研究，测量了相同条件下流化床内颗粒流场瞬时图.图4给出了颗粒流动模拟与实验中瞬时图的对比.由图4可以看出，模拟与实验中床层颗粒轴向、径向混合时，颗粒由完全分离状态到混合状态均具有较好的一致性.

图4 颗粒流动模拟与实验中瞬时图的对比

3.2 气体速度分布

图5(a)和图5(b)分别给出了流化床内不同床高h处的气体水平速度和垂直速度分布.由图5(a)可以看出，在床层底部，每个喷口左右两侧的气体水平速度符号均相反，这是因为进口射流的卷吸作用使气体从两侧向喷口中心聚集.在左侧喷口较高床高位置处，气体水平速度平均值为正值；在右侧喷口较高床高位置处，气体水平速度平均值为负值，这主要是由于双喷口位置相对于床体中心更靠近壁面，使得从喷口喷出的气体在较高床高位置处向壁面方向的运动受限，且在与壁面作用后反向运动.由图5(b)可以看出，相同床高、靠近2个喷口竖直方向轴线处的气体速度大于两侧区域的气体速度，且由于2个喷口处的气体水平速度存在相互扰动，所以在较高床高位置处，气体垂直速度最大值向两侧偏移.两侧气体速度绝对值随着床高的增加而减小，而中间气体速度绝对值随着床高的增加呈增大趋势.对比图5(a)与图5(b)可知，相同床高处气体垂直速度明显大于水平速度，气相对颗粒的曳力作用是颗粒运动的主要影响因素，进而使颗粒的轴向混合比径向混合更剧烈.

3.3 颗粒速度分布

图6给出了0～1.8 s内不同床高处的颗粒时均速度分布.由图6(a)可以看出，由于2个喷口之间存在相互扰动，在床层底部，左侧喷口处的颗粒水平速度为负值，此时颗粒往左侧移动，右侧喷口处的颗粒水平速度为正值，此时颗粒往右侧移动；而在较高床高位置处，流动规律呈相反趋势.由图6(b)可以看出，2个喷口处的颗粒垂直速度为正值，此时颗粒向床层表面移动.由于2个喷口之间存在较强的横向扰动，随着床高的增加，2股主喷射气流向两侧壁面偏移，在靠近壁面处有连续的气体作用于颗粒，此时颗粒在主喷射气流的携带作用下向上运动，颗粒上行至床层表面后向中心汇集.中心处的颗粒垂直速度为负值，这是因为中心处气体速度较小，颗粒自身重力大于曳力，因此颗粒向下运动，运动到床体下部后往2个喷口处汇集并进入各自喷射区，从而构成一个完整的颗粒内循环.对比图6(a)与图6(b)可知，相同床高处颗粒垂直速度明显大于水平速度，从而导致颗粒的轴向混合明显强于径向混合.

(a)气体水平速度

(b)气体垂直速度

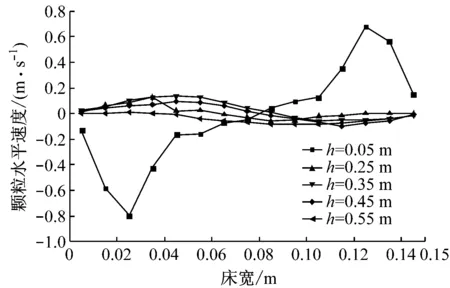
(a)颗粒水平速度

(b)颗粒垂直速度

图7为颗粒速度矢量图.由图7能够更直观地得出气相与固相作用后颗粒在流化床内的运动情况，由该图得到的颗粒移动进程与由颗粒混合序列图和颗粒速度分布图得出的颗粒运动相符，同时也证实了前文中气固流动特性分析的正确性.

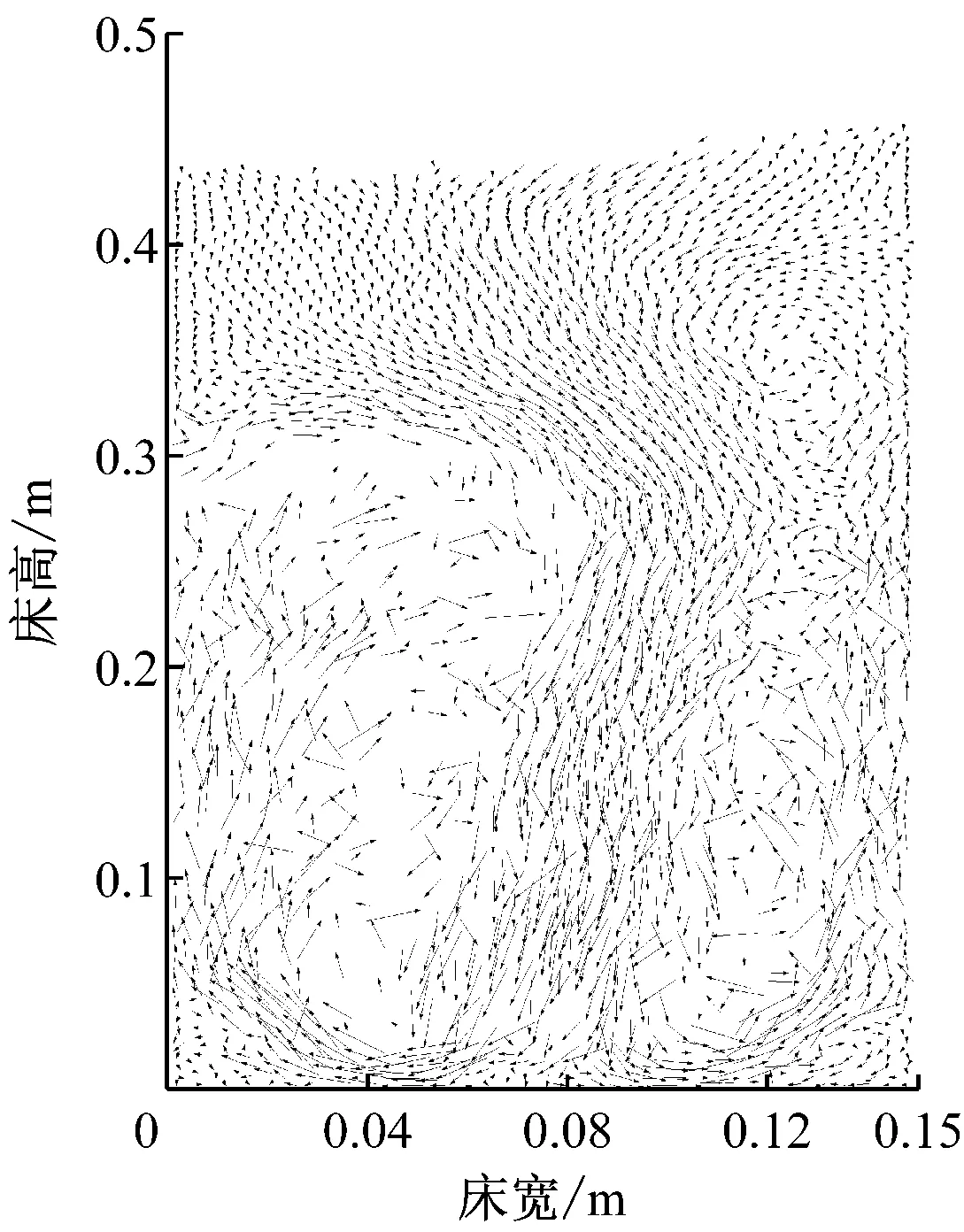
图7 颗粒速度矢量图

3.4 混合程度评价

随着颗粒混合运动不断进行，单从直观上对其混合程度进行分析难以得出可靠的结论.引入Lacey提出的混合指数M[4]，对颗粒的混合程度进行深入研究.选定图2和图3中的黑色颗粒为示踪颗粒，同时将床体平均分成若干个取样单元，对于有限取样过程，示踪颗粒质量浓度标准偏差为

(9)

(10)

混合指数M为

(11)

M为无量纲量，M=0表示2种组分颗粒处于完全分离状态，M=1表示2种组分颗粒处于随机完全混合状态，0

为了更全面地认识流化床内颗粒混合特性及其影响因素，将流化床分成5×30个取样单元，数据结果输出步长为0.01 s.图8给出了表观气速为2.0 m/s时颗粒轴向、径向混合指数的变化.由图8可以看出，在运动初始阶段，混合指数增速较快时颗粒彼此混合迅速；快速混合进行一定时间后，混合指数增速变缓，并在接近1处波动，此时可认为颗粒混合趋于随机完全混合状态，而波动表明混合过程经历着混合与偏析，由此达到动态平衡.由图8还可以看出，颗粒轴向、径向混合指数变化趋势区别较大，轴向混合指数起始增速快，在4 s左右达到随机完全混合状态；径向混合指数起始增速慢，在7 s左右达到随机完全混合状态.相同时刻下轴向混合进程快于径向混合进程[11]，这与图2、图3中颗粒的混合进程相符.

图8 颗粒轴向、径向混合指数M随时间的变化

通过计算网格来划分三区，即喷射区、喷泉区和环隙区，每个区域由9个计算网格进行统计计算.图9给出了该模拟条件下床体轴向、径向三区混合指数的变化.结合图8与图9可知，整床达到随机完全混合状态所需时间与环隙区混合指数达到平衡所需时间接近.对比图9(a)与图9(b)可知，随着混合时间的推移，颗粒轴向、径向混合不同区域的混合指数的变化趋势相似，但在环隙区存在较大差异.轴向混合时环隙区混合指数达到平衡所需时间较径向混合时短，这就是整床颗粒轴向混合进程快于径向混合进程的原因.综上可知，环隙区内颗粒的混合速度是决定流化床内颗粒达到随机完全混合状态的关键因素，这与文献[14]中研究结果相同.对比图9(a)与图9(b)还可知，喷泉区混合指数与其他2个区域的混合指数接近，表明喷泉区内颗粒混合较为充分，这一结果有别于单喷口流化床[14-15].由于双孔射流的存在增强了气相对颗粒的携带能力，混合颗粒到达床层顶部后的扩散能力增强，因而喷泉区内颗粒的混合更充分.

(a)轴向混合

(b)径向混合

图10给出了表观气速分别为2.0 m/s和2.33 m/s时颗粒混合指数的变化.对比图10(a)与图10(b)可知，增大表观气速对颗粒轴向混合进程的影响较小，但却有效地加快了颗粒径向混合进程.表观气速增大使颗粒轴向混合速度随之增大，而颗粒运动形成的床层尺度也相应增大，完成整个颗粒内循环的时间变化较小，导致轴向混合状态变化较小.而表观气速的增大可以有效增大喷泉区尺度，颗粒穿透床层后向两侧的运动速度加快，使颗粒径向扩散能力增强，即径向混合能力得到改善.

4 结 论

(1)流化床内相同床高处气体垂直速度明显大于水平速度，气相对颗粒的曳力作用是颗粒流动的主要影响因素，颗粒的轴向混合比径向混合更剧烈.

(2)喷动气流将从环隙区渗入喷射区内的颗粒夹带到喷泉区，颗粒上行到达床层顶部后分别向两侧进行扩散，扩散区域的气体速度减小，当颗粒所受曳力小于自身重力时，颗粒向上运动速度不断减小，之后颗粒开始向下运动，颗粒下行期间与周围颗粒不断碰撞混合，缓慢下移至环隙区底部后，又被卷吸至喷射区，再次进入下一循环，如此往复，混合程度不断加强，最后达到颗粒混合动态平衡.

(a)轴向混合

(b)径向混合

(3)相同表观气速下，颗粒轴向混合时达到随机完全混合状态所需时间较径向混合时短.

(4)表观气速增大，流化床内喷泉区尺度增大，使颗粒径向混合能力得到改善，但对轴向混合能力的影响微弱.

[1] CHEN H H, CONG T N, YANG W, et al. Progress in electrical energy storage system: a critical review[J]. Progress in Natural Science, 2009, 19(3): 291-312.

[2] SAIDI M, TABRIZI H B, GRACE J R, et al. Hydrodynamic investigation of gas-solid flow in rectangular spout-fluid bed using CFD-DEM modeling[J]. Powder Technology, 2015, 284: 355-364.

[3] 邵应娟, 金保昇, 钟文琪, 等. 流化床异重非球颗粒混合特性试验研究[J]. 工程热物理学报, 2013, 34(4): 672-675.

SHAO Yingjuan, JIN Baosheng, ZHONG Wenqi, et al. Experimental investigation of irregular particles mixing behavior in fludized bed[J]. Journal of Engineering Thermolphysics, 2013, 34(4): 672-675.

[4] LACEY P M C. Developments in the theory of particle mixing[J]. Journal of Chemical Technology and Biotechnology, 1954, 4(5): 257-268.

[5] 胡颢, 沙春发, 邵应娟, 等. 床料对固废流化床颗粒混合特性的影响[J]. 东南大学学报(自然科学版), 2013, 43(3): 525-530.

HU Hao, SHA Chunfa, SHAO Yingjuan, et al. Effect of bed material on particle mixing in solid waste fluidized bed[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(3): 525-530.

[6] 任立波, 韩吉田, 赵红霞. 单沉浸管流化床内离散颗粒数值模拟[J]. 浙江大学学报(工学版), 2015, 49(1): 150-156.

REN Libo, HAN Jitian, ZHAO Hongxia. Numerical simulation of discrete particles in fluidized bed with immersed tube[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(1): 150-156.

[7] 李斌, 纪律. 流化床炉内颗粒混合的离散单元法数值模拟[J]. 中国电机工程学报, 2012, 32(20): 42-48.

LI Bin, JI Lü. Numerical simulation of particle mixing in circulating fluidized bed with discrete element method[J]. Proceedings of the CSEE, 2012, 32(20): 42-48.

[8] 纪律. 循环流化床流动及磨损特性的DEM数值模拟[D]. 保定: 华北电力大学, 2011.

[9] LI Tingwen, ZHANG Yongmin, HERNNDEZ-JIMÉNEZ F. Investigation of particle-wall interaction in a pseudo-2D fluidized bed using CFD-DEM simulations[J]. Particuology, 2016, 25: 10-22.

[10] 田凤国, 章明川, 齐永锋, 等. 流化床轴径向混合特性的数值研究[J]. 中国电机工程学报, 2006, 26(21): 119-124.

TIAN Fengguo, ZHANG Mingchuan, QI Yongfeng, et al. A numerical investigation on axial/lateral mixing in fluidized beds[J]. Proceedings of the CSEE, 2006, 26(21): 119-124.

[11] 李斌, 宋小龙. 循环流化床内颗粒混合特性的数值模拟[J]. 动力工程学报, 2013, 33(10): 759-764.

LI Bin, SONG Xiaolong. Numerical simulation on mixing characteristics of particles in circulating fluidized bed[J]. Journal of Chinese Society of Power Engineering, 2013, 33(10): 759-764.

[12] SHARMA A, WANG S B, PAREEK V, et al. CFD modeling of mixing/segregation behavior of biomass and biochar particles in a bubbling fluidized bed[J]. Chemical Engineering Science, 2014, 106: 264-274.

[13] OLAOFE O O, PATIL A V, DEEN N G, et al. Simulation of particle mixing and segregation in bidisperse gas fluidized beds[J]. Chemical Engineering Science, 2014, 108: 258-269.

[14] 朱润孺, 朱卫兵, 邢力超, 等. 矩形喷动床混合特性的三维数值研究[J]. 中国电机工程学报, 2010, 30(17): 12-16.

ZHU Runru, ZHU Weibing, XING Lichao, et al. A three-dimensional numerical investigation on particle mixing characteristics in rectangular spouted beds[J]. Proceedings of the CSEE, 2010, 30(17): 12-16.

[15] ZHANG Yong, JIN Baosheng, ZHONG Wenqi, et al. DEM simulation of particle mixing in flat-bottom spout-fluid bed[J]. Chemical Engineering Research and Design, 2010, 88(5/6): 757-771.

DEM Simulation on Mixing Characteristics of Particles in Double Jets Fluidized Bed

ZHANGJunqiang1,2,JILü2,LIBin1,CHENHaisheng2,BIANYuming1

(1.School of Energy, Power and Mechanical Engineering, North China Electric Power Uninversity,Baodin 071003, Heibei Province, China; 2. Institude of Engineering Themophsics, Chinese Academy of Sciences, Beijing 100190, China)

Combining the discrete element method (DEM) with computational fluid dynamics, and based on Fortran language programming, a gas-solid coupling model was established according to Newton third law to reveal the motion mechanism of particles in the fluidized bed from the micro-level. The mixing degree of particles in different characteristic regions of the bed was quantitatively analyzed using Lacey mixing index, while factors infuencing the mixing characteristics were studied, during which the axial and radial mixing sequence diagram of particles, the gas and particle velocity distribution, as well as the particle mixing index in the entire bed and at different regions of the bed were obtained. Results show that under the action of air jets, the particles get mixed and segregated, and finally achieve dynamic equilibrium. The axial mixing of particles is faster than radial mixing at the same superficial gas velocity. The scale of fountain area increases with rising superficial gas velocity, while the radial diffusion capacity improves, and the axial diffusion capacity lowers.

fluidized bed; axial mixing; radial mixing; discrete element method; mixing index

2016-03-29

国家国际科技合作专项资助项目(2014DFA60600)；国家自然科学优秀青年基金资助项目(51522605)

张俊强(1991-)，男，河北廊坊人，硕士研究生，主要从事强化传热、气固两相流数值模拟等方面的研究. 李 斌(通信作者)，男，副教授，博士，电话(Tel．)：0312-7522197；E-mail：binli_871@163.com．

1674-7607(2017)02-0091-07

TK224

A 学科分类号：470.20