考虑铰链间隙的水面并联稳定平台动力学分析

李豪杰，张合，李珂翔，谢克峰

(1.南京理工大学 智能弹药技术国防重点学科实验室，江苏 南京 210094；2.中国船舶重工集团公司 第724研究所，江苏 南京 210003)

考虑铰链间隙的水面并联稳定平台动力学分析

李豪杰1，张合1，李珂翔2，谢克峰1

(1.南京理工大学 智能弹药技术国防重点学科实验室，江苏 南京 210094；2.中国船舶重工集团公司 第724研究所，江苏 南京 210003)

针对某小型浮式稳定平台结构紧凑、负载惯量大的特点，设计了一种以少自由度并联机构为基础的改进型串联与并联机构。根据该平台的结构特点，进行了运动学分析，推导了系统雅可比矩阵，并利用Lagrange方法建立了平台的动力学模型，分析了平台的动力学特性。为分析含间隙的支链受力，将其简化为刚体—弹簧模型，通过改进的Hertz接触理论，采用非线性弹簧阻尼模型计算接触力，最终建立了含铰链间隙的平台动力学模型。数值计算与实验结果表明了数据建模的有效性，同时铰链间隙对动平台的位置精度和动力学特性产生了显著影响，对平台结构产生了较强的冲击。

机械学；并联机构；稳定平台；铰链间隙；动力学分析

0 引言

工作于水面的小型无人浮式稳定平台，搭载有光电探测设备，因其体积较小、运输方便等优点，在海洋区域侦察等方面具有重要的应用价值。平台性能的优劣决定了探测设备能否正常工作，作为负载的探测设备质量较重，波浪绕动大，平台尺寸有限制，这些特点决定了平台的结构形式必须具有刚度大，承载能力强，动态性能好等特性[1]。并联机构具有上述优点，因而在运动平台领域得到了广泛应用。通常并联机构的设计指标主要为满足大负载和高刚度等要求，故多采用电动缸，驱动能力有限，空间占用大，并且会带来额外负载，因此不适用于本文的稳定平台[2-4]。本文提出一种新型稳定平台，其特点是将滚珠丝杆和大功率电机固定，采用固定长度的支撑杆连接动平台，从而具有空间利用率高和负载能力强等优点。

由于该平台的使用环境与结构特点，机构中的铰链在工作一段时间后，不可避免地会出现间隙，另外加工装配工艺也决定了间隙存在的必然性。相关文献已验证，间隙会导致整个系统的动力学特性存在非线性[5-6]，尤其是当铰链内部在接触和分离两种运动模式之间转换时，会产生强烈碰撞。因此很有必要研究运动副含间隙的并联机构。目前，含间隙连杆机构的研究已取得了较多成果，而含间隙并联机器人的研究仍然很少。Shiau等[7]研究了一种含间隙柔性并联机构的非线性动力学特性；Flores等[8]研究了柱铰对多体系统的影响，建立了平面间隙铰模型。

本文对稳定平台进行运动学分析，得到系统雅可比矩阵；利用Lagrange方法，建立平台的完整动力学模型，通过数值计算得到动力学曲线；以支链间隙为研究对象，利用刚体—弹簧模型简化支链，采用改进的Hertz接触理论、非线性弹簧阻尼模型计算含间隙铰链的接触力，得到含间隙平台动力学方程，并结合实验分析间隙对动力学特性的影响。所得结论可为此类平台的控制应用提供理论参考。

1 稳定平台的结构

1.1 结构与自由度

如图1所示为设计的稳定平台结构原理示意图，其主要构成为动平台、三自由度球铰链、支撑杆、二自由度虎克铰、丝杆螺帽和滚珠丝杆、基座等部件。动平台靠3个支点A1、A2、O分别与平台的基座和传动支链相连接，并构成以O点为直角的等腰直角三角形A1A2O.

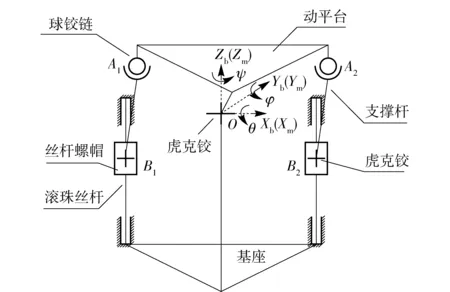
图1 稳定平台原理Fig.1 Schematic diagram of the platform

传动支链由一套滚珠丝杆套件、一个虎克铰链、一个支撑杆和一个球铰链构成。其中，滚珠丝杆固定于基座，只有一个绕其自身回转轴的旋转自由度；丝杆螺帽只有一个沿着丝杆上下移动的平移自由度，该运动受控于滚珠丝杆的旋转运动。球铰链和虎克铰链的几何中心与滚珠丝杆回转轴重合；当动平台与基座两个平面平行时，此3个部件的连线垂直于动平台平面。动平台受O点处的虎克铰链制约，只可作两个自由度的旋转运动。

1.2 坐标系建立

坐标系的建立如图1所示，具体如下：

平台基座坐标系{Cb}：该坐标系固定在稳定平台的下平台基座上，原点O位于直角三角形A1A2O的直角，{Cb}坐标轴Xb、Yb、Zb分别与基座的横轴、纵轴、垂直轴相互平行，其中Zb与基座的垂直轴重合。绕Xb、Yb、Zb3轴的转角分别为θ、φ、ψ. 下文未说明的坐标变换均基于平台基座坐标系。

动平台坐标系{Cm}：该坐标系固定在稳定跟踪平台的动平台上，原点Om外与{Cb}坐标系的原点O重合，当动平台处于平衡位姿时，{Cm}坐标轴(Xm，Ym，Zm)与{Cb}坐标轴(Xb，Yb，Zb)平行。

2 稳定平台的动力学建模

采用Lagrange方法建立整个稳定平台的动力学模型。Lagrange方程可表示为

(1)

2.1 动平台的动能与势能

动平台只有转动自由度，没有平移自由度，刚体的转动动能为刚体的动量矩与角速度点积的一半，则转动动能的矩阵形式为

(2)

式中：mωm代表动平台基于空间角速度矢量，将其转换为欧拉角空间坐标系，转换矩阵为REuler；mIm代表动平台在其自身坐标系中相对惯性主轴的惯量矩阵。

将局部空间向量替换成广义坐标，动能方程可表示为

(3)

2.2 支撑杆及丝杆螺帽的动能与势能

传动支链的动能包括丝杆螺帽、支撑杆的平动动能和转动动能；势能包括两者在平台基座坐标系Z轴方向的势能。把支撑杆简化为直杆，丝杆螺帽和支撑杆质量分别为mz、ms，其质心在动平台与基座保持平行时距动平台球铰链Ai的距离分别为d2、d1.

(4)

式中：

JVA=ROA·REuler,

(5)

ROA表示动平台上的球铰链Ai相对于动平台坐标系的位置向量，REuler表示欧拉转换坐标系；JInv为系统的雅可比矩阵。

支撑杆的转动动能为

(6)

式中：bIms为支撑杆在其自身坐标系中的转动惯量矩阵；L为连杆长度。

支撑杆的平动动能为

(7)

支撑杆的势能为

Vms=msg[1 1]·bPmsZ，

(8)

式中：bPmsZ=[bPms1Z，bPms2Z]T为所有支撑杆在平台基座坐标系中Z轴的坐标。

丝杆螺帽的动能为

(9)

丝杆螺帽的势能为

Vmz=mzg[1 1]·bPmzZ,

(10)

式中：bPmzZ=[bPmz1Z，bPmz2Z]T为所有丝杆螺帽在平台基座坐标系中Z轴的坐标.

2.3 动力学方程

综合以上各式，则有理想约束平台动力学方程为

(11)

3 含间隙传动支链建模

3.1 广义力分析

图2为含间隙传动支链受力模型示意图，CiDi为支撑杆，AiCi为球铰链，BiDi为虎克铰，后二者间存在铰链间隙。由于含间隙铰链是支链的薄弱环节，所以在受力分析时，将支撑杆看作刚体，铰链简化为弹簧。由于间隙相对于平台仍是极小量，所以假设间隙不改变支链的宏观位姿关系。fCi与fDi为施加于支撑杆两端的铰链接触反力。根据力与力矩平衡原理可得

fCi+fDi+m1g=m1amsi,

(12)

d1LifCi+(d1-L)LifDi+Msi=bImsiαmsi,

(13)

式中：asi为支撑杆质心的加速度；αsi为支撑杆的角加速度；Msi为虎克铰Bi限制支撑杆轴向旋转的力矩。对于铰链接触力有

fCi=ks(Ai-Ci)+cs(VAi-VCi),

(14)

fDi=kr(Bi-Di)+cr(VBi-VDi),

(15)

式中：ks、cs为球铰的刚度、阻尼系数；kr、cr为虎克铰的刚度、阻尼系数。对于动平台有

(16)

图2 含间隙传动支链受力示意图Fig.2 Force diagram of chain with clearance joints

3.2 含间隙球铰的数学模型

根据实验测得，球铰间隙在支链中最大，以其为例分析。如图3所示，α和β分别代表球窝、球头，其半径分别为Rα、Rβ. 球铰间隙定义为c=Rα-Rβ，Pα(Ci)、Pβ(Ai)分别为球窝、球头的中心，球窝、球头中心分别在自身坐标系中的矢径为rPα、rPβ.

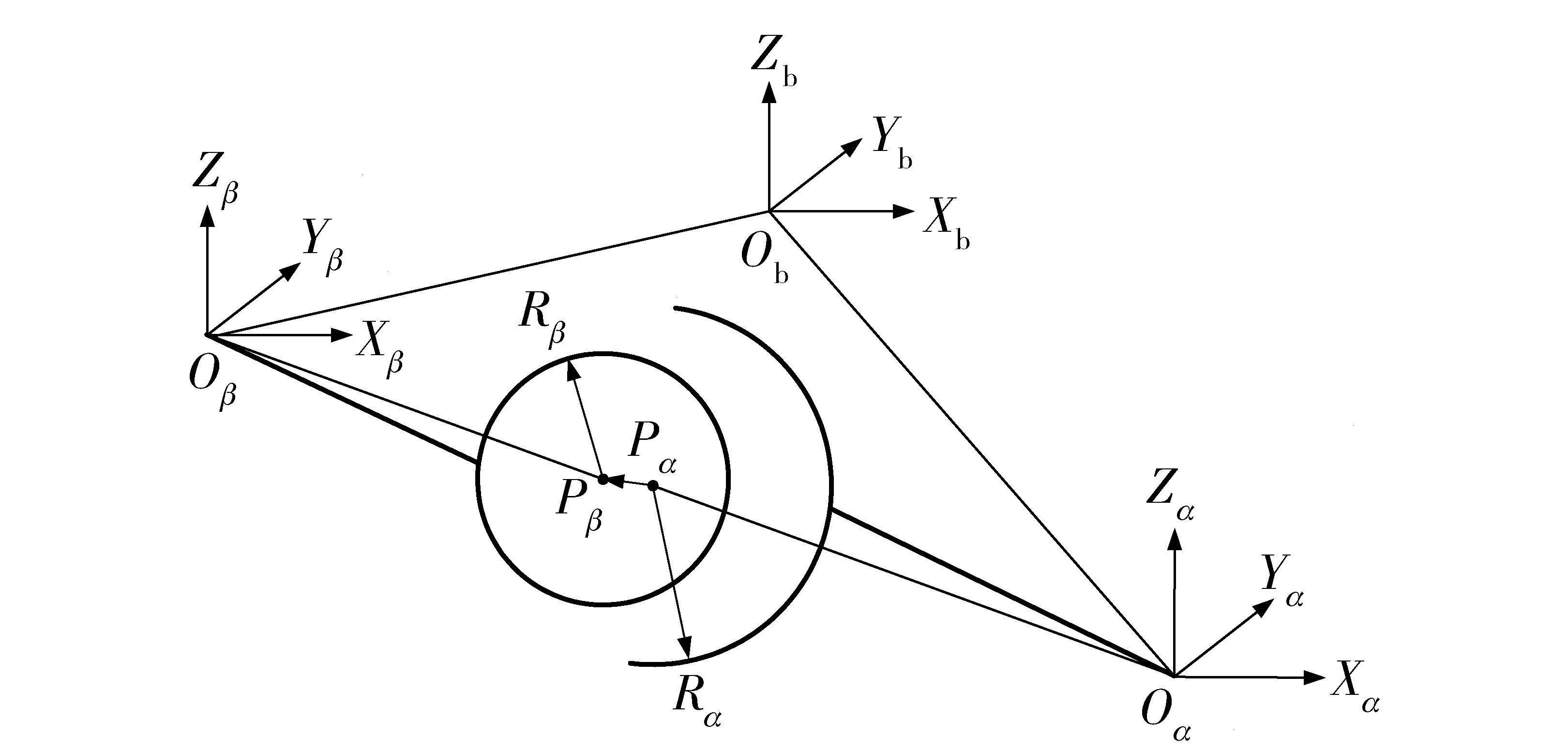
图3 含间隙球铰示意图Fig.3 Schematic diagram of spherical joint with clearance

则其在基座坐标系中的矢径为

(17)

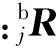
(18)

球窝与球头接触的几何条件则可定义为

δi=ei-c=|AiCi|-c.

(19)

含间隙球铰的运动状态分为自由运动和接触变形，在运动过程中存在能量损耗，不能用完全弹性碰撞建模；采用Machado等[9]扩展后的Hertz接触模型，使用非线性弹簧阻尼模型描述接触力，其中法向接触力为

(20)

(21)

(22)

根据Coulumb摩擦模型[10]，切向接触力为

FiT=-μsFiNviT/|viT|,

(23)

式中：viT为接触点相对滑动线速度；μs为动摩擦系数。则球铰接触力合力为

fCi=FiN+FiT.

(24)

3.3 含间隙动力学模型

含间隙铰链在分离状态和接触变形状态之间转换，可用(24)式导出的非线性弹簧阻尼力代替铰链约束力，则系统的非线性动力学方程[8]为

(25)

式中：M为广义质量矩阵；Q为广义力；Φ(q,t)=0为理想铰链约束方程；Φq为约束方程的雅可比矩阵；λ为拉格朗日乘子；Fc=[fC1，fC2]T为接触力相对广义坐标q的广义接触力，包括法向接触力和切向接触力，当铰链处于分离状态时，Fc=0.

4 仿真分析与实验

为了验证平台设计是否满足要求，研究平台的动力学特性与铰链间隙的影响，给定动平台在垂直面内的激励力为80sin (20πt) N·m. 算例采用Newmark算法进行计算，根据(25)式，计算得到了动平台受间隙影响的位移曲线，以及铰链接触力的变化曲线，如图4、图5所示。

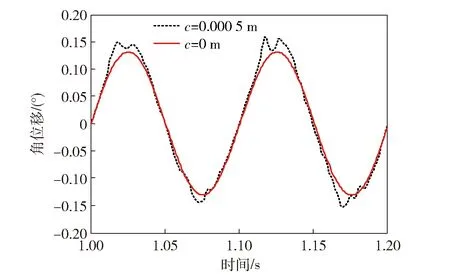
图4 含间隙平台φ角位移曲线Fig.4 Displacement curves of angle φ of platform with clearance joints

图5 球铰B2接触力曲线Fig.5 Contact force curves of spherical joint B2

由图4可知，在计入球铰间隙后，动平台的摆动幅度增大了10%左右，在峰值附近存在了多个紧靠的尖峰，说明球铰内部发生了连续的碰撞，快速地在接触变形和自由运动状态之间转换。根据图5可知，球铰接触力峰值非常大，在没有考虑间隙时，接触力是一条平滑的曲线，计入球铰间隙后是理想接触时的40倍；峰值相对集中，说明球铰内部存在有规律的碰撞，这也印证了图5的多次连续碰撞现象；峰值集中的区域即为平台换向的时刻，对于平台的稳定调平控制，需要频繁地在平衡位置附近换向，间隙的存在无疑给系统增加了迟滞环节，放大了误差，这种影响也体现在了样机调试实验中。

完成的平台原理样机如图6所示，支撑杆两端的球铰和虎克铰随着使用时间的增长，在原有小间隙的基础上不断变大，对系统产生的影响也会越来越大，样机中的球铰分别为使用3个月后具有一定间隙的状态和减小间隙改进后的全新状态。

图6 稳定平台样机Fig.6 Experimental platform prototype

在测试时，并联稳定平台驱动电机位置锁死，负载设备在OXZ平面内快速运动，对动平台施加激励力，并采用高带宽的惯性姿态参考模块测量动平台的角度，铰链间隙的受力较难通过压力测出，因此采用角度测量进行间接说明。图7(a)为使用后球铰角位移实验值与仿真数据对比曲线，图7(b)为采用改进的小间隙铰链与原有使用磨损一段时间的铰链进行对比的角位移实验曲线。对动平台角位移进行了6次测量，测试数据见表1.

由图7(a)可知，实验数据与仿真结果具有较好的一致性，说明了数据建模的有效性，由图7(b)可知，经过球铰间隙的影响，动平台的角位移被放大，其误差幅度由表1可知最大误差为30.4%，可知因间隙导致的冲击使得相关机构产生了更大的弹性变形，从而使误差进一步放大。通过球铰改进，动平台的角位移保持在0.15°内，能在一定程度上减小球铰间隙的影响。

表1 使用后状态与改进后状态铰链下的平台角位移误差Tab.1 Angular displacement errors of platform with used and improved hinges

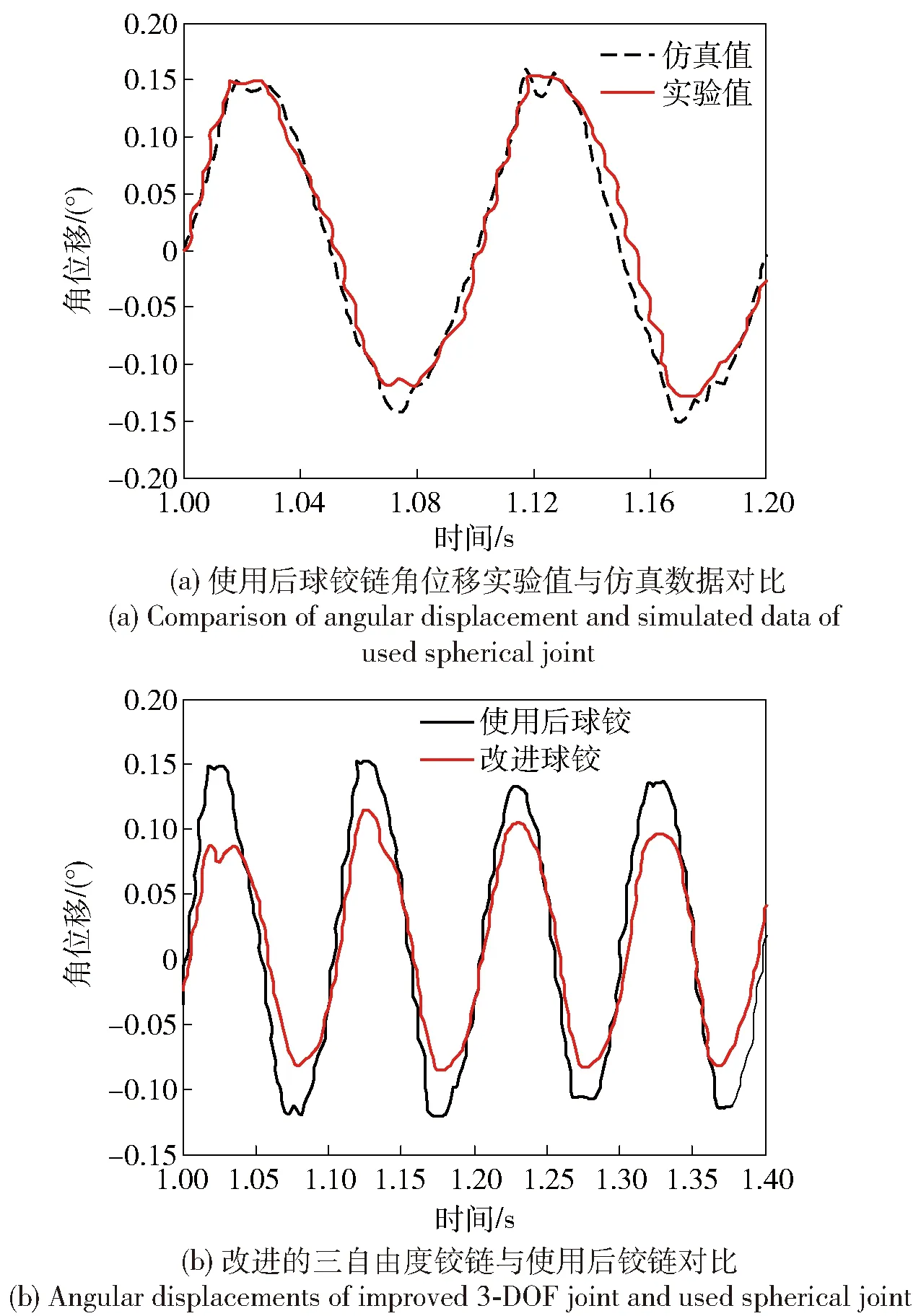
图7 动平台摇摆模拟实验角位移对比曲线Fig.7 Simulated and experimental angular displacements of platform

5 结论

本文针对某小型浮式稳定平台的需求，设计了一种以少自由度并联机构为基础的改进型串并联机构。对该平台进行了运动学分析，推导了系统雅可比矩阵，建立了动力学模型。通过将支链简化为刚体—弹簧模型，建立了含铰链间隙的平台动力学模型。数值计算与实验结果表明：数据建模与实验结果具有较好的一致性，说明了数据建模的有效性；间隙会导致动平台在换向时出现约为30.4%的位移误差，此时由于铰链在自由运动与接触变形之间反复转换状态，产生了最大值比理想接触力峰值高40倍的接触力，给系统带来了强烈的非线性扰动。在已知这些结果后，通过结构抑制和算法补偿是修正此类扰动的有效途径。所得结论可为该类平台的高精度控制与结构优化设计提供理论依据。

References)

[1] 阴蕊，房建成，钟麦英. 航空遥感用三轴惯性稳定平台动力学建模与仿真[J]. 中国惯性技术学报，2011，19(6)：676-680，685. YIN Rui, FANG Jian-cheng, ZHONG Mai-ying. Dynamic modeling and simulation of inertial stabilized platform for aerial remote sensing system[J]. Journal of Chinese Inertial Technology, 2011, 19(6): 676-680,685. (in Chinese)

[2] Zhang Y B, Liu H Z, Wu X. Kinematics analysis of a novel parallel manipulator[J]. Mechanism and Machine Theory, 2009, 44(9)：1648-1657.

[3] 牛雪梅，高国琴，刘辛军，等. 新型驱动冗余并联机构动力学建模及简化分析[J]. 机械工程学报，2014，50(19)：41-49. NIU Xue-mei, GAO Guo-qin, LIU Xin-jun, et al. Dynamic formulation and simplified model of a novel 3-DOF parallel mechanism with actuation redundancy [J]. Journal of Mechanical Engineering, 2014, 50(19): 41-49. (in Chinese)

[4] 满益明，陈慧岩，胡玉文，等. 智能车辆捷联视线稳定跟踪平台设计与实现[J]. 中国惯性技术学报，2009，17(4)：397-402. MAN Yi-ming, CHEN Hui-yan, HU Yu-wen, et al. Design and implementation of intelligent vehicle strapdown line-of-sight stabilization pointing platform system [J]. Journal of Chinese Inertial Technology, 2009, 17(4): 397-402. (in Chinese)

[5] Zhang X C, Zhang X M. A comparative study of planar 3-RRR and 4-RRR mechanisms with joint clearances [J]. Robotics and Computer-Integrated Manufacturing, 2016, 40：24-33.

[6] Ma J, Qian L F, Chen G S, et al. Dynamic analysis of mechanical systems with planar revolute joints with clearance [J]. Mechanism and Machine Theory, 2015, 94: 148-164.

[7] Shiau T N, Tsai Y J, Tsai M S. Nonlinear dynamic analysis of a parallel mechanism with consideration of joint effects [J]. Mechanism and Machine Theory, 2008, 43(4): 491-505.

[8] Flores P, Ambrosio J. Revolute joints with clearance in multibody systems[J]. Computers and Structures, 2004, 82(17/18/19): 1359-1369.

[9] Machado M, Moreira P, Flores P, et al. Compliant contact force models in multibody dynamics: evolution of the Hertz contact theory [J]. Mechanism and Machine Theory, 2012, 53: 99-121.

[10] Flores P, Ambrósio Ambrosio J, Claro J C P, et al. A study on dynamics of mechanical systems including joints with clearance and lubrication [J]. Mechanism and Machine Theory, 2006, 41(3): 247-261.

Dynamic Analysis of Offshore Parallel Stabilized Platform in Considering Joint Clearance

LI Hao-jie1, ZHANG He1, LI Ke-xiang2, XIE Ke-feng1

(1.Ministerial Key Laboratory of ZNDY, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China；2.No.724 Research Institute, China Shipbuilding Industry Corporation, Nanjing 210003, Jiangsu, China)

An improved serial-parallel mechanism based on less DOF parallel mechanism is designed for a floating stabilized platform with compact structure and high load inertia. Based on the structural characteristics of the platform, the kinematics is analyzed, the system Jacobian matrix is derived, and a dynamic model is established and analyzed by using Lagrange equation. A simplified rigid body-spring model is proposed to analyze the chains with clearance joints. A non-linear spring-damper model is introduced to calculate the contact force by using improved Hertz contact theory, and a dynamic model considering joint clearance is established. The numerically computated and experimental results show that the dynamic model is effective, and the clearance has significant impact on the structure,position accuracy and dynamic characteristics of moving platform.

mechanics; parallel mechanism; stabilized platform; joint clearance; dynamic analysis

2016-04-07

国家自然科学基金项目(51475243)

李豪杰(1973—)，男，副教授，硕士生导师。E-mail:haojieli@njust.edu.cn

TP242.3

A

1000-1093(2017)01-0129-06

10.3969/j.issn.1000-1093.2017.01.017