弹壳体结构对燃料装药抛撒速率影响的数值模拟研究
2017-02-20王晔白春华李建平
王晔,白春华,李建平
(北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
弹壳体结构对燃料装药抛撒速率影响的数值模拟研究
王晔,白春华,李建平
(北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
为研究壳体结构对燃料近区抛撒速率的影响,利用LS-DYNA程序,分别对无加强杆结构和有加强杆结构的中心抛撒药驱动燃料抛撒和壳体破坏过程进行数值模拟,并与试验结果进行了对比,得到了燃料边界初始膨胀状态、壳体破裂过程和刻槽应力随时间变化的规律,以及不同结构对燃料抛撒最大速率的影响。研究结果表明:在满足结构强度的要求且径向强度相同的情况下,加强壳体的轴向拉力,能够有效提高燃料抛撒速率;在相同的中心药量/燃料量的情况下进行抛撒,当轴向拉力提高0.7×106N时,有加强杆结构较无加强杆结构有利于获得较大的抛撒速率,有加强杆结构的燃料最大抛撒速率可达316.3 m/s,无加强杆结构的燃料最大抛撒速率为285.3 m/s,燃料抛撒最大速率提高了10.8%.
兵器科学与技术;有加强杆结构;无加强杆结构;抛撒速率;数值模拟
0 引言
在驱动载荷作用下的燃料抛撒技术[1-4],目前广泛应用于消防、煤矿、化工、烟花爆竹和军事等领域,如灭火弹、爆破除尘和燃料空气炸药、烟花燃放等。为了在不同场合应用,通常需要将被抛撒物质置于固定的容器中,便于储存、运输和使用。为此世界各国学者开展了燃料空气混合物形成过程的相关研究。
被抛撒物作为最终的考察和分析对象,无论是研究爆轰驱动平板飞片的运动特性试验[5-7]和数值计算[8-11],或是探讨球形金属颗粒抛撒规律的最初阶段,均需要考虑并设计合理的壳体(容器)结构[12]。从起爆到壳体膨胀、破裂为破片的过程,以及燃料抛撒、破碎、雾化的过程,是爆轰驱动燃料抛撒的两个外在表现形式。相同中心药/燃料量的装药结构,在形成扁平状的云雾形态时,可以达到最强的破坏效应[13]。另有研究者研究发现,覆盖范围越广且贴在地面上的扁平状云雾点爆后,其破坏效应较强[14],因此学者们[15-22]利用实验室等效试验和数值模拟技术,对控制燃料抛撒形成扁平状云雾的技术开展了一系列的研究。研究结果表明,壳体的破裂过程直接影响到燃料的分散状态,因此只有合理的壳体结构才能达到预期目的。其中壳体轴向约束拉力的改变,对燃料抛撒速率的影响较为关键。
本研究针对无加强杆结构和有加强杆结构,在中心抛撒药驱动下,对燃料的抛撒初始速率和壳体破坏的过程进行数值模拟,并在试验结果对比的基础上,分析了两种结构对燃料抛撒的影响规律。
1 结构模型
有无加强杆结构和有加强杆结构两种壳体结构。无加强杆结构由中心管、上下加强端板以及筒壁组成,而有加强杆结构在无加强杆结构的基础上,增加加强杆,对称分布在筒壁内部。在筒壁上均匀分布深度为0.6 mm的16道刻槽;上下端板为圆形截面,直径为370 mm;筒壁为长度1 150 mm的柱形。内部装填125 kg混合燃料,中心管内部装填1.08 kg TNT,作为中心抛撒药。结构与尺寸如图1所示。

图1 两种结构模型尺寸Fig.1 Geometric models
2 模拟参数
2.1 计算模型
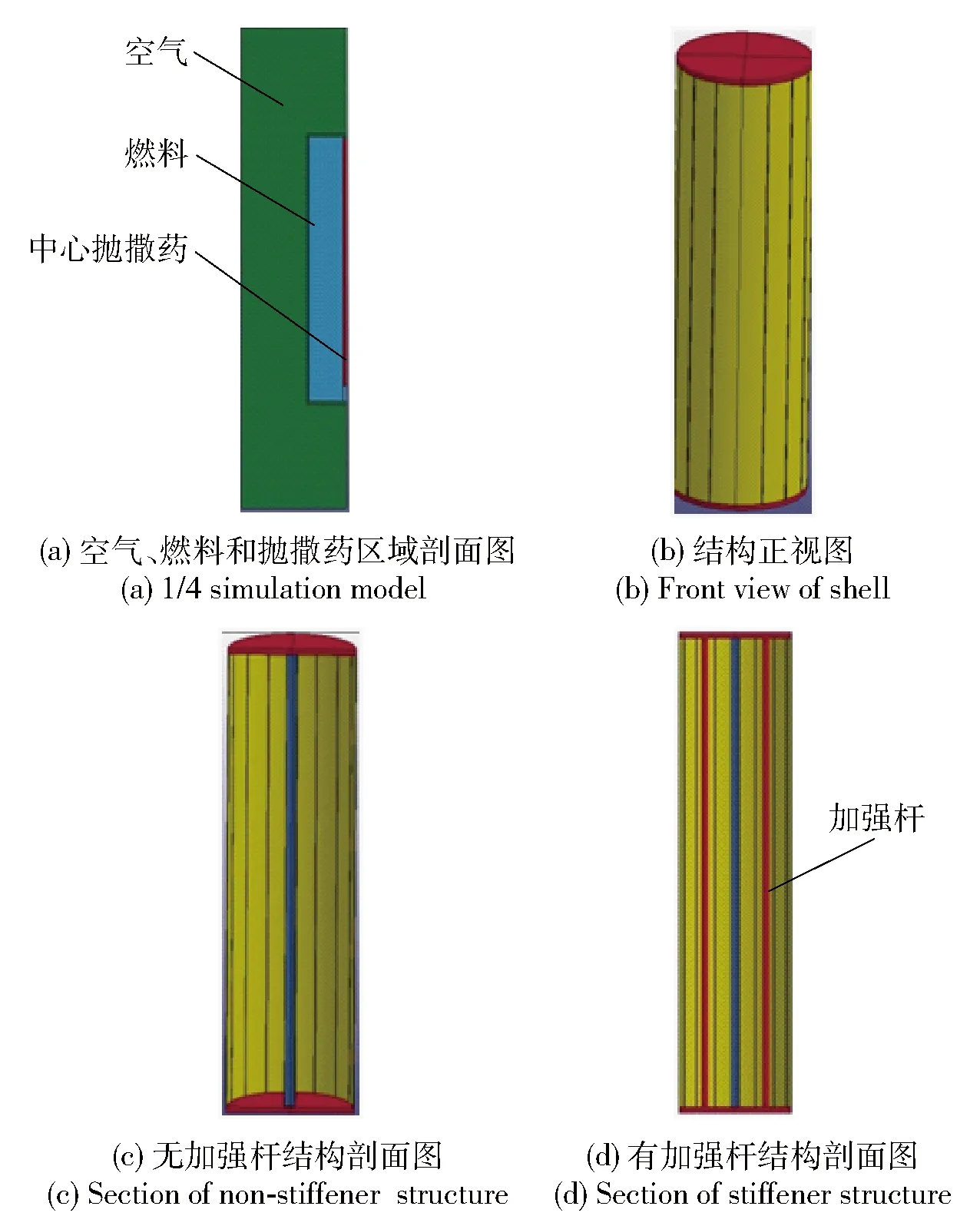
图2 无加强杆结构和有加强杆结构的计算模型Fig.2 Computation models for different structures
按照图1所示尺寸,进行1∶1建模。空气区域尺寸为1 m×1 m×2 m,两种结构的计算模型如图2所示。
2.2 计算方法
计算方法采用流体- 固体耦合算法,单元采用单点积分的ALE多物质单元,研究壳体破裂情况以及燃料抛撒状态。中心抛撒药、燃料和空气区域采用Euler网格,壳体各结构采用Lagrange网格。由于两种结构为轴对称结构,为了节省运算时间,采用1/4模型进行计算分析。
2.3 材料参数
2.3.1 中心抛撒药
利用MAT_HIGH_EXPLOSIVE_BURN材料模型和选用JWL状态方程进行描述中心抛撒药,抛撒药
选用TNT,主要材料计算参数如表1[9]所示。JWL状态方程形式为
(1)
式中:p为爆轰产物的压力;V是相对比体积;e是单位体积炸药的内能;A、B、R1、R2、ω均为JWL状态方程参数。
2.3.2 燃料
为便于分析,混合燃料用水代替。燃料模型采用MAT_NULL材料模型和Gruneisen状态方程进行描述,主要参数见表2所示。Gruneisen状态方程形式为

表1 抛撒药的主要计算参数Tab.1 Computation parameters of central high-explosive
注:ρ为质量密度,D为爆轰速度。
(2)
式中:C是冲击波传播速度;γ0是Gruneisen指数;α是γ0的一阶体积修正量;μ=(ρ/ρ0)-1,ρ0为燃料初始质量密度;S1、S2、S3为Gruneisen状态方程的系数。

表2 燃料的基本计算参数Tab.2 Parameters of fuel
2.3.3 空气
空气采用MAT_NULL材料模型和线性多项式LINEAR_POLYNOMIAL状态方程,主要计算参数如表3所示。状态方程表达形式为
p=c0+c1μ+c2μ2+c3μ3+
(c4+c5μ+c6μ2)e,

2.3.4 结构材料
壳体结构选用PLASTIC_KINEMATIC材料模型,该模型可较为准确地模拟壳体在爆炸过程中发生的弹性变形、塑性变形以及破裂等过程。各结构主要材料参数如表4所示。

表3 空气的基本计算参数Tab.3 Computation parameters of air

表4 壳体的计算参数Tab.4 Parameters of components
注:E为弹性模量,υ为泊松比,σs为屈服应力,Et为屈服段模量,δ为失效应变量。
2.3.5 初始条件和边界条件
初始条件:为了更真实地模拟该装置的初始作用过程,采用一端起爆,即下端中心起爆方式。
边界条件:由于壳体外部为无限边界的空气,故边界条件采用无反射边界条件。
2.3.6 网格的选取和计算时长
终止计算条件由计算时间决定,计算时间为2 ms,当抛撒时间到达2 ms时停止计算。每隔10 mm对1/4模型进行映射网格划分,体单元形状为六面体。模型总计算时长约为15 h.
3 模拟结果分析讨论
3.1 壳体破裂过程
由于壳体破裂的先后顺序,直接影响燃料抛撒的形态变化,因此壳体破裂过程的结果如图3所示。从图3中观察到:在0~1 ms之间时,两种结构由于中心药爆轰作用,筒壁由下向上进行膨胀,刻槽由于强度较弱首先破裂失效,导致筒壁开裂,两种结构筒壁均形成条状破片;当在1~2 ms之间时,筒壁破片与上下端板脱离,向四周运动,此时,无加强杆结构的部件均已失效,而有加强杆结构上下端板之间的约束依然存在。显然,产生这种区别的原因是有加强杆结构具有加强杆,使得整个结构的抗轴向拉力能力增强,导致爆轰作用力集中在径向,使得筒壁快速破裂,导致有杆加强结构的筒壁破裂较无加强杆结构筒壁破裂更彻底。
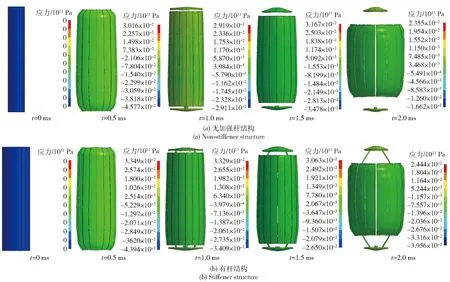
图3 壳体应力的数值模拟结果Fig.3 Simulated results of shell stress
3.2 刻槽单元应力分析
已有研究[9]表明轴向中部横截面的燃料抛撒效果最为显著,且具有对称性,因此选择中部横截面为观察面,即选择距离下端板底端525 mm处的刻槽单元为监测点,刻槽单元应力随时间变化的结果如图4所示。从图4中可以看出:两种结构的应力变化趋势相同,均表现为随时间单调增加;随着时间的增加,刻槽应力达到最大值时,爆轰波峰值超压超过刻槽破裂临界应力后,刻槽破裂,应力迅速减小至0 GPa,此时,看作燃料开始抛撒。

图4 壳体刻槽位置单元的应力时程曲线Fig.4 Stress of cutting cells versus time
根据牛顿第三定律,随着驱动力的不断增加,刻槽约束应力也在不断增加,最终达到壳体刻槽破裂应变量临界值,导致壳体约束应力失效。从图4 可以看出,有加强杆结构失效时间为0.44 ms,而无加强杆结构失效时间为0.49 ms. 其原因是:在相同的驱动力作用下,强度较弱的地方先破裂。在无加强杆结构中,其轴向拉力小于有加强杆结构的轴向拉力;在有加强杆结构中,加强杆部件增大了轴向约束力,使得径向拉力弱于轴向拉力,在筒壁结构相同的情况下,使得驱动力的作用力集中在径向筒壁的拉伸,因此导致有加强杆结构的刻槽应力失效时间早于无加强杆结构的刻槽应力失效时间。
3.3 燃料水平抛撒速率
两种结构均为圆柱筒壁,所以在径向方向的约束力相等,而轴向方向约束力由于部件的差异导致不同。在进行轴向约束计算时,两种结构的差异在加强杆部件,因此两种结构的约束力差值就是加强杆部件的约束力,约束力[23]差值为
W=d2σa/2,
(4)
式中:W为约束力;d为加强杆截面直径,d=0.018 m;σa为屈服强度,由于加强杆部件材料为30CrMnSiA圆钢材料,则σa=1 080 MPa.
根据(4)式,则轴向约束力差值ΔW=4W=0.7×106N. 可见,两种装置结构强度只在轴向方向上相差0.7×106N.

图6 有加强杆结构燃料抛撒试验的结果Fig.6 Experiment results of fuel dispersion for stiffener structures
选择中部横截面为观察面,即选择距离下端板底端525 mm处的燃料抛撒单元为监测点,不同结构燃料中部横截面抛撒速率随时间变化的结果如图5所示。由图5可知,两种结构在燃料速率呈现相似的变化规律,变化主要为先快速上升,后下降、振荡,再逐渐上升的趋势。在中心抛撒药爆轰作用下,燃料由静止状态开始加速,抛撒速率快速上升;壳体受到应力波冲击并破裂,燃料喷射到空气中,受到空气阻力作用,燃料速率进入减速阶段;随着中心抛撒药产生的爆轰产物向外扩散推动燃料,燃料速率又有所上升。有加强杆结构的燃料抛撒速率大于无加强杆结构。有加强杆结构的燃料最大抛撒速率可达316.3 m/s,而无加强杆结构的燃料最大抛撒速率为285.3 m/s,二者相差31.0 m/s,燃料抛撒最大速率提高了10.8%. 这是由于有加强杆结构的轴向约束力大于无加强杆结构,使得径向刻槽应力失效时间早于无加强杆结构的刻槽应力失效时间,阻力时间作用较短,使得燃料加速充分,获得较大的初始速率。
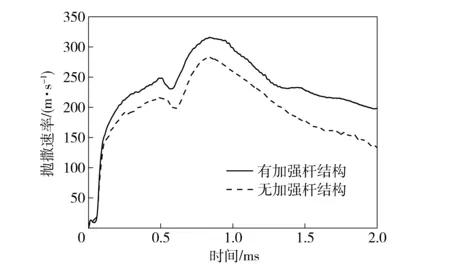
图5 不同结构燃料抛撒速率的时程曲线Fig.5 Initial dispersing velocities of two types of shells versus time
3.4 模拟与试验验证
为了验证模拟结果,进行燃料抛撒试验。试验中采用有加强杆壳体结构(见图1(b))。将壳体垂直摆放在试验架上,下端板距离地面高度为1.5 m. 摆放位置作为爆心,以爆心作为原点,距离爆心为15 m处布置两对标志杆,用来读取燃料抛撒半径,进而得到抛撒速率。高速摄影仪垂直于标志杆布置,型号为V12,分辨率为1 280×800,拍摄速度为2 000帧/s.
图6为试验记录到的燃料抛撒过程。由起爆后记录的时刻云雾形状看,结构变形及破裂情况模拟结果与实际相一致。
将燃料抛撒初始速率与试验结果进行对比,如表5所示。虽然燃料抛撒初始抛撒速率的数值模拟结果和试验结果之间存在误差,但是计算值与试验结果在燃料抛撒前期的总体趋势一致,显然到2 ms时速率误差较大。因此,需要将总计算时间控制在壳体破坏前的2 ms时间内,模拟结果与试验结果较为相符。

表5 燃料抛撒初始抛撒速率的计算结果与试验值对比Tab.5 Calculated and experimental results at the same time
燃料抛撒初始速率的数值模拟和试验结果之间存在误差是由于以下3点造成的:1)计算中采用水的状态模型代替了试验中使用的燃料,因此导致二者在壳体破裂的均匀性方面略有差异;2)在运用有限元分析方法来进行计算时,方法本身存在计算误差;3)试验装置本身存在的工艺误差,以及记录设备的精度和记录的同步误差。
4 结论
本文基于中心抛撒药、燃料以及壳体结构的数值模拟仿真模型,对有加强杆结构和无加强杆结构的壳体进行数值研究,得到如下结论:
1)有加强杆结构较无加强杆结构有利于获得较大的抛撒速率,有加强杆结构的燃料最大抛撒速率可达316.3 m/s,而无加强杆结构的燃料最大抛撒速率为285.3 m/s.
2)有加强杆结构较无加强杆结构具有较强的轴向拉力,在相同的中心药量/燃料量的情况下进行抛撒,当轴向拉力提高0.7×106N时,燃料抛撒最大速率提高了10.8%.
采用数值模拟仿真模型对燃料边界初始膨胀状态、壳体破裂情况以及最大抛撒速率进行模拟分析,模拟结果与试验燃料抛撒初期形状吻合较好,可为壳体结构的设计提供参考依据。
References)
[1] 国家煤矿安全监察局事故查询系统[DB/OL]. http:∥media.chinasafety.gov.cn:8090/isystem/shigumain.jsp. Accident inquiry system of national coal mine safety supervision bureau[DB/OL]. http:∥media.chinasafety.gov.cn:8090/isystem/shigumain.jsp.(in Chinese)
[2] 张国顺. 中国兵器工业安全生产50年[J].兵工安全技术, 2000(2): 5-9. ZHANG Guo-shun. The safe production of China’s weapons industry in 50 years[J]. Ordnance Safety Technology, 2000(2):5-9. (in Chinese)
[3] 王莹, 马富学. 新概念武器原理[M]. 北京:兵器工业出版社, 1997:485-488. WANG Ying, MA Fu-xue. The theory of new concept weapon[M]. Beijing: Publishing House of Ordnance Industry, 1997:485-488. (in Chinese)
[4] Rao A A. Fuel air explosives[J]. Defence Science Journal, 1987, 37(1):23-28.
[5] Liu G, Hou F, Cao B, et al. Experimental study of fuel-air explosive[J]. Combustion, Explosion and Shock Waves, 2008, 44(2): 213-217.
[6] Zhang Q, Bai C H, Dang H Y, et al. Critical ignition temperature of fuel-air explosive[J]. Defence Science Journal, 2004, 54(4):469-474.
[7] Apparaoa A, Rao C R, Tewari S P. Studies on formation of unconfined detonable vapor cloud using explosive means[J]. Journal of Hazard Material, 2013, 254/255:214-220.
[8] Qi Z, Kezhen W, Aimin L, et al. Numerical simulation on dispersal character of fuel by central HE[J]. Defence Science Journal, 2007, 57(4):425-433.
[9] 陈明生, 白春华, 李建平. 燃料抛撒的初始速率与结构动态响应数值模拟[J].含能材料, 2015, 23(4):323-329. CHEN Ming-sheng, BAI Chun-hua, LI Jian-ping. Simulation on initial velocity and structure dynamic response for fuel dispersion[J]. Chinese Journal of Energetic Materials, 2015, 23(4):323-329.(in Chinese)
[10] 李建平, 白春华, 郭昭平. 云爆装置初始作用过程数值模拟[J]. 弹箭与制导学报, 2009, 29(5):123-125. LI Jian-ping, BAI Chun-hua, GUO Zhao-ping. Numerical simulation of the initial interaction process of FAE device[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(5):123-125.(in Chinese)
[11] 王飞, 白春华, 闫华. 壳体厚度对大口径FAE战斗部效应仿真研究[J]. 弹箭与制导学报, 2003, 23(3):110-112. WANG Fei, BAI Chun-hua, YAN Hua. The study for the effect of the thickness of cylindrical shell on the fuel dispersing in the FAE warhead design by simulation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2003, 23(3):110-112.(in Chinese)
[12] Liu Q M, Bai C H. Research on the explosion temperature response of fuel air explosive measured by colorimetric pyrometer[J]. Journal of China Ordnance, 2010, 6(1):59-64.
[13] Leyer J C. An experimental study of pressure fields by exploding cylindrical clouds[J]. Combustion & Flame, 1982, 48(3):251-263.
[14] Fishburn B, Slagg N, Lu P. Blast effect from a pancake shaped fuel drop-air cloud detonation(theory and experiment)[J]. Journal Hazard Material, 1981, 5(1/2):65-75.
[15] 李斌, 解立峰, 韩志伟, 等.激波驱动下固体颗粒抛撒的实验研究[J]. 实验力学, 2012, 27(6):715-720. LI Bin, XIE Li-feng, HAN Zhi-wei, et al. Experimental study of solid particles dispersal induced by shock wave[J]. Journal of Experimental Mechanics, 2012, 27(6):715-720.(in Chinese)
[16] 闫华, 张奇, 白春华. 发射过载条件下燃料应力状态的数值计算[J]. 兵工学报, 2005, 26(5): 609-614. YAN Hua, ZHANG Qi, BAI Chun-hua. Numerical simulation for stress in fuel under launching over loading[J]. Acta Armamentarii, 2005, 26(5):609-614.(in Chinese)
[17] 丁珏, 刘家骢. 液体燃料爆炸抛撒和FAE 形成过程的数值模拟[J]. 南京理工大学学报, 2000, 24(2):168-171. DING Jue, LIU Jia-cong. Numerical simulation on the process ofexplosive dispersal for forming FAE cloud[J]. Journal of Nanjing University of Science and Technology, 2000, 24(2):168-171.(in Chinese)
[18] 李斌, 解立峰, 倪欧琪, 等. 燃料液滴云雾爆轰特性研究[J]. 弹道学报, 2010, 22(2):90-93. LI Bin, XIE Li-feng, NI Ou-qi, et al. Study on detonation characteristics of fuel drops cloud[J]. Journal of Ballistics, 2010, 22(2):90-93.(in Chinese)
[19] 沈晓波, 鲁长波, 李斌, 等, 液体燃料云雾爆轰参数实验[J].爆炸与冲击, 2012, 32(1):108-112. SHEN Xiao-bo, LU Chang-bo, LI Bin, et al. An experimental study of detonation parameters of liquid fuel drops cloud[J]. Explosion and Shock Waves, 2012, 32(1):108-112.(in Chinese)
[20] 李席, 王伯良, 韩早, 等. 液固复合FAE 云雾状态影响因素的试验研究[J]. 爆破器材, 2013, 42(5): 23 -26. LI Xi, WANG Bo-liang, HAN Zao, et al. Experimental study on influencing factors of the cloud status of liquid-solid fuel air explosive[J]. Explosive Materials, 2013, 42(5):23-26.(in Chinese)
[21] 李斌, 解立峰, 韩志伟, 等.激波作用下水膜变形和雾化实验研究[J]. 实验力学, 2011, 26(4):464-470. LI Bin, XIE Li-feng, HAN Zhi-wei,et al. Study on water films induced by shock wave[J]. Journal of Experimental Mechanics, 2011, 26(4):464-470.(in Chinese)
[22] 薛社生, 刘家骢, 秦承森, 等. 燃料爆炸抛撒成雾的实验与数值研究[J]. 爆炸与冲击, 2001, 21(4): 272-276. XUE She-sheng, LIU Jia-cong, QIN Cheng-sen, et al. Experimental and numerical investigation on explosive dispersal and cloud forming[J]. Explosion and Shock Waves, 2001, 21(4):272-276. (in Chinese)
[23] 祝燮权. 实用五金手册[M]. 上海:上海科学技术出版社, 2000. ZHU Xie-quan. Practical hardware manual[M]. Shanghai: Shanghai Scientific & Technical Publishers, 2000. (in Chinese)
Influence of shell Structure on Dispersing Velocity of Fuel-air Mixture
WANG Ye,BAI Chun-hua,LI Jian-ping
(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)
In order to study the dispersal characteristics for different shell structures, the processes of fuel dispersion and shell breakage driven by central explosive are simulated by LS-DYNA code, and the simulated and experimental results are compared. The boundary expansionstate of fuel and the process of shell breakage are obtained. The variation of cutting force with time and the maximum dispersing velocity of different shell structures are analyzed. Results show that the dispersing velocity of fuel could be effectively increased by enhancing the axial tension while satisfying the structural strength and the same radial strength. When axial tension is up to 0.7×106N, the greater dispersing velocity could be produced by stiffener structure. The maximum dispersing velocity of non-stiffener structure is 285.3 m/s. The maximum dispersing velocity of stiffener structure is 316.3 m/s, that could be increased by 10.8% with the same dose for non-stiffener structure.
ordnance science and technology; stiffener structure; non- stiffener structure; dispersal velocity; numerical simulation
2016-03-23
国家部委预先研究项目(9140A05080507)
王晔(1986—),女,博士研究生。E-mail: wangye_0422@126.com
白春华(1959—),男,教授,博士生导师。E-mail:chbai@bit.edu.cn
TJ410.3+3
A
1000-1093(2017)01-0043-07
10.3969/j.issn.1000-1093.2017.01.006
