火炮弹药协调器区间不确定参数辨识
2017-02-20赵抢抢侯保林
赵抢抢,侯保林
(南京理工大学 机械工程学院, 江苏 南京 210094)
火炮弹药协调器区间不确定参数辨识
赵抢抢,侯保林
(南京理工大学 机械工程学院, 江苏 南京 210094)
火炮弹药协调器是一个复杂的多参数机电液一体化系统,在建立其动力学模型时,某些对系统性能有重要影响的不可测或难以测量的参数,只能通过辨识的方法获得。为了实现弹药协调器的参数辨识,在Simulink中建立弹药协调器的动力学模型与控制模型,并利用区间数描述系统动作过程中的不确定参数;利用区间序关系转换模型,将存在区间不确定参数的辨识问题转换成确定性优化问题进行求解;以协调器支臂角速度曲线的相似度作为优化目标,利用差分进化算法实现了弹药协调器的参数辨识;利用仿真数据确定了此方法的辨识精度满足要求,并利用测试数据对真实系统的参数进行了辨识,验证了此方法的可行性和有效性。
兵器科学与技术;火炮;弹药协调器;参数辨识;区间优化;相似度分析;差分进化算法
0 引言
弹药协调器是大口径自行火炮弹药自动装填系统的一个重要部件,主要用于接收弹仓内被推弹器推送出来的弹丸,再将该弹丸传输到输弹线上,由输弹机输弹入膛[1]。其在武器装备服役使用过程中,时常发生定位精度超差的情况,严重降低了整个弹药自动装填系统的可靠性,亟待进行改进设计。建立其准确的动力学模型,对于推断协调器在运行过程中系统特性的变化情况,进而根据系统特性的变化情况提出改进设计建议,乃至实现故障诊断和预测,都具有重要的意义。
建模过程中的一个核心问题是系统参数的确定,协调器作为一个复杂且多参数的机、电、液一体化系统,其中某些参数是已知的,可通过计算或测试获得;某些是未知且难以测量的,但在系统某次确定的动作循环中,由于动作时间短,可近似认为是确定的,可通过辨识的方法获得;然而,还有一类不确定参数,其真实值即使是在某次确定的动作循环过程中也是变化的,当前的认知手段无法确定其明确的分布规律,但可以确定其变化的区间范围,其他不确定数学方法用来描述这类参数时都存在或多或少的不足,而区间数则可以很好的描述这类参数的不确定性[2]。
根据Ljung[3]的定义,辨识由数据、模型类和准则3个要素组成。其中数据是辨识的基础,准则是辨识的依据,模型类是辨识的范围,辨识就是按照一个准则在一组模型类中选择一个对数据拟合得最好的模型。因此辨识问题可看作是一个优化问题,利用寻优的方法求解。在传统的确定性优化方法中,决策的判断都是基于目标函数和约束在各个设计向量处的具体数值,然而,当用区间数描述系统的不确定参数时,对于任一待辨识的参数,由于不确定参数为一区间数,因此目标函数的可能取值都构成一个区间,无法通过传统的确定性优化方法求解[4]。针对这类存在参数区间不确定的优化问题,一般是通过合适的方法将其转化为确定性问题进行求解。程志强等[5]根据过程工业系统的特点,将区间多目标优化问题转化为一个极大极小问题,并结合遗传算法和非线性规划方法,分析了上述转化的可行性;蒋峥等[6]针对区间单目标非线性优化问题,引入决策风险因子和偏差惩罚项,将区间非线性规划问题转化成一个确定型极大极小问题,并采用遗传算法以递阶优化的方式求解;Jiang等[7]采用区间分析方法计算目标函数的区间值,将上述问题转化为确定性多目标优化问题进行求解。总体来说,现在对于区间不确定问题的研究主要集中在如何将其转换为确定性问题进行求解,而对于其工程应用的研究还较少。
本文为解决存在区间不确定参数的火炮弹药协调器的参数辨识问题,根据协调器的结构和控制原理,在Simulink中建立了协调器的动力学模型和仿真模型;利用区间序关系转换模型,将区间不确定性问题转换为确定性问题进行求解;考虑到协调器的可测响应量为支臂的角速度,将测试曲线与辨识曲线的相似度作为差分进化算法的适应度函数,即优化目标函数,利用差分进化算法对协调器的参数进行辨识。
1 弹药协调器建模
1.1 协调器的动力学建模
弹药协调器的结构如图1(a)所示,由两个并联的串励电机驱动,减速箱由两级直齿轮传动和一级蜗轮蜗杆传动组成,其中蜗轮与火炮耳轴固联;小平衡机由平衡油缸和蓄能器组成,用于平衡弹药协调器的重力矩,减小驱动电机的负载,支撑协调器平稳运动;弹药协调器设置有角位移传感器和角速度传感器(测速度电机),用于提供协调器相对于起落部分的角度信号,使协调器转至正确位置[1]。
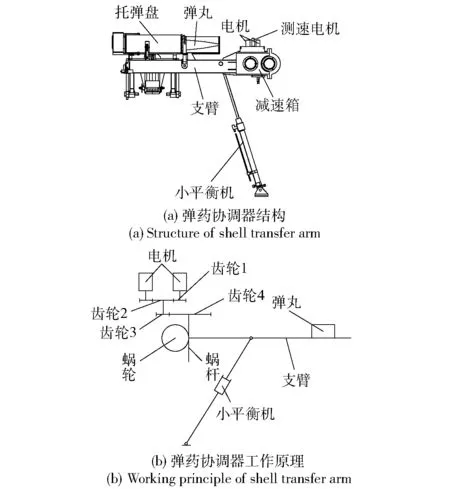
图1 弹药协调器结构及工作原理Fig.1 Structure and working principle of shell transfer arm
弹药协调器的工作原理如图1(b)所示,它是一个单自由度系统,通过进行受力分析,可得到其动力学方程为
(1)
式中:θ为协调器的转角;i1为系统总的传动比;i2为齿轮3到蜗轮的传动比;i3为蜗杆到蜗轮的传动比;η1为齿轮1、2之间的传动效率;η2为齿轮3、4之间的传动效率;η3为蜗轮蜗杆的传动效率;I01为电机和齿轮1的等效转动惯量;I23为齿轮2、3的等效转动惯量;I45为齿轮4和蜗杆的等效转动惯量;I6为蜗轮、支臂和弹丸的等效转动惯量;Td为电机的驱动力矩;TR为小平衡机对支臂的支反力矩;TG为支臂的重力矩。
TG取决于支臂的转角,
TG=Lmgcos(θ+α),
(2)
式中:L为支臂质心到协调器旋转中心的距离;m为支臂和弹丸的质量;α为支臂处于水平位置时,支臂质心到旋转中心连线与水平线之间的夹角。
TR取决于油缸的压力和支臂的转角,其中油缸压力为
p=p0S[V0/(V0-ΔV)]n,
(3)
式中:p0、S为蓄能器的初压和油缸活塞面积;V0为气体初始容积;ΔV为气体变化的体积;n为气体的多变指数。
则平衡机对协调器的作用力矩为
TR=lp0S[V0/(V0-ΔLS)]n,
(4)
式中:l为协调器旋转中心至小平衡机的距离;ΔL为活塞运动的距离。
1.2 电机及控制系统建模
弹药协调器由两个并联的串励电机驱动,相关的动态方程[8]为
(5)
式中:U为电机电压;E为反电动势;R为电机电阻;I为电枢电流;L为电感;Φ为主磁通量;K为励磁系数;Ce、CT分别为反电动势系数和电磁转矩系数;ω为电机转速;T为电机输出转矩。
弹药协调器的控制系统只对达到稳态值所需的时间和定位精度有要求,而对系统的暂态特性没有要求,因此在实际设计系统时需兼顾的各种参数较少,其运动过程可简化为如图2所示的示意图。图2中,A1A2为协调器的运动范围,协调器按要求从A3点运动到A4点,则整个运动过程可分为两段:在A3A5段,只需控制电机的运动方向,给电机加额定电压,使电机全速运动带动协调器快速向A4点运动;当协调器运动到A5点,系统变成一个完全的闭环位置系统,把协调器准确定位在A4点,其速度曲线如图3所示。

图2 协调器运动及定位过程示意图Fig.2 Schematic diagram of motion and location procedure of shell transfer arm
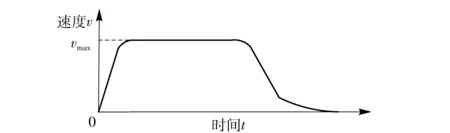
图3 协调器动作过程的速度曲线Fig.3 Angular velocity curve of shell transfer arm
电机的速度是通过驱动电路改变电机电枢上的电压平均值来控制的,电压为准脉冲形式,在功能上类似于脉宽调制。为了实现电机的正转与反转,电机含有两个方向相反的励磁绕组。为了简化驱动电路,功率元件采用绝缘栅双极型晶体管(IGBT)。控制信号由比例- 微分闭环控制产生,当控制信号为正时,与正向励磁绕组连接的IGBT导通;当控制信号为负时,与反向励磁绕组连接的IGBT导通。同时,在触发电路中设置了门限电路,使得IGBT的导通具有迟滞性,以防止两个励磁绕组同时接通。
根据上述分析,在Simulink中建立的协调器的动力学模型与控制模型如图4所示。

图4 弹药协调器的动力学模型与控制模型Fig.4 Dynamic and control models of shell transfer arm
1.3 弹药协调器参数分类
由1.2节建模过程可知,弹药协调器模型包含的参数众多。在一次动作过程中,其中某些参数是可通过计算或测量的方式获得的,如等效转动惯量I01、I23、I45、I6;某些参数是不确定的,无法得知其确定的值,也无法确定其准确的分布规律,只能确定其变化的区间。对于弹药协调器而言,两个区间不确定的参数分别为:
1)蜗轮蜗杆的传动效率η3. 蜗轮蜗杆的传动效率η3=ηnηsηz,其中ηs为考虑搅油损耗时的效率,取值范围0.94~0.99,ηz为轴承效率,滚动轴承取值范围0.98~0.99;ηn为啮合效率,蜗杆为驱动元件时,ηn=tanγ/tan (γ+ρv),其中γ为导程角,ρv为当量摩擦角。ρv与齿面的相对滑动速度有关,而蜗轮蜗杆的相对滑动速度是随协调器的转速变化的。
2)蜗轮蜗杆的传动比i3. 由于传动系统间隙及机械构件受载变形等因素的影响,齿轮及蜗轮蜗杆传动存在空回现象。由1.1节的建模过程可知,系统总的传动比i1,齿轮3到蜗轮的传动比i2都与蜗轮蜗杆的传动比i3有关,因此本文在处理传动空回问题时,将空回对整个传动系统的影响等效在蜗轮蜗杆的传动比i3上。空回非线性迟滞模型为[9]
(6)
式中:B为空回量;θm为驱动端转角;θn为从动端转角;t-、t+分别表示控制过程发生的前后时刻。由(6)式可知,传动比与空回量B相关,而通常情况下空回量B是不确定的。
还有一类参数是未知的,且难以通过测量的方式获得,但这些参数在一次动作过程中可近似地看做确定的,可通过辨识的方法获得的。协调器模型中,3个待辨识参数为:
1)蓄能器的初始压力p0. 小平衡机是通过气囊式蓄能器提供动力的,蓄能器压力的变化直接影响到油缸压力的变化,从而导致协调器运行的不稳定。
2)测速电机的灵敏度k. 测速电机的灵敏度直接影响协调器的定位精度,但火炮射击时的振动、温度的变化、电磁干扰等都将导致灵敏度的异常。
3)气体的多变指数n. 蓄能器在充压过程中,气体的多变指数是个不确定的数值,在其他参数都相同的情况下,多变指数不同,会使蓄能器的储油量发生明显的变化。
2 协调器参数辨识问题描述及其求解方法
本文的弹药协调器参数辨识问题可作为一个优化问题来求解,即:在η3和i3在区间范围内变化的情况下,寻找出最优的p0、k和n,使得模型的输出与真实系统的输出最接近。其数学模型为
(7)
式中:X为设计向量,X=(p0,k,n);D为不确定向量,D=(η3,i3);f为目标函数,是通过辨识获得的协调器角速度曲线与测试所得角速度曲线的相似度;上标I、L和R分别表示区间、区间下界和区间上界。
对于任一确定的设计向量X,由于D的取值范围为一区间量,因此目标函数f(X,D)可能取值也构成一个区间。而在传统的确定性优化方法中,决策的判断都是基于目标函数和约束在各个设计向量处的具体数值,因此,上述问题无法通过传统的确定性优化方法进行求解。为此,本文利用区间序关系将不确定目标函数转换成确定性问题进行求解。
2.1 基于区间序关系的不确定目标函数转换
根据区间数理论[2],区间数被定义为一对有序的实数:
AI=[AL,AR]={x|AL≤x≤AR,x∈R},
(8)
式中:AI、AL、AR分别表示区间、区间下界和区间上界。区间数也可以通过中点Ac和半径Aw来定义为
AI=〈Ac,Aw〉={Ac-Aw≤x≤Ac+Aw,x∈R},
(9)
式中:Ac=(AL+AR)/2,Aw=(AR-AL)/2.
AI≤LcBI,AL≤BL且Ac≤Bc.
(10)
基于(10)式表述的区间序关系≤Lc,可以通过目标函数区间的中点和下界来判断不同设计向量之间的优劣:若设计向量X2优于X1,则X2处的目标函数区间优于X1处的目标函数区间,即fL(X2)≥fL(X1)且fc(X2)≥fc(X1)。因此,希望找到一个最优的设计向量,使得不确定目标函数的区间具有最大的中点值和下界,则(7)式中的不确定目标函数可转换为如下的确定性多目标优化问题:
(11)
式中:对于任一X,需基于不确定目标函数的区间计算其下边界与中点值。此处可通过两次优化过程求解不确定目标函数的区间[10]:
(12)
根据上述转换关系,(7)式表示的不确定优化问题可转换为如下的确定性优化问题:
(13)
为了方便后续算法对其进行求解,此处采用线性加权法将(13)式转换为一单目标优化问题[11]:
(14)
式中:fd为多目标评价函数;β的取值范围为[0,1],为多目标权重,本文中β=0.5;ξ为保证fL(X)+ξ和fc(X)+ξ非负的参数,由于相似度本身为非负数,因此此处ξ=0;φ和ψ为多目标函数的正则化因子,可通过如下优化过程获得
(15)
2.2 时间序列曲线相似度计算
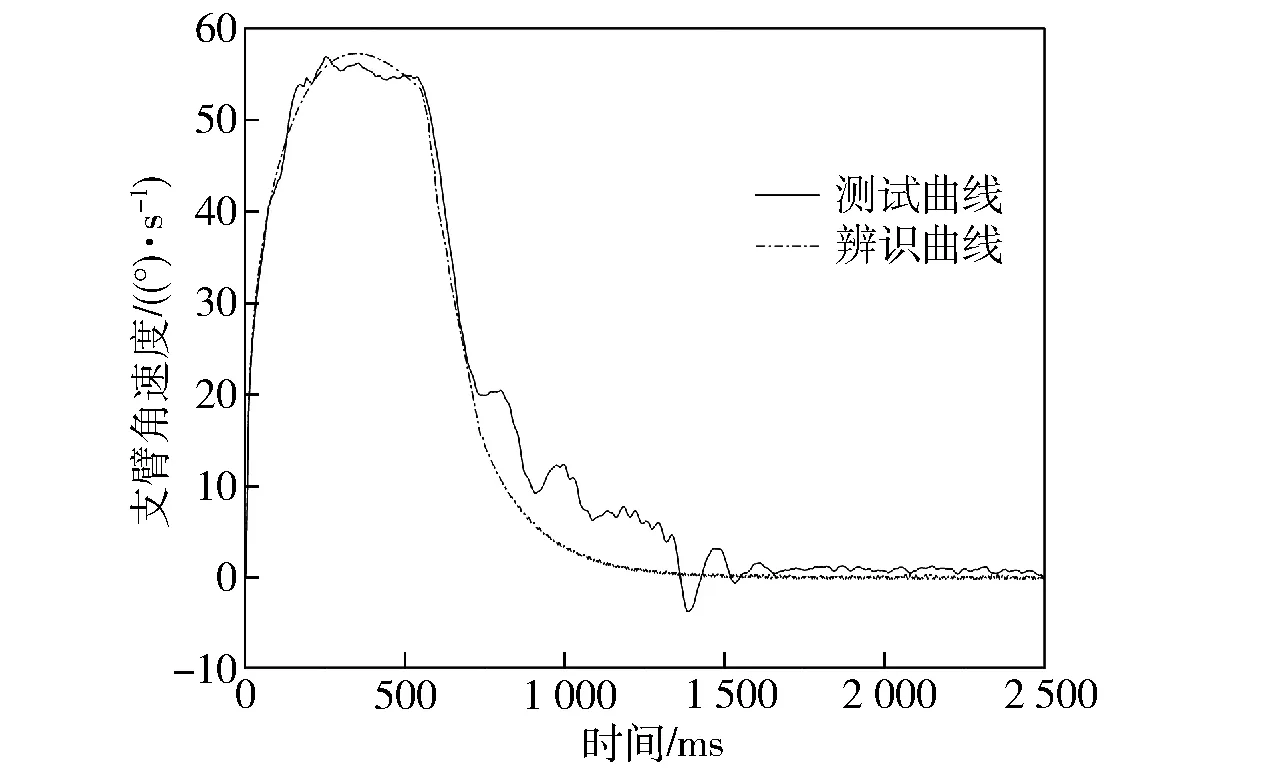
(7)式中,目标函数为通过辨识获得的协调器角速度曲线与测试所得角速度曲线的相似度S,相似度S的范围为[0 1]。S=0表示两个系统一切特性都不同;S=1表示两个系统一切特性均相同;0 对于两个时间序列数值曲线Y=[y1,y2,…,yn]和Y′=[y′1,y′2,…,y′n],其相似度S由数值相似度Sns与形状相似度Sss组成。根据多属性多指标综合理论[13],组合相似度用乘法关系求取比用加法关系求取更合理,则相似度S可表示为 基于区块链的新型IoT技术还处在“萌芽”阶段,对学术界与工业界来说既是机遇又是挑战。区块链与IoT两种技术的融合势必会推动IoT安全的迅猛发展,并由此带来技术的巨大升级。研究适合IoT特征的区块链安全防护技术是未来的一种趋势,但也存在各种挑战而任重道远。 (16) 数值相似度Sns利用相对误差的加权平均值来表示: (17) 式中:si为各点的相似度, (18) δi为任意点的权重,用该点幅值占所有采样点幅值和的比值表示为 (19) (20) (21) 式中:L(·)表示时间序列的长度;m为相似子序列的个数。 计算出Sns和Sss之后,即可根据(16)式计算得到两时间序列曲线的组合相似度S. 2.3 差分进化算法 差分进化算法(DE)是一种模拟自然界生物种群以“优胜劣汰,适者生存”的随机启发式搜索算法,是一种新兴的进化计算技术。DE具有待定参数少,不易陷入局部最优解,以及收敛速度快等特点。DE是基于实数编码的进化算法,由变异、交叉和选择3个基本操作构成,其主要步骤[15]如下: 1)生成初始种群。在N维空间里根据(22)式随机产生满足约束条件的M个个体: (22) 2)变异操作。对于每个目标向量xij,DE根据(23)式进行变异: hij(t+1)=xp1j(t)+F(xp2j(t)-xp3j(t)), (23) 式中:xp1、xp2和xp3为从群体中随机选取的个体,i≠p1≠p2≠p3;F为变异因子,一般可选F为0.3~0.6. 3)交叉操作。为增加群体的多样性,需进行交叉操作,具体操作如下: (24) 式中:CR⊂[0,1],为交叉概率。 4)选择操作。为了确定xi(t)是否为下一代的成员,对于最大化问题,DE对实验向量vi(t+1)与目标向量xi(t)的适应度函数进行比较,并根据(25)式进行选择: (25) 式中:f为相应的适应度函数,本文中f为时间序列曲线的相似度S. 3.1 弹药协调器角速度测试 在进行辨识之前,需对协调器的角速度进行测试,本文利用CS-ARS-02单轴陀螺仪对其进行测试。CS-ARS-02的量程为±200°/s,输出电压为[0 5] V,分辨率≤0.15 °/s,采样频率1 000 Hz. 多次测量的结果如图5(b)所示,从图5(b)中可以看出,测试的结果保持了很好的一致性,证明测试结果是可靠的。此处需要说明的是,在协调器定位阶段,即700 ms之后,协调器的角速度曲线存在明显的振荡,这是由于弹丸在托弹盘中的振动导致的,而仿真模型中弹丸是不存在振动的,因此,在计算曲线相似度时,只取前700 ms的数据,而忽略了700 ms之后的数据。 图5 测试过程与结果Fig.5 Test procedure and results 3.2 弹药协调器的参数辨识 本文利用DE算法实现弹药协调器的参数辨识,辨识过程如下: 1)设置DE算法的参数,在合理范围内初始化种群,利用拉丁超立方采样法,在i3和η3的区间内进行采样,产生不确定参数i3和η3; 2)调用Simulink程序,对于种群中每个个体,结合i3和η3的采样结果进行仿真,获得协调器的角速度曲线族; 3)计算仿真所得角速度曲线与目标角速度曲线的相似度,得到相似度的区间范围,根据(14)式计算得到fd,即DE算法的适应度函数; 4)根据(22)式~(25)式对种群个体进行交叉、变异和选择操作; 5)重复步骤2~步骤4,直到达到最大迭代步数或预设的精度要求,输出最终的最优解,即为辨识结果。 DE参数设置如下:种群个数30,变异因子F=0.7,交叉因子CR=0.6,最大迭代次数G=50. 待辨识参数搜索范围为:蓄能器初压p0[2.8 MPa,3.5 MPa],测速电机灵敏度k[0.6,1.1],气体多变指数n[1.2,2.0]。不确定参数η3和i3的范围分别为[0.47,0.6]和[59,61],拉丁超立方采样个数50. 由于待辨识的参数是不可测或难以测量的,本文利用仿真实验来确定此方法的辨识精度,利用测试数据对弹药协调器的参数进行辨识,以验证此方法的可行性。 表1给出了相应的辨识结果。其中,3组仿真数据中,DE算法对3个待辨识参数辨识结果的平均相对误差分别为0.810 8%、1.487 0%及0.891 8%,可见辨结果的精度较高,满足实际需求;对于图5(b)中的4组测试数据,3个待辨识参数辨识结果的均值分别为3.025 2 MPa、0.997 2及1.498 7,均方差分别为0.010 0 MPa、0.006 9及0.010 2. 其均方差较小,表明辨识结果保持了较好的一致性,且3个待辨识的参数皆与理论值相符。图6是将测试数据的辨识结果平均值代入Simulink模型中计算得出的支臂角速度与测试数据的对比,从图6中可以看出,两者的相似度较高,表明辨识结果是合理的。 表1 辨识结果Tab.1 Identified results 图6 测试结果与辨识结果对比Fig.6 Comparison of test data and identified data 弹药协调器是一个复杂的机电液一体化系统,某些参数往往不能明确地给出其具体数值或分布规律,而只能给出其区间范围。针对利用区间数来描述参数不确定的情况,本文研究了基于DE算法和时序曲线相似度分析的参数辨识方法,获得了以下结论: 1)建立了弹药传输机械的动力学模型和控制模型,并在Simulink中进行求解。 2)利用区间序关系转换模型,将具有参数区间不确定的辨识问题转化成确定性优化问题进行求解。将时序曲线的相似度作为优化目标,利用DE算法实现了存在区间不确定参数的弹药协调器参数辨识。 3)由于待辨识的参数是不可测或难以测量的,本文利用仿真实验确定了此方法的辨识精度满足要求。同时,利用测试数据对弹药协调器的参数进行辨识,验证了此方法是可行性。 References) [1] 侯保林, 樵军谋, 刘琮敏. 火炮自动装填[M]. 北京: 兵器工业出版社, 2010. HOU Bao-lin, QIAO Jun-mou, LIU Cong-min. Ammunition automatic loading system of howitzer[M]. Beijing: Publishing House of Ordnance Industry, 2010. (in Chinese) [2] Alefeld G, Herzberger J. Introduction to interval computations[M]. N Y: Academic Press, INC, 1983. [3] Ljung L. System Identification[M]. Boston: Spring, 1998. [4] 姜潮. 基于区间的不确定性优化理论与算法[D]. 长沙:湖南大学, 2008. JIANG Chao. Uncertainty optimization theory and algorithm based on interval number[D]. Changsha: Hunan University, 2008. (in Chinese) [5] 程志强, 戴连奎, 孙优贤. 区间参数不确定系统优化的可行性分析[J]. 自动化学报, 2004, 30(3): 455-459. CHENG Zhi-qiang, DAI Lian-kui, SUN You-xian. Feasibility analysis for optimization of uncertain systems with interval parameters[J]. Acta Aytomatica Sinica, 2004, 30(3): 455-459. (in Chinese) [6] 蒋峥, 戴连奎, 吴铁军. 区间非线性规划问题的确定化描述及其递阶求解[J]. 系统工程理论与实践, 2005, 25(1): 110-116. JIANG Zhen, DAI Lian-kui, WU Tie-jun. Deterministic interpretation of interval nonlinear programming and its hierarchical optimization solution[J]. Systems Engineering-Theory & Practice, 2005, 25(1): 110-116. (in Chinese) [7] Jiang C, Han X, Guan F J, et al. An uncertain structural optimization method based on nonlinear interval number programming and interval analysis method[J]. Engineering Structures, 2007, 29(11): 3168-3177. [8] 李红伟. 串励电机特性模拟与分析[J]. 微电机, 2010, 43(8): 95-97. LI Hong-wei. Characteristic simulation and analysis of series motor[J]. Micromotors, 2010, 43(8): 95-97. (in Chinese) [9] Su C Y, Stepanenko Y, Svoboda J, et al. Robust adaptive control of a class of nonlinear systems with unknown backlash-like hysteresis[J]. IEEE Transactions on Automatic Control, 2000, 45(12): 2427-2432. [10] 马龙华. 不确定系统的鲁棒优化方法及应用研究[D].杭州: 浙江大学, 2002. MA Long-hua. Research on method and application of robust optimization for uncertainty system[D]. Hangzhou: Zhejiang University, 2002. (in Chinese) [11] 孙晓辉, 丁晓红. 结构多目标拓扑优化设计[J]. 机械设计与研究, 2012, 28(4): 1-4,9. SUN Xiao-hui, DING Xiao-hong. Research on multi-objective topology optimization design methods for structure[J]. Machine Design and Research, 2012, 28(4): 1-4, 9. (in Chinese) [12] 何江. 基于混合动态仿真的发电机模型有效性评估及参数校正研究[D]. 重庆: 重庆大学, 2011. HE Jiang. Research on validity evaluation and parameter calibration of generator model based on hybrid dynamic simulation[D]. Chongqing: Chongqing University, 2011. (in Chinese) [13] Xu Z H. Uncertain multi-attribute decision making: methods and applications[M]. Heidelberg : Springer, 2015. [14] 杨玉良, 秦俊奇, 狄长春, 等. 火炮动力后坐实验台建模及射击模拟准确度评估[J]. 振动与冲击, 2014, 33(10): 127-130. YANG Yu-liang, QIN Jun-qi, DI Chang-chun, et al. Modeling and firing simulation accuracy assessment of a gun-power-recoil test table[J]. Journal of Vibration and Shock, 2014, 33(10): 127-130. (in Chinese) [15] Price K, Storn R M, Lampinen J A. Differential evolution: a practical approach to global optimization[M]. Heidelberg: Springer, 2006. Identification of Interval Uncertainty Parameters of a Howitzer Shell Transfer Arm ZHAO Qiang-qiang, HOU Bao-lin (School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China) Shell transfer arm is a complicated mechatronic and hydraulic integrated system of howitzer with multi-parameters. During the modeling process, some parameters are hard or unable to be measured but have significant effect on the performance of shell transfer arm, which can only be achieved by identification. For identifying the parameters of shell transfer arm, the dynamic and control models are built in Simulink, and the uncertainty parameters are described by interval number. The identification problem of interval uncertainty parameters is transformed into a certainty optimization problem via order relation of interval number transformation model. The similarity of angular velocity of shell transfer arm is set as the optimization objective function, and three parameters are identified by differential evolution (DE) method. The proposed method is verified by simulated and test data. The identification results of simulated data show that the identification accuracy satisfies the requirement, and the identification results of test data show that the proposed method is feasible and effective. ordnance science and technology; howitzer; shell transfer arm; parameter identification; interval optimization; similarity analysis; differential evolution method 2016-06-28 国家“973”计划项目(6132490102); 国家自然科学基金项目(51175266) 赵抢抢(1987—), 男, 博士研究生。 E-mail: zqqlzl@139.com 侯保林(1965—), 男, 教授, 博士生导师。 E-mail: houbl@njust.edu.cn TJ303+.3 A 1000-1093(2017)01-0035-08 10.3969/j.issn.1000-1093.2017.01.005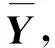
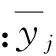

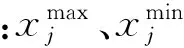
3 系统测试与参数辨识

4 结论
