仿鱼体柔性变形运动流噪声特性研究

王亚东，杨晓光，张纪华

(北京机电工程研究所，北京 100074)

仿鱼体柔性变形运动流噪声特性研究

王亚东，杨晓光，张纪华

(北京机电工程研究所，北京 100074)

鱼类游动具有低噪声、高效率等特点，鱼体摆动可抽象并表征为壁面的柔性变形运动。柔性变形将诱导产生复杂的涡系流场结构，其流噪声的形成机理及特性在很大程度上有别于常规问题。以美国国家航空咨询委员会开发的NACA0012翼型为研究对象，考虑流噪声计算的需求，建立可模拟柔性变形的数值模型。基于声类比理论获得其流噪声特性，揭示柔性变形对流噪声的影响机制，获得流噪声辐射场指向性。结果表明：柔性变形运动诱发的复杂涡系流场演变是流噪声的主要来源；不同方位下流噪声总声压级随距离的增加均呈衰减趋势；在柔性变形壁面正上方和正下方，辐射噪声达到极值，噪声指向与偶极子声源的辐射场特性最为相似。

声学；柔性变形；声类比法；流噪声

0 引言

水下鱼类游动具有低噪声、高机动和高推进效率等优势，逐渐成为了仿生设计的重要对象之一。鱼类游动过程的推进方式分为尾鳍摆动推进(BCF)和胸鳍波动推进(MPF)两种，其中尾鳍摆动推进是大多数鱼类游动的主要方式。

国内外学者目前针对尾鳍摆动模式推进的鱼类游动流场复杂涡系结构、推力产生机理进行了大量的研究。Borazjani等[1]建立了壁面柔性变形的数值模拟方法，利用其系统研究了雷诺数Re、摆动频率、斯特劳哈尔数St对尾鳍摆动推进鱼类游动的影响，提出了尾鳍摆动过程引起的单列涡和双列涡推进模式，揭示了其流场结构。苏玉民等[2]设计了一套仿鱼尾鳍推进系统试验模型，针对摆动尾鳍产生的水动力进行了试验研究，探讨了不同尾鳍形状对推进效率、推力和侧向力系数的影响。随着研究的不断深入，开始涉及用试验手段探索推进水动力产生机理[3]，研究结构物与鱼群之间的相互作用[4]、多尾鳍推进[5]及鱼群间不同个体的相互影响机制[6]等。

随着理论的发展和计算能力的不断提高，采用数值计算方法来进行流噪声的分析和设计已成为一项重要工作。曾赛等[7]利用计算流体力学(CFD)方法分析了对转桨非空化线谱噪声的产生机理，得到的对转桨非空化线谱频率以及声压方向性与理论结果吻合较好。石磊等[8]同样应用大涡模拟方法和Ffowcs Williams & Hawkings(FW-H)方程分析了美国国家航空咨询委员会开发的NACA0018翼型气动噪声，在翼型前缘和后缘仿照鸟类的锯齿状羽毛分布，设计几种不同的仿生模型，取得了良好的降噪效果。诸多研究均证明了数值方法在流噪声问题研究中已具备一定的可行性。

从检索到的文献看，目前的研究多集中于尾鳍摆动流场结构、宏观受力等内容，关于鱼体柔性摆动过程流噪声特性的研究还较罕见。鱼体摆动过程是壁面柔性非定常变形过程，其引起了复杂的涡系结构生成、演变，必将诱发有异于常规绕流的流噪声特性，而噪声特性是开展仿生设计的重要内容之一。

本文以NACA0012翼型为研究对象，以指定的运动规律赋予其柔性变形，基于动网格方法、声类比理论建立了非定常数值分析模型，通过压力分布及涡系流场结构等证明了流场求解方法的有效性，对比分析了湍流模型对结果的影响，获得了壁面柔性变形诱发的流噪声特性，揭示了不同频段内的声压级分布及辐射噪声指向特性。

1 数值计算方法

1.1 摆动规律

采用NACA0012标准翼型为计算对象，翼型弦长为300 mm. 在计算过程中，整个翼型表面满足柔性变形，其变形按照文献[9]中提出的运动模型形式来给定。在翼型对应的坐标系下，翼型中线的摆动规律为

y(x,t)=a(x)sin (kx-ωt+φ0),

(1)

式中：a(x)=c3x3+c2x2+c1x+c0为振幅；k=2π/λ为波数，λ为周期摆动时的波长；ω=2π/T为圆频率，T为摆动周期；φ0为初始相位。

在整个柔性变形过程中，采用数值求解、控制来保证翼面中轴线总长度不变。在本文中，(1)式中参数取值为c2=c1=c0=0,c3=0.3/l2,l=0.3 m,ω=2π,k=0.

计算中来流速度v为1.2 m/s，根据摆动周期T=1 s和特征长度l=0.3 m，可计算出斯特劳哈尔数st=l/vT=0.25.

1.2 网格与模型

采用如上的模型参数来控制壁面柔性变形，以动网格来适应边界变形。全场采用非结构网格来建立，计算域尺寸为6.0 m×3.0 m，如图1所示。为了满足大涡模拟的需求，近壁面首层网格按照y+≈5来建立，翼型表面共布置900个点，网格总量为82万。

图1 计算区域与网格示意Fig.1 Schematic diagram of computational domain and mesh

壁面柔性变形过程中，实时重构网格，通过调整重构参数，保证全过程的网格质量，以满足流噪声计算对网格质量的高要求，完整变形周期后的网格如图2所示。

图2 全周期变形后的网格示意Fig.2 Schematic diagram of mesh throughout a time period

1.3 声场求解

利用声类比方法求解壁面柔性变形诱发流噪声特性的流程为：利用大涡模拟计算获得非定常湍流流场，提取柔性壁面附近声源的强度及分布特性，再利用FW-H方程积分外推求解出其诱发的声场。

FW-H方程可联合连续方程和Navier-Stokes方程推导得出[10]，其表达式为

(2)

式中：f为源面变量；ui是流体在xi方向的速度分量；un是流体在面f=0上的法向速度；vn为物面速度的法向分量；δ(f)是狄利克雷函数；H(f)是Heaviside广义函数，定义见(3)式；p′是远场的声压，定义见(4)式；Tij是Lighthill应力张量，定义见(5)式，δij为单位张量；Pij为可压流体应力张量，定义见(6)式；a0为远场声速；nj为指向外部区域的单位法向向量在j方向的分量；ρ为流体密度；对于未受扰动的量，用下标0表示。

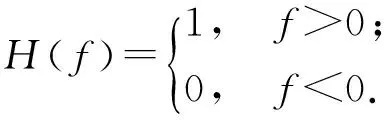
(3)

p′=p-p0，

(4)

(5)

(6)

p、p0分别为流体受扰动和未受扰动的压力，μ为流体的黏性系数。

利用自由空间的格林函数解，可求得FW-H方程积分形式的解，具体过程可参考文献[10]。

在本文计算过程中，首先以1×10-3s的时间步长计算6个摆动周期，再变更时间步长为1×10-4s计算4个摆动周期，启动声学计算模块后取10个摆动周期作处理分析。

1.4 监测点布置

为了了解柔性壁面变形过程的声辐射场特性，设置20个声监测点，如图3所示。

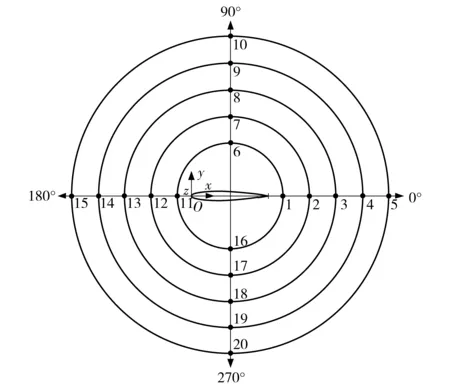
图3 噪声监测点布置Fig.3 Layout of acoustic monitors

如图3所示，监测点位于5个同心圆的4个不同方位上，首个圆的半径为200 mm，相邻同心圆间隔为50 mm.

2 结果与分析

2.1 数值方法验证

可公开检索到的文献中，针对壁面柔性变形诱发的流噪声测量试验较为罕见，缺乏直接对比的数据。根据本文数值方法建立的思路，流场计算结果作为输入，利用声类比理论进行噪声分析，而声类比方法在流噪声领域已经得到了广泛的运用和验证，故数值方法验证的核心问题是流场的校验。

本文所采用的流噪声计算方法，其计算精度主要取决于流场计算所得的压力脉动模拟精度。为了验证所采用的网格和数值方法的可行性，暂不考虑翼面的柔性变形，选用大涡模拟(LES)模型的数值方法开展仿真，利用文献[11]针对NACA0012翼型开展的Re=2.88×106状态下风洞试验数据，对比0°攻角和10°攻角下吸力面的压力分布，如图4所示。

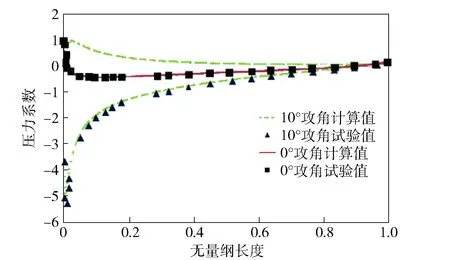
图4 NACA0012翼型压力分布特性对比Fig.4 Comparison of pressure distribution characteristics of NACA0012

从对比结果可以看出，本文所建立的数值方法在模拟绕流流动时所获得的压力分布数据与试验结果吻合程度较好。

为了进一步验证本文所涉及的非定常运动计算的可信度，利用文献[12]在水洞中开展的NACA0012翼型扑动状态流场尾迹试验数据，与采用LES模型的数值方法开展计算获得的结果对比如图5所示。图5(a)给出了翼型摆动中间时刻的流场涡量图(空白区域代表超过了设置的显示阀值)，图5(b)为水洞试验实测图像，可见二者的基本特性是一致的。

图5 非定常流场涡街结构Fig.5 Unsteady flow field of vortex structure

上述静态与动态、定量及定性的对比与分析，可在一定程度上证明本文所采用的流场数值计算方法的有效性，保证提供与真实相符的噪声求解输入，为后续的噪声计算与分析奠定基础。

2.2 湍流模型影响

为了确定湍流模型对壁面柔性变形过程流噪声数值模拟结果的影响，分别选用重整化群(RNG)k-ε、剪切压力传输(SST)k-ε、LES、分离涡模拟(DES)湍流模型进行计算。

图6 不同湍流模型对应的阻力系数与时间历程Fig.6 Drag coefficients vs. time of different turbulent models

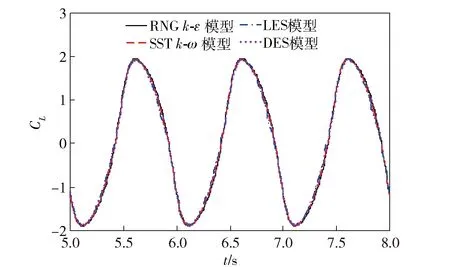
图7 不同湍流模型对应的升力系数与时间历程Fig.7 Lift coefficients vs. time of different turbulent models

从图6和图7中可以看出，湍流模型对壁面柔性变形过程中的宏观受力影响较小。

选定0°方位(1～5号测点)和90°方位(6～10号测点)方位为代表，对比不同湍流模型所对应的总噪声级，结果如图8所示。

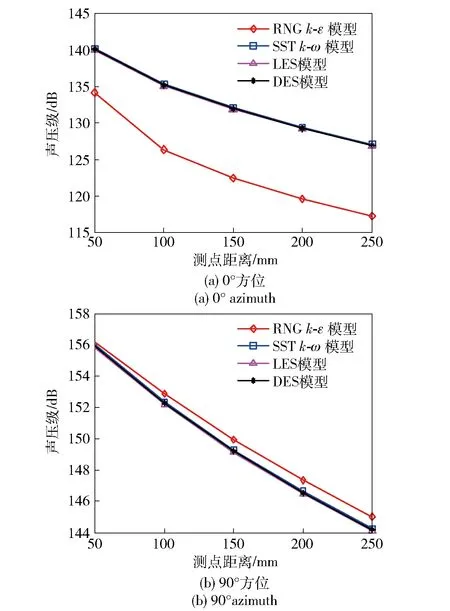
图8 总声压级随距离变化Fig.8 Total sound pressure level (SPL) vs. distance

由计算结果可知：在本文研究的范畴下，选用SSTk-ω、LES、DES湍流模型计算所得的总声压级变化趋势基本一致；RNGk-ε模型在不同方位均存在一定的偏差，可能的原因在于其近壁面流动捕捉能力弱于其他模型，未能精细化求解较小尺度的涡流，进而导致总声压级的差异。

不同湍流模型计算结果的差异在宏观受力上难以体现，而反映至声学相关的压力脉动特征，则存在一定的差异。

2.3 噪声辐射特性

选定0°方位(1号测点)、90°方位(6号测点)、180°方位(11号测点)、270°方位(16号测点)，对比4个不同方位监测点所得频域内的噪声级分布，结果如图9所示。

图9 不同频率的声压级分布Fig.9 SPL distribution in frequency domain

由图9可知，不同方位对应噪声级的频域分布存在一定差异：0°方位声压级在500Hz以内迅速衰减，1 000～2 500Hz略有上升，而后缓慢下降；90°和270°方位，噪声在1 000Hz以内衰减迅速，在1 000～5 000Hz分布较均匀，由于对称性，二者特性基本一致；180°方位在1 000Hz以内的衰减介于0°和90°之间，在1 000～5 000Hz分布亦较均匀。这种噪声分布有可能与柔性变形所导致的多尺度涡生成、脱落与演化有关，可参见图5(a)给出的计算所得流场涡系结构。

将图3所示的20个监测点的数据按照不同方位来组织，得出各方位对应的总噪声级随距离变化的结果如图10所示。

图10 不同方位下的总声压级随距离变化Fig.10 Total SPL in different directions vs. distance

结果表明：不同方位总声压级随距离增加均呈衰减趋势；90°方位和270°方位总噪声级水平在不同距离的分布基本一致，这体现了柔性变形所导致流场的对称性；在同尺度距离上，各方位的总噪声级衰减程度是不同的，180°方位衰减值最大。

2.4 噪声来源分析

保持其他条件相同，设置了不变形的固定NACA0012翼对比工况，计算所得90°方位不同距离所对应的总噪声级，如图11所示。

图11 变形/不变形下的总声压级随距离变化Fig.11 Total SPL vs. distance in deformation and non-deformation cases

增加柔性变形后，总噪声级大为增加，可判定柔性摆动产生的复杂涡系结构是辐射噪声的主要来源。

2.5 噪声指向性

以15°为间隔，距离中心300mm的圆周上布置24个声音监测点，获得其总声压级以分析噪声指向性，结果如图12所示。

图12 不同方位的总声压级Fig.12 Total SPL in different directions

从图12中可以看出：噪声在柔性壁面正前方和正后方较低，且正后方要低于正前方数值；在柔性壁面正上和正下方，辐射噪声达到极值，且随方位变化减弱，呈现为偶极子声源的辐射场特性。

3 结论

基于流体计算软件，考虑计算声学的需求，建立了可模拟壁面柔性变形的数值模型，并采用声类比方法获得了壁面柔性变形过程中的流噪声特性，主要结论如下：

1)壁面柔性变形诱导产生复杂的涡系流场结构，涡的生成、脱落和演化是较高强度流噪声的主要来源。

2)壁面柔性变形诱发的流噪声辐射场具有指向性，翼面0°、180°方位总噪声级最低，翼面90°、270°方位总噪声级达到极值，呈偶极子声源特性。

3)流噪声随距离增加迅速衰减，不同方位的衰减特性不同，翼型180°方位总噪声级衰减最快。

4)仿真的壁面柔性变形并未达到真实生物的低噪声效果，在一定程度上表明生物对涡流的智能控制、柔性材料等方面均对流噪声有较大的影响。

References)

[1] Borazjani I, Sotiropoulos F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes[J]. Journal of Experimental Biology, 2008, 211(10):1541-1558.

[2] 苏玉民, 杨亮, 赵士奇, 等. 仿鱼尾鳍推进系统的水动力性能试验[J]. 华中科技大学学报:自然科学版, 2009, 37(9):82-85.

SU Yu-min, YANG Liang, ZHAO Shi-qi, et al. Experimental study on hydrodynamic performance of a bio tail fin propulsive system[J]. Journal of Huazhong University of Science & Technology:Natural Science Edition, 2009, 37(9):82-85. (in Chinese)

[3] Hannon J W. Image based computational fluid dynamics modeling to simulate fluid flow around a moving fish[D]. Iowa City, IN,US:University of Iowa, 2011.

[4] Frank E F, Paul L, Terrie M W, et al. Measurement of hydrodynamic force generation by swimming dolphins using bubble DPIV[J]. Journal of Experimental Biology, 2014, 217(2):252-260.

[5] 张智伟, 易淼荣, 敬军, 等. 多尾鳍仿生航行器推进性能的三维数值研究[J]. 空气动力学学报, 2014, 32(5):634-640. ZHANG Zhi-wei, YI Miao-rong, JING Jun, et al. Proposion performace of three-dimensinal biomimetic underwater vehicle[J]. Acta Aerodynamica Sinica, 2014, 32(5):634-640. (in Chinese)

[6] 王亮, 王明, 付强, 等. 并列仿生鱼自主游动的数值模拟研究[J]. 计算力学学报, 2014, 31(1):101-109. WANG Liang, WANG Ming, FU Qiang, et al. Numerical simulation of two self-propelled fish swimming in a side-by-side arrangement[J]. Chinese Journal of Computational Mechanics, 2014, 31(1):101-109. (in Chinese)

[7] 曾赛, 杜选民, 范威. 水下对转桨非空化线谱噪声分析与数值研究[J]. 兵工学报, 2015, 36(6):1052-1060. ZENG Sai, DU Xuan-min, FAN Wei. Numerical simulation and analysis of non-cavitation noise line-spectrum frequency of underwater counter-rotation propeller[J]. Acta Armamentarii, 2015, 36(6):1052-1060. (in Chinese)

[8] 石磊, 张成春, 王晶, 等. NACA 0018翼型模型的仿生降噪[J]. 吉林大学学报:工学版, 2011, 41(6):1664-1668. SHI Lei, ZHANG Cheng-chun, WANG Jing, et al. Reduction of aerodynamic noise from NACA0018 airfoil model using bionic methods[J]. Journal of Jilin University:Engineering and Technology Edition, 2011, 41(6):1664-1668. (in Chinese)

[9] Wolfgang M, Anderson J M, Grosenbaugh M A, et al. Near-body flow dynamics in swimming fish[J]. Journal of Experimental Biology, 1999, 202(17):2303-2327.

[10] Lyrintzis A S. Surface integral methods in computational aeroacoustics: from the (CFD) near-field to the (acoustic) far-field[J]. International Journal of Aeroacoustics, 2003, 2(2): 95-128.

[11] Gregory N, O’Reilly C L. Low-speed aerodynamic characteristics of NACA 0012 aerofoil section, including the effects of upper-surface roughness simulation hoar frost, R&M 3726[R]. Washington DC,US:NASA, 1970.

[12] Jones K D, Dohring C M, Platzer M F. Wake structures behind plunging airfoils: a comparison of numerical and experimental results, AIAA 1996-0078[R]. Reston, VA, US:AIAA, 1996.

Research on the Characteristics of Flow Noise Induced by Fish-like Flexible Deformation Motion

WANG Ya-dong, YANG Xiao-guang, ZHANG Ji-hua

(Beijing Electro-mechanical Engineering Institute，Beijing 100074, China)

Fish swimming has the characteristics of low noise, high efficiency, and the swing of fish body can be abstracted as a flexible wall deformation motion. Flexible deformation can induce a complex vortex structure in the flow field, of which the flow noise formation mechanism and characteristics are different from the conventional problems in a large extent. The NACA0012 airfoil developed by National Advisory Committee for Aeronautics is used as the research object. Considering the demand of flow noise calculation, a numerical model based on the acoustic analogy theory is set up to simulate the flexible deformation, revealing the mechanism of the effect of the flexible deformation on noise characteristics, and radiation directivity of flow noise is obtained. The results indicate that the complex vortex structure evolution induced by flexible deformation is the major source of flow noise; the total sound pressure levels at different orientations decrease with the increase in distance; the total sound pressure level tends to be maximum just above and below the flexible deformation wall, and the noise radiation directivity is most similar to the radiation directivity of a dipole source.

acoustics; flexible deformation; acoustic analogy theory; flow noise

2015-08-06

王亚东(1985—)，男，工程师。E-mail:roby868@163.com

O427.5

A

1000-1093(2017)01-0123-06

10.3969/j.issn.1000-1093.2017.01.016