基于相位差分的弹丸进动周期提取

刘志学，宫志华，冷雪冰

(中国白城兵器试验中心, 吉林 白城 137001)

基于相位差分的弹丸进动周期提取

刘志学，宫志华，冷雪冰

(中国白城兵器试验中心, 吉林 白城 137001)

进动周期是表征炮弹、火箭弹等常规武器无控弹丸弹道特性的重要指标。为有效获取弹丸进动周期，提出了基于相位差分的弹丸进动周期提取方法。弹丸进动会对连续波雷达回波产生微多普勒调制，建模分析表明，进动弹丸的微动速度遵循正弦规律变化，其相位变化率与进动周期呈反比关系。利用Hilbert变换可以提取微动速度的瞬时相位，由相位差分即可获得弹丸进动周期。仿真实验验证了该方法对信噪比大于7 dB的微动速度提取进动周期具有更好的性能。利用该方法对实际测量数据进行处理，获取了弹丸准确、平滑的进动周期数据。

兵器科学与技术；连续波雷达；进动周期；微多普勒；Hilbert变换

0 引言

炮弹、火箭弹等常规武器无控弹丸(以下简称弹丸)发射时，扰动因素使弹轴偏离预定速度矢量方向，影响射击精度和飞行稳定。高速自旋运动形成一个使弹丸围绕质心转动的力矩，使弹轴围绕速度矢量方向旋转，弹道学上称之为进动[1]。进动特性同弹丸的弹道特性、电磁散射特性一样, 是弹丸的固有属性, 可以作为弹丸类目标识别的重要特征量，也可以用来验证弹丸的设计以及分析落点散布。

相对于弹丸的飞行来讲，进动属于微动[2-3]，对雷达回波产生幅度和相位调制。其中幅度调制使目标雷达散射截面(RCS)序列呈现周期性变化，基于RCS序列的目标进动周期提取方法研究开展的较早，美国开展的Firefly飞行试验专门研究进动特性[4]，但技术细节未披露。现有关于提取RCS序列周期的方法包括周期图法[5-6]、自相关函数法[7]、平均幅度差函数法[8]、循环幅度差函数法、循环自相关函数法，以及循环幅度差结合自相关函数法[9-10]等，文献[11]利用三角函数来拟合RCS序列，再求得使拟合误差最小的进动频率, 文献[12]对经过平动和微动调制后的弹丸RCS数据进行分析后,利用希尔伯特- 黄变换(HHT)时频分析算法提取出了进动周期。总的来讲，基于RCS序列的目标进动周期提取利用的是弹丸进动对雷达回波的幅度调制信息，但该类方法对雷达回波信噪比、RCS序列循环平稳性和观察时间要求较高。

进动对雷达回波的相位调制产生微多普勒信号，并叠加到多普勒信号上[13]。微多普勒调制信号反映了微动的瞬时相位特性，其频率表征了目标瞬时微动速度。微多普勒目前主要用于弹道导弹、旋翼直升飞机的分析识别，以及人体手、脚的摆动和桥梁的振动等探测，而关于弹道目标微动特性研究的技术文献较少[13-14]。文献[15]研究了基于经验模态分解算法的多分量正弦调频信号分离方法,并使用短时傅里叶变换得到了每个本征模态函数的瞬时频率；文献[16]中提出了利用回波相关方法和频谱展宽估计进动参数的方法；文献[17]利用时域滑窗自相关处理方法提取了弹丸进动周期。上述方法本质上是利用微多普勒信号周期间的相关性来估计周期，短时傅里叶变换对数据量有较高要求，自相关函数类方法的误差较大。

本文着重分析弹丸进动对连续波雷达回波产生的微多普勒调制模型，针对进动微动速度的特点,提出了通过Hilbert变换求取微动速度相位，利用相位差分估计弹丸进动周期的数据处理方法,可以有效提取弹丸进动周期。

1 进动调制模型

连续波雷达在对弹丸采用尾追式跟踪测量时，弹丸进动示意图如图1所示。定义进动坐标系[1]：以弹丸质心为坐标系原点o；以弹丸质心速度方向线为ox轴，沿质心运动方向为正；oy轴垂直于ox轴，向上为正；oz轴按右手法则确定，垂直于oxy平面，向右为正。这样定义的进动坐标系在外弹道学中亦称为弹道坐标系。

图1 进动示意图Fig.1 Schematic diagram of precession

设弹丸自旋角速度为ω，弹轴进动角速度为Ω，进动时弹轴与速度方向ox轴夹角为θ. 雷达发射电磁波照射弹丸，弹上主要散射点P位于弹丸底部，P点与弹丸质心距离为l，则散射点P在弹道坐标系中的坐标如(1)式所示：

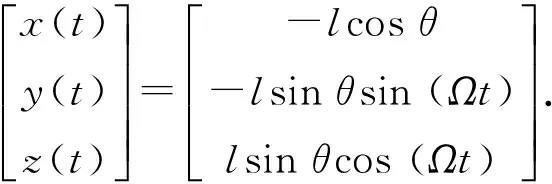
(1)

再建立雷达测量坐标系，如图2所示。OX轴沿水平线平行射击面，射击方向为正；OY轴垂直于OX轴，向上为正；OZ轴按右手法则确定，垂直于OXY平面，向右为正。

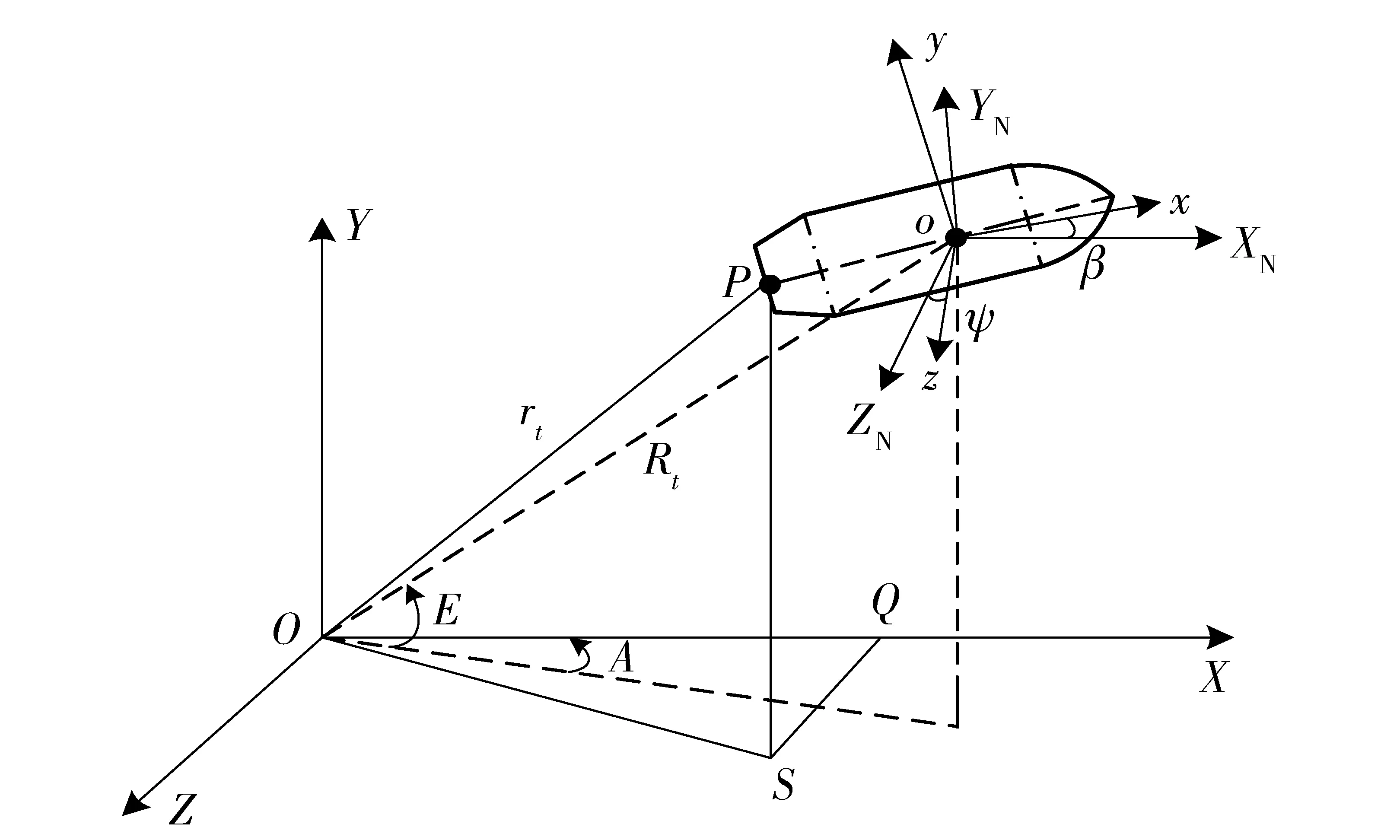
图2 雷达测量坐标系与弹道坐标系几何关系Fig.2 Geometric relationship of radar coordinate system and trajectory coordinate system

将雷达测量坐标系平移至弹丸质心o形成基准坐标系oXNYNZN.ox轴与oXN轴夹角β为速度高低角，oz轴与oZN轴夹角ψ为速度方向角。

弹上主要散射点P在基准坐标系中的坐标值可由弹道坐标系经两次旋转而成，如(2)式所示：

(2)

通常情况下弹丸的速度方向角ψ≈0，由此可得散射点P在任意时刻到雷达的瞬时斜距rt，如(3)式所示：

(3)

式中：a=-lcosθ(cosβcosEcosA+sinβsinE)；b=lsinθcosEsinA；c=lsinθ(sinβcosEcosA-cosβsinE)；Rt为雷达到弹丸质心的斜距；A为雷达测量弹丸方位角；E为雷达测量弹丸俯仰角。

在一定的观察时间内，方位角A和俯仰角E近似为常数，因此(3)式对时间求导数得到弹丸主要散射点的径向速度为

(4)

式中：

vd(t)为弹丸质心的径向速度；vm(t)为弹丸进动引起的微动速度(简称微动速度)；vr(t)为弹丸的径向速度。当目标远离雷达时Rt≫l，这时g≈1,q≈1,则弹丸的径向速度可以化简为

vr(t)≈vd(t)+vm(t),

(5)

而微动速度可以表示为

vm(t)=-bΩsin (Ωt)+cΩcos (Ωt)=
dΩcos (Ωt+φ),

(6)

通过上述分析可知，弹丸的径向速度是质心径向速度与微动速度之和，且微动速度遵循正弦规律变化,其相位与进动周期的关系为

(7)

式中：Ф(t) 为微动速度相位;Tm为进动周期;fm为进动频率。

2 进动周期提取方法

弹丸的进动频率一般很低，直接采用频域处理的方法提取进动频率，其分辨力难以满足要求。采用时域滑窗自相关处理方法提取的进动周期数据率低，受噪声影响较大。从现实物理意义上来说，进动频率与微动速度的相位在时域上存在积分匹配的关系，即通过对微动速度的相位的微分可以得到微动频率。

弹丸的进动周期为非线性变化的，所以微动速度为非平稳信号，其频率和周期的定义方式是以Hilbert变换为基础的。对微动速度进行Hilbert变换,求出解析信号再对其相位微分,可以得到频率，而周期与频率互为倒数。由(6)式可知，微动速度遵循正弦规律变化，具有窄带特性，可以应用Hilbert变换提取瞬时参数。为此本文提出了基于Hilbert变换相位差分的进动周期提取方法，提取流程如图3所示。

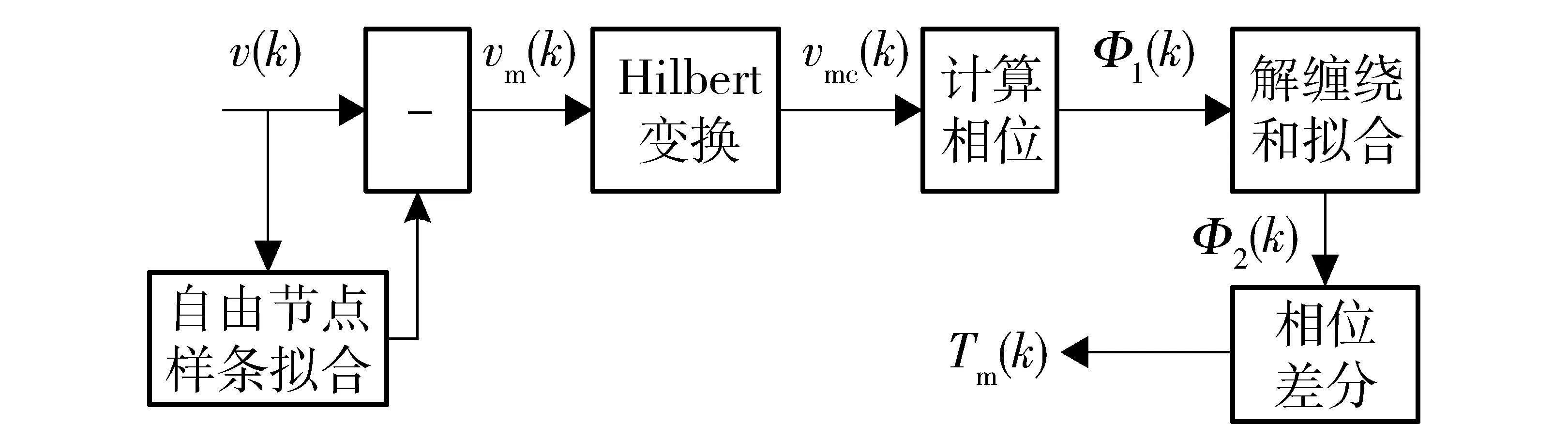
图3 进动周期提取流程Fig.3 Flow chart of precession period extraction

微动速度vm(t)的Hilbert变换为

(8)

式中：vmi(k)为vm(k)的Hilbert变换；τ是卷积中间变量；vmc(k)为vm(k)的复数解析形式，vm(k)是vmc(k)的实部，vmi(k) 是vmc(k)的虚部。vmc(k)的相位为

(9)

由Φ1(k)估计进动周期，需要对其进行数值微分,利用向前差商法可以实现

Tm(k)=2πTs/[Φ1(k+1)-Φ1(k)],

(10)

式中：Ts为径向速度的采样间隔。

从雷达测量数据提取飞行弹丸进动周期，由于弹丸质心的径向速度vr(t)和微动速度vm(t)存在固有的线性耦合现象，对雷达录取的目标径向速度进行自由节点样条函数拟合[18]获得弹丸质心的径向速度，提取微动速度数据vm(t)；对微动速度数据vm(t)进行Hilbert变换获得微动速度的解析形式数据vmc(t)，求取解析微动速度vmc(t)的相位Ф(t)；对Ф(t)进行自由节点样条函数拟合消除测量噪声的影响；利用(10)式求取进动频率和进动周期。

3 仿真及试验分析

连续波雷达测量目标径向速度时不可避免地 引入测量误差，此时雷达输出的弹丸径向速度由(5)式扩展为

vr(t)=vd(t)+vm(t)+n(t),

(11)

式中：n(t)为连续波雷达速度测量误差，服从～[0,σ2]正态分布，σ2为连续波雷达速度测量误差功率。在考核进动周期提取方法的性能时必须考虑速度测量误差的影响，为此(6)式和(11)式可得微动速度功率与速度测量误差功率之比，即微动速度信噪比SNR，

(12)

3.1 仿真实验

为了验证文中提出的进动周期提取方法的性能，作如下仿真：时间t=0～25 s，采样间隔Ts=0.01 s，速度测量误差服从～[0, 0.1]正态分布，质心径向速度vd=(0.4t2-15t+660) m/s，微动速度vm=Amcos(2πt/Tm)，其中，Am为微动速度振幅，进动周期Tm=1/(0.5+0.02t) s. 信噪比SNR从3 dB到14 dB变化，作200次Monte Carlo仿真实验，得到的仿真结果如图4所示。从仿真结果可以看出：当信噪比大于7 dB时，相位差分法的性能优于自相关法；当信噪比小于7 dB时，由于基于Hilbert变换的相位计算对噪声比较敏感，利用相位差分法提取的进动周期会发生错误，进动周期估计误差显著提升，相位差分法不再可用。

图4 相位差分法性能分析Fig.4 Analysis of the capability of phase differential method

在仿真实验中，信噪比为8 dB时的进动周期处理结果如图5所示。从仿真结果可以看出，相位差分法得到的进动周期更平滑和准确。由于Hilbert变换存在端点效应，进动周期数据的起始和结束部分存在显著异常，在实际应用中应该舍弃异常部分或进行进一步的处理。

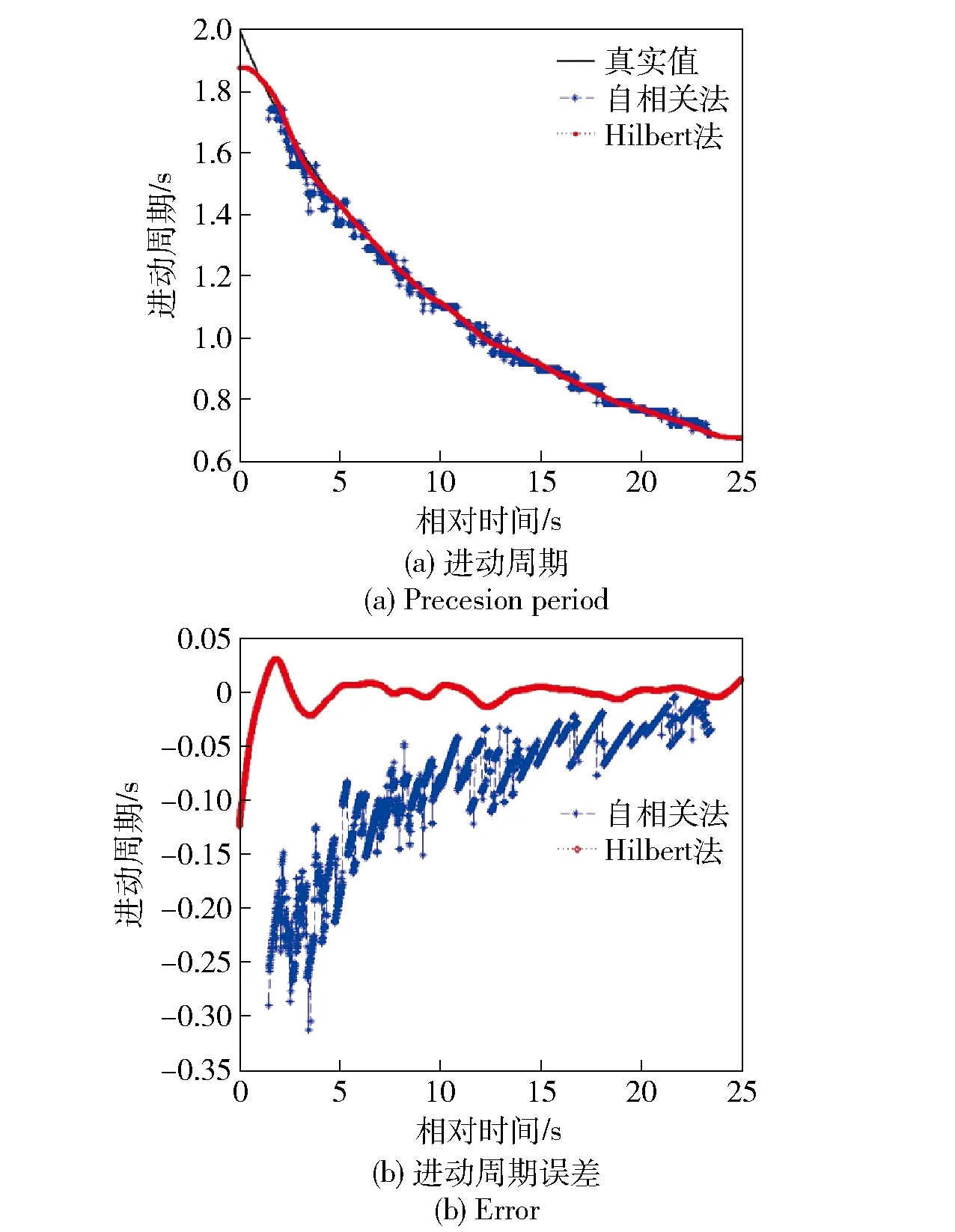
图5 进动周期与估计误差Fig.5 Precession period and estimated error

图6 实测速度Fig.6 Real radial velocity

3.2 应用分析

受雷达布站、弹道特性等影响，只有在弹道下降段，连续波雷达才能录取到进动微多普勒信号。图6为连续波雷达测量得到的某型火箭弹下降段径向速度数据，从数据曲线中可以明显看到由弹丸进动引起的准周期变化。

对速度数据进行自由节点样条函数拟合，求取质心径向速度和微动速度，如图7所示，其中微动速度包含雷达测量噪声。

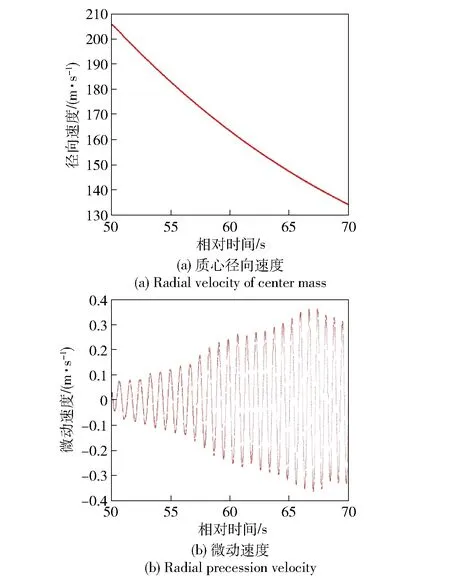
图7 质心径向速度和微动速度Fig.7 Radial velocity of center of mass and radial precession velocity

图8 微动速度相位Fig.8 Phase of radial precession velocity

对微动速度做Hilbert变换得到微动速度的解析形式，计算解析微动速度的相位，如图8中所示。微动速度的相位是连续变化的，但是直接求得的相位在±π rad之间，当相位跨越±π rad时存在从+π rad到-π rad的跳点，即存在缠绕问题。

对微动速度相位做解缠绕处理，即对从+π rad到-π rad的跳点加上±2π rad的倍数来解除缠绕现象，使微动速度的相位连续变化。由于测量误差对相位的影响较大，需要对微动速度的相位进行自由节点样条函数拟合来消除。解缠绕后的微动速度的相位及其拟合结果如图9所示。

图9 解缠绕后的微动速度相位Fig.9 Unwraped radial precession velocity phase

根据(8)式和(9)式对解缠绕和拟合后的微动速度相位处理，求取进动频率和进动周期。采用本文中的Hilbert变换方法处理的某型弹丸的进动周期如图10中红色曲线所示，图中蓝色曲线为采用文献[16]中自相关法处理得到的进动周期。两种处理方法得到进动周期的趋势非常吻合，证明了该方法的正确性和有效性。

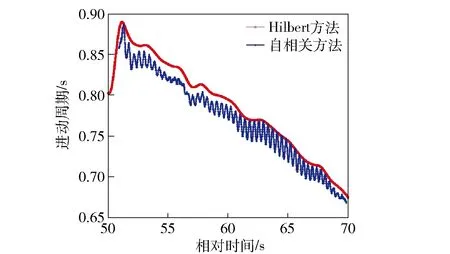
图10 进动周期Fig.10 Precession period

4 结论

弹丸在运动过程中的进动现象对雷达回波产生了微多普勒频率调制。连续波雷达测量得到的径向速度数据中包含质心径向速度和由进动引起的微动速度。对径向速度时间序列进行数据处理，利用自由节点样条函数拟合可以得到较为准确的质心径向速度分量，并由此获得微动速度，对微动速度进行Hilbert变换处理可以得到微动速度的相位信息，对相位做差分可以提取出弹丸的进动周期。仿真实验结果表明，在微动速度与速度测量误差的信噪比大于7 dB时，相位差分法更适于实际工程应用。实际试验结果表明，采用相位差分法提取的进动周期数据准确、平滑。

References)

[1] 韩子鹏. 弹箭外弹道学[M]. 北京: 北京理工大学出版社, 2008: 153-162. HAN Zi-peng. Projectile and rocket exterior ballistics [M]. Beijing: Beijing University of Aeronautics and Astronauts Press, 2008: 153-162. (in Chinese)

[2] 陈行勇. 微动目标雷达特征提取技术研究[D]. 长沙: 国防科学技术大学, 2005. CHEN Hang-yong. Research on radar signature extraction from target with micro-motions[D]. Changsha: National University of Defense Technology, 2005. (in Chinese)

[3] 陈行勇, 黎湘, 郭桂蓉, 等. 微进动弹道导弹目标雷达特征提取[J]. 电子与信息学报，2006，28(4): 643-646. CHEN Hang-yong, LI Xiang, GUO Gui-rong, et al. Radar feature extraction of micro-precession ballistic missile warhead[J]. Journal of Electronics and Information Technology, 2006, 28(4): 643-646. (in Chinese)

[4] Schultz K, Davidson S, Stein A, et al. Range Doppler laser radar for midcourse discrimination: the firefly experiments[C]∥Proceedings of the 2nd Annual AIAA SDIO Interceptor Technology Conference. Albuquerque, New Mexico: AIAA, 1993: 2653-2664.

[5] Liu L H, Wang Z , Hu W D. Procession period extraction of ballistic missile based on radar measurement[C]∥CIE International Conference on Radar. Shanghai, China: Chinese Institute of Electronics,2006.

[6] 张渊, 张爱成. 利用FFT方法分析自旋目标RCS变化周期[J].飞行器测控学报, 2012, 31(1): 26-29. ZHANG Yuan, ZHANG Ai-cheng. Analysis of the RCS variation cycle of spin-stabilized objects using FFT method[J]. Journal of Spacecraft TT & C Technology, 2012, 31(1): 26-29. (in Chinese)

[7] 陈翱. 基于RCS 序列的弹道中段目标微动提取技术[J]. 现代雷达, 2012, 34(6): 78-81. CHEN Ao. A micromoton extraction technique for target in intermediate trajectory based on RCS sequence[J]. Modern Radar, 2012, 34(6): 78-81. (in Chinese)

[8] Ross M, Shafer H. Average magnitude difference function pitch extractor[J]. IEEE Transactions on Acoustic, Speech and Signal Processing, 1974, 22(5): 355-362.

[9] 冯德军, 丹梅, 马梁. 一种鲁棒的弹道目标RCS周期估计方法[J]. 航天电子对抗, 2008, 24(2): 5-8. FENG De-jun, DAN Mei, MA Liang. A robust RCS periodicity estimation algorithm for ballistic target[J]. Aerospace Electronic Warfare, 2008, 24(2): 5-8. (in Chinese)

[10] 康猛, 王春花, 郝明, 等. 弹道目标进动周期特征提取研究[J]. 现代雷达, 2010, 32(11): 29-32. KANG Meng, WANG Chun-hua, HAO Ming, et al. A study of procession-period extraction method of ballistic target[J]. Modern Radar, 2010, 32(11): 29-32. (in Chinese)

[11] 张仕元. 基于三角函数拟合和的RCS序列进动周期估计[J].电子与信息学报, 2014, 36(6):1389-1393. ZHANG Shi-yuan. Procession period estimation of RCS sequences based on trigonometric function fitting [J]. Journal of Electronics & Information Technology,2014, 36(6):1389-1393. (in Chinese)

[12] 孟路稳, 周沫, 察豪,等. 弹道导弹目标回波模拟与微动特征提取[J].火力与指挥控制, 2015, 39(10): 1712-1715. MENG Lu-wen, ZHOU Mo, CHA Hao, et al. Echo simulation and micro-motion feature extraction of ballistic missile targets[J]. Fire Control & Command Control, 2015, 39(10): 1712-1715. (in Chinese)

[13] Chen V C. Micro-Doppler effect of micro-motion dynamics: a review[J]. Proceedings of SPIE on Independent Component Analyses, Wavelets, and Neural Networks, 2003, 5102:240-249.

[14] Chen V C, Li F, Ho S, et al. Micro-Doppler effect in radar-phenomenon, model and simulation study [J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1):2-21.

[15] 牛杰,刘永祥,秦玉亮,等. 一种基于经验模态分解的锥体目标雷达微动特征提取新方法[J].电子学报, 2011, 39(7): 1712-1715. NIU Jie, LIU Yong-xiang, QIN Yu-liang, et al. A new method of radar micro-motion feature extraction of cone target based on empirical mode decomposition[J]. Acta Electronica Sinica, 2011, 39(7): 1712-1715. (in Chinese)

[16] 李康乐, 姜卫东, 黎湘. 弹道目标微动特征分析与提取方法[J]. 系统工程与电子技术, 2010, 32(1): 115-118. LI Kang-le, JIANG Wei-dong, LI Xiang. Micro-motion feature analysis and extraction methods for ballistic target[J].Journal of Systems Engineering and Electronics, 2010, 32(1): 115-118. (in Chinese)

[17] 李益民,苏东林, 冷雪冰. 高速旋转弹丸进动周期提取[J]. 北京航空航天大学学报, 2010, 36(11): 1335-1338. LI Yi-min，SU Dong-lin, LENG Xue-bing．Precession period extraction of high-rate rotating projectile[J]．Journal of Beijing University of Aeronautics and Astronautics，2010，36(11):1335-1338. (in Chinese)

[18] 郭文胜，宫志华，董立涛，等．雷达测距拟合微分求速方法研究[J]．现代雷达，2010，32(8)：33-38． GUO Wen-sheng，GONG Zhi-hua，DONG Li-tao，et al．A study on getting radar radial velocity by range fitting and differential method[J]. Modern Radar, 2010, 32(8): 33-38. (in Chinese)

Extraction of Precession Period of Projectile Based on Phase Differential

LIU Zhi-xue, GONG Zhi-hua, LENG Xue-bing

(Baicheng Ordnance Test Center of China, Baicheng 137001, Jilin, China)

For uncontrolled projectile, such as cannonballs, rockets, etc, precession period is an important parameter of the trajectory characteristic. To obtain the precession period of projectile effectively, a precession period extraction method based on phase differential is introduced. Precession of projectile brings micro-Doppler modulation on echoes of continuous-wave radar, and its mathematic model indicates that the micro-velocity produced by precession changes with the law of sine, and the change rate of its phase is inversely proportional to precession period. The phase of the micro-velocity can be obtained by Hilbert transform, and then the precession period can be derived by the phase differential of the micro-velocity. The experimental results show that, for the micro-velocity signal which S/N is greater than 7 dB, precession period can be effectively extracted with the proposed method, and this method is more precise and smooth for actual measuring data.

ordnance science and technology; continuous wave radar; precession period; micro-Doppler; Hilbert transform

2016-04-18

刘志学(1972—),男,高级工程师。E-mail：liuzx09@qq.com

TJ012.3+6

A

1000-1093(2017)01-0177-07

10.3969/j.issn.1000-1093.2017.01.023