基于三角型模糊数理论的组合投资决策研究

周庆健，焦 佳

(大连民族大学 理学院，辽宁 大连 116605)

基于三角型模糊数理论的组合投资决策研究

周庆健，焦 佳

(大连民族大学 理学院，辽宁 大连 116605)

基于三角型模糊数理论提出一种新的组合投资决策算法。首先应用三角型模糊数描述股票的价格变化过程,采用三角型模糊数的均值面积来表示相应价格信息；然后结合投资者的具体效用函数，并假设投资收益近似服从正态分布，获得其期望效用函数；最后根据Markowitz的均值-方差模型结论确定最优组合投资收益，从而确定投资者的最优组合投资比例。该算法简洁实用，便于操作，通过给出具体应用算例说明了该算法是行之有效的。

组合投资；决策；指数效用函数；三角型模糊数

本文主要基于应用三角型模糊数来表示股票价格变化过程的理论提出一种新的组合投资决策算法。不仅对组合投资理论有一定的促进，同时对投资者进行实际操作具有一定的参考价值。

1 组合投资决策

1.1 Markowitz 的均值-方差模型

19世纪50年代，美国金融学家Markowitz提出了“组合投资理论”，该理论认为大多数风险厌恶型投资者在股票投资市场中会追求高收益的同时注意规避相应风险，并以此为基础建立了著名的均值-方差模型[1]。

设现有n种股票，它们的当前时刻(t=0)价格为S10,S20,…,Sn0,在未来某时刻(t=T)价格为S1,S2,…,Sn。

令

Xn×1=(x1,x2，…，xn)T,

式中，xi为从时刻t=0到时刻t=T的对数收益率，X为n种股票的对数收益率向量。则收益的数学期望和协方差矩阵可分别表示为

EX=(Ex1,Ex2，…，Exn)T=μ，

Var(X)=E(X-EX)(X-EX)T=Σ。

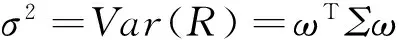
Markowitz的均值-方差模型可看作是如下一个条件极值问题[2-3]:在满足投资收益ωTμ=a条件下，求解投资比例ω使得相应风险Var(ωTX)=ωTΣω最小。经求解其最优投资比例为

(1)

相应的协方差矩阵为

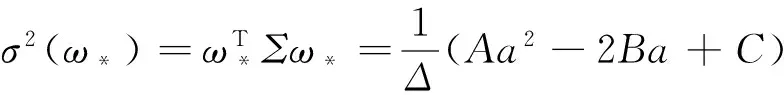
(2)

式中，A=eTΣ-1e,B=eTΣ-1μ=μTΣ-1e,C=μTΣ-1μ,Δ=AC-B2。

1.2 效用函数

在组合投资过程中，每个投资者都有属于自己的效用函数用来表示它对投资收益的满意程度，并且根据期望效用最大化原则来确定最优投资比例，从而确定投资决策方案。同时，大部分投资者为风险厌恶型，他们在追求高收益的同时规避相应风险。本文应用常见的指数型效用函数:

U=-e-kx,

式中，x为投资收益，k>0表示风险厌恶因子。

1.3 期望效用

在金融数学理论中，常假定投资收益服从正态分布N(r,σ2)，其中r,σ2分别表示期望和方差。且正态分布的密度函数为

(3)

由于该效用函数为风险厌恶型，则可应用无差异曲线法进行求解[4-5]。

1.4 三角型模糊数

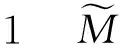
(4)

式中，l≤m≤u都为实数[6-7,9-10]。

三角型模糊数可较好的表示不确定信息，如股票未来不确定的价格过程。

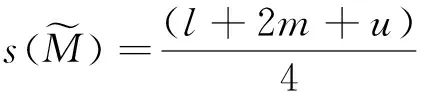
(5)

1.5 应用三角型模糊数描述股票价格变化过程

2 决策算法

基于应用三角型模糊数来表示股票价格变化过程的理论，本文提出一种新的组合投资决策算法。

2.1 数据收集与分析

2.2 求解收益率和协方差矩阵

应用式(5)得股票的相应收益率为

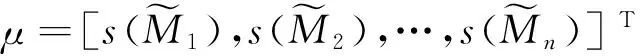
和协方差均值为

∑=(σij)n×n。

2.3 效用函数

本文采用投资学中常见的指数效用函数U(x)=-e-kx，并且其期望效用函数可求得为

2.4 最优组合投资决策

根据均值-方差模型的理论，投资者的最优组合应为投资者的无差异曲线和其有效前沿的切点，如图1。则可建立如下模型：

图1 最优组合投资的选择

进而可求得最优组合投资的比例为

3 应用

本文给出一个应用算例。假设2016年4月28日和29日，在某股票市场交易中，某位投资者有5个标的股票，其价格信息见表1。

表1 5种股票的价格信息矩阵

假设该投资者的效用函数为指数效用函数

U(x)=-e-2x，

请问该投资者该如何选择他的最优组合投资决策方案？

(1)问题分析

此问题可应用本文提出的算法来进行解决：由于股票的价格变化过程应用三角型模糊数形式给出，首先可获得其三角型模糊数均值面积；进而确定5种股票的收益率向量和协方差矩阵；然后根据投资者的效用函数，由于投资收益服从正态分布，则可获得该投资者的期望效用函数；再者根据Markowitz的均值-方差模型结论，可获得其最优组合投资收益，从而确定最优组合投资比例；最后确定该投资者针对这5种标的股票的最优组合投资方案。

(2)具体步骤

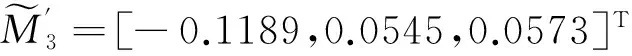
步骤2 根据式(5)确定5种股票相应的三角型模糊数均值面积，然后应用Matlab软件，获取5种股票的收益率向量和协方差矩阵：

[0.0301,-0.6853,0.2571,0.0182,-0.0001]T，

Σ=(σij)5×5=

3.0133 1.4276 0.9079 0.8264 1.4628

1.4276 0.7081 0.3573 0.3689 0.6269

0.9079 0.3573 0.4409 0.3010 0.5927

0.8264 0.3689 0.3010 0.2428 0.4484

1.4628 0.6269 0.5927 0.4484 0.8481，

同时求得A=-6.7255e+004,B=-4.4548e+004,C=-9.7906e+003,Δ=AC-B2=-1.3261e+009。

步骤3 由于其效用函数U(x)=-e-2x，则可获得其期望效用函数EU=-e[2(σ2-r)]。

解得其最优组合投资收益r=0.6623，则该投资者的最优组合投资比例为

4 结 语

应用三角型模糊数表示股票的价格变化过程，本文给出了一种新的组合投资决策算法。并给出实际算例验证了该算法简洁实用，便于操作。此算法不仅对组合投资理论有一定的促进，同时对投资者进行实际操作具有一定的参考价值。

[1]MARKOWITZH.Portfolioselection[J].JournalofFinance, 1952,7:77-91.

[2] 张尧庭. 金融市场的统计分析[M]. 广西：广西师范大学出版社,1998.

[3]SHARPEWF,ALEXANDERGJ,BAILEYJV.Investments[M].Beijing：TheChinesePeopleUniversityPress, 1998.

[4]ZHOUQJ,WUJM.Twomethodsofoptimalportfolioinvestmentwithnegativeexponentialutilityfunctionandtheirconsistency[J].JournalofDalianNationalitiesUniversity, 2004, 6(1):7-10.

[5] 李登峰. 模糊多目标多人决策与对策[M]. 北京:国防工业出版社, 2003.

[6] 周庆健，吕思瑶，焦佳,等. 双指数效用函数的组合投资决策[J]. 大连理工大学学报, 2011,51(5)：766-770.

[7]ZHOUQJ,JIAOJ,NIUDT,etal.Decision-makingofportfolioinvestmentwithlinearplusdoubleexponentialutilityfunction[J].RAIRO-OperationResearch, 2013,47:361-370.

[8]ZHOUQJ,JIAOJ,YANGDL.Theinformationentropybasedalgorithmtomultipleattributedecisionmakingwithattributevaluesintheformoftriangularfuzzynumbers[J].ICICExpressLettersPartB:Applications, 2014,5(5):1279-1284.

[9]ZHOUQJ,JIAOJ.Theorderedweightedaveragingalgorithmtomultipleattributedecisionmakingwithintriangularfuzzynumbers[J].AppliedMathematicalSciences, 2014,8(56):2763-2766.

[10]WANGTC,MENGY,MAR,etal.Themeanareameasurementmethodtomultipleattributedecisionmakingwithintriangularfuzzynumbers[J].AppliedMathematicalSciences, 2015,9(8):393-397.

(责任编辑 邹永红)

Research on Portfolio Investment Decision-making based on Triangular Fuzzy Number Theory

ZHOU Qing-jian, JIAO Jia

(School of Science, Dalian Minzu University, Dalian Liaoning 116605, China)

In this paper, one new portfolio investment decision-making algorithm is proposed according to the triangular fuzzy number theory. Firstly, in the security portfolio investment progress, the triangular fuzzy number is used to express the security price changing process. Secondly, the mean area of the triangular fuzzy number is adopted to express the security price information. Thirdly, combining with the investor’s specific utility function, and supposing that the investment return approximately obeys the normal distribution, the investor’s expectation utility function can be determined. Finally, according to the conclusion of Markowitz’s Mean-Varianc Model, the optimal portfolio investment return can be got, and the optimal portfolio investment proportion can be determined. This algorithm is concise, practical and easy to operate. In the last, an illustrative example is given to prove that the decision-making algorithm proposed in the paper is feasible and valid.

portfolio investment; decision-making; exponential utility function; triangular fuzzy number

2016-11-07；最后

2016-11-24

辽宁省教育厅项目(L2014549,LJQ2015029)；辽宁省科技厅项目(2015020021，201601088)；中央高校基本科研业务费专项资金资助项目(DC201502050304,DC201502050409,DC201501043,DCPY2016058,DCPY2016061)；大连民族大学人才启动基金资助项目(110090)。

周庆健(1978-)，男，山东邹城人，副教授，博士，主要从事金融数学和决策管理研究。

焦佳(1982-)，女，河南焦作人，副教授，博士，主要从事微分方程和决策管理研究，jiaojia@dlnu.edu.cn。

2096-1383(2017)01-0059-04

O

A