气囊式火星着陆器稳健性优化设计

卿启湘 卿 翔 肖久如 廖惠东1.湖南大学特种装备先进技术与仿真教育部重点实验室，长沙,4100822.湖南大学汽车车身先进设计制造国家重点实验室，长沙,410082.中南林业科技大学机电工程学院，长沙，410004

气囊式火星着陆器稳健性优化设计

卿启湘1,2卿 翔1,2肖久如1,2廖惠东3
1.湖南大学特种装备先进技术与仿真教育部重点实验室，长沙,4100822.湖南大学汽车车身先进设计制造国家重点实验室，长沙,4100823.中南林业科技大学机电工程学院，长沙，410004

气囊式火星着陆器结构复杂，关键参数多，工况极端，不确定因素多且可靠性要求高。针对气囊式火星着陆器优化设计中的计算效率问题，采用基于超级计算平台并行分布式计算技术与稳健性优化设计理论的多目标稳健性优化方法对复杂气囊系统进行了稳健性优化设计。结果表明：超级计算平台的应用使稳健性优化的计算效率得到了显著提升；稳健优化设计后的气囊式火星着陆系统的可靠性有明显改善。

6σ稳健性优化；气囊；超级计算平台；火星着陆器

0 引言

缓冲气囊是一种常用的着陆缓冲装置，它可以有效地减小装备着陆时的冲击载荷, 在航天器软着陆工程中应用极其广泛[1-2]。气囊以其质量轻、性能可靠、制造方便、成本低等优点被广泛用于汽车安全与着陆缓冲等技术领域[3]。近年来国内外学者展开了大量的关于气囊着陆缓冲方面的研究工作。TAYLOR[4]采用LS-DYNA对BeagleⅡ火星探测器的气囊着陆缓冲过程进行了模拟，通过仿真得到了不同工况下的着陆冲击响应。文桂林等[5]采用LS-DYNA对全向式多室连通气囊的缓冲特性进行了研究并完成了该气囊系统的优化设计。何欢等[6]利用地面原理样机冲击响应与外星环境下全尺寸气囊着陆系统冲击响应的动力学相似关系获得了火星环境下的全尺寸气囊系统着陆冲击响应。气囊式火星着陆系统在设计和制造过程中，有许多不确定因素，如果由于不确定因素估计不足而导致缓冲着陆的安全性方面的问题，这将会对整个着陆工程带来巨大的损失，甚至是毁灭性的。由于传统的确定性优化设计忽略了不确定因素的影响，导致火星着陆器着陆缓冲过程的安全性不稳健[7]，因此在火星着陆气囊系统的优化设计中，必须考虑不确定因素对气囊式着陆缓冲系统缓冲性能的影响，进行稳健性分析。

针对传统确定性设计的不足，国内外学者对不确定性分析和设计的理论和方法展开了大量的研究工作。MYERS等[8]提出了双响应面法，其后VINING等[9]对其进行改进来解决稳健设计中的参数设计问题，提出同时优化均值和方差两个响应的思想。KHURI 等[10]提出了广义距离函数法，采用响应的方差——协方差来估计各个响应与其最优值之间距离的权重，以最小化广义距离确定最佳的操作条件，能够消除方差和交互作用负面影响。HARRINGTON[11]最早提出了满意度函数法[12]，后来DERRINGER等[13]对该方法进行了改进，可以根据经验设置不同的参数以调节各响应偏离目标值的程度。

近年来国内外学者展开了大量有关超级计算的理论和应用的研究。丁峻宏等[14]基于高性能计算的CAE技术对大型盾构施工过程进行了仿真。范晓樯等[15]针对超声速/高超声速飞行器绕流流场问题，在超级并行计算机上基于有限体积方法、TVD差分格式和显式Runge-Kutta迭代方法的框架完成了264个CPU并行数值计算工作。杜新光等[16]在上海超级计算中心的曙光4000A上完成了基于接触均衡的并行分区算法的仿真计算，解决了模型庞大带来的求解困难问题，求得了轻轨车辆在大跨度斜拉桥上运行的轮轨横向和垂向接触力。

本文在前人基础上，以气囊式火星着陆系统作为研究对象，并考虑气囊结构设计参数的不确定性，基于超级计算平台(简称超算平台)获取了气囊式火星着陆器的响应面近似模型，并结合多目标优化算法及稳健设计理论对气囊式火星着陆系统进行了稳健性优化设计，获得了可靠性更高的稳健优化设计结果。

1 计算方法

1.1 响应表面法[17]

气囊式火星着陆器的着陆缓冲过程仿真分析是一个强非线性冲击问题，涉及力学分析中的几何非线性、材料非线性及边界条件非线性等。响应表面法采用试验设计方法获取设计样本点，并对设计样本点进行计算，得到其目标函数和约束函数的响应面模型，从而用来预测其他点的响应值。在对气囊式火星着陆器进行耐撞性优化的过程中如采用优化算法直接调用有限元模型进行优化，就会使得优化计算十分耗时，甚至难以完成，而基于近似模型的优化具有求解时间短、求解效率高等优点。因此，本文采用多项式函数近似模型的方法，根据试验设计样本点信息，获得设计变量和目标函数或约束函数之间的数学函数模型。

多项式函数模型可以表达为如下形式：

(1)

其中，p表示多项式函数项φi(x)的项数,x为设计变量，βi为多项式函数项φi(x)的系数，βi的值可采用最小二乘法获取。根据有限元仿真获得的m(m>p)个采样点xj的响应值yj(j=1, 2,…,m)构造最小二乘函数如下：

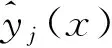
b=(ΦTΦ)-1ΦTy

(3)

其中，y为响应值列向量，y=(y1,y2,…,ym)T。Φ为m个采样点处多项式函数项所形成的矩阵，该矩阵可以表示为

(4)

把式(3)代入式(1)中，可以获得多项式函数模型。空间设计变量x与响应Y的函数关系为

(5)

其中，ε为误差项。

本文建立了一阶到四阶近似模型并选取误差最小的四阶多项式响应面近似模型来进行优化设计。

1.2 全因子试验设计法

本文采用全因子试验设计方法来进行样本点采样。假如因素(设计变量)个数为k，每个因素的水平为q，则全因子法的试验次数为kq。

在设计变量不多的情况下，全因子法是一种有效的试验设计方法。图1给出了三因素三水平的全因子法采样点(图中黑实点)的分布，总试验次数为27。

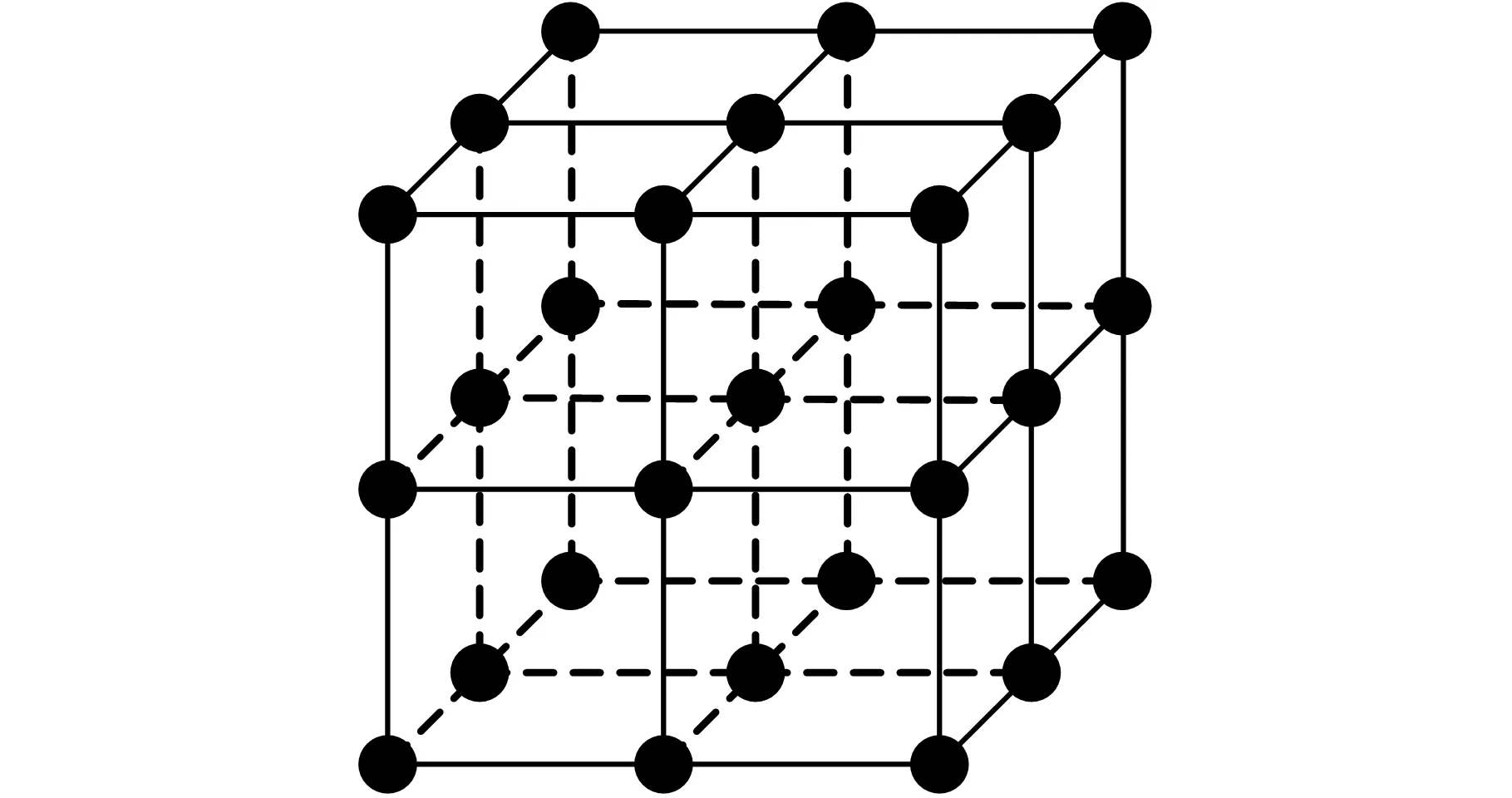
图1 三因素三水平的全因子法采样点分布Fig. 1 The sampling points distribution of three factors and three levels of full factorial method

1.3 多目标粒子群算法[18]

到目前为止，一些多目标算法已经得到了很好的发展。例如：非支配排序遗传算法Ⅱ(NSGA-Ⅱ)、多目标粒子群优化(MOPSO)算法、多目标的人工蜂群算法(MOABC)。粒子群优化算法是一种基于群智能启发式全局随机优化算法，相对于传统的多目标优化方法，粒子群优化算法在解决多目标优化问题上具有很大的优势[19]。该算法参照群体中目前处于最优位置的个体和自身曾经到达的最优位置来调整下一步的搜寻方向和大小。且粒子群优化算法的通用性比较好，适合处理多种类型的目标函数和约束，容易与传统的优化方法相结合，从而改进自身的局限性，达到更高效率的解决问题。

1.4 蒙特卡罗模拟技术[20]

蒙特卡罗(MCS)方法原理是基于大量试验中目标事件发生的频率来估算其发生概率。通过对随机变量的大量随机抽样，并根据抽样组合计算结构功能函数值，从而依据事件发生的次数计算得到结构的可靠度。蒙特卡罗方法无需考虑功能函数的非线性和极限状态曲面的复杂性，有效回避了结构可靠性分析中的数学困难。且随着模拟次数的增加，通过蒙特卡罗方法计算得到的可靠度趋近于精确解，该方法被认为是一种准精确的方法，所以通常采用该方法来验证其他近似计算方法的准确性。气囊式火星着陆器设计参数的不确定性是本研究的主要出发点，不仅要实现最佳的性能指标或目标，还需适应由于不确定性引起的性能变化。因此，本文采用基于蒙特卡罗模拟技术的6σ稳健性优化方法对气囊式火星着陆器进行优化设计。

2 多目标确定性与稳健性优化

2.1 确定性优化

通常情况下，多目标优化(multi-objective optimization, MOO)问题没有单一的解决方案。取而代之的是一组反映目标中不同层次权衡的解决方案。从数学上表示确定性MOO问题，即

(6)

式中,f(x)为目标矢量；gj(x)为约束函数；M为约束的个数；xL和xU分别为设计变量x的下限和上限。

在确定性优化过程中没有考虑不确定因素可能会导致不可靠的设计，因此，需要解决由于过于敏感设计参数的微小变化导致的性能显著损失。

2.2 6σ稳健性优化

基于蒙特卡罗的6σ稳健性设计是摩托罗拉公司提出的为提高产品质量的设计方法。其中6σ概念是一种为提高产品质量的现代质量管理方法，σ为标准差,被用于定量描述产品质量特性总体对目标值的偏离程度。

在实际生产过程中，产品的性能不可能长时间都保持在一个水平上，随着时间的推移，废品出现的概率增大。如制造一个零件的尺寸为10，而这个零件具有±0.1的误差，当加工过程的每一个环节完全满足这个尺寸时，仍然存在刀具的磨损，加工尺寸会改变，这就会引起性能波动的漂移，摩托罗拉等公司将此漂移量设定为1.5σ。表1列出了相应σ水平的变异百分比和每百万的缺陷数。目前多数制造业采用的质量控制目标是±3σ，而±3σ的质量控制目标对于一些行业是无法满足的。如果提升到±6σ水平，产品的质量会得到几十倍的提高，因此，采用±6σ质量水平作为设计标准对提高产品质量具有重要意义。

表1 变异的百分比和每百万的缺陷数
Tab.1 The percentage of variation and the defects number per million

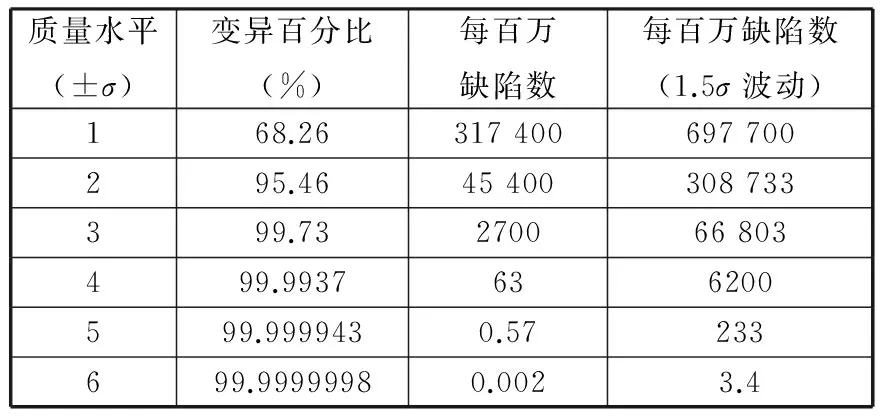
质量水平(±σ)变异百分比(%)每百万缺陷数每百万缺陷数(1.5σ波动)168.26317400697700295.4645400308733399.73270066803499.9937636200599.9999430.57233699.99999980.0023.4

多目标稳健优化数学模型可描述为

(7)

式中, μfk(x)、σfk(x)分别为不同优化目标函数的均值和标准差；μgj(x)、σgj(x)分别为第j个约束的均值和标准差；μxi、σxi分别为设计变量的均值和标准差；m为期望的σ水平，基于蒙特卡罗的6σ稳健性设计优化中，m=6。

3 气囊式火星着陆器气囊耐撞性优化

气囊式火星着陆器耐撞性指标主要包括：探测器质心峰值加速度、气囊峰值压力和比吸能等。本文采用探测器质心峰值加速度、气囊峰值压力作为评价指标以评价气囊式火星着陆器结构的耐撞性。

3.1 模型的建立

着陆器在着陆过程中4个面均被气囊所包裹，气囊在触地反弹过程中起到缓冲作用以保证着陆器内装备的安全。

根据气囊式火星着陆器的几何尺寸(气囊直径为353 mm)在SolidWorks里面建立着陆舱和单侧气囊三维模型并完成整体装配，然后将建好的几何模型导入到Hypermesh软件进行网格的划分，有限元模型如图2所示。模型中气囊、着陆舱、加强绳、地面等材料分别使用*PIECEWISE_LINEAR_PLASTICITY、*FABRIC、*SEATBELT和*SOIL_CONCRETE关键字进行定义。采用*AIRBAG_WANG_NEFSKE及*AIRBAG_INTERACTION关键字分别对气囊系统及气囊之间的连通进行定义。

图2 火星着陆气囊系统的有限元模型Fig. 2 The finite element model of mars lander airbag system

3.2 优化过程及结果

根据设计要求采用全因子采样的方式进行试验设计，并应用商业软件LS-DYNA对上述建立的有限元模型进行并行计算。本文采用的并行计算机是曙光刀片机，为寻求最优的计算效率,本文分别对不同计算核数目下的加速比Sp和并行效率Ep进行对比分析，其中Sp和Ep的计算表达式如下：

(8)

式中，ts为单个处理器的计算时间；tp为多个处理器的计算时间，包括各处理器的计算开销和处理器之间的通信开销；n为计算采用的处理器数量。

不同计算核数量下计算效率对比如表2所示，在CPU个数为32以内时，随着CPU个数的增加计算时间不断缩短，加速比也逐渐增大，然而并行效率却逐渐降低，而采用64核进行计算时计算时间反而延长，这是由于各计算节点间的通信开销增大导致的，而较为合理的CPU个数的分配为每个CPU分配1万至5万个单元。本文有限元模型共有20万个单元，因此本文均采用16核对此模型进行计算与分析。整个多目标优化设计流程如图3所示。

表2 并行效率分析

Tab. 2 Parallel efficiency analysis

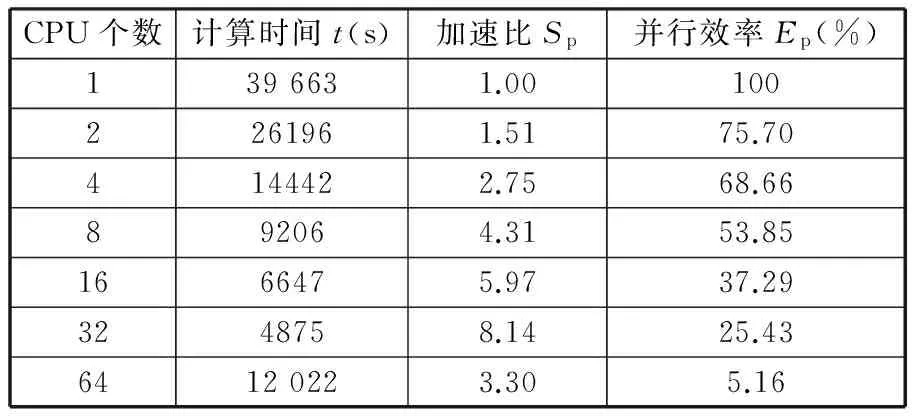
CPU个数计算时间t(s)加速比Sp并行效率Ep(%)1396631.001002261961.5175.704144422.7568.66892064.3153.851666475.9737.293248758.1425.4364120223.305.16

研究了气囊式火星着陆缓冲器在不考虑设计变量中噪声因素波动性的确定性优化数学模型，可描述为

(9)

式中，ap为探测器质心峰值加速度；pe为气囊峰值压力；p0为初始压力;D1为气囊系统内部的通气孔直径；D2为气囊系统之间的通气孔直径。

考虑到加工工艺因素，本文取加工精度为其变化区间的5%，因此对应的稳健性优化数学模型可描述如下：

(10)

采用多目标粒子群优化算法对式(9)、式(10)的多目标优化问题进行计算。在粒子群算法中，惯性权重c0=0.4，加速因子c1=c2=1.0，种群大小p=500，解集合数量A=50。当迭代次数为500时，Pareto前沿已经收敛。而在稳健性优化过程中，每个设计变量的采样点按照正态分布随机抽样得到1000个蒙特卡罗样本点，并将1000个样本点代入构建的四阶多项式代理模型中去获取目标函数的均值和方差，最后采用多目标粒子群算法对式(10)进行求解，得到稳健性优化的Pareto最优解集，如图4所示。通过对比可以发现稳健性优化的Pareto最优解集在同等约束条件下要比确定性优化解稍大一些，这是由于稳健性优化考虑了设计变量的不确定性。

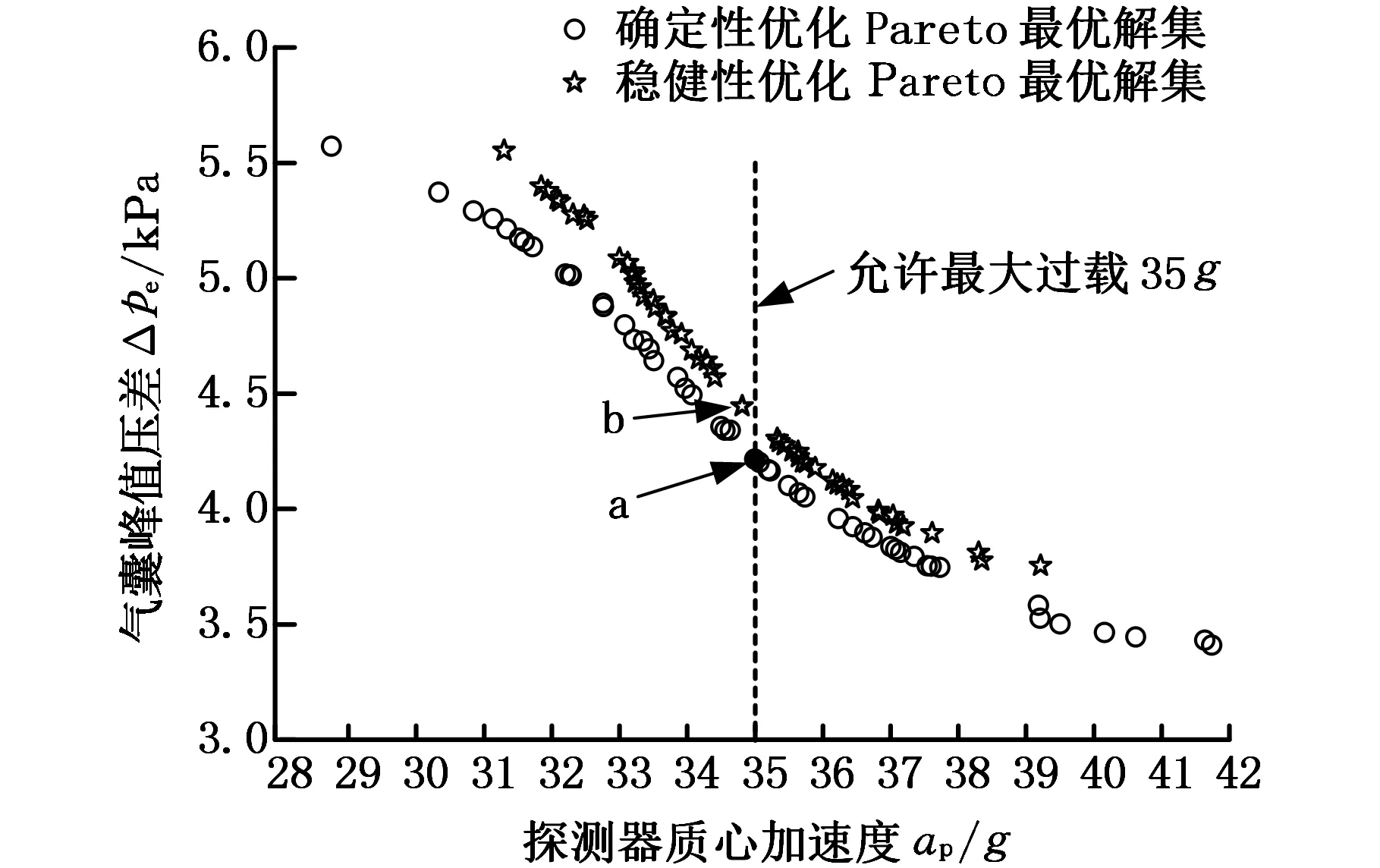
图4 确定性优化和稳健性优化的Pareto前沿Fig. 4 The Pareto frontier of deterministic and robustness optimization

如果实际设计中要求探测器质心峰值过载小于35g，则分别取图4中的a点和b点作为确定性优化和稳健性优化的优化设计点，对应的优化结果如表3所示。虽然稳健性优化的气囊峰值压差4.44 kPa比确定性优化的4.216 kPa要大，但是峰值过载的可靠度却由确定性优化的73.4%提高到了100%，通过稳健性优化设计后，不仅目标函数的响应波动减小了，而且峰值过载ap响应分布的6σ水平落在约束界限范围内，显著提高了产品质量的稳定性和可靠性。

表3 优化设计结果对比
Tab. 3 The contrast of optimization results

参数确定性最优解稳健性最优解设计变量初始压力p0(kPa)6.30935.826内孔直径D1(mm)72.65268.836通气孔直径D2(mm)90.00086.992约束条件ap<35g峰值过载ap(g)34.99834.812可靠度(%)73.4100目标函数pe(kPa)气囊峰值压差Δpe4.2164.444均值μ4.3044.304方差σ0.02200.0222

为了验证优化解的准确性，构建了稳健性优化和确定性优化的最优设计点对应的气囊式火星着陆器有限元模型(本有限元模型的准确性已经被试验所验证[21])。稳健性优化设计点的仿真结果为：探测器峰值过载和气囊峰值压差分别是34.8260g和4.363 kPa，这与优化解的34.812g和4.444 kPa仅相差0.04%和1.8%，这说明优化解精度能满足工程设计要求。通过仿真计算得到探测器过载以及气囊压力曲线,如图5和图6所示。

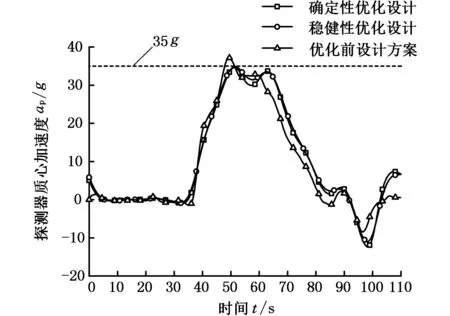
图5 稳健性和确定性优化最优设计工况探测器过载曲线Fig.5 The detector overload curve under the condition of robustness and deterministic optimization optimal design

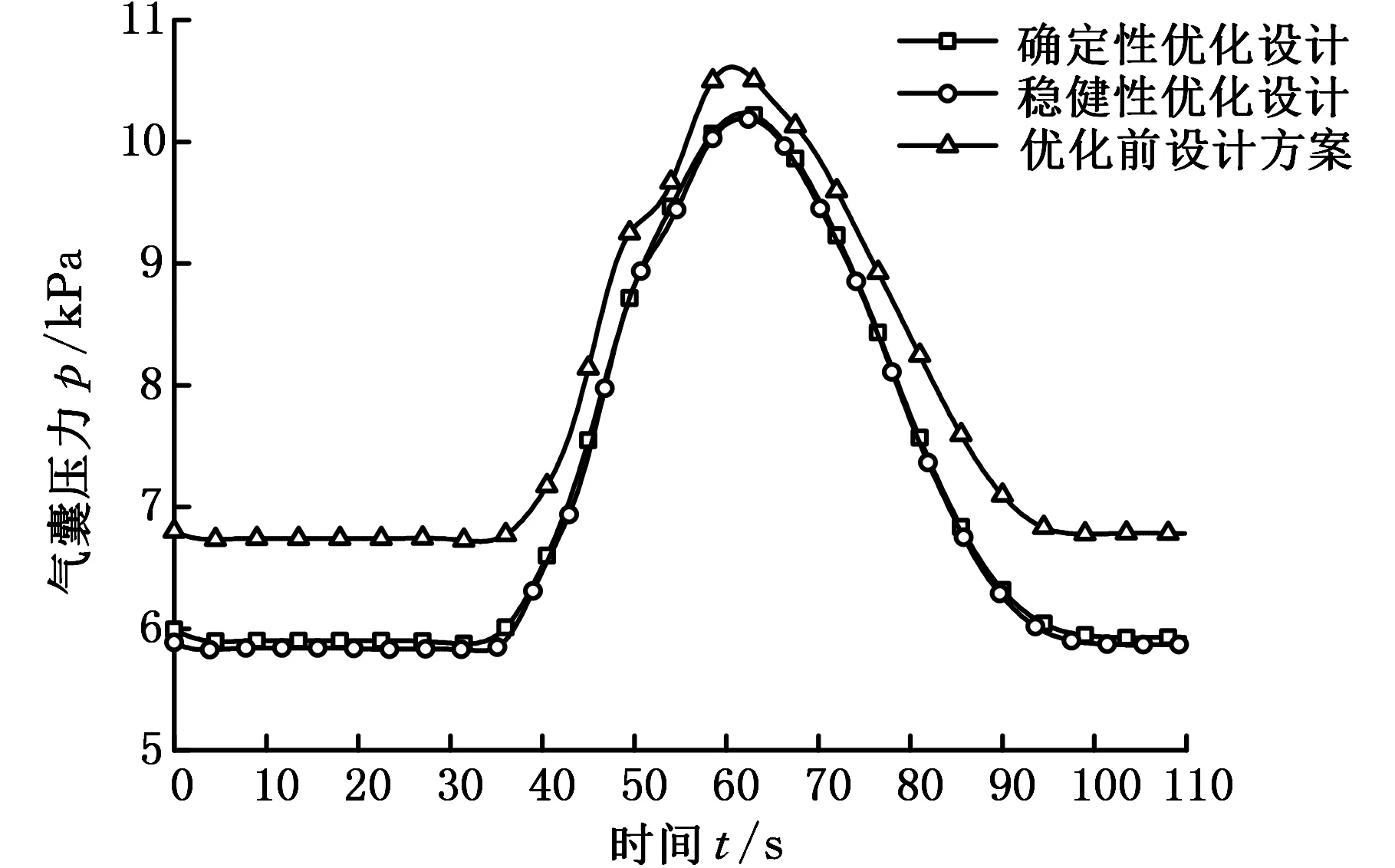
图6 稳健性和确定性优化最优设计工况气囊压力曲线Fig.6 The airbag pressure curve under the condition of robustness and deterministic optimization optimal design

从图5可以看出，稳健优化后设计方案能满足过载小于35g的要求。根据表3，稳健优化方案的可靠性也能满足工程设计要求。将稳健性优化得到的最优点与确定性优化结果相比较，虽然过载峰值都满足过载ap<35g的要求，但是稳健优化结果的可靠性比确定性优化的可靠性要高很多。所以，基于多项式代理模型的6σ稳健性优化设计方法能够很好地解决气囊式火星着陆系统的稳健性优化设计问题。

4 结论

(1)通过对气囊式火星着陆器的确定性和稳健性优化设计的对比发现，稳健性优化最优解b点所在处的气囊峰值压力4.44 kPa比确定性优化最优解a点所在处的4.216 kPa稍大一点，然而可靠度却从73.4%提高到了100%。通过稳健性优化设计后，不仅使目标函数的响应波动减小了，而且峰值过载ap响应分布的6σ水平落在约束界限范围内，产品质量的稳定性和可靠性得到了显著提高。

(2)本文基于超算有限元仿真、响应面模型、蒙特卡罗模拟、6σ稳健设计理论和多目标粒子群算法提出了适合复杂结构设计的稳健性优化方法，并采用该方法对气囊式火星着陆器进行了多目标稳健优化设计。

(3)采用基于超算平台的并行计算可以大大提高计算速度，但是当核数增加到64核时，通信开销的增大会严重影响计算的速度。这是因为在模型分区的时候每个部分的单元数在1万至5万个的范围较为合理，因此可以通过对并行效率的分析与有限元模型的规模来合理选择计算采用的CPU个数。

[1] STEIN J，SANDY C. Recent Developments in Inflatable Airbag Impact Attenuation Systems for Mars Exploration[C]// 44th AIAA/ASME/ASCE/AHS Structures，Structural Dynamics，and Materi-als Conference. Norfolk，Virginia，2003：1-6.

[2] NORTHEY D，MORGAN C. Improved Inflatable Landing Systems for Low Cost Planetary Landers[J]. Acta Asrtonautica，2006，59：726-733.

[3] 戴华杰，胡振东，咸奎成. 火星探测器气囊缓冲系统着陆过程仿真[J]. 力学季刊，2010，31(4)：555-561. DAI Huajie，HU Zhendong，XIAN Kuicheng. Simulation Analysis for Landing Process of a Mars Detector with Airbag Buffer System[J]. Chinese Quarterly of Mechanics，2010，31(4)：555-561.

[4] TAYLOR A P. Design Optimization of the Beagle Ⅱ Mars Lander Airbags through Explicit Finite Element Analysis—An Update[C]//Proc. of 6th International LS-DYNA Users Conference. Michigan，2000:15-28.

[5] 文桂林，雷志华，尹建武，等. 全向式多室连通气囊的缓冲特性研究[J]. 振动与冲击，2013，32(8)：13-17. WEN Guilin，LEI Zhihua，YIN Jianwu，et al. Cushion Characteristics of an Omni-directional and Multi-chamber Airbag[J]. Journal of Vibration and Shock，2013，32(8)：13-17.

[6] 何欢，何成，陈国平，等. 深空探测气囊着陆缓冲系统的原理样机冲击动力学相似问题研究[J]. 振动与冲击，2013，26(4)：554-560. HE Huan，HE Chen，CHEN Cuoping，et al. Similarity Problem of the Impact Response of the Deep Space Exploration Airbag Cushion Landing System and Its Prototype[J]. Journal of Vibration and Shock，2013，26(4)：554-560.

[7] 刘德顺，岳文辉，杜小平. 不确定性分析与稳健设计的研究进展[J]. 中国机械工程，2006，17(17)：1834-1841. LIU Deshun，YUE Wenhui，DU Xiaoping. Study on Uncertainty Analysis and Robust Design: a Review[J]. China Mechanical Engineering，2006，17(17)：1834-1841.

[8] MYERS R H，CARTER W H. Response Surface Techniques for Dual Response Systems[J]. Technometrics，1973，15：301-317.

[9] VINING G G，MYERS R H. Combining Taguchi and Response Surface Philosophies：a Dual Response Approach[J]. Journal of Quality Technology，1990，22(1)：38-45.

[10] KHURI A I，CONLON M. Simultaneous Optimization of Multiple Responses Represented by Polynomial Regression Functions[J]. Technometrics，1981，23(4)：363-375.

[11] HARRINGTON E C. The Desirability Function[J]. Industrial Quality Control，1965，21：494-498.

[12] 王晶. 基于响应曲面法的多响应稳健性参数优化方法研究[D]. 天津：天津大学，2009. WANG Jing. Robust Parameter Optimization for Multi-response Using Response Surface Methodology [D]. Tianjin：Tianjin University，2009.

[13] DERRINGER G C，SUICH R. Simultaneous Optimization of Several Response Variables[J]. Journal of Quality Technology，1980，12：214-219.

[14] 丁峻宏，李根国，金先龙，等. 基于高性能计算的 CAE 技术在大型盾构施工仿真中的应用[J]. 计算机辅助工程，2011，20(1)：163-167. DING Junhong，LI Genguo，JIN Xiaolong，et al. Application of CAE Technology Based on High Performance Computing in Large-scale Shield Construction Process[J]. Computer-aided Engineer-ing，2011，20(1)：163-167.

[15] 范晓樯，李桦，李晓宇，等. 超声速飞行器流场的并行数值计算及效率分析[J]. 国防科学技术大学学报，2006，28(3)：1-4. FAN Xiaoqiang，LI Hua，LI Xiaoyu，et al. Parallel Numerical Simulation and Efficiency Analysis of the Flow Field of Supersonic Vehicle[J]. Journal of National University of Defense Technology，2006，28(3)：1-4.

[16] 杜新光，金先龙，陈向东. 基于并行计算的大跨度斜拉桥行车安全分析[J]. 振动与冲击，2010，29(7)：5-8. DU Xinguang，JIN Xianlong，CHEN Xiangdong. Simulation Analysis for Running Safety of a Light- rail Train on a Long Span Cable-stayed Bridge Based on Parallel Computation[J]. Journal of Vibration and Shock，2010，29(7)：5-8.

[17] ZHAO Jieliang， YAN Shaoze, WU Jianing. Analysis of Parameter Sensitivity of Space Manipulator With Harmonic Drive Based on the Revised Response Surface Method[J]. Acta Astronautica，2014，98：86-96.

[18] ZHAO Qiang，YAN Shaoze . Collision-free Path Planning for Mobile Robots Using Chaotic Particle Swarm Optimization[J]. Lecture Notes in Computer Science，2005， 3612：632-635.

[19] 薛洪波，伦淑娴. 粒子群算法在多目标优化中的应用综述[J]. 渤海大学学报(自然科学版)，2009，13(3)：265-269. XUEHongbo, LUN Shuxian. A Review on Appliaction of PSO in Multi-objective Optimization[J]. Journal of Bohai University ( Natural Science Edition)，2009，13(3)：265-269.

[20] GUO Pengfei. Kinematic Accuracy Analysis of Flexible Mechanisms with Uncertain Link Lengths and Joint Clearances[J]. Journal of Mechanical Engineering Science, 2011,225(8):1973-1983.

[21] 文桂林,肖久如,尹汉锋,等.全向式多室连通火星着陆缓冲气囊的多目标优化设计[J]. 机械工程学报,2015,51(15):135-141. WEN Guilin，XIAO Jiuru，YIN Hanfeng，et al. Multi-objective Optimization Design of Omni-directional Multi-chamber Airbag for Landing on Mars[J].Journal of Mechanical Engineering,2015,51(15):135-141.

(编辑 袁兴玲)

Robust Optimization Design of the Mars Airbag Lander

QING Qixiang1,2QING Xiang1,2XIAO Jiuru1,2LIAO Huidong3

1.The Key Laboratory of Advanced Design and Simulation Techniques for Special Equipment of MOE,Hunan University, Changsha, 410082 2.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha, 410082 3.Mechanical and Electrical Engineering, Central South University of Forestry and Technology,changsha，410004

Mars airbag lander was a complex structure with many critical parameters, extreme environment conditions, many uncertain factors and high reliability requirements. Computational efficiency of simulation was always a bottleneck problem in the processes of optimization design for the Mars airbag landers. Based on parallel and distributed computing technologies of super computing platforms and the multi-objective robust optimization method, a robust optimization design for the complex airbag system was carried out. The results show that the applications of supercomputer platform may greatly improve the robust optimization’s computational efficiency in the optimization design, and the reliability of the Mars airbag lander will be highly improved.

6σrobust design；airbag；supercomputing platform；Mars lander

2015-12-04

高等学校博士学科点专项科研基金资助项目(20120161130001)；国家杰出青年科学基金资助项目(11225212)；国家科技支撑计划资助项目(2012BAH09B02)

V476

10.3969/j.issn.1004-132X.2017.01.004

卿启湘，男，1964年生。湖南大学特种装备先进技术与仿真教育部重点实验室副教授。主要研究方向为特种车辆与特种装备设计与开发。已发表论文30余篇。卿 翔(通信作者)，男，1990年生。湖南大学特种装备先进技术与仿真教育部重点实验室硕士研究生。E-mail:qingxiang3354@163.com。肖久如，男，1989年生。湖南大学特种装备先进技术与仿真教育部重点实验室硕士研究生。廖惠东，男，1990年生。中南林业科技大学机电工程学院硕士研究生。