一种考虑应力梯度的疲劳寿命预测方法

申杰斌 唐东林西南石油大学机电工程学院，成都，610500

一种考虑应力梯度的疲劳寿命预测方法

申杰斌 唐东林
西南石油大学机电工程学院，成都，610500

针对临界距离法及应力场强法在疲劳寿命预测过程中存在的问题，结合临界距离法计算量小、应力场强法能够反映构件所处应力状态的优点，提出了以缺口附近球形区域内的等效应力均值作为控制疲劳行为的当量应力的方法。参照一组疲劳试验对当量应力与球形区域半径的关系进行了研究，结果表明可用线性和指数函数的形式表示两者间的关系。通过定义应力梯度、相对应力梯度，构建了一种能够考虑应力梯度的疲劳寿命预测模型。对模型中参数的确定方法进行研究，提出了以光滑试件、缺口试件在各自相同载荷条件的疲劳极限作用下，两者当量应力相等时的球形区域半径作为损伤区域大小的方法，该方法不再需要通过试验获得半径参数，具有较强的实用性。疲劳试验结果表明，模型预测结果均在2倍分散带内，证明模型具有较好的预测精度，同时模型可准确预测疲劳破坏位置。

缺口；应力梯度；应力分布；疲劳寿命预测

零部件产生应力集中，因此缺口往往控制着整个结构件的强度和寿命，对应力集中部位的疲劳寿命评估也成为抗疲劳设计的关键。在疲劳研究史上，许多学者逐渐注意到应力集中部位的疲劳行为并不唯一由缺口处最大应力控制，而是与缺口根部有限体积内的应力应变分布及应力梯度有关，因此一般定义缺口局部损伤区应力场中的某一特征应力应变作为控制缺口疲劳寿命的参数。典型的方法有临界距离法、应力场强法和名义应力法。临界距离法[1-3]考虑了缺口附近的应力分布状态，将缺口最大主应力处某一临界距离内(一定距离内的点或线)的平均应力作为控制缺口疲劳行为的有效应力。但临界距离法只考虑了局部区域内的最大主应力，因此对于构件的多轴应力状态不能取得精确的预测结果；同时临界距离被认为是材料常数，但有研究[4-5]指出临界距离与缺口的应力集中系数kt是相关的，因此该方法的预测稳定性仍需作进一步研究。应力场强法[6-7]考虑了缺口附近局部区域内各点距应力峰值点的距离、方向角、各点应力状态、应力梯度等，通过对局部区域内各点等效应力值进行加权数学处理来定义控制参数应力场强，在得到应力场强σfi后，由材料的S-N曲线计算缺口构件的疲劳预测寿命。但该方法中，局部损伤区域Ω′的大小需通过试验确定[8]；局部区域内对各点共同作用的等效应力函数(对韧性材料而言)f(σij)及其权函数φ(r′)，无论通过弹塑性理论计算，还是通过仿真获得结果，计算量都较大[9]；区域内各点应力梯度难以计算，以各点与应力峰值的相差程度来代替也不够准确。以上因素造成应力场强法虽然预测精度较高但是不易用于实际构件的寿命预测。

名义应力法[10-12]假定：对于相同材料制成的任意构件，只要其应力集中系数、载荷谱相同则它们的寿命相同。疲劳破坏是一种局部高应力区的行为，但名义应力法定义的是构件截面上的平均应力，且没有考虑缺口根部局部塑性变形的影响，因而名义应力法与疲劳机理不符，预测结果不稳定，精度较低。

本文在已有研究的基础上提出一种能够考虑缺口附近局部区域内的整体应力梯度且易实施的疲劳寿命预测方法。

1 疲劳寿命预测模型的构建

定义以应力峰值点为球心的球形区域内的等效应力均值作为控制疲劳行为的当量应力，有

(1)

式中，σav为当量应力；Ω为局部损伤区域，是以应力峰值点为球心、半径为r的球形区域；V为Ω的体积；σeq(r)为一定半径的球形区域内各点的等效应力值。

得到当量应力σav后，由材料S-N曲线计算疲劳寿命预测结果。与名义应力法相较，该模型考虑了局部损伤区域内应力应变及应力梯度，不再是整个截面的平均应力值，更加符合疲劳机理，同时也能考虑局部塑性变形的影响；与临界距离法相较，该模型考虑的是等效应力均值，能够反映工程构件的多轴应力状态；与应力场强法相较，该模型考虑因素少了各点距应力峰值点的距离、方向角及各点应力梯度，计算成本低。

2 应力梯度的研究

选取一组疲劳试验[10，13]对缺口附近区域的整体应力梯度进行研究。试件材料为LY12-CZ，厚度为2 mm，分别为双孔试件DH-A、DH-B和双边缺口试件DN-A、DN-B。结构尺寸分别见图1、表1。试件所受载荷、约束参照疲劳试验过程中的设定，采用ANSYS有限元分析获得缺口附近应力场，在ANSYS后处理程序中对应力场数据进行数学处理，计算得到当量应力σav。处理方式：分别取半径r不同的球形区域，计算不同缺口处附近球形区域内当量应力σav，σav与r的关系如图2～图5所示。

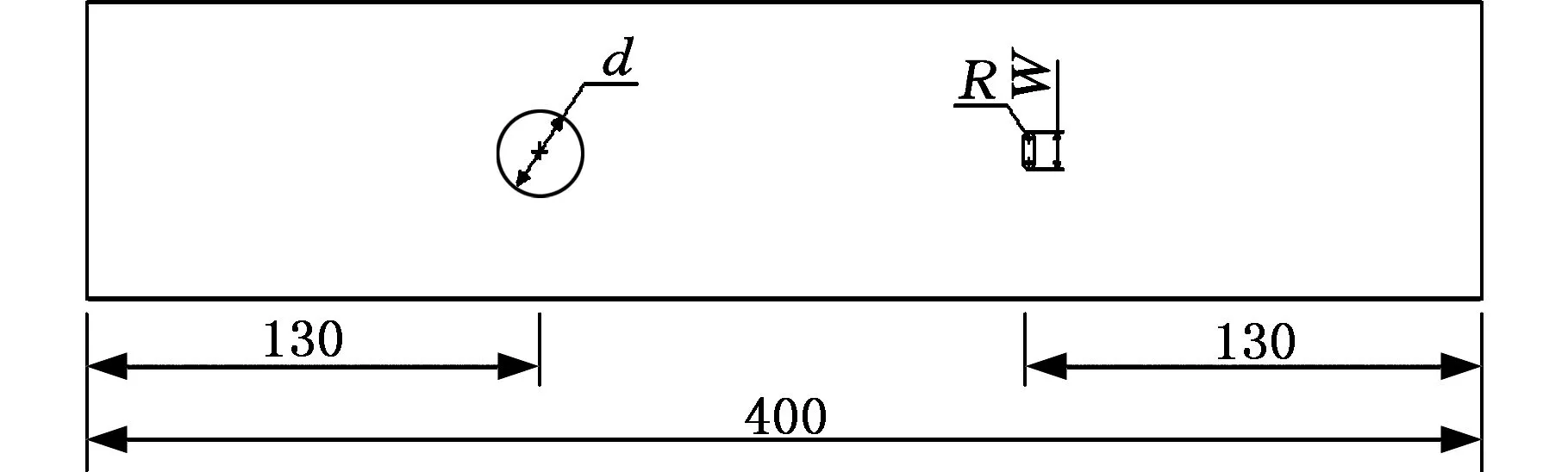
(a)DH

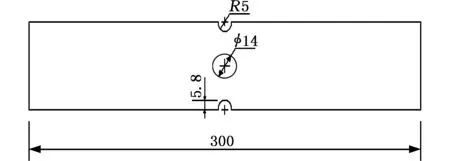
(b)DN-A

(c)DN-B图1 试件几何尺寸Fig.1 Notch geometry

从图2～图5中可以看出，球形区域内的当量应力σav与球半径r之间呈较强的线性关系。因此定义：缺口处应力梯度σsg为直线斜率k，即

表1 两种双孔试件结构尺寸
Tab.1 Dimension of two double-hole specimens

双孔试件DH-ADH-B圆孔直径d(mm)2620腰形孔长W(mm)6.59.0腰形孔半径R(mm)1.53.0

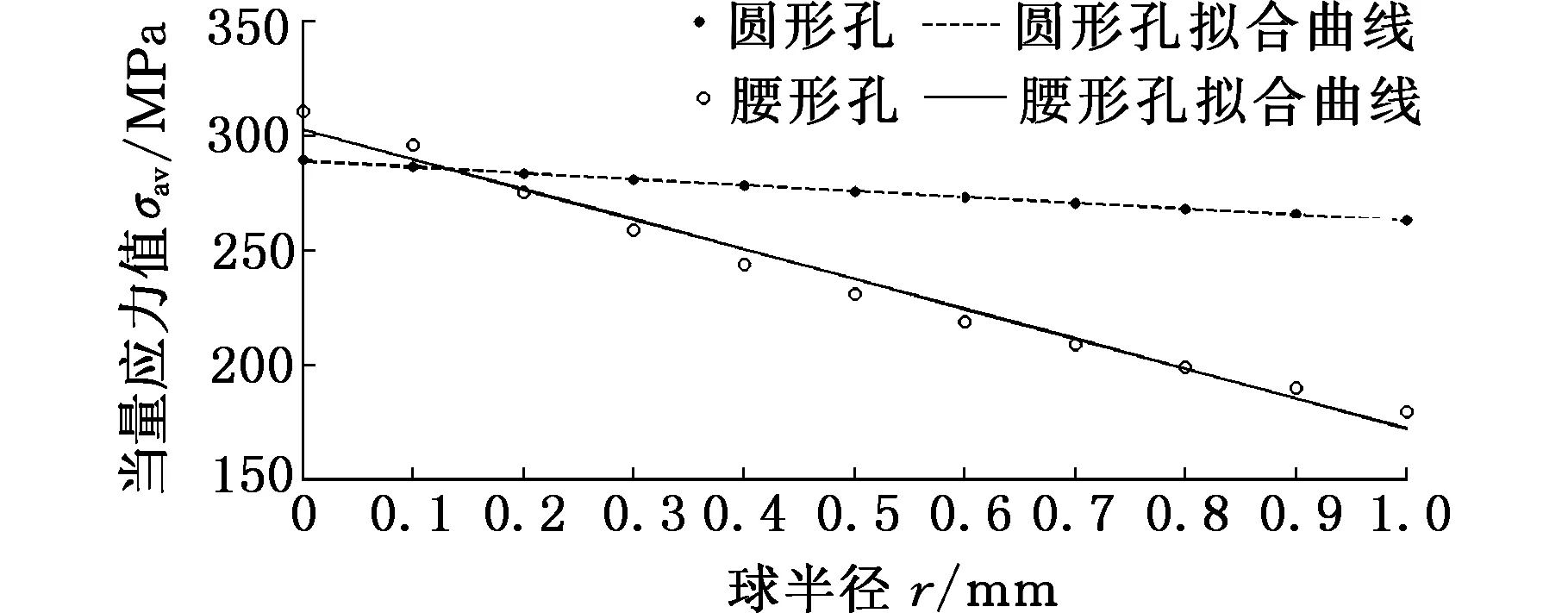
图2 当量应力值与球半径的线性表示(DH-A)Fig.2 Linear representation of equivalent stress and radius(DH-A)

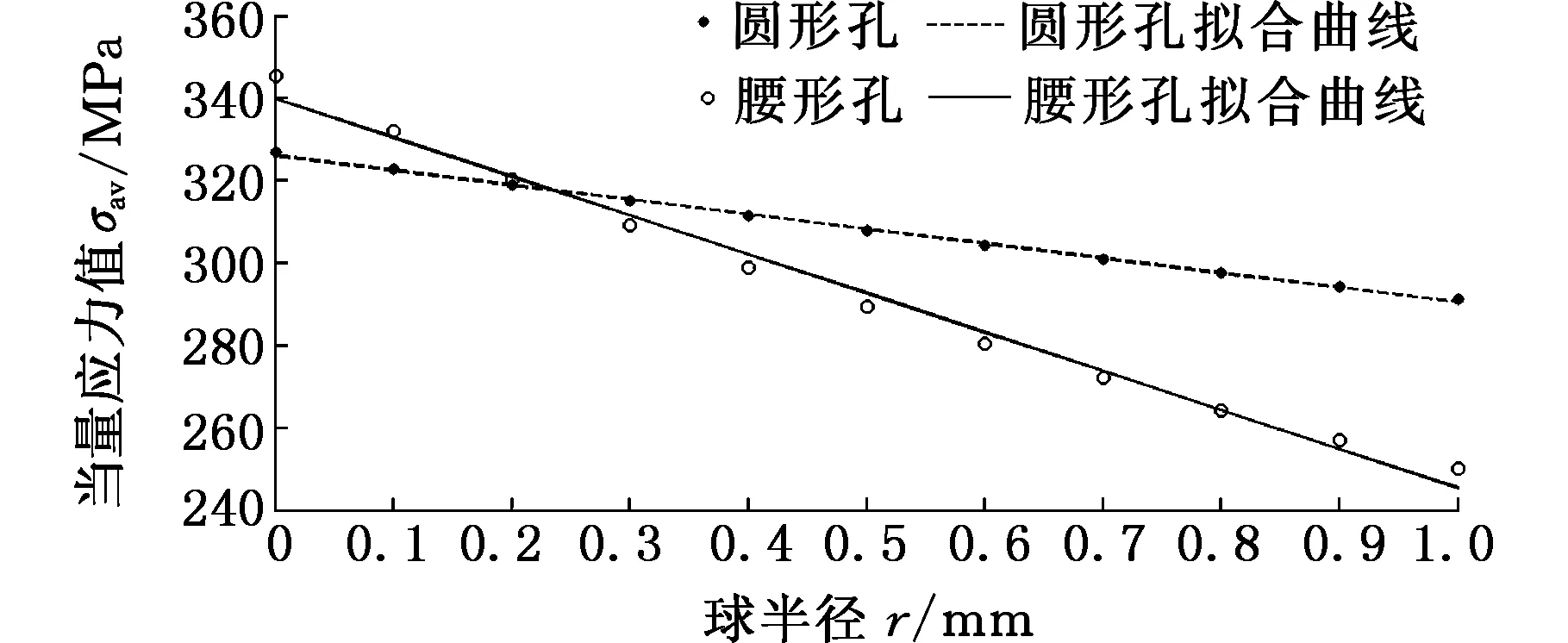
图3 当量应力值与球半径的线性表示(DH-B)Fig.3 Linear representation of equivalent stress and radius(DH-B)

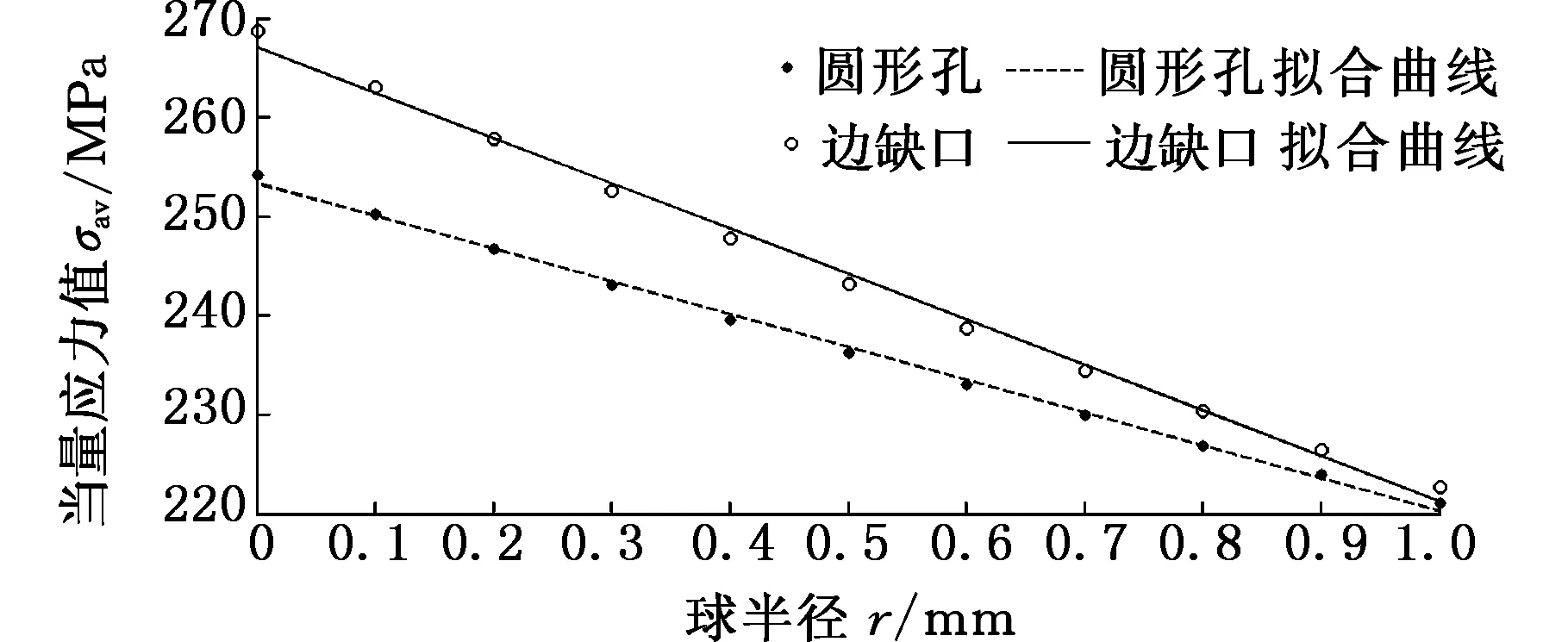
图4 当量应力值与球半径的线性表示(DN-A)Fig.4 Linear representation of equivalent stress and radius (DN-A)

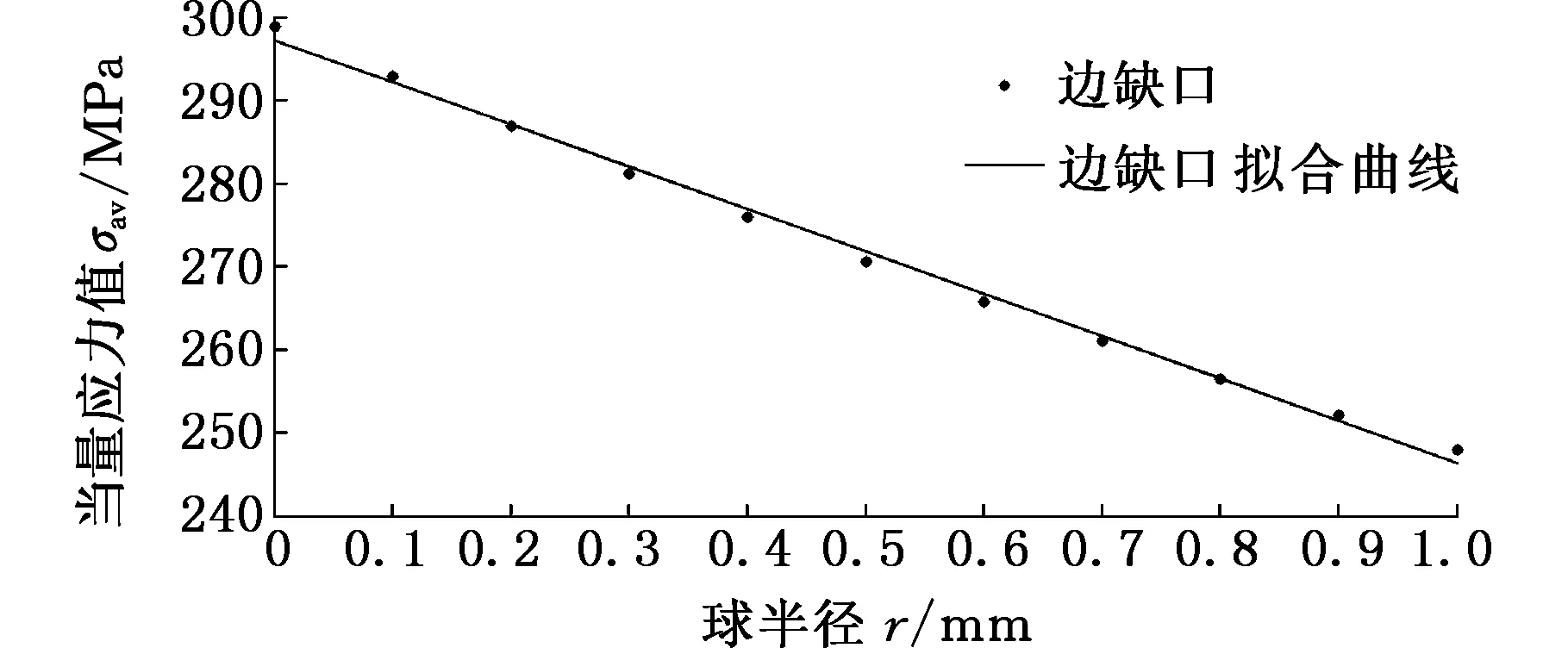
图5 当量应力值与球半径的线性表示(DN-B)Fig.5 Linear representation of equivalent stress and radius(DN-B)

定义应力梯度为缺口处当量应力下降的快慢程度；依照Siebel-Stieler[14]表示相对应力梯度χ。即

σsg=k

(2)

χ=σsg/σmax

(3)

其中,应力梯度计算结果者为负值表示σav随着r的增大而单调递减，上述试件缺口应力梯度、相对应力梯度如表2所示。

表2 缺口处应力梯度与相对应力梯度
Tab.2 Notch stress gradient and relative stress gradient

缺口最大应力值σmax(MPa)应力梯度σsg(GPa/m)相对应力梯度χDH-A腰形孔310.66-130.41-0.4198DH-A圆形孔289.23-26.06-0.0901DH-B腰形孔345.60-94.51-0.2735DH-B圆形孔326.87-35.54-0.1087DN-A边缺口268.75-45.86-0.1706DN-A圆形孔254.28-33.07-0.1301DN-B边缺口298.96-50.89-0.1702

同时试件缺口当量应力σav与球半径r的关系还可用指数函数表示，结果如表3所示。

表3 当量应力与球半径的指数表示形式

Tab.3 Exponential representation of equivalent stress and radius

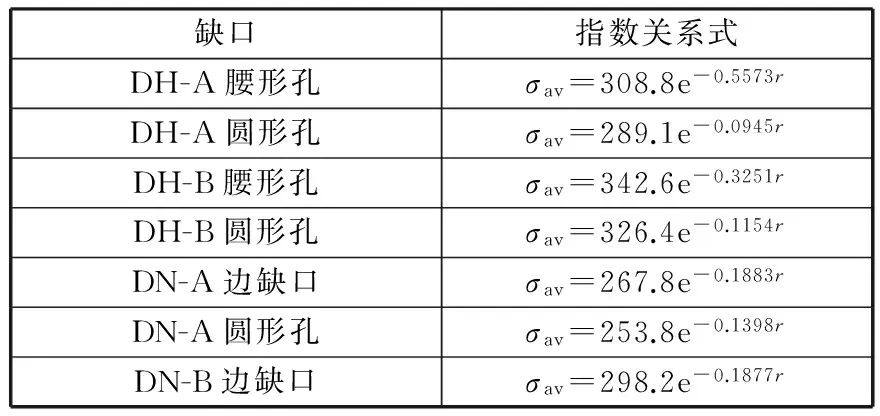
缺口指数关系式DH-A腰形孔σav=308.8e-0.5573rDH-A圆形孔σav=289.1e-0.0945rDH-B腰形孔σav=342.6e-0.3251rDH-B圆形孔σav=326.4e-0.1154rDN-A边缺口σav=267.8e-0.1883rDN-A圆形孔σav=253.8e-0.1398rDN-B边缺口σav=298.2e-0.1877r

综合当量应力值σav与r的线性和指数表示形式，代入计算结果数据，σav与r的关系可以表示为

(4)

因此结合式(1),考虑应力梯度的构件疲劳寿命数学模型为

(5)

3 球形区域半径的求取方法

3.1 球形区域半径的理论求取方法

在获得当量应力σav后，代入试件S-N曲线，即可计算当前载荷条件下的疲劳寿命预测值,因此疲劳寿命预测的准确性依赖于当量应力σav的取值是否准确。从上节σav的计算过程中可以看出，σmax、χ两个参数在构件所受载荷、约束确定后即为常数，因此当量有效应力σav取值的有效性依赖于相应载荷条件下球形区域半径r大小的确定。参照应力场强法中假设[6]，该模型假设如下：若缺口试件当量应力历程与光滑试件当量应力历程相同，则两者寿命相同。

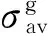
(6)

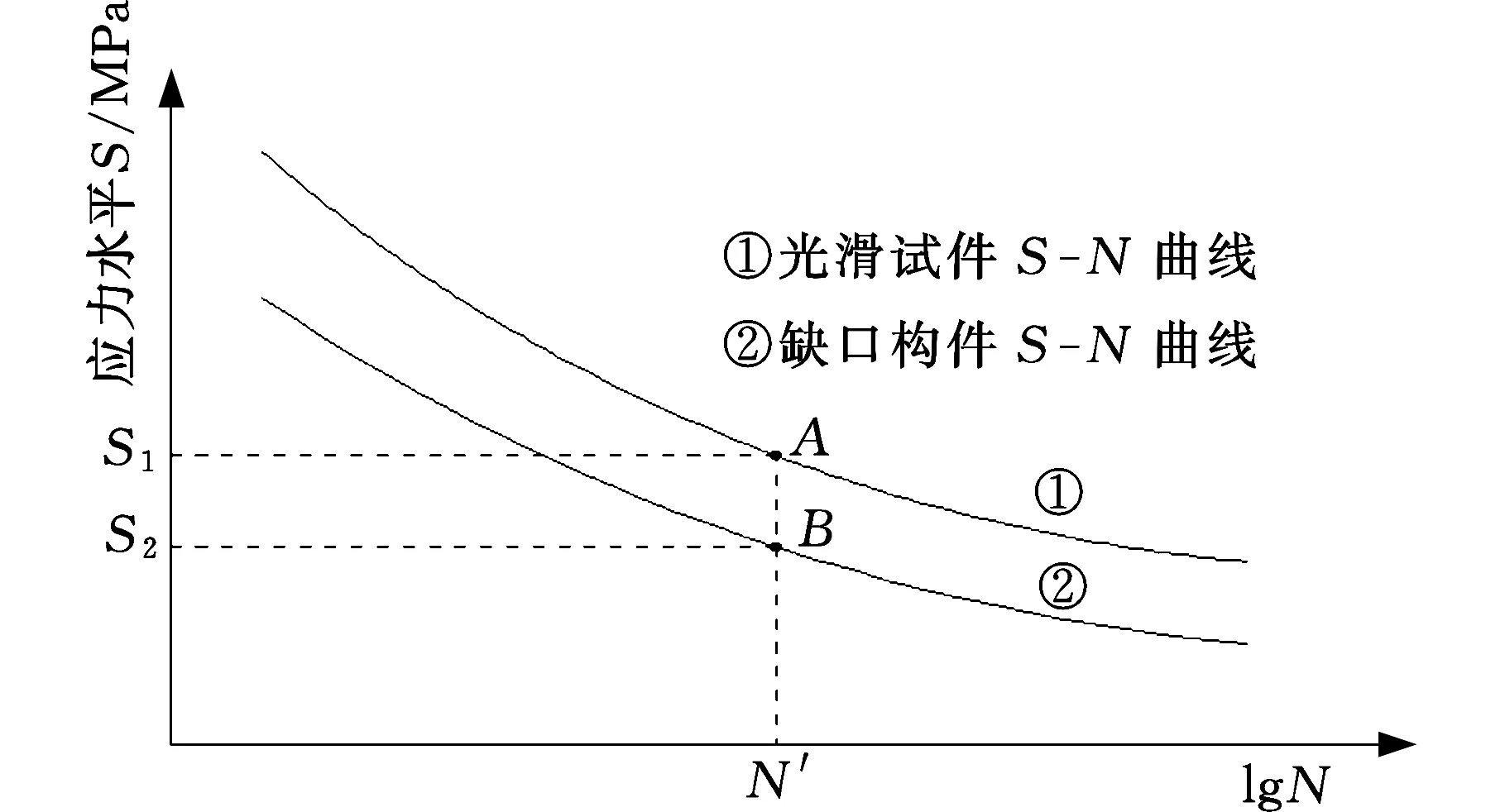
图6 光滑试件与缺口试件S-N曲线Fig.6 S-N curve of smooth specimen and notch specimen

3.2 球形区域半径的实际求取方法

由于理论求取方法在实用性上的限制，本文提出实际可操作的确定半径r的方法。取光滑试件与疲劳试件的寿命都为107，两者对应的应力水平都为其在相应载荷条件下(即不同应力集中系数、不同应力比)的疲劳极限，以两者在疲劳极限作用下的当量应力相等时的球形区域半径r来代替。实际确定r方法的操作过程如下：获取光滑试件、缺口试件在相应载荷条件下的疲劳极限，代入疲劳极限分别对光滑试件、缺口试件在ANSYS中进行应力场分析，分别取不同的r，使得结果满足式(6)，r即为所求。可采用修正的Goodman[15]或其他疲劳极限估算方法[16-17]去估算试件在不同载荷条件下的疲劳极限。无需进行试验即可获得球形区域的大小r，因此实际确定r的方法具有很强的可操作性、实用性，同时理论还可以用于应力场强法中损伤区域大小的确定。

4 算例验证

将DH-A、DH-B、DN-A、DN-B试件的疲劳试验结果用于所建模型预测精确性的验证。在第2节关于试件缺口附近应力梯度研究中，已经确定了4种试件缺口处的最大应力σmax、相对应力梯度χ，依据第3节的方法，计算上述试件缺口r的大小，代入以上数据计算当量应力σav，取得疲劳寿命预测结果，并与疲劳试验结果进行对比，结果如表4、图7所示。

表4 模型参数及预测结果值
Tab.4 Model parameters and predict results

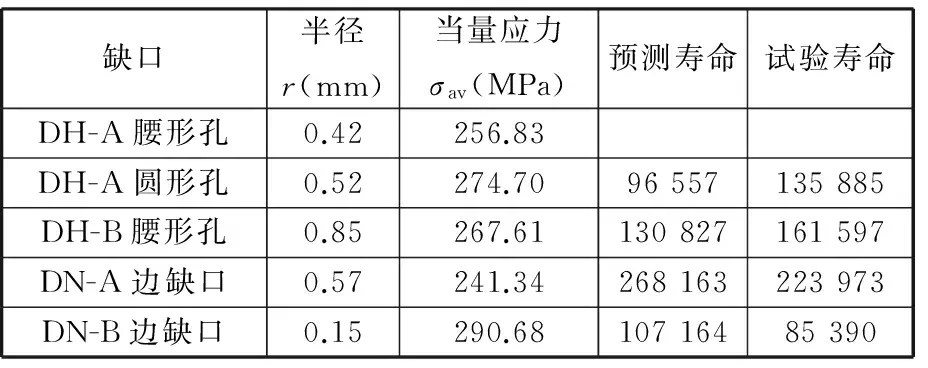
缺口半径r(mm)当量应力σav(MPa)预测寿命试验寿命DH-A腰形孔0.42256.83DH-A圆形孔0.52274.7096557135885DH-B腰形孔0.85267.61130827161597DN-A边缺口0.57241.34268163223973DN-B边缺口0.15290.6810716485390

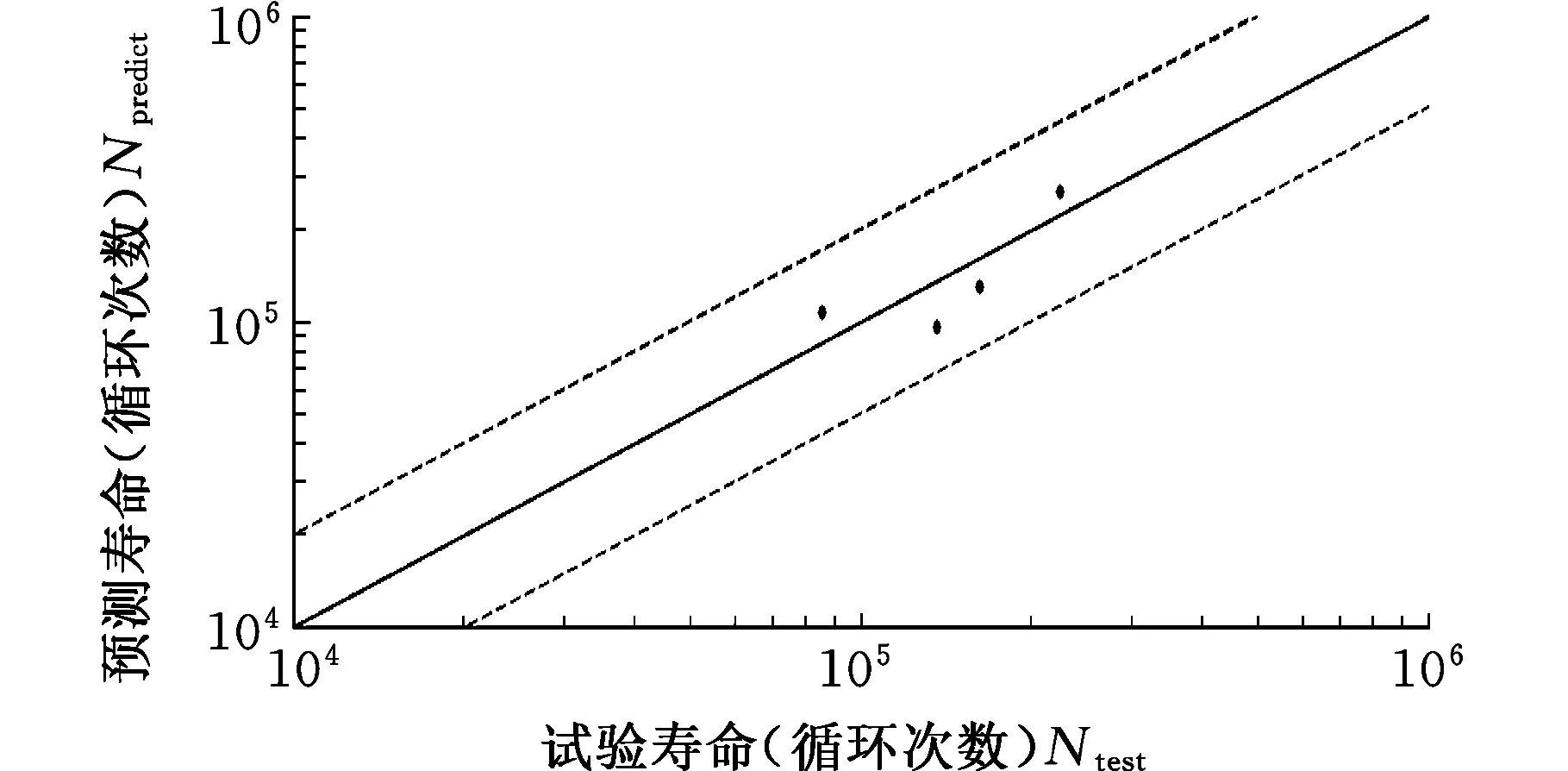
图7 模型预测寿命与试验寿命对比图Fig.7 Comparison between model predictions and test life

结果分析如下：

(1)预测结果均在2倍分散带以内(图7)，表明方法具有较好的预测精度。

(2)由表4可以看出，DH-A圆形孔当量应力大于腰形孔当量应力，由于是一板双孔，试验条件相同，理论上圆形孔较腰形孔应先发生疲劳破坏，疲劳试验结果[10-11]也表明圆形孔先发生疲劳破坏，模型准确预测了疲劳破坏位置，DH-B、DN-A同理。

5 结论

综合临界距离法计算成本小与应力场强法预测精度较高、能反映构件所处多轴应力状态的特点，构建了一种考虑应力梯度的疲劳寿命预测模型。参照一组疲劳试验对模型内参数进行了研究，用疲劳试验结果验证模型预测的准确性，得到如下结论：

(1)以缺口附近半径为r的球形区域内的等效应力均值作为控制疲劳行为的当量应力σav，σav与r之间呈较强的线性关系，同时还可用指数函数较好地表示σav与r的关系，通过定义应力梯度σsg及相对应力梯度χ，构建能够考虑应力梯度的疲劳寿命预测模型。

(2)球形区域半径r的确定方法无需进行试验，可操作性、实用性强。以光滑试件、缺口试件在相同载荷条件的各自疲劳极限作用下，两者当量应力σav相同时的r作为球形区域半径的大小。

(3)模型预测寿命均在2倍分散带内，表明方法具有较好的预测精度，同时模型可准确预测疲劳破坏位置。

[1] TANAKA K. Engineering Formulae for Fatigue Strength Reduction Due to Crack-like Notches[J]. International Journal of Fracture，1983，22(2):39-46.

[2] TAYLOR D. Geometrical Effects in Fatigue: a Unifying Theoretical Model[J]. International Journal of Fatigue ，1999，21(5):413-420.

[3] 辛朋朋，胡绪腾，宋迎东. 基于临界距离理论的TC4合金缺口试样低循环疲劳寿命预测[J].航空动力学报，2012，27(5):1105-1112. XIN Pengpeng，HU Xuteng，SONG Yingdong. LCF Life Prediction for TC4 Alloy Notched Specimens Based on Theory of Critical Distance[J]. Journal of Aerospace Power，2012，27(5):1105-1112.

[4] LANNING D B，NICHOLAS T，HARITOS G K. On the Use of Critical Distance Theories for the Prediction of the High Cycle Fatigue Limit Stress in Notched Ti-6A1-4V[J]. International Journal of Fatigue，2005，27(1):45-57.

[5] NAIK R A，LANNING D B，NICHOLAS T. A Critical Plane Gradient Approach for the Prediction of Notched HCF Life[J]. International Journal of Fatigue，2005，27(5):481-492.

[6] 姚卫星.金属材料疲劳行为的应力场强法描述[J]. 固体力学学报，1997，18(1)：38-48. YAO Weixing. Metal Material Fatigue Behavior Description of the Stress Field Intensity Method[J]. Acta Mechanica Solida Sinica，1997，18(1)：38-48.

[7] 尚德广，王大康，李明，等.随机疲劳寿命预测的局部应力应变场强法[J]. 机械工程学报，2002，38(1)：67-70. SHANG Deguang，WANG Dakang，LI Ming，et al. Random Fatigue Life Prediction of Local Stress-strain Field Intensity Method[J]. Chinese Journal of Mechanical Engineering，2002，38(1)：67-70.

[8] 郭平，陈波华，都昌兵.基于场强法的燃烧室机匣安装座疲劳寿命预测[J]. 航空发动机，2011，37(6)：36-39. GUO Ping，CHEN Bohua，DU Changbing. Based on the Approach of Field Intensity Combustion Chamber for Bushing after Installation of the Fatigue Life Prediction[J]. Journal of Aircraft Engine，2011，37(06):36-39.

[9] 张成成，姚卫星. 典型缺口件疲劳寿命分析方法 [J]. 航空动力学报，2013，28(6)：1223-1230. ZHANG Chengcheng，YAO Weixing. Typical Fatigue Life Analysis Approaches for Notched Components[J]. Journal of Aerospace Power，2013，28(6):1223-1230.

[10] 姚卫星. 结构疲劳寿命分析[M]. 北京:国防工业出版社，2003. YAO Weixing. Fatigue Life Prediction of Structure[M]. Beijing: National Defence Industry Press,2003.

[11] COLLINS J A. Failure of materials in Mechanical Design：Analysis，Prediction，and Prevention[M]. 2nd ed. New York: Wiley Publication,1993.

[12] NEUBER H. Theory of Notch Stress, Principles for Exact Calculation of Strength with Reference to structural Form and Material[M].2nd ed. Berlin:Springer Verlag,1958.

[13] 高镇同. 航空金属材料疲劳性能手册[M].北京：北京航空材料研究所，1981. GAO Zhentong. Air Metal Material Fatigue Performance Handbook[M]. Beijing: Beijing Institute of Aeronautical Materials,1981.

[14] SIEBEL E，STIELER M. Significance of Dissimilar Stress Distributions for Cycling Loading[J]. VDI-Z，1955，97(5):121-126.

[15] 项彬，史建平，郭灵彦，等. 铁路常用材料Goodman疲劳极限图的绘制与应用[J]. 中国铁道科学，2002，23(4):72-76. XIANG Bin，SHI Jianping，GUO Lingyan，et al. Plotting and Application of Goodman Fatigue Limit Diagram of Railway Common Materials[J]. China Railway Science，2002，23(4):72-76.

[16] 李舜酩.机械疲劳与可靠性设计[M]. 北京：科学出版社，2006. LI Shunming. Mechanical Fatigue and Reliability Design[M]. Beijing: Science Press,2006.

[17] 李海梅，宋刚，刘勇志.金属材料疲劳极限的估算[J].郑州大学学报:工学版，2002，23(4): 26-29,39. LI Haimei，SONG Gang，LIU Yongzhi. Estimating Formula of Fatigue Limits for Metallic Materials[J]. Journal of Zhengzhou University: Engineering Science Edition，2002，23(4): 26-29，39.

(编辑 袁兴玲)

Predicting Method for Fatigue Life with Stress Gradient

SHEN Jiebin TANG Donglin

School of Mechanical and Electrical Engineering of Southwest Petroleum University，Chengdu，610500

Aiming at the problems that existed in the predicting the fatigue life processes by the critical distance method and the stress field intensity method, taking advantages of the two methods, an equivalent stress approach was proposed, where the effective stress average in spherical regions near the notch was taken as fatigue behavior control parameters. According to a set of fatigue tests, the relationship between the equivalent stress and spherical radius was studied, results show the relationship is well represented in the form of linear and exponential functions, by defining the stress gradient and relative stress gradient, a fatigue life prediction model was constructed considering the stress gradient. Determination of parameters in the model was studied, The spherical radius with the same equivalent stress of the smooth specimen and the notched specimen was taken as the damage region size under action of fatigue limit in the same load condition. The spherical radius was obtained without test, so this method had a strong practicality. Validation of the fatigue test results indicates that the model prediction results are within 2 fold of the dispersion bands, show that the model has good prediction accuracy; the model may also predict the fatigue damage location.

notch；stress gradient；stress distribution；fatigue life prediction

O346.2

10.3969/j.issn.1004-132X.2017.01.007

0 引言

2015-10-12

2016-11-15

申杰斌，男，1991年生。西南石油大学机电工程学院硕士研究生。主要研究方向为石油装备疲劳可靠性。E-mail:2081703017@qq.com。唐东林，男，1970年生。西南石油大学机电工程学院教授。

由于缺口引起的结构不连续特征会导致结构