压电膜片式微喷的多场耦合仿真模型及其应用

王 堃 习俊通,2

1.上海交通大学机械与动力工程学院，上海，2002402.机械系统与振动国家重点实验室，上海，200240

压电膜片式微喷的多场耦合仿真模型及其应用

王 堃1习俊通1,2

1.上海交通大学机械与动力工程学院，上海，2002402.机械系统与振动国家重点实验室，上海，200240

基于自行设计制造的压电驱动膜片式微喷装置的实际结构，建立了一个多场耦合的数值模型，用来研究压电驱动的膜片式微滴喷射过程中的参数作用和变化规律。在模型的建立过程中，对流体部分的湍流判定和表面力作用的关键技术问题进行了分析研究。该模型能较好地模拟微喷装置工作过程。利用该模型研究了驱动波形对液滴属性的决定关系，以及液体腔中一个工作周期内压力的变化规律等问题。

压电驱动；膜片式微喷装置；数值模拟；按需喷射

0 引言

压电驱动的微滴喷射技术是一种数字化控制微米级液滴产生和分配的技术。由于具有精确控制、高效率、高材料利用率等优点，故基于微滴喷射技术的加工制造工艺在生物医药实验、微电子封装、MEMS、微光学元器件制作等领域展现出巨大的应用潜力。为了使压电微喷装置的设计和应用更加高效，必须掌握其各种参数的影响规律。除了进行实际的物理实验研究之外，基于计算机数值仿真模型的分析也是一种有效且可靠的研究方法，国内外许多学者在此方面做了大量工作。CHEN 等[1]建立了一个理想化的压电驱动微喷装置的流体数值模型，并利用该模型研究了液滴形成条件、液滴体积和速度与外加驱动的关系、液滴体积与液体腔体积变化的关系等问题，阐明了压电驱动微喷装置液滴形成过程的一些基本规律。KIM 等[2]建立了一个基于真实装置尺寸的流体模型，利用高性能工作站仿真了压电驱动微喷装置的液滴喷射过程，研究了驱动电压和液体属性对喷射结果的影响规律。SACHS 等[3]针对喷射出的液滴在空气中的飞行过程建立了流体控制方程，从而优化液滴的飞行稳定性，保证液滴落在基板上的位置准确，提高三维打印的精度。

然而目前可见的研究基本都是针对微喷装置的流体部分建立数值模型，而微喷系统是一个结构、流体以及压电、热等多物理场高度耦合的系统，仅有流体模型难以反映其全貌，也无法直接体现结构等参数对喷射的影响。本文提出了一个流固耦合的微喷装置数值模型，该模型可以直接实现从压电驱动导致的结构变化到最终喷射液滴形成并落在基板上的全过程，无需通过假设和间接转换等方式来体现结构或驱动参数的变化，从而能够更方便和准确地研究微喷过程中的各种规律。

1 流固耦合微喷数值模型的建立

1.1 多场耦合模型相对于纯流体场的优势

压电驱动的微喷装置的驱动能量是通过“压电—结构—流体”的顺序传递的，而流体获得动力形成液滴后，又会对结构部分产生反作用，因此整个装置是一个多物理场高度耦合的系统。流固耦合的数值模型能够真实接近这个物理过程，给分析人员提供一个接近黑箱的系统——物理过程与仿真过程的输入参数一一对应，而非将结构部分的输入通过计算转换成流体的边界条件来模拟参数变化。如压电驱动器的驱动电压波形，就可以在结构分析模块中直接输入真实值，而对于纯流体模型，就只能采用流体入口的流速或压力变化来近似这种外加驱动。

此外，在纯流体模型中，由于入口的边界条件只能设定为流体的流速压力等，而这些条件是由多个参数共同计算或近似得出的，故仅通过流体的边界条件设定，难以反映多个输入参数分别作用效果，也无法反映一些复杂的输入参数(如不规则的驱动波形)。同时，对于一些温度变化作用显著的情况——如液体温度较高或液体的性能参数随温度变化较大时，流固耦合的数值模型中加入温度场的分析非常方便。另外，流体对固体结构的反作用在微喷这种尺度较小的结构中也是不能忽略的，只有流固耦合模型才能将这种反作用纳入计算之中。

1.2 多场耦合模型的系统结构

本文采用的多场耦合模型是双向耦合结构，即在每一步都传递数据，流体计算传递的数据为压力，固体求解器所传递的数据为节点位移。这样在每一次迭代后更新固体载荷与流场情况。具体的系统结构如图1所示。

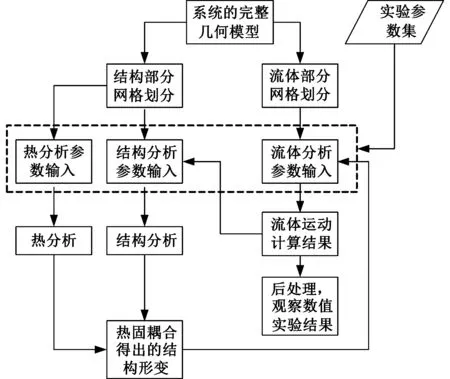
图1 多场耦合模型的系统结构Fig.1 Structure of the multi-field coupling model

1.3 建模的理论和算法

本模型的控制方程是流体连续性方程和Navier-Stokes方程，这是几乎所有计算流体力学问题的基础。

流体部分的计算方法采用有限体积法。而对于多相流问题的处理，则应用VOF(volume of fluid)方法，通过研究网格单元中流体和网格体积比函数来确定自由面，追踪流体的变化，而非追踪自由液面上质点的运动。定义液体体积分数φ=φlρ/ρl，其中，φl表示接触面上某点的液体质量分数，ρl表示液体密度，ρ表示气液混合流体平均密度。φ的取值为：当单元全部为液体时，φ=1；当单元全部为气体时，φ=0；当单元为液体气体混合时，0<φ<1。而各相流体浓度守恒的控制方程为

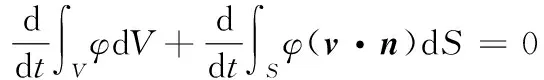
在接触面单元上，两种流体分别考虑其单独作用，而各单元内混合流体的物理性质取决于单元内各流体的体积分数。密度和黏度用线性插值的方法计算，具有相同的形式，即φ=aφl+(1-a)φg，其中下标表示各单元内混合的两种液体。

本模型中对于流体部分气-液两相流的处理采用了单一计算域的方法，同时采用了以位置为参数的初始状态体积分数函数，实现对不同相流体的定义。相对于将每一相液体定义成一个计算域的方法，单一计算域避免了界面处的网格不连续和流体进出容易导致的计算不收敛问题，计算更精确高效。

1.4 模型建立及其初始状态定义

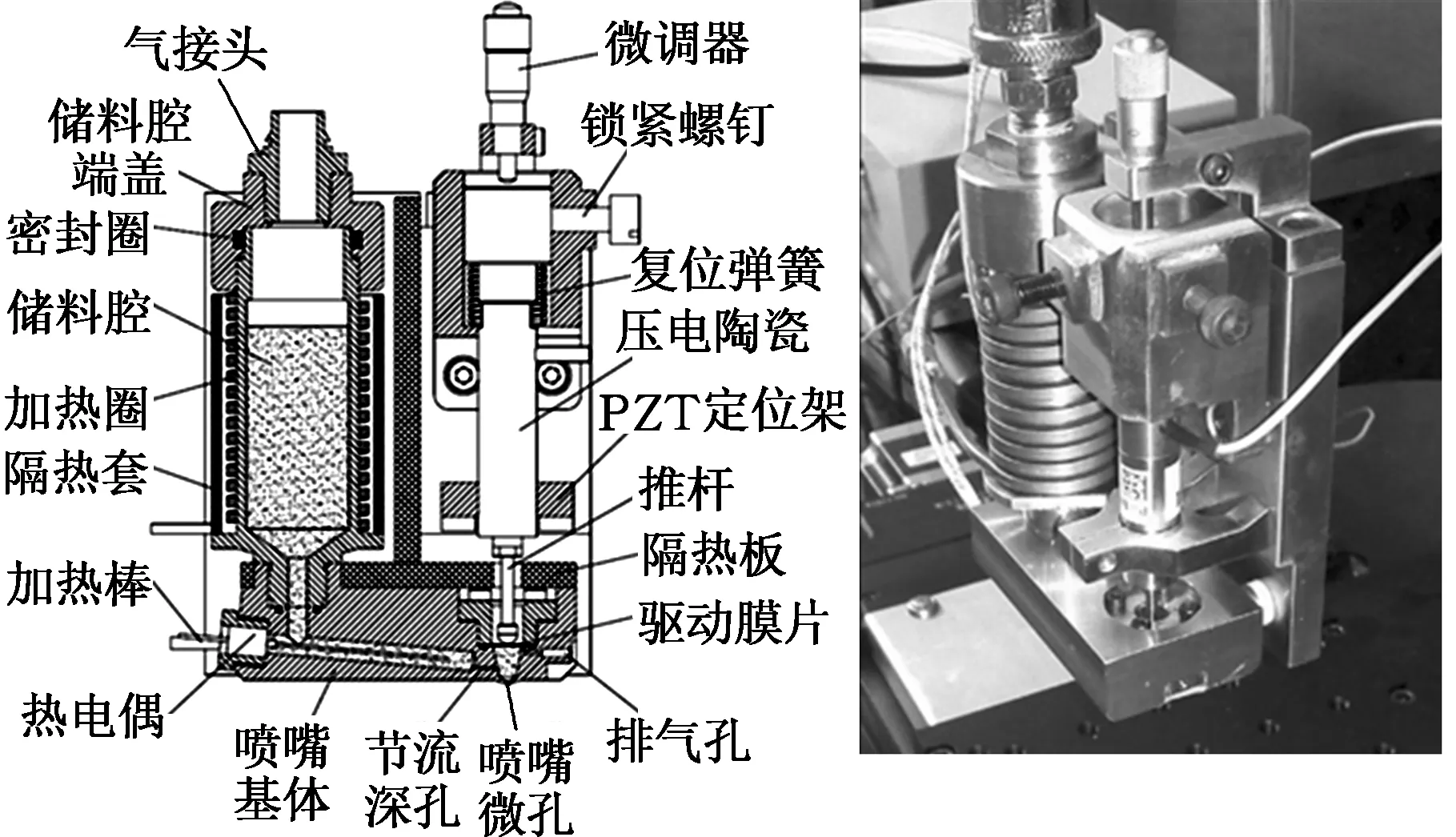
图2 压电驱动膜片式微喷装置Fig.2 Piezoelectric actuated diaphragm-driven microjet printhead

本模型基于笔者实验室自行研制的实验装置的实际尺寸建立[4]，装置如图2所示。这一装置可用于电子封装中的点胶工艺，也可在选择适当材料后用于3D打印。装置安装于伺服电机驱动的三轴平移台架上。所采用的压电驱动器为PI公司出品的P-841型，其压电材料为PIC255，其驱动行程为15～90 μm，推力最高可达1 kN，空载振动频率为6～14 kHz。振动膜片选择了304不锈钢材质，直径4.5 mm，厚度0.2 mm。

本文中，将实验装置的喷嘴附近局部结构提取出来建立流固耦合数值模型。图3所示是隐藏了流体部分并计算完振动膜形变量的固体部分的截面，固体部分的变形量会直接传递给与其接触的流体部分，作为流体部分的初始条件。压电驱动器作用于振动膜中心点上侧，驱动器形变的距离和速度也就是该点竖直方向的形变情况。图4所示是包含隐藏的固体部分轮廓的流体部分初始状态。上方深色部分为微喷装置液体腔中充满的待喷射液体，下方浅色部分为液滴喷出后将要飞过的一段空气柱。

图3 计算了振动膜形变量的固体部分Fig.3 The solid part with calculation of vibration film deformation

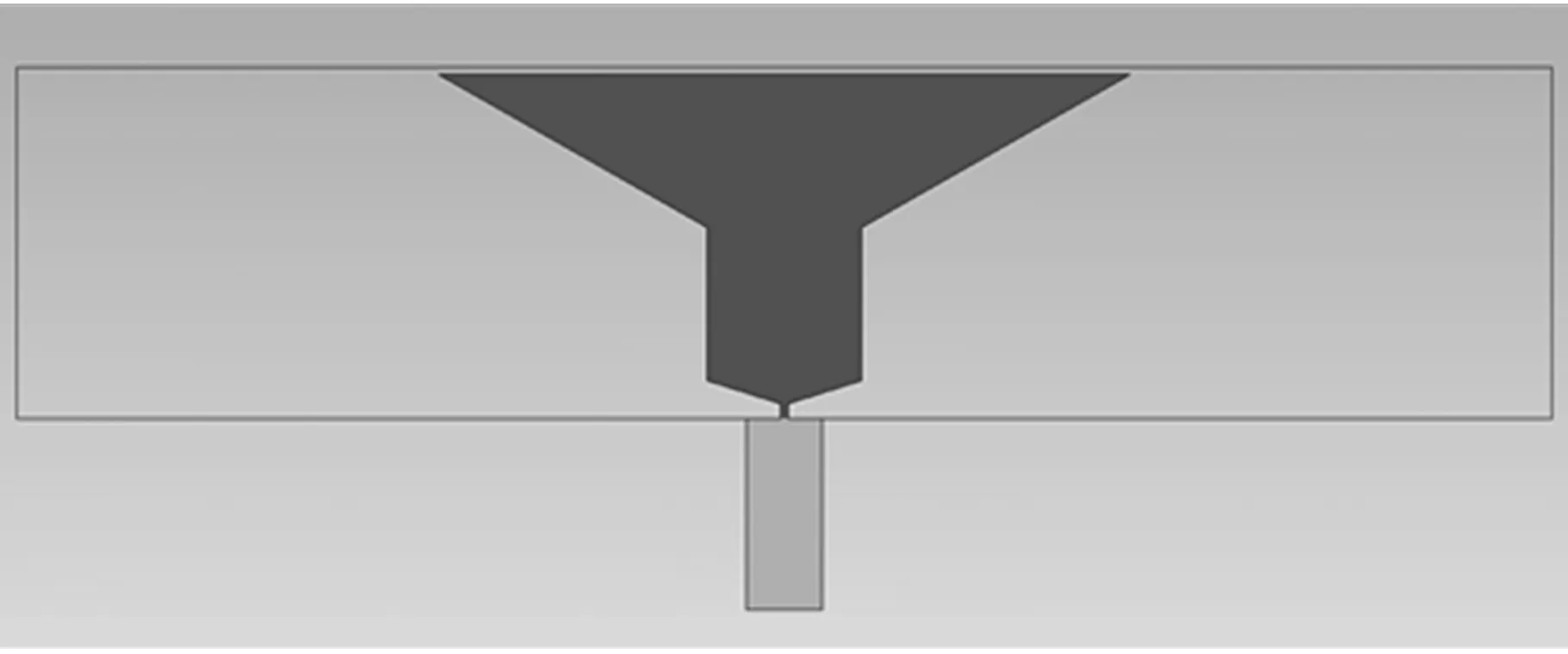
图4 流体部分的初始状态Fig.4 Initial state of the fluid part

1.5 微喷数值模型中流体的层流和湍流判定

流体力学计算中，湍流的处理是非常重要的内容。目前能用于工程计算的处理湍流数值计算的方法(如κ-ε两方程方法等)都属于雷诺平均N-S方程(RANS)方法[5]。其思路是:首先将满足动力学方程的湍流瞬时运动分解为平均运动和脉动运动两部分，平均运动部分用N-S方程表示;然后把脉动运动部分对平均运动的贡献通过雷诺应力项来模块化，也就是通过湍流模式来封闭雷诺平均N-S方程使之可以求解[5-6]。对于微喷这样的尺度微小从而具有很小的特征直径D的情形，如果能够判定流体处于层流状态，那么在计算时便无需附加湍流模式，从而显著提高计算速度和稳定性，而减少湍流方程中的不确定变量也能提高计算结果的精确度。因此在建立此数值模型时，对于其是层流或是湍流的判定是非常必要的，会决定流体计算中采用的算法和设定。

湍流和层流的判断通常以流体的雷诺数Re=Dv/ν为准[7]，其中，v表示流体的特征速度，ν表示流体黏度。对于微喷装置这样的不规则流道，很难直接估测其特征直径和特征速度，考虑到计算流体力学中对湍流的处理采用附加湍流模式的方法，本文用以下步骤来考察整个流场的层流或湍流状态：

(1)对整个流场采用湍流模型进行计算。根据前述的湍流计算方法，即使流体处于层流状态，附加的湍流模式也不会显著影响计算结果(即在层流状态下，湍流模式对平均运动部分的贡献方式与湍流状态相同，但影响小到可以忽略不计)；

(2)记录计算过程中每一步得到的流体各部分的雷诺数。雷诺数作为计算流体力学方法算出的结果之一，在每一计算单元的每一迭代步骤中都可以输出；

(3)观察所有雷诺数，综合评估流体在整个计算过程中的状态。

在建模过程中，分别采用该微喷装置常用的两种典型工作液体——水和甘油，驱动参数设置为常用值，针对本例中的适用情况采用了剪切压力传输(shear stress transport, SST)方法进行计算，观察到各计算单元的全过程雷诺数最大值分别为37和21。虽然具体数值随着模型中任何一个参数的改变都会发生变化，但就其数量级而言，即使考虑计算误差和实验假定等因素，该数值也远离湍流区间。因此可以认为，对于微喷装置这样的尺度和黏性相对较高的液体，其全过程都可以采用层流模型进行计算。这个结论也与一些文献中对细小流道采用直接估算的方法得出的结果相一致[8-9]。

1.6 流场中的表面力效应

液体与固体之间的界面力、浸润、亲水性和疏水性等，在宏观尺度流动中往往是可以忽略的物理因素，然而在微喷装置的微小尺度下，表面积相对体积的增大，使表面力影响增强，同时流场空间尺寸的缩小，也突出了这些界面[8，10]。以壁面的浸润性为例，在大多数目前可见的数值仿真研究中，对于微喷装置喷嘴附近液体与壁面的浸润性都参照宏观流动的参数设置将其接触角设置为90°，即壁面无任何作用。然而在这样的微小尺度流动中，表面积相对增大使得表面力影响增强，由表面张力引起的浸润性的作用是不能忽略的。

在建模过程中，笔者对喷嘴附近壁面浸润性的影响作了实验验证：固定一种常用的工作液体(水)和驱动参数不变，观察壁面接触角分别为60°(亲水)、90°、120°(疏水)时喷射液滴的体积和速度，结果如图5和图6所示。可看出当喷嘴附近壁面接触角小于90°具有亲水性时，喷射液滴体积和速度都会减小。显然这是由于亲水性使得喷嘴外的壁面有将液体吸附于其上的趋势，这会阻碍液滴的形成；而当壁面具有疏水性时则正好相反，液滴会更容易形成。

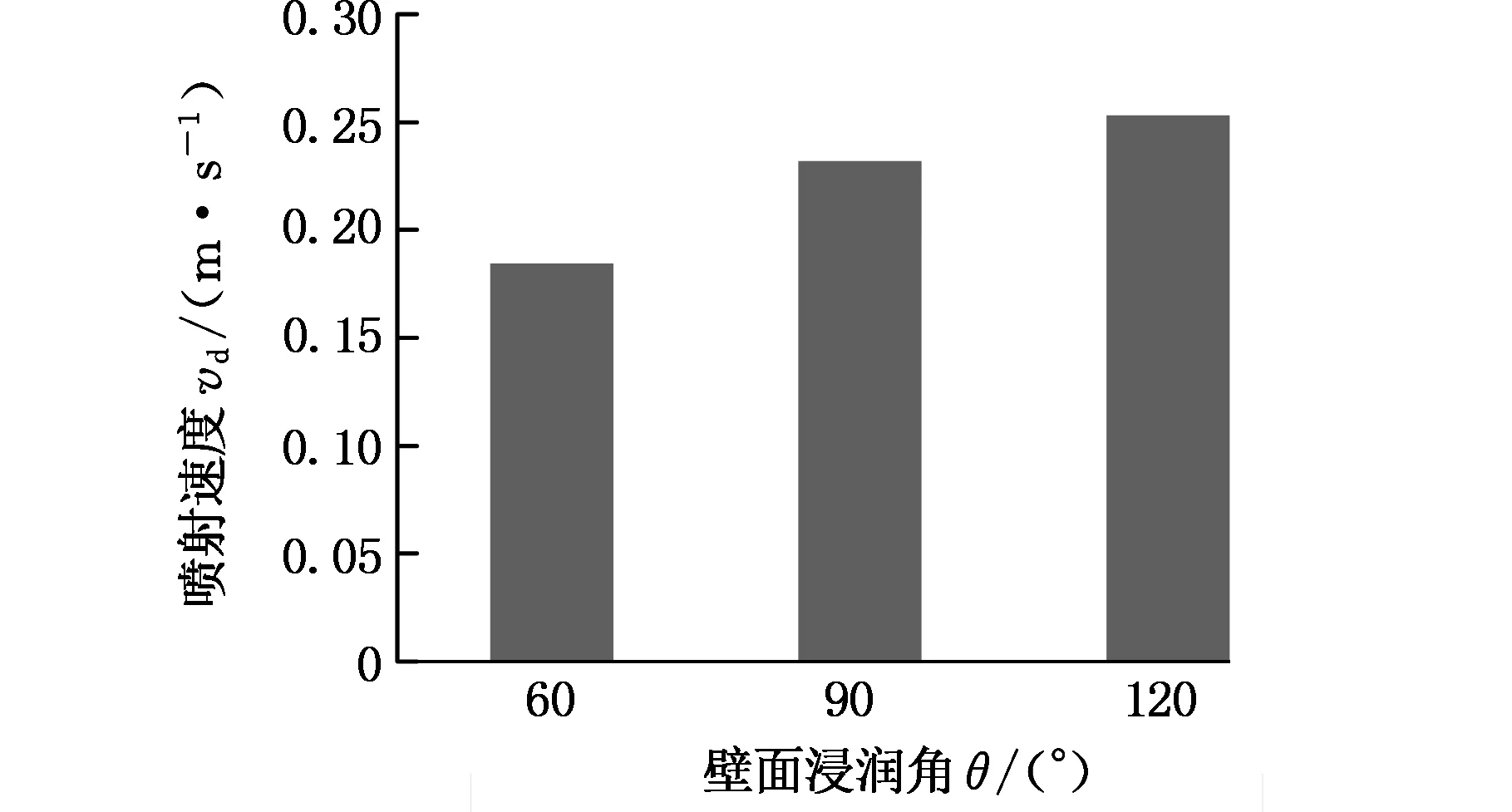
图5 壁面浸润性对喷射液滴速度的影响Fig.5 Effect of wettability on the velocity of droplets

图6 壁面浸润性对喷射液滴体积的影响Fig.6 Effect of wettability on the volume of droplets

由此可见，在建立微喷装置数值模型时，壁面的浸润性是必须要考虑的参数。在实际的实验中，壁面的浸润性会受到材料性质、边缘形状和壁面粗糙度等多种因素影响，因此针对不同情况都应先测量或估计壁面接触角，以此来设置数值模型中的参数，才能保证数值模型尽可能地接近实际状态。当根据仿真结果指导实验时，也应将喷嘴附近加工成尽量接近数值模型参数中设置的浸润状态。

2 仿真计算结果与分析

2.1 液滴喷射过程仿真

利用该流固耦合数值模型，按照实际工作状态设置驱动参数和环境条件后，便可计算出液滴喷射结果。在计算结果中，利用单元中液体的体积分数云图可直观看出液滴形状，在此将阀值设定为70%，即当一个微单元中液体的体积分数高于70%时，便认为这个单元全部由液体组成，否则认为是气体。

该喷射过程的驱动波形上升阶段为0～0.5 ms。从图7中可看出液滴形成过程：在驱动波形上升阶段，液体持续被挤出；当波形上升阶段结束，挤出的液体由于惯性继续前进，而液体腔内的液体停止运动，从而在喷嘴附近产生颈缩现象；当t=0.9 ms附近时，颈缩达到极端而彻底断裂，喷出液体与液体腔分离形成独立液滴向基板飞行。适当的驱动器形变速度和形变距离是形成稳定液滴的必要条件。如果驱动不足，液体挤出后会因无法克服其表面张力而断裂，会随着驱动器回位而回到喷嘴内；如果驱动过度，则液体喷出过多，断裂后会形成多个液滴甚至形成连续的液柱，不能满足工作要求。

图7 喷射液滴过程Fig.7 Droplet injection process

在图8中展示了液滴飞行结束落在基板上的情景。在此次仿真中采用了一个完全自由滑动的基板，可以看到液体逐渐落在基板上向四周扩散并产生一定幅度振荡的过程。将基板与液体的接触性质根据不同的实际情况进行设置，就可以预测分析喷射最终形成的液滴形状等信息。

图8 液滴着陆于完全自由滑动基板上的过程Fig.8 Process of droplet landing on the free-slip base plate

2.2 驱动参数对液滴的影响分析

对微滴喷射来说，液滴的喷射速度和体积是最重要的两个性能指标。本文利用微喷装置流固耦合的数值模型，研究了压电驱动的驱动器形变速度和形变距离对液滴指标的影响，这两个参数可直接通过输入电压波形来调节。在这些研究中，装置的几何尺寸保持不变，工作液体均设定为常温下的纯水。

(1)驱动参数对液滴喷射速度的影响。在固定另一参数的情况下，驱动器形变速度和形变距离对液滴喷射速度的影响曲线分别见图9和图10。从图9和图10中可看出：在测试范围内，液滴喷射速度随着驱动器形变速度的增大基本上呈线性增长；而形变速度不变的情况下，喷射速度基本不随形变距离发生变化。

图9 驱动器形变速度与液滴喷射速度的关系Fig.9 Relation between the driver deforming speed and droplet jetting velocity

图10 驱动器形变距离与液滴喷射速度的关系Fig.10 Relation between the driver deforming length and droplet jetting velocity

(2)驱动参数对液滴体积的影响。驱动器形变速度和形变距离对液滴体积的影响曲线分别见图11和图12。从图11和图12中可看出：在测试范围内，当驱动器形变距离不变时，液滴体积基本不随形变速度的变化而改变；同时，随着驱动器形变距离的增长，液滴体积也呈相应增大状态。

图11 驱动器形变速度与液滴体积的关系Fig.11 Relation between the driver deforming speed and droplet volume

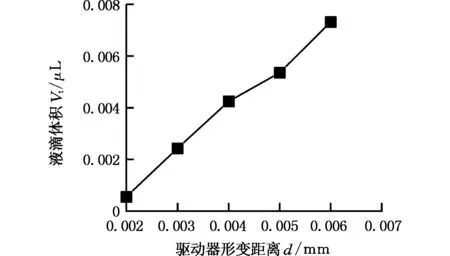
图12 驱动器形变距离与液滴体积的关系Fig.12 Relation between the driver deforming length and droplet volume

总之，由以上分析结果可得，对于压电驱动的膜片式微喷装置的驱动参数，液滴的喷射速度主要由驱动器形变速度决定，而液滴体积主要由驱动器形变距离决定。在该装置之前进行过的实验研究中曾有过结论：驱动频率的增大将导致压电驱动器形变距离的减小，从而使液滴体积减小。这一结论中的变化趋势与流固耦合模型得到的计算结果一致，也证明了该数值模型的可靠性[11]。

2.3 喷射过程中液体腔内压力的变化

为了研究压电驱动微喷装置工作过程中液体腔内部的压力变化情况，在装置中心线上液体腔内部取一系列参考点，分别命名为Point05～Point35，如图13所示。命名中Point后面的数字表示该点在竖直方向距喷嘴初始气液界面的距离，Point05表示距离为0.5 mm，依此类推。分别读取各点在整个周期中的相对压力(相对于外界环境压力)。

图13 观察液体腔中压力变化的参考点Fig.13 Reference points for observing the pressure in the fluid chamber

图14所示为在梯形驱动波形作用下，液体腔内各参考点在一个周期内压力的变化情况。可见当振动膜在压电驱动器作用下变形，液体受到作用后压力并非均匀增大或减小，而是呈现一个振荡过程。结合对照的驱动波形，振动膜变形和恢复分别造成一次方向相反的冲击，引起液体振荡；冲击结束后，振荡逐渐衰减。从图14中可以看出两个问题。

图14 液体腔内各参考点压力随时间的变化Fig.14 Time series of the reference points pressure

(1)图14中波形正负两个极值附近区域a和b放大，如图15所示，图15a中显示出各参考点压力达到正值极值的时间是随着到喷嘴的距离减小而依次延迟的；而从图15b中则可看出压力达到负值极值的顺序恰好相反。这反映出了液体腔内部随时间变化的情况：当振动膜变形后，靠近振动膜部分的液体压力增大，产生一个波峰逐渐向喷嘴方向传递，从而形成了各参考点压力正值的极值，这个压力变化也是喷嘴处挤出液体的直接原因；当振动传递到喷嘴附近壁面时并没有消失，而是被壁面反射回来，使得各参考点压力经历了一次反向变化，形成了负值的极值；之后液体腔内部的振动逐渐衰减；在振动膜恢复平衡状态时，对

(a)图14中a处放大 (b)图14中b处放大图15 压力波形的两个峰值局部放大Fig.15 Detail of the local area of the two peaks of the pressure wave

液体腔形成一个反向的冲击，从而液体腔内部再次经历了一个振幅小很多的反向衰减振动过程。

(2)图14中显示的液体腔内部压力变化体现的是微喷装置对于脉冲驱动的响应特性。观察波形可见，这个响应与带阻尼的二阶系统响应非常相似。实际上，KIM等[12]认为压电驱动膜片式微喷装置是一个二阶响应系统，并利用实验装置测定了膜片对脉冲驱动的响应曲线。微喷装置内部的压力本身难于直接测量，膜片的振动情况可以在一定程度上反映实际的压力变化。比较文献[12]中膜片振动曲线，可以看出膜片振动曲线与本文中的数值模型得到的响应曲线特性非常相似。

对于按需喷射的压电膜片微喷装置，在液滴形成后，液体腔内的持续振荡是有害于其工作性能的，故每次喷射结束后必须等待振荡基本恢复零点之后才能进行下一个周期的工作，以保证连续喷射的一致性。这种振荡也是产生卫星滴的直接原因[13]。而基于微喷装置是一个二阶响应系统的设定，KIM等[12]和KHALATE 等[13]利用实验装置进行了通过控制驱动波形来减小和抵消多余振荡，缩短整个系统恢复零点所需时间的研究，这对于提高微喷装置性能非常重要。本文中的数值模型响应特性与实验装置一致，说明该模型可以一定程度上替代实验装置来进一步进行这方面的相关研究。

2.4 气泡对于连续喷射的影响

在实际使用中，微喷装置都是连续高频循环工作的。在利用数值模型对其多个周期进行连续仿真时，发现第一周期振动膜恢复平衡状态时吸入的空气会在喷口附近形成气泡(图16)，导致第二次喷射无法完成。即使第二个液滴能够喷出，其性质也会与第一个液滴有较大差别。这个现象说明了液体腔中的气泡是微喷装置必须考虑的一个重要因素，解决其对喷射稳定性的干扰可以采用以下办法：

(1)在微喷装置的进料口增加气压设备，使液体腔内始终处于高压状态。此时气泡刚一形成便会立刻被液体填充，保证了下次喷射的良好初始状态。本文中的装置在实际实验中便采用了这一方法，效果良好。但这一方法的缺陷是附加了很多复杂设备，高压的气动管路也降低了整个实验系统的可靠性。

(2)在驱动波形的两次喷射之间，设置一定长度的“空载”间隔。在此过程中，整个装置无任何动作，等待气泡在浮力的作用下自行脱离喷口，液体填充空腔。这种方法实现简单，但牺牲了微喷装置的工作频率，每次喷射之间的“空载”间隔数倍于驱动器工作时长，效率较低。

图16 第二个喷射周期开始时喷口附近的气泡Fig.16 Bubble around the nozzle in the beginning of the second jetting period

如果要利用数值模型准确研究气泡的作用规律，必须在流体分析中包含浮力计算，这在目前的研究中大都是忽略的。包含浮力的流体分析会延长计算时间，并显著降低计算稳定性，但对于连续多个周期的喷射过程仿真来说是必须的，在研究中应根据研究对象的实际情况和研究目的来进行取舍。

3 结论

(1)包含流体和固体等的多场耦合的数值模型能够更全面地仿真微喷装置工作全过程，直观体现尺寸参数、工作液体性质和驱动参数等输入条件，也能直接反映出单个条件的作用效果。相对于单纯分析流体模型，多场耦合模型为微喷过程的仿真分析研究提供了更好的工具。

(2)本文中所建立的微喷装置数值模型能够较好地仿真微滴喷射过程，与该装置的实际实验结果吻合，说明该模型设计和算法是合理的。

(3)在微喷的数值模型建模中，整个流体域都可认为是始终处于层流状态；与流体表面张力相关的壁面浸润性等属性是不可忽略的，应当根据具体情况作相应设定以保证仿真结果可靠性。

(4)仿真和实验结果都表明，对于压电驱动的膜片式微喷装置的驱动参数，液滴的喷射速度主要由驱动器形变速度决定，而液滴体积主要由驱动器形变距离决定。

(5)数值模型体现出的系统响应特性与真实实验装置一致，可以用来研究微喷装置的振动波形等相关问题。

[1] CHEN Y, HUANG Y, KUO C, et al. Investigation of Design Parameters for Droplet Generators Driven by Piezoelectric Actuators[J]. International Journal of Mechanical Sciences,2007,49(6):733-740.

[2] KIM C S, PARK S, SIM W, et al. Modeling and Characterization of an Industrial Inkjet Head for Micro-patterning on Printed Circuit Boards[J]. Computers & Fluids,2009,38(3):602-612.

[3] SACHS E, VEZZETTI E. Numerical Simulation of Deposition Process for a New 3D Printhead Design[J]. Journal of Materials Processing Technology,2005,161(3):509-515.

[4] 习俊通，周诗贵，王堃. 压电驱动膜片式高温热熔微喷点胶装置,中国：CN201210465518.3[P].2013-3-13. XI Juntong, ZHOU Shigui, WANG Kun. High-temperature-melting Spray Dispensing Equipment of Piezoelectric Actuated Diaphragm-driven, China: CN201210465518.3[P].2013-3-13.

[5] 阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006. YAN Chao. Methods and Applications of Computational Fluid Dynamics[M]. Beijing: Beihang University Press, 2006.

[6] LAUNDER B E, SPALDING D B. Lectures in Mathematical Models of Turbulence[M]. London: Academic Press, 1972.

[7] FINNEMORE J E, FRANZINI J B. Fluid Mechani-cs[M]. Columbus, Ohio: McGraw-Hill,2002.

[8] 李战华，崔海航. 微尺度流动特性[J]. 机械强度,2001,23(4):476-480. LI Zhanhua, CUI Haihang. Characteristics of Micro Scale Flow[J]. Journal of Mechanical Strength,2001,23(4):476-480.

[9] 刘赵淼，逄燕. 不同压力差下微通道尺寸和表面粗糙度对摩擦系数的影响[J]. 工程力学,2012,29(5):200-205. LIU Zhaomiao, PANG Yan. Influences of Size and Roughness of Microchannels on Friction Factors Under Different Pressures[J]. Engineering Mechanics,2012,29(5):200-205.

[10] 李凡，仲伟虹，张佐光，等. 连续纤维复合材料快速原型工艺基础研究[J]. 中国机械工程,2001,12(12):1415-1417. LI Fan, ZHONG Weihong, ZHANG Zuoguang, et al. Preliminary Research on Rpm for the Continuous Fiber Reinforced Composite[J]. China Mechanical Engineering,2001,12(12):1415-1417.

[11] 周诗贵，习俊通. 压电驱动膜片式微滴喷射仿真与尺度一致性试验研究[J]. 机械工程学报,2013,49(8):178-185. ZHOU Shigui, XI Juntong. Simulation and Experiment Study on Piezoelectric Actuated Diaphragm-driven Microdroplet Jetting[J]. Chinese Journal of Mechanical Engineering,2013,49(8):178-185.

[12] KIM B, KIM S, LEE J, et al. Dynamic Characteristics of a Piezoelectric Driven Inkjet Printhead Fabricated Using MEMS Technology[J]. Sensors and Actuators A: Physical,2012,173(1):244-253.

[13] KHALATE A A, BOMBOIS X, BABU KA R, et al. Performance Improvement of a Drop-on-demand Inkjet Printhead Using an Optimization-based Feedforward Control Method[J]. Control Engineering Practice,2011,19(8):771-781.

(编辑 袁兴玲)

Multi-field Coupling Numerical Model and Its Applications of Piezoelectric Actuated Diaphragm-driven Microjet

WANG Kun1XI Juntong1,2

1.School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai, 200240 2.State Key Laboratory of Mechanical System and Vibration, Shanghai,200240

A multi-field coupling numerical model was presented based on an actual structure of a piezoelectric actuated diaphragm-driven microjet printhead that designed and manufactured by the authors. The effects of each parameters were studied in the model. Some important problems of the model such as the judgement of turbulent flow and the effects of the surface force were considered. The relations among the driving wave forms and the droplet properties and the pressure changes in the chamber during a working period were studied with this model.

piezoelectric actuated； diaphragm-driven microjet printhead; numerical simulation; drop-on-demond

2015-11-09

国家自然科学基金资助项目(50975178)

TH16

10.3969/j.issn.1004-132X.2017.02.017

王 堃，男，1983年生。上海交通大学机械与动力工程学院博士研究生。主要研究方向为压电驱动微喷系统的设计、建模与优化、流固耦合数值仿真模型等。E-mail:wang.kun@aliyun.com。习俊通，男，1963年生。上海交通大学机械与动力工程学院教授、博士研究生导师。