变刚度钢板弹簧加速寿命试验程序载荷谱编制

韩为铎 卢剑伟 龙道江

1.合肥工业大学机械与汽车工程学院，合肥，2300092.江淮汽车股份有限公司技术中心，合肥，230601

变刚度钢板弹簧加速寿命试验程序载荷谱编制

韩为铎1卢剑伟1龙道江2

1.合肥工业大学机械与汽车工程学院，合肥，2300092.江淮汽车股份有限公司技术中心，合肥，230601

考虑钢板弹簧总成大变形非线性刚度特性，提出一套适用于钢板弹簧总成的加速寿命试验程序载荷谱编制方法。通过实车试验采集了钢板弹簧总成载荷输入点的加速度载荷谱，结合有限元方法分析了簧片上任意一点的应力载荷谱，发现应力幅值服从Weibull分布，但均值不服从常规的正态分布或Weibull分布，基于获得的分布规律对此类型载荷谱编制方法及台架实现方式进行了探讨。对比发现，编制的加速寿命试验程序载荷谱能够很好地复现路试结果。

非线性的;钢板弹簧;加速寿命;载荷谱;

0 引言

钢板弹簧大量应用于商用车和部分乘用车的非独立悬架中，作为连接车桥与车身的关键总成，在车辆行驶中不断承受着较为复杂的载荷作用，疲劳可靠性面临巨大挑战。

当前，车辆制造企业对钢板弹簧总成的可靠性检验主要采取以下两种方法：一是在专用的强化道路试验场进行整车试验，直至钢板弹簧断裂；二是利用台架试验，采用交变载荷往复循环加载至钢板弹簧断裂。两种方法各有优缺点，前者更接近于实际工况，但为了避免偶然因素干扰，往往需要增加试样数量，成本较高；后者便于实施，但由于采用常幅加载，不能完全反映实际工况特点，导致可信度略逊。因此，如何将道路试验与台架试验的优点相结合成为当前研究的热点之一。

针对钢板弹簧总成的可靠性评价及试验方法，国内外学者进行了大量研究并取得了重要进展[1-2]。随着载荷谱编制方法的快速发展[3-5]，研究人员开始将其应用于汽车零部件的载荷谱处理，并取得了较为理想的效果[6-8]。由于变刚度钢板弹簧总成存在装配预应力、载荷-变形非线性、应变不易测量等因素，因此其载荷谱编制工作具有更大的挑战。

本文以某国产MPV后悬架变刚度钢板弹簧总成为对象，通过载荷谱编制的方法获得了适用于钢板弹簧总成台架加速寿命试验的程序载荷谱，并将所得结果与路试结果进行对比分析。

1 应力谱分析

钢板弹簧总成在役状态下，路面冲击以及车身自重的作用使得各簧片之间相互挤压，导致钢板弹簧的应变信号不易直接采集。本文以某MPV后钢板弹簧为研究对象，选择易于采集的加速度信号作为原始采集信号。信号采集工作于定远试验场强化路段进行。

对采集的加速度信号进行频域积分等处理，可以获得在整个强化路段上弧高相对于初始状态的时间历程信号ΔH。通过有限元分析可以得到钢板弹簧上任意一点应力S与形变ΔH之间的对应关系：

S=g(ΔH)

(1)

由于钢板弹簧装配时受到中心螺栓及板簧座的夹紧作用，因此有限元建模必须考虑簧片所受预应力，满载工况下的应力分布如图1所示。在装配状态的基础上，通过施加不同轴荷作用，即可获得不同轴荷作用下的弧高及应力大小，即获得了某点应力S与形变ΔH之间的对应关系。

图1 满载工况下应力结果Fig.1 Stress result under full load condition

综合形变信号及应力-形变响应关系，可得到路面随机激励下钢板弹簧任意一点的应力谱。满载时最大应力点的应力谱如图2所示。

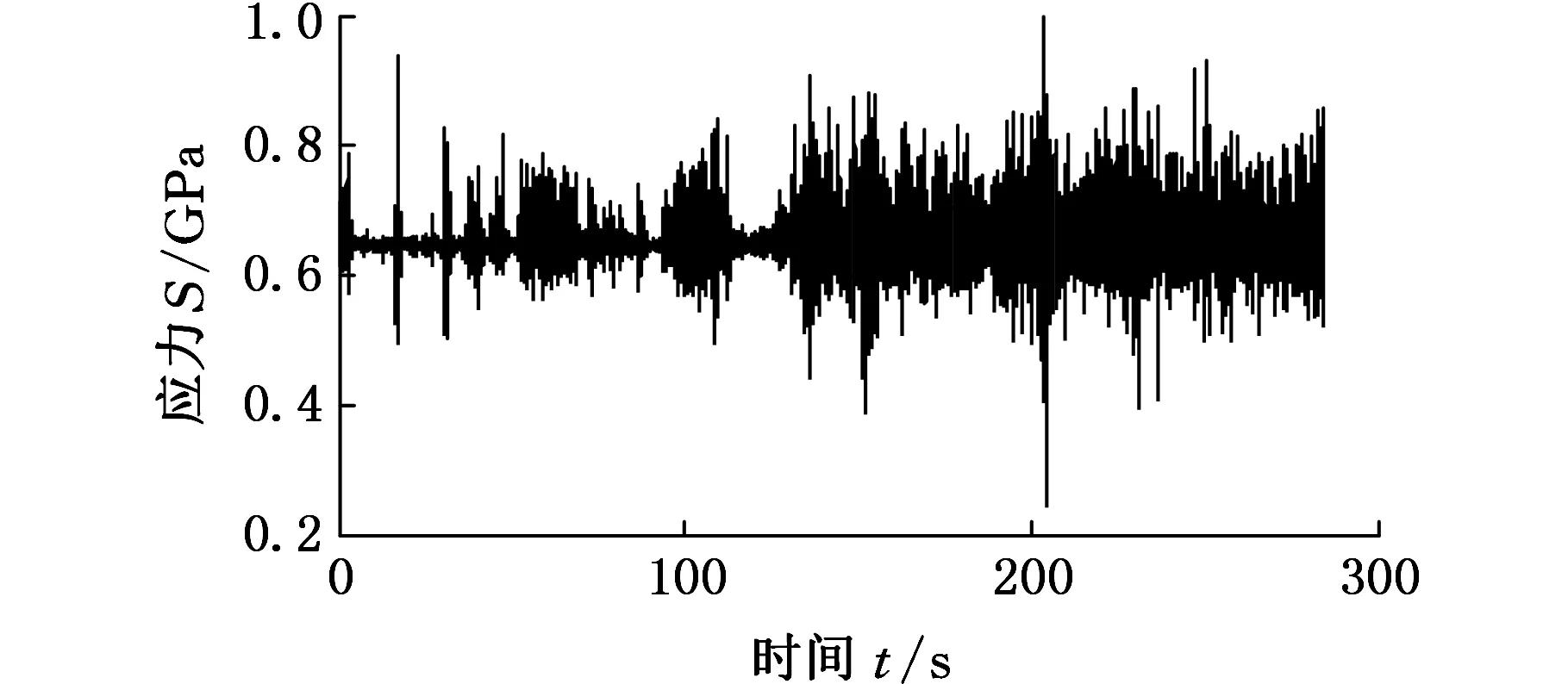
图2 随机路面下某点的应力载荷谱Fig.2 Stress load spectrum of a point under random road

下文将对此应力载荷谱进行编制处理，探讨台架加速寿命试验程序载荷谱的编制过程。

2 载荷谱统计特性

为获得上述应力谱的统计特性，需对其进行循环计数，即将载荷谱精简成若干个全循环或者半循环。本文采用三参数雨流计数法[9]对上述应力谱进行统计处理，得到图3所示的均值-幅值三维柱状图。

图3 均幅值三维柱状图Fig.3 Histogram of mean and amplitude

应用统计学方法对雨流计数结果进行分析是获得载荷谱分布特征的主要途径[10]。图4、图5分别为应力谱幅值和均值的直方图，发现幅值总体分布特征与Weibull分布相吻合，均值总体分布特征与正态分布或三参数Weibull分布相吻合，即与前人研究结果[11-12]相符合。因此初步假设幅值服从Weibull分布，均值服从正态分布或Weibull分布。

图4 幅值直方图Fig.4 Histogram of amplitude

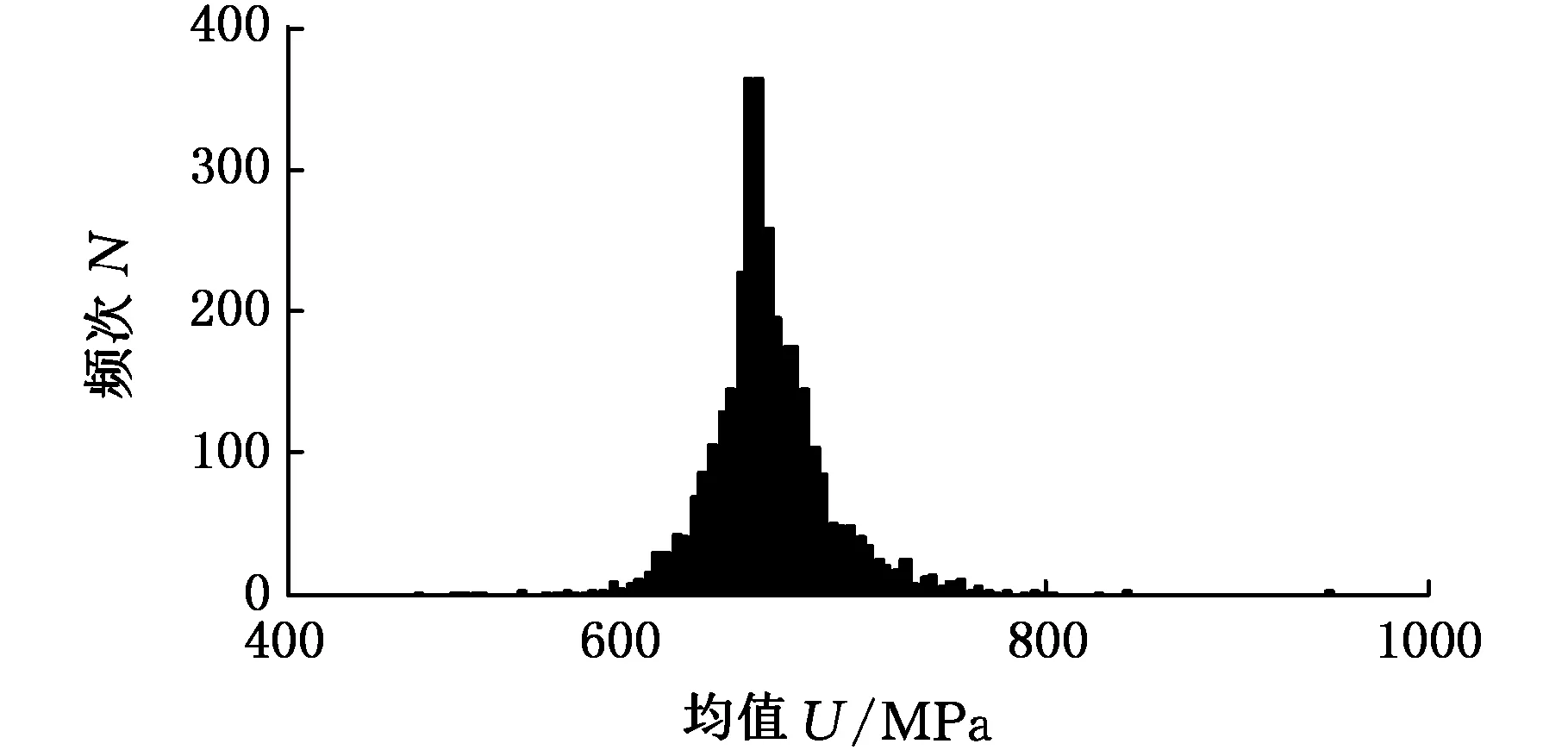
图5 均值直方图Fig.5 Histogram of Mean

为进一步验证该假设，分别在Weibull分布坐标纸和正态分布坐标纸中绘制其幅值、均值数据，结果如图6～图8所示。

图6 幅值Weibull分布概率图Fig.6 Amplitude probability map under Weibull distribution

图7 均值正态分布概率图Fig.7 Mean probability map under normal distribution

图8 均值Weibull分布概率图Fig.8 Mean probability map under Weibull distribution

从图6中可以看出，应力幅值分布与Weibull分布标准线重合度较高，可以认为前述幅值Weibull分布的假设成立。均值的实际数据分布与正态分布标准线或Weibull分布标准线有较大偏离，尤其在小概率均值段(图7、图8)。因此，利用正态分布或Weibull分布对钢板弹簧在随机路面激励下的应力均值进行拟合并不能达到理想的效果。

由于幅值服从Weibull分布，因此使用Weibull分布进行拟合，其概率密度函数的表达式为

(2)

式中，a为形状参数;b为尺度参数;c为位置参数。

幅值的Weibull分布拟合结果为a=0.6408，b=9.1275，c=0。

应力均值并不满足常规的正态分布或Weibull分布，无法使用参数估计方法拟合其分布特征。非参数估计方法中，核密度估计可以充分考虑变量的统计特性并使概率密度曲线趋于光滑，在估计随机变量概率密度函数方面较之其他非参数估计方法具有一定优势[13]。基于此，本文采用非参数核密度估计方法求应力均值的概率密度函数。设来自一维随机变量Y的样本为Y1，Y2，…，Yn，则Y的核密度估计函数为

(3)

式中，n为样本容量；h为带宽系数；K(·)为核函数。

对于本文的应力均值分布特征，采用非参数核密度估计后的概率密度函数如图9所示。

图9 应力均值核密度估计结果Fig.9 Kernel density estimation result of stress mean

为求得幅值与均值的联合概率密度函数，有必要对均值与幅值的独立性进行验证。

假设H0应力幅值与均值相互独立。

根据Fisher定理，样本的检验统计量是近似服从自由度为(r-1)(s-1)的χ2分布：

(4)

式中，r、s分别为应力幅值及均值的分级数，此处皆取100；ni为幅值落在i级的频次；nj为均值落在j级的频次；nij为幅值落在i级、均值落在j级的频次。

当检验统计量的自由度较大时，χ2分布近似服从正态分布N(m，2m)。因此可由

(5)

式中，Uα为标准正态分布的上α分位数;m为χ2分布的均值，m=(r-1)(s-1)=9801。

近似求出χ2分布上的α分位点。

3 程序载荷谱编制

3.1 二维载荷谱编制

根据前文得到的载荷谱结果及其统计特性，在简化载荷谱的同时保留其疲劳特性，是疲劳载荷谱编制的核心环节。由于试验场采集数据有限，不能完全反映载荷谱的统计特性。所以在载荷谱编制之前，有必要将载荷谱外推以求得具有统计意义的载荷谱极值。本文采用目前应用最广泛的参数外推法对载荷谱予以外推[14]。参数法根据样本估计总体的分布规律，再根据总体的分布规律对有限的样本进行外推，大量工程实践验证了该方法的有效性。本文将采集到的载荷谱长度外推100倍，即外推载荷谱的强化路面当量行驶里程为650 km。车辆在强化路面行驶100个循环工况可能出现的载荷极值可由其统计特性估计。由雨流计数结果，一个循环工况下的载荷循环次数为3217，故外推之后载荷极值的出现概率P=1/(3217×100)= 3.11×10-6。由于幅值与均值相互独立，故幅值的最大值为

(6)

由于应力均值的概率密度函数已由非参数核估计方法获得，故极值可由其分布函数反求得出：

(7)

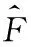
根据式(6)、式(7)计算的幅值最大值Amax=480.7 MPa，均值最大值Umax=875.9 MPa。幅值与均值的最小值Amin、Umin的求解方法与最大值求解方法相同，同样利用极值出现概率 P获得，在此不再赘述。

Conover研究发现，将载荷谱分成8级可以充分反映其疲劳特性，这八级载荷的幅值比例分别是1.000、0.950、0.850、0.725、0.575、0.425、0.275、0.125。将幅值按以上比例划分成不等间隔的8级，将均值划分成等间隔的8级，便将整个载荷谱编制成一个8×8的载荷矩阵，即二维载荷谱。

由于幅值与均值相互独立，故其联合概率密度函数为

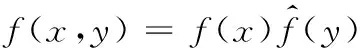
(8)

在联合概率密度函数已知的基础上，各等级循环次数为

(9)

式中，N为外推之后的循环次数；i为均值级数；j为幅值级数；mi、mi+1分别为第i组均值的上下限；rj、rj+1分别为第j组幅值的上下限。

二维载荷谱计算结果如表1所示。

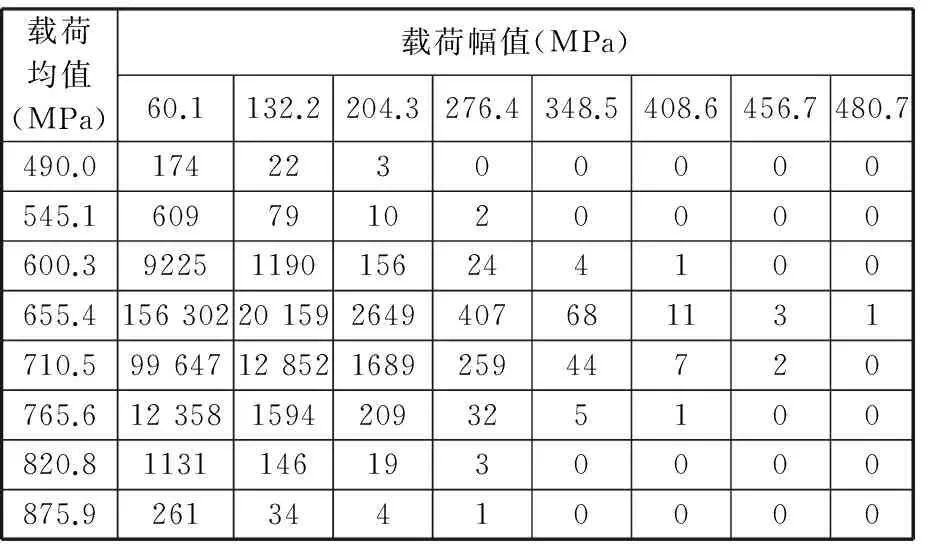
表1 二维程序载荷谱Tab.1 Two dimensional program load spectrum

3.2 一维载荷谱编制

在上述二维程序载荷谱基础上，采用变均值法编制易于实现的一维程序载荷谱。根据文献[11]，给定幅值情况下，一维载荷谱的均值：

(10)

式中，mj为二维载荷谱中第i组均值。

计算结果如表2所示。

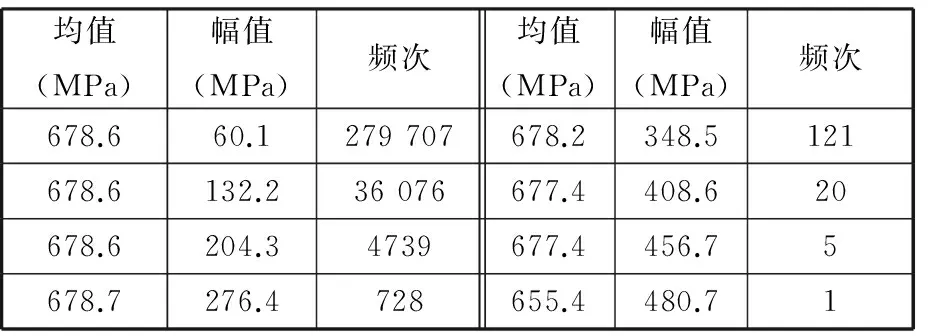
表2 一维程序载荷谱Tab.2 One dimensional program load spectrum

由损伤累积理论可知，疲劳极限60%以下的应力对疲劳结果几乎不造成影响[15]。因此，为了进一步精简载荷谱，在计入平均应力对疲劳影响的前提下，剔除疲劳极限60%以下的载荷。剔除小载荷之后的载荷谱长度缩减为原载荷谱的1/190，加速效果明显。最终得到采用低-高-低加载顺序的载荷谱，如图10所示。

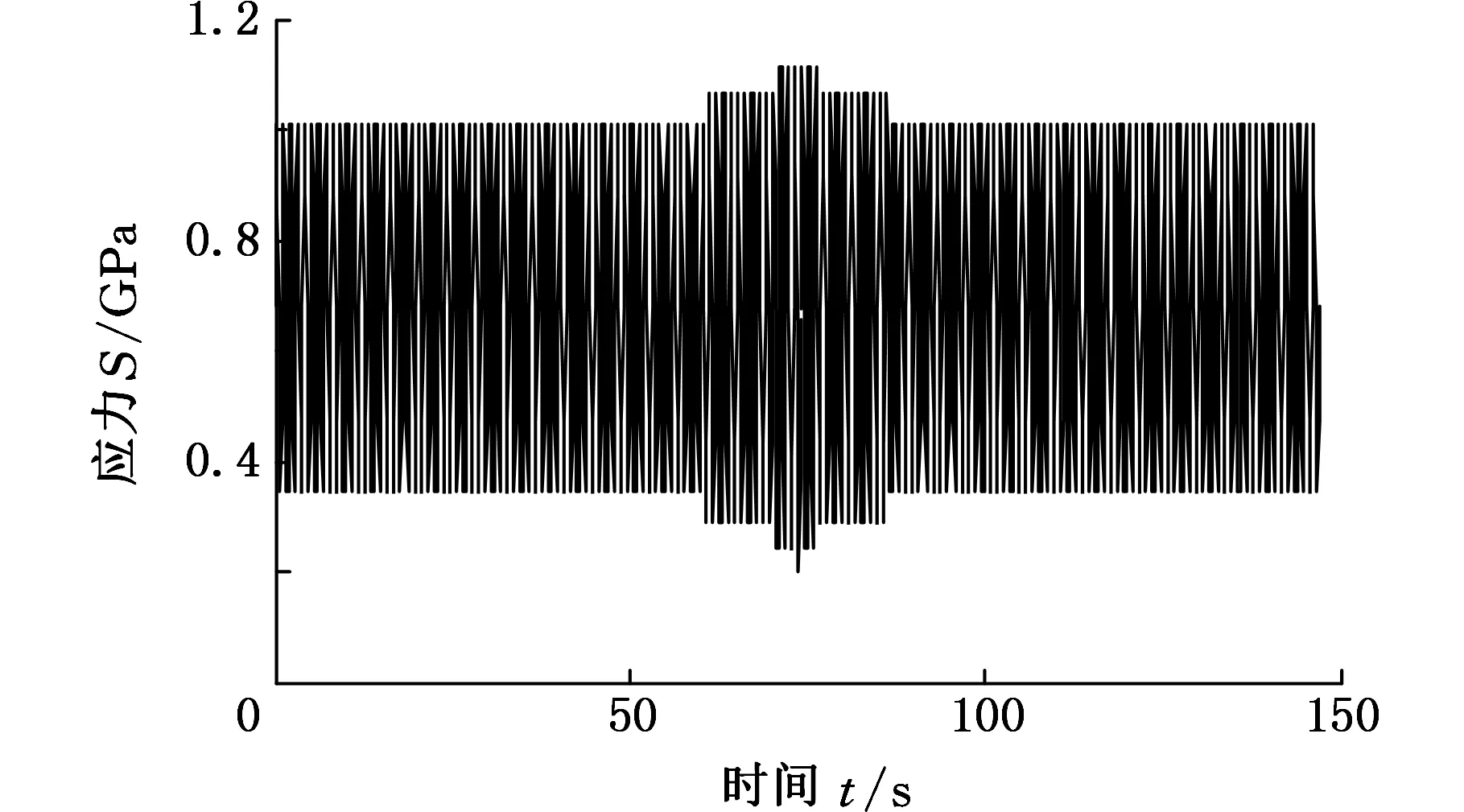
图10 一维程序载荷谱Fig.10 One dimensional program load spectrum

应力程序载荷谱还不能直接用于台架试验的加载，为此，应用前述的应力-形变响应函数，对应力载荷谱进行转换。在已知应力水平S时，板簧总成相对于满载状态的形变ΔH可由式(1)求出，结果如图11所示。基于此函数，便可将表2中的一维应力程序谱变换为台架试验需要的一维位移程序载荷谱。

图11 形变-应力关系Fig.11 Relation between deformation and stress

进行加速寿命试验时，首先依据后桥轴荷，在台架上将钢板弹簧总成加载至满载状态并以当前状态进行位移归零标定，然后以上述一维位移载荷谱作为试验台驱动程序载荷谱，进行加载测试。

上述程序载荷谱仅对采集加速度谱所用的钢板弹簧总成有效。钢板弹簧的设计参数发生改变，整车的振动响应特性也将发生变化，从而导致之前得到的载荷谱失真。为此，需要结合设计参数对钢板弹簧形变的影响规律，进行必要的修正，具体流程在此不再赘述。

4 程序载荷谱疲劳结果与路试结果对比分析

强化道路进行整车可靠性测试时，钢板弹簧的失效模式主要表现为第2片前段以及第3片前段断裂失效(第3片寿命往往低于第2片寿命)，部分失效部位如图12所示。

(a)第3片簧片断裂图

(b)第2片簧片断裂图图12 簧片道路试验断裂图Fig.12 Road test result of leaf springs

下面分别以采集的载荷谱和编制的一维程序载荷谱对钢板弹簧簧片进行疲劳分析。板簧材料为60Si2Mn，采用Goodman平均应力修正以及线性累积损伤准则，将采集谱和编制的一维程序载荷谱分别代入50%存活率下的S-N曲线进行损伤计算。计算以6.5 km强化道路为一个工况循环，将完成的工况循环次数作为疲劳寿命指标，结果如表3所示。

表3 载荷谱编制前后簧片可循环次数Tab.3 Cycles before and after load spectrum compiling

上述结果说明，相对于采集谱的作用结果，编制谱寿命结果偏于保守，但与道路试验吻合较好，且不同簧片的相对寿命保持一致。由此可以得出结论：依据本文给出的程序载荷谱能够有效反映板簧总成的失效形式。

5 结论

(1)强化随机路面激励下，变刚度钢板弹簧的应力幅值服从二参数Weibull分布，均值并不与其他汽车零部件一样服从正态分布或三参数Weibull分布。

(2)采用非参数核密度方法估算钢板弹簧应力均值的概率密度函数能够有效体现其分布特性，便于进行载荷谱外推等工作。

(3)提出了完整的钢板弹簧总成台架加速寿命试验程序载荷谱编制方法。采用编制的载荷谱对钢板弹簧进行寿命核算，经与某车型钢板弹簧道路试验结果对比，发现其能够很好地复现钢板弹簧失效部位和失效里程，并能大幅降低可靠性试验成本。

[1] KONG Y S, OMAR M Z, CHUA L B, et al. Fatigue Life Prediction of Parabolic Leaf Spring under Various Road Conditions[J]. Engineering Failure Analysis, 2014, 46: 92-103.

[2] 朱茂桃, 熊梦锦, 何志刚, 等. 钢板弹簧疲劳分析[J]. 农业机械学报, 2006, 37(3): 149-152. ZHU Maotao, XIONG Mengjin, HE Zhigang, et al. Fatigue Analysis for Leaf Spring[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(3): 149-152.

[3] HEULER P, KLATSCHKE H. Generation and Use of Standardised Load Spectra and Load-time Histories[J]. International Journal of Fatigue, 2005, 27(8): 974-990.

[4] JOHANNESSON P, SVENSSON T, De MARE J. Fatigue Life Prediction Based on Variable Amplitude Tests—Methodology[J]. International Journal of Fatigue, 2005, 27(8): 954-965.

[5] 卢曦, 郑松林. 考虑小载荷强化的汽车构件疲劳累积损伤试验研究[J]. 中国机械工程, 2007, 18(8): 994-997. LU Xi, ZHENG Songlin. Experimental Investigation on Cumulative Fatigue Damage of Strengthening under Low Amplitude Loading for Automobile Structures[J]. China Mechanical Engineering, 2007, 18(8): 994-997.

[6] 于佳伟, 郑松林, 赵礼辉, 等. 整车室内道路模拟试验用载荷谱的编制方法研究[J]. 机械工程学报, 2015, 51(14): 93-99. YU Jiawei, ZHENG Songlin, ZHAO Lihui, et al. Research on Spectrum Development Methodology for Vehicle Indoor Road Simulation Test[J]. Journal of Mechanical Engineering, 2015, 51(14): 93-99.

[7] 沈永峰, 郑松林, 王治瑞, 等. 某型轿车摆臂程序载荷谱编制研究[J]. 中国机械工程, 2013, 24(14): 1974-1978. SHEN Yongfen, ZHENG Songlin, WANG Zhirui, et al. Research on Compilation of Automotive Swing Arm Program Spectrum[J]. China Mechanical Engineering, 2013, 24(14): 1974-1978.

[8] 赵晓鹏, 张强, 姜丁, 等. 某型越野车试验场载荷谱的压缩与外推[J]. 汽车工程, 2009 (9): 871-875. ZHAO Xiaopeng, ZHANG Qiang, JIANG Ding, et al. The Compression and Extrapolation of Load Spectrum for a Heavy Off-road Vehicle Obtained from Proving Ground Testing[J]. Automotive Engineering, 2009 (9): 871-875.

[9] POWER E. Cycle Counting Methods and the Development of Block Load Fatigue Programmes[J]. SAE Technical Paper, 1978:780102.

[10] 高镇同. 疲劳应用统计学[M]. 北京：国防工业出版社, 1986. GAO Zhentong. Statistics of Fatigue Application[M]. Beijing: National Defence Industry Press, 1986.

[11] 高云凯, 徐成民, 方剑光. 车身台架疲劳试验程序载荷谱研究[J]. 机械工程学报, 2014, 50(4): 92-98. GAO Yunkai, XU Chengmin, FANG Jianguang. Study on the Programed Load Spectrum of the Body Fatigue Bench Test[J]. Journal of Mechanical Engineering, 2014, 50(4): 92-98.

[12] 熊峻江, 高镇同. 实测载荷谱数据处理系统[J]. 北京航空航天大学学报, 1996, 22(4): 438-441. XIONG Junjiang, GAO Zhentong. Actual Load Spectrum Data Treatment System[J]. Journal of Beijing University of Aeronautics and Astronautics, 1996, 22(4): 438-441.

[13] 汤阿妮. 基于核密度估计算法的飞机载荷谱统计技术[J]. 北京航空航天大学学报, 2011, 37(6): 654-657. TANG Ani. Technique of Aircraft Loads Spectrum Statistics Based on Kernel Density Estimation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(6): 654-657.

[14] JOHANNESSON P. Extrapolation of Load Histories and Spectra[J]. Fatigue & Fracture of Engineering Materials & Structures, 2006, 29(3): 209-217.

[15] HEULER P, SEEGER T. A Criterion for Omission of Variable Amplitude Loading Histories[J]. International Journal of Fatigue, 1986, 8(4): 225-230.

(编辑 张 洋)

Test Program Load Spectrum Compilation for Accelerated Life Test of Leaf Springs with Variable Stiffness

HAN Weiduo1LU Jianwei1LONG Daojiang2

1.School of Mechanical and Automotive Engineering,Hefei University of Technology,Hefei，230009 2.Passenger Car of Research Center，Auhui Jianghuai Automobile Co.,Ltd.，Hefei，230601

Considering characteristics of large deformation and nonlinear stiffness, a method of test program load spectrum compilation suitable for accelerated life test(ALT) of nonlinear leaf springs was presented. Based on the acceleration spectrum exposed to the leaf spring by road test, FEA method was used to obtain stress spectrum at any point. It is found that the amplitudes of stresses obey Weibull distribution，but the mean is not distributed as normal distribution or Weibull distribution. Based on the extrapolated spectrum, method of compilation and realization for bench test was studied. Compared to the results of road test, the compiled ALT program load spectrum is in accordance with the road tests.

nonlinear; leaf spring; accelerated life; loading spectrum

2016-03-02

教育部新世纪优秀人才支持计划资助项目(NCET-10-0358)；安徽省高校自然科学研究重大项目(KJ2014ZD06)

TH135;U463.334

10.3969/j.issn.1004-132X.2017.02.004

韩为铎，男，1991年生。合肥工业大学机械与汽车工程学院硕士研究生。主要研究方向为汽车耐久性设计。卢剑伟(通信作者)，男，1975年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。E-mail: jwlu75@163.cm。龙道江，男，1986年生。江淮汽车股份有限公司技术中心工程师。