宽频压电振动能量采集器的分布参数模型与实验

杨斌强 徐文潭 陆国丽 王光庆

浙江工商大学信息与电子工程学院，杭州，310018

宽频压电振动能量采集器的分布参数模型与实验

杨斌强 徐文潭 陆国丽 王光庆

浙江工商大学信息与电子工程学院，杭州，310018

为解决无线传感网络节点自供电问题，提出了一种带有弹性支撑与放大的宽频压电振动能量采集器。利用Hamilton原理和Raleigh-Ritz方法，并考虑悬臂梁末端质量块的影响，建立了压电能量采集器的分布参数机电耦合模型；数值分析了能量采集器质量比、刚度比和阻尼比等参数对系统振动特性、输出特性的影响；研制了实验原理样机，搭建了实验测试平台，验证了数学模型的正确性。研究结果表明，分布参数模型比集总参数模型具有更高的预测精度。

压电能量采集；两自由度；分布参数模型；弹性放大器；宽频带

0 引言

振动能量采集技术在无线传感网络及MEMS器件中具有广阔的应用前景，它可以解决上述器件使用电池供电带来的电池寿命短、更换不方便、污染环境等诸多弊端。振动能量采集器根据转换机理不同分为静电式、电磁式和压电式三种，相比而言，压电式结构更简单、能量转换密度更高[1]。

压电振动能量采集器(piezoelectric vibration energy harvester, PVEH) 一般由压电双晶片或压电单晶片悬臂梁构成，是单自由度 (single degree of freedom，SDOF) 系统。ERTURK等[2-3]考虑末端质量块的影响，建立了SDOF能量采集器机电耦合分布参数模型，分析了负载电阻和机电耦合系数对采集器输出性能的影响，并指出利用集总参数模型预测采集器末端振动位移将产生较大误差(主要源于分布参数对激励信号幅值的影响)的问题。由于环境振动频率是随机的，而线性谐振的SDOF压电能量采集器工作频带窄，谐振频率难以和环境振动频率完全匹配，导致机电能量转换效率较低。为此，TANG等[4]提出了一种两自由度(two degrees of freedom，TDOF)的宽频压电振动能量采集器，优化了输出功率，但忽略了悬臂梁轴向应变分布和振型对输出性能的影响。ALDRAIHEM等[5]利用Lagrangian 动力学方法建立了一种带有弹性放大器的压电振动能量采集器模型，分析了系统参数对采集器输出性能的影响，此模型忽略了系统阻尼的影响。MA等[6]设计出一种带质量-弹簧系统的压电振动能量采集器，并建立集总参数模型，但模型忽略了压电元件机电耦合效应。WANG等[7]提出了一种带单自由度线性放大器的压电能量采集器，利用能量方法建立了采集器机电耦合模型，并用有限元建模进行了验证，此模型未考虑悬臂梁末端质量块的影响。喻其炳等[8]设计了一种多频响应的压电振动能量采集器，制作了样机，通过实验证明了其可以在更宽的频带范围内采集更多的振动能量。王光庆等[9]提出了一种宽频压电能量采集器改进的集总参数解析模型，并进行了验证。

虽然改进的模型考虑到了能量采集器的机电耦合输出效应，但模型忽略了压电悬臂梁的分布参数和动态振型对输出性能的影响，因此，该模型的预测精度不是很高。另外，集总参数模型主要考虑压电采集器的一阶谐振特性，认为一阶谐振状态下，压电采集器可等效成一个由质量-弹簧-阻尼构成的集总参数模型。但是对于宽频压电系统而言，集总参数模型无法准确反映出高阶谐振特性对采集器输出性能的影响，也无法反映出采集器高阶谐振状态与一阶谐振状态之间的耦合关系。为此，针对带有弹性支撑与放大的两自由度宽频压电振动能量采集器，笔者利用Hamilton原理和Raleigh-Ritz方法，考虑悬臂梁末端质量块、悬臂梁分布参数和动态振型的影响，建立了宽频压电振动能量采集器的分布参数机电耦合模型，数值分析了压电能量采集器分布参数(质量比、刚度比和阻尼比等)对系统振动特性和能量采集输出特性的影响。最后，研制了原理样机，搭建了实验测试平台，并对模型进行了验证。

1 理论模型

1.1 结构设计

TDOF压电能量采集器的结构模型如图1所示，它由双压电晶片悬臂梁振动能量采集器和一个弹性放大器组成。两压电晶片(PZT1和PZT2)分别黏结在金属基板的上下表面，它们的电极化方向相反且与z轴平行。压电悬臂梁的一端连在基座上的弹性放大器，另一端连着质量为mt的末端质量块，RL为输出负载电阻。mb、Kb、Cb分别为弹性放大器的质量、弹簧刚度和阻尼系数。L为悬臂梁的长度，b为悬臂梁宽度。hp、hs分别为PZT厚度和基板厚度。

图1 TDOF压电能量采集器结构模型Fig.1 Schematic of TDOF PVEH

假定压电晶片与金属基板是完好黏结的，且压电悬臂梁是Euler Bernoulli梁，做横向弯曲振动(沿z轴方向)，则TDOF压电能量采集器中金属基板满足本构关系：

σs=csεs

(1)

压电片PZT满足本构关系：

(2)

1.2 运动控制方程

根据Hamilton原理，该模型的运动方程为

(3)

式中，t为时间；ΔT为系统动能变化量；ΔU为系统内势能变化量；ΔWe为电势能变化量；ΔW为外力做功。

系统动能为

(4)

式中，meq为压电梁(含末端质量块)的静态质量；yb为集中质量mb相对于基座的运动位移；w为压电梁上各点相对于mb的运动位移。

系统内势能为

(5)

Vp=2ρpLb Vs=ρsLb

式中，Vp为PZT体积；Vs为金属基板体积。

系统电势能为

(6)

外力做功为

(7)

根据Raleigh-Ritz方法，压电梁的横向弯曲位移可以写成[10]：

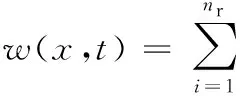
(8)

式中，φri(x)为悬臂梁弯曲振型函数；ri(t)为与时间相关的i阶坐标；nr为振型个数。

φr(x)=C[cosγx-coshγx+ζ(sinγx-sinhγx)]

(9)

γ=λ/L

式中，ρ为压电悬臂梁的平均密度；A为压电悬臂梁的截面面积；λ为悬臂梁一阶弯曲振动的特征值；C为是振型常数。

振型常数C可由下式得到：

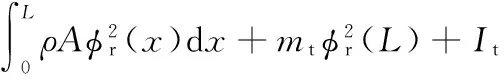
(10)

式中，It为悬臂梁末端集总质量mt绕其质心的转动惯量。

根据Raleigh-Ritz方法，压电悬臂梁的电势为

(11)

(12)

式中，ψVj(x)为第j对电极沿z向的电势分布函数，并假设z=0处的ψVj(x)为0；uj(t)为与时间相关的第j对电极电压；z为沿压电梁厚度方向的坐标。

两个压电单晶片的两端电势差分别为

(13)

式中，U1、U2分别为PZT1和PZT2输出电压，且U1=U2。

将式(4)～式(7)代入式(3)，可得两自由度宽频压电能量采集器的分布参数机电耦合模型方程：

(14)

Bf=∫VsρsφrdVs+∫VpρpφrdVp+mtφr(L)

meq=∫VsρsdVs+∫VpρpdVp+mt

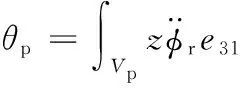
Cb=2mbωbξbCeq=2mωeqξeq

式中，m为压电梁的等效质量；Bf为压电梁的质量函数；Kep为压电梁的等效刚度；θp为压电梁的等效机电耦合系数；Cp为压电梁的静态电容；Cb为弹性放大器阻尼；Ceq为压电梁阻尼。

对式(14)进行Laplace变换，得

(15)

式中，R(S)、Yb(S)、URL(S)和Ub(S)分别为r(t)、yb(t)、URL(t)和ub(t)的Laplace变换函数。

对式(15)求解可以得到如下传递函数：

(16)

(17)

(18)

(19)

(20)

S=jω B1=mb+meq

式中，ω为振动角频率。

2 数值分析

由于宽频压电振动能量采集器是由悬臂梁压电系统和弹性放大器耦合而成的，因此，系统结构参数(质量比、刚度比、阻尼比等)对宽频压电振动能量采集器的输出特性具有重要的影响，所以本文着重讨论了系统中压电能量采集器和弹性放大器的质量比、刚度比和阻尼比对系统输出特性的影响。

(21)

利用MATLAB仿真软件数值分析分布参数机电耦合模型在单位加速度下的振动特性、能量采集输出特性和负载特性。表1所示为用于仿真的压电悬臂梁材料的几何参数。

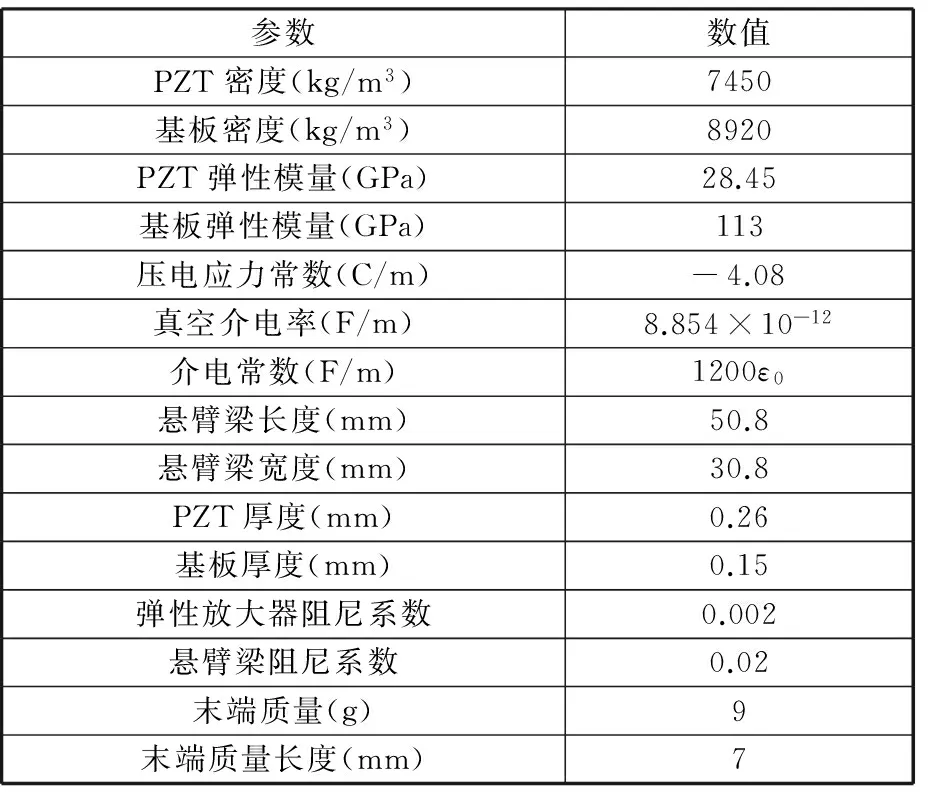
表1 压电梁的材料参数和几何参数Tab.1 Material and geometric properties of piezoelectric beam

2.1 刚度比k对输出特性的影响

图2所示分别为质量比a=10，RL=1 kΩ时，不同刚度比k下悬臂梁末端速度、输出电压和输出功率随频率的变化曲线，为了便于比较，本文末端速度、输出电压和输出功率均表示基础激励加速度为g条件下的输出结果。从图2中可以看出，末端速度、输出电压和输出功率有相同的变化趋势，刚度比k变化时，每条曲线的两峰的横轴位置、峰值、横轴间距也在变化，且左右峰点的幅值随刚度比的增加，呈现先增大、后减小的趋势。对左峰点而言，随着刚度比k增大，弹性放大器刚度增大，对基础振动位移的放大能力增强，悬臂梁末端速度增大，输出电压和输出功率也增大，这表明弹性放大器的部分振动能转换成了压电悬臂梁的机械能。随着k继续增大，输出电压和输出功率反而减小，表明压电悬臂梁的部分机械能转换成了弹性放大器的振动能。k≫a时，由于弹性放大器变成了刚性，放大能力消失，因此，压电悬臂梁的输出电压和输出功率减到最小。

k=a=10时，曲线左右两峰点的横轴间距变得最小，左右两峰形成了一个宽频带窗口。此时，左峰点的幅值却最大，这是因为此时的基础振动频率与弹性放大器的固有频率ωb、悬臂梁固有频率ωeq一致，整个系统处于谐振状态。说明这种情况下，宽频能量采集器具有更宽的有效工作频带和更佳的输出性能。

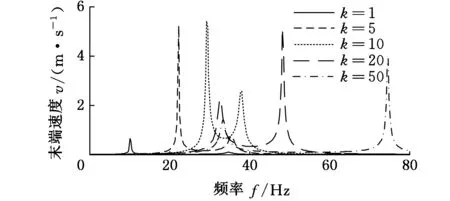
(a)末端速度v随频率f的变化

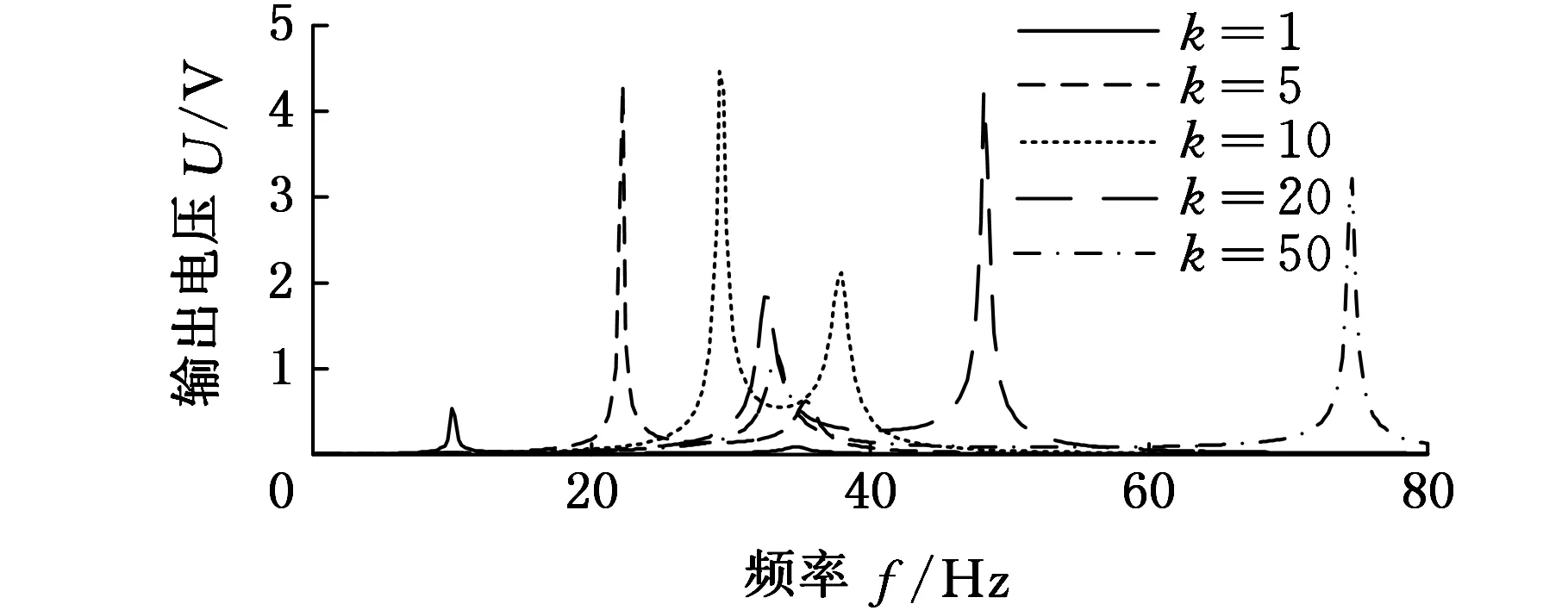
(b)输出电压U随频率f的变化

(c)输出功率P随频率f的变化图2 不同刚度比k下的悬臂梁运动特性和 输出特性的变化(a=10，RL=1 kΩ)Fig.2 Motion and output performance of cantilever beam with different stiffness ratios k when ratios (a=10，RL=1 kΩ)

2.2 质量比a对输出特性的影响

图3所示分别为刚度比k=10，RL=1 kΩ时，不同质量比a下悬臂梁末端速度、输出电压和输出功率随频率的变化曲线。可以看出，末端速度、输出电压和输出功率随质量比a增大的变化趋势，与图2中它们随刚度比k减小的变化趋势相似。主要是因为当a很小时，k≫a，弹性放大器的刚性起主导作用，系统弹性支撑转变为刚性支撑，此时放大器对基础振动位移的放大能力最小。随着a的增大，放大器对基础振动位移的放大能力增强，使得悬臂梁末端速度逐渐增大。当k≪a时，弹性放大器刚度相对很小，对基础振动位移的放大能力不足，导致悬臂梁末端振动速度减小。同样，在a=k=10时，两峰间的横轴间距最小，形成一个宽频窗口。

图4所示为a=k，RL=1 kΩ时，悬臂梁末端速度、输出电压和输出功率随频率的变化曲线。由图4可知，随着a(或k)的增大，曲线左右峰点幅值逐渐增大，左右两峰点之间的横轴间距逐渐减小。可见，在a=k的情况下，大的质量比或刚度比有利于形成具有有效工作频带的宽频窗口，有利于提高系统性能。

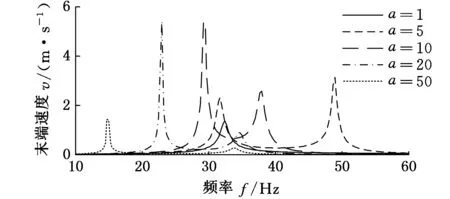
(a)末端速度v随频率f的变化

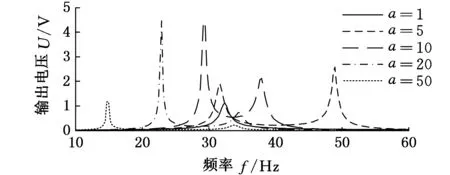
(b)输出电压U随频率f的变化

(c)输出功率P随频率f的变化图3 不同质量比a下的悬臂梁运动特性和 输出特性的变化(k=10，RL =1 kΩ)Fig.3 Motion and output performance of cantilever beam with different mass ratios a when ratios (k=10，RL =1 kΩ)

2.3 阻尼比c对输出特性的影响

图5所示为阻尼比-系统输出功率曲线，可以看出，阻尼比c增大(弹性放大器的阻尼系数增大)，使得系统的输出功率降低，功率输出曲线峰点的幅值对阻尼比的影响非常敏感，阻尼比c增大，峰点幅值急剧减小。当弹性放大器的阻尼系数远大于悬臂梁的阻尼系数时，弹性放大器对基础振动位移的放大功能将消失，此时，曲线两峰点合并成形成一个峰点，这说明小的弹性放大器阻尼系数有利于提高TDOF能量采集器的输出功率。

图6所示为图4 中a=k=10曲线左峰点的时域响应。左峰点频率为29.25 Hz，此时最大输出电压、输出功率(单位加速度为g的激励条件下)分别为4.7 V和20 mW。

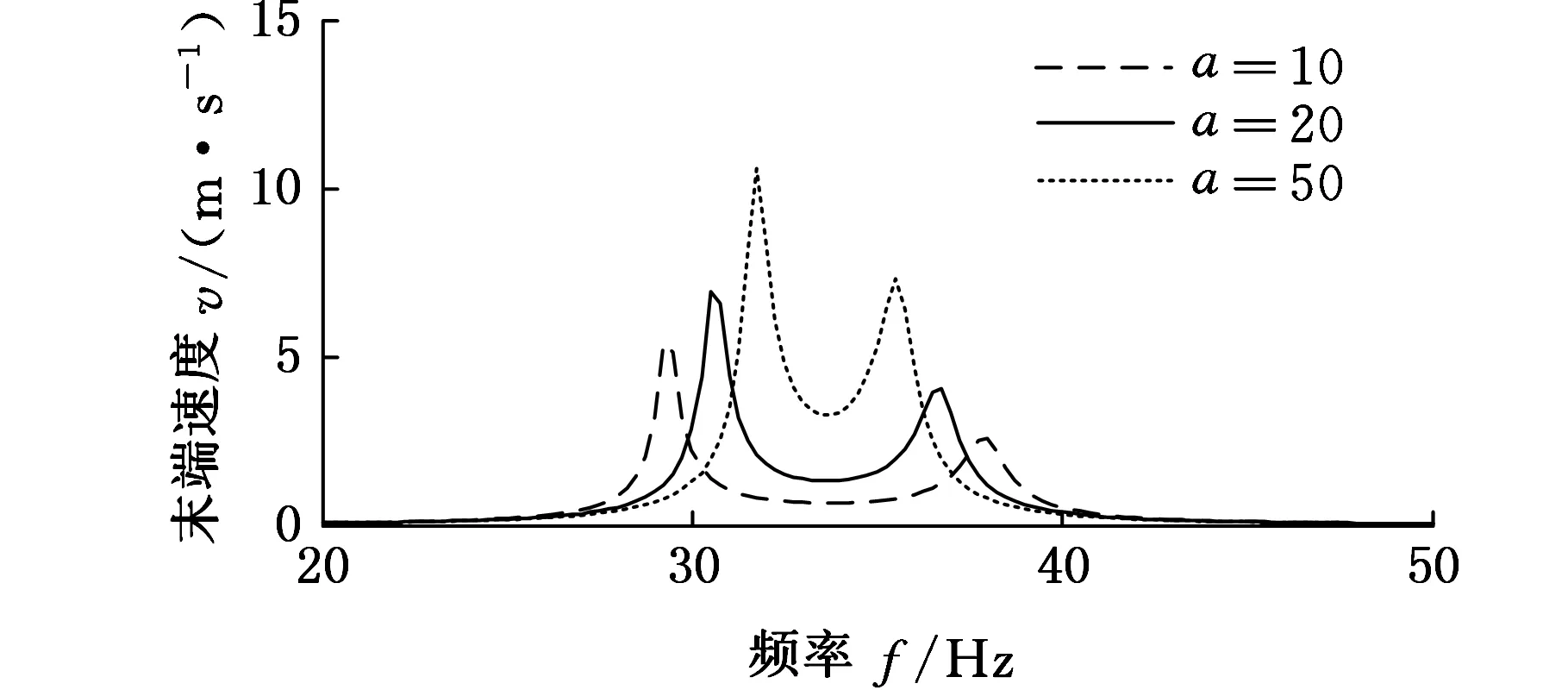
(a)末端速度v随频率f的变化

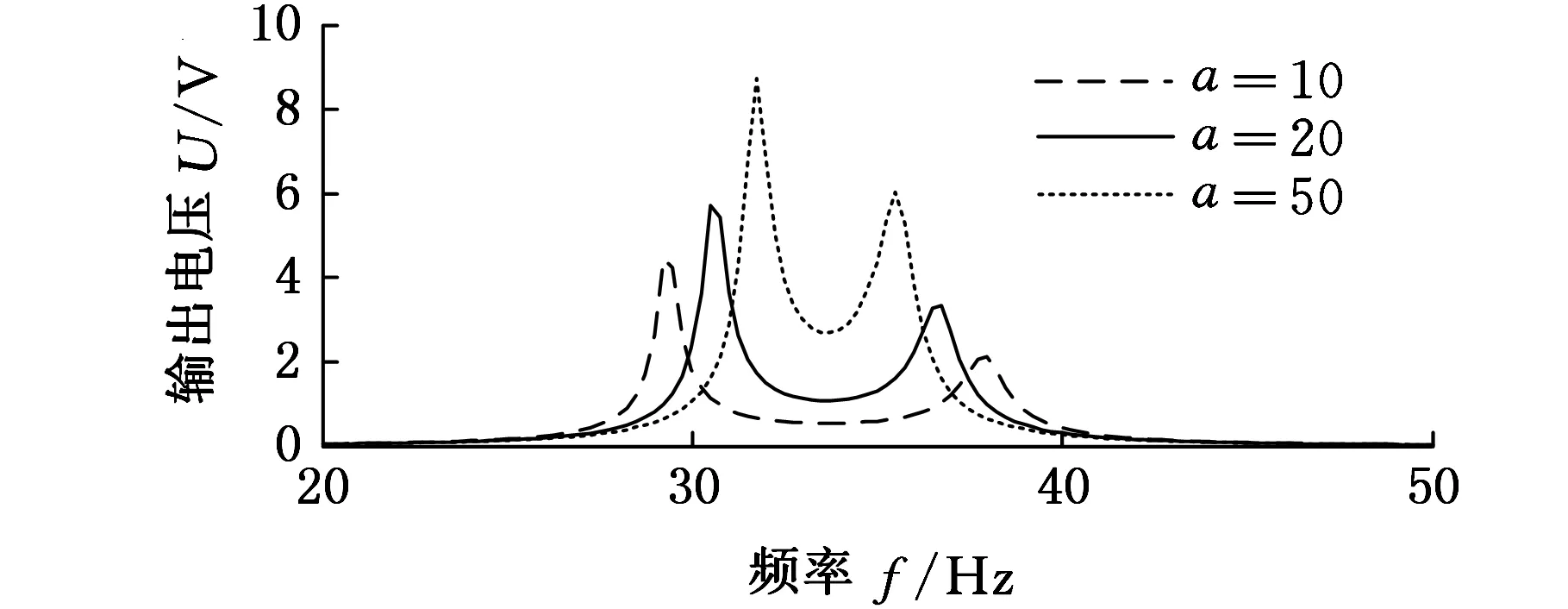
(b)输出电压U随频率f的变化

(c)输出功率P随频率f的变化图4 不同质量比a下的悬臂梁运动特性和 输出特性的变化(a=k，RL =1 kΩ)Fig.4 Motion and output performance of cantilever beam with different mass ratios a when ratios (a=k，RL =1 kΩ)

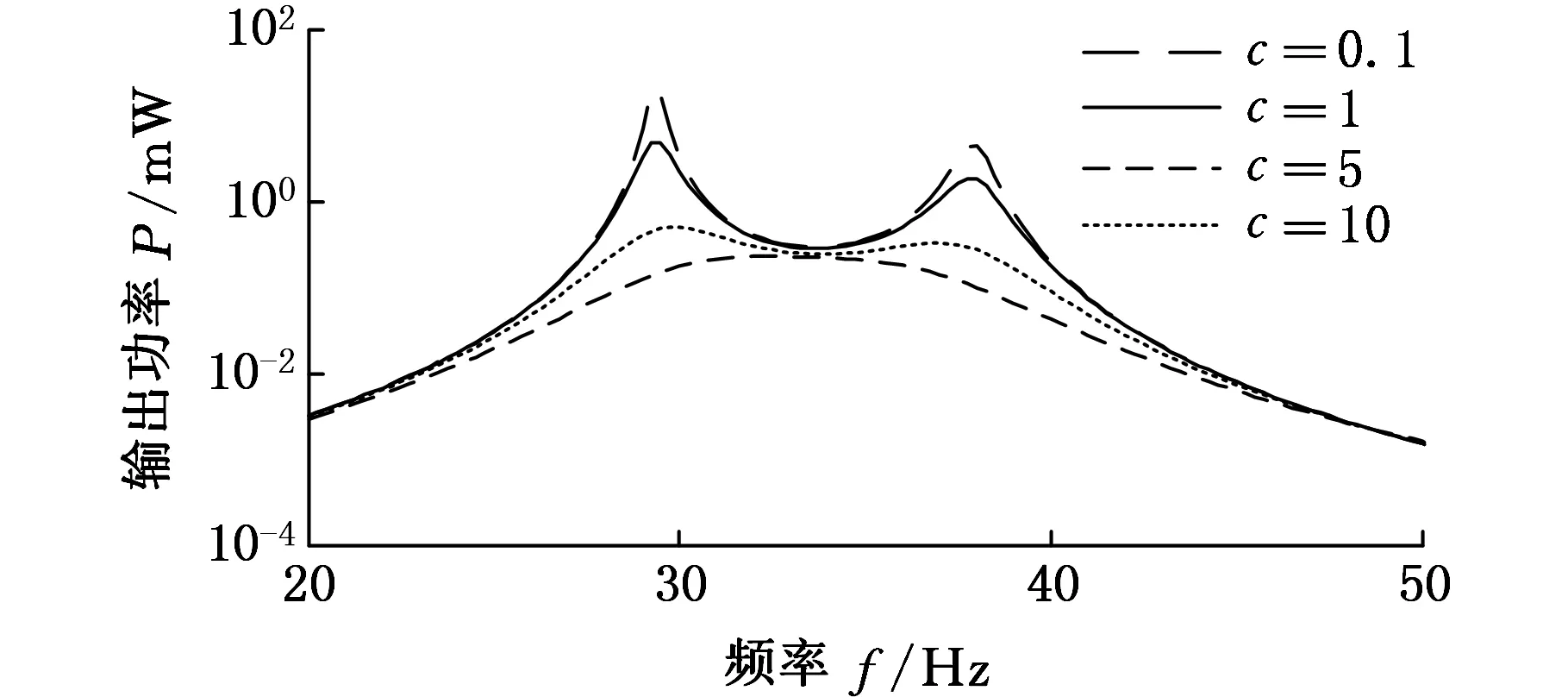
图5 不同阻尼比c下的输出功率的变化 (a=k，RL =1 kΩ)Fig.5 Output power of cantilever beam with different damping ratios c when ratios (a=k，RL =1 kΩ)

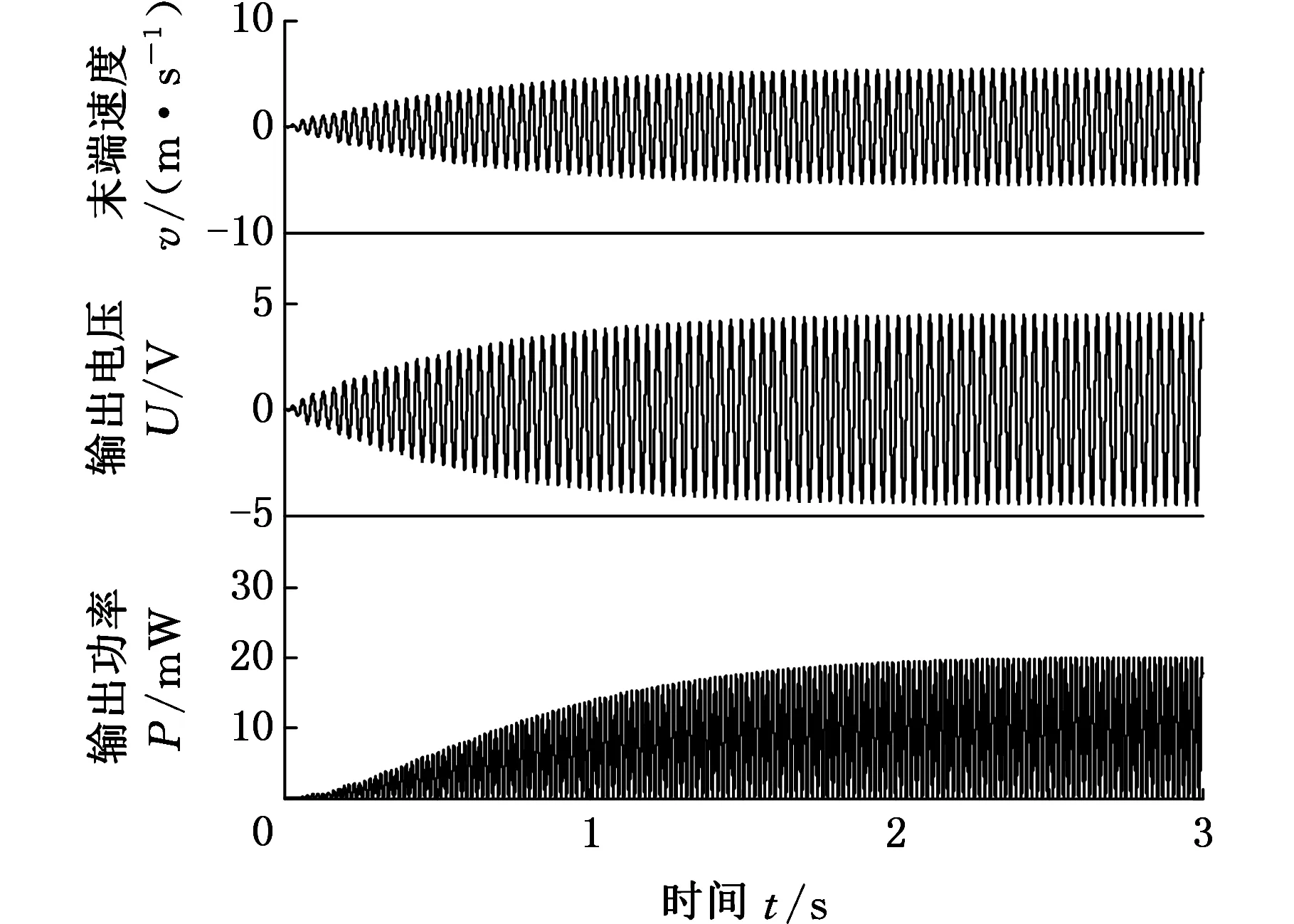
图6 TDOF压电能量采集器特性曲线 左峰点的时域响应(a=10，RL =1 kΩ)Fig.6 Time-domain response of left peak in performance curves for TDOF PVEH (a=10，RL =1 kΩ)

2.4 阻抗匹配优化

为了提高能量采集器的最大输出功率，负载电阻必须与能量采集器的阻抗相匹配。能量采集器的谐振频率的计算公式为

(22)

图7 短路谐振和开路谐振下 负载变化时的输出功率Fig.7 Output power under short circuit and open circuit resonant with different load resistance

图8 a=k=10时，匹配负载电阻下TDOF系统 和SDOF系统输出功率的比较Fig.8 Output power comparison of TDOF system with SDOF system when ratios a=k=10

短路谐振时，压电能量采集器的有效刚度Keff=Keq，开路谐振时，压电能量采集器的有效刚度Keff=Keq(1+d)。由式(22)可以计算出短路谐振频率fsc=33.64 Hz，开路谐振频率foc=34.25 Hz。图7所示为系统短路谐振和开路谐振状态下，能量采集器输出功率随负载电阻R的变化曲线，可以看出，能量采集器短路谐振和开路谐振时的最佳匹配电阻分别是112 kΩ和196 kΩ，对应的最大输出功率(单位加速度g激励条件下)分别为27.56 mW和27.4 mW。图8所示为最佳匹配负载电阻情况下，TDOF和SDOF能量采集器输出功率仿真结果，可以看出，TDOF能量采集器的最大输出功率比SDOF的最大输出功率高。另外，TDOF能量采集器的频带比SDOF能量采集器的频带宽，TDOF系统左右两峰之间的带宽为8.5 Hz，而SDOF系统的带宽为1 Hz。可见在相同的激励条件下，TDOF能量采集器扩宽了工作频带，提高了能量的采集效率和工作频带。

3 试验验证

研制的TDOF和SDOF原理样机如图9所示，其中，TDOF能量采集器的质量比a=10，刚度比k=15。图10所示为压电能量采集器实验测试系统。信号发生器产生的正弦交流信号经过内置功率放大器放大后，激励激振器和基座作正弦波振动；能量采集器和加速度传感器(型号：CD-210)通过高强度502胶并列黏结在基座上；基座振动加速度和TDOF能量采集器的悬臂梁末端位移分别经加速度传感器和电涡流传感器(型号：HZ-8500φ11)采集后送入动态信号分析仪分析后，再经过INV1601型信息采集软件输出到显示器；TDOF能量采集器的输出电压通过示波器显示。

1.SDOF PVEH 2.TDOF PVEH 3.加速度传感器图9 TDOF和SDOF原理样机Fig.9 Prototypes of TDOF and SDOF

1.信号发生器 2.动态与信号分析仪 3.基座 4.电涡流位移传感器 5.激振器 6.显示器 7.示波器图10 压电能量采集器实验测试系统Fig.10 Experimental setup of piezoelectric energy harvesters

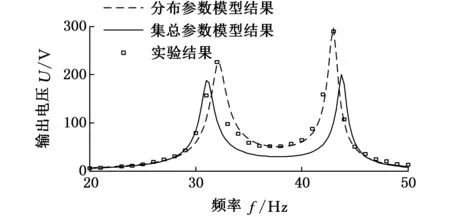
将提出的分布参数模型和集总参数模型[10]的数值分析结果与实验研究结果进行比对,图11、图12所示分别为负载电阻RL=112 kΩ，196 kΩ时的TDOF能量采集器输出电压与输出功率。从图11 、图12中可以看出，分布参数模型输出结果与试验测试结果具有更高的吻合度，验证了分布参数机电耦合模型的正确性。在RL=112 kΩ时，分布参数最大输出电压、输出功率(单位加速度g激励条件下)分别为207.7 V和385.1 mW，左右两峰之间的频率间距为10 Hz。在RL=196 kΩ时，分布参数最大输出电压、输出功率(单位加速度g激励条件下)下分别为289.6 V和395.7 mW，左右两峰之间的频率间距为11 Hz。可见，TDOF在负载完全匹配状态下，能量采集输出性能大大提高，系统机械振动能量损耗小，能量转换效率高。

(a)输出电压U随频率f的变化

(b)输出功率P随频率f的变化图11 输出电压、输出功率的试验与分布参数和 集总参数(a=10，k=15,RL=112 kΩ)Fig.11 Output voltage and output power comparison of experimental results with distributed parameter and lumped parameter results when ratios (a=10，k=15,RL=112 kΩ)

图13a所示为激励加速度0.65 m/s2、激励频率36 Hz下TDOF能量采集器的末端位移。图13b所示为相同激励条件下TDOF和SDOF能量采集器在RL=196 kΩ时测得的输出电压响应。可知，TDOF能量采集器的末端位移为140 μm，输出电压为3.48 V，SDOF能量采集器的输出电压为0.98 V，TDOF能量采集器输出电压是SDOF能量采集器输出电压的3.55倍，再一次说明TDOF能量采集器具有较好的能量采集输出能力。

(a)输出电压U随频率f的变化

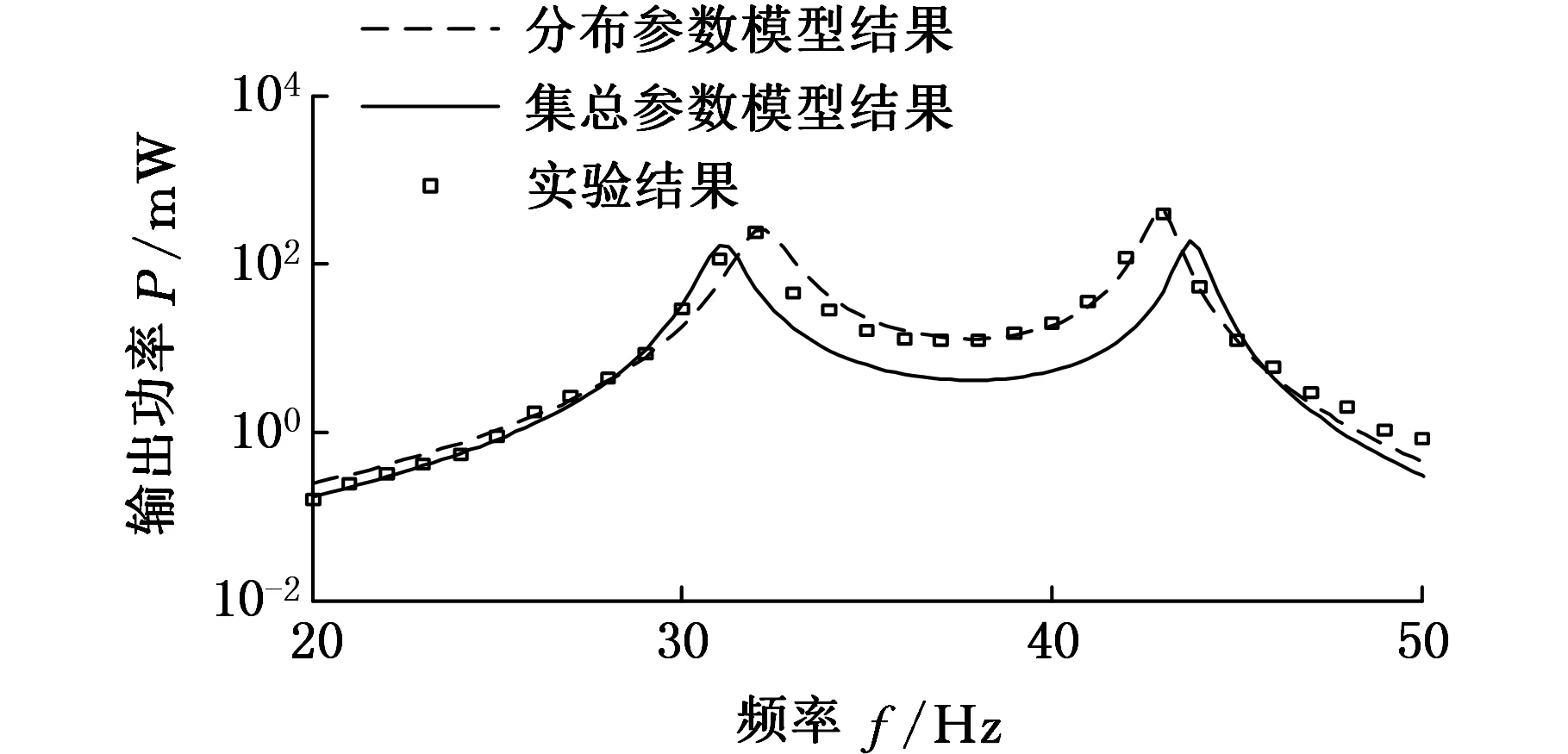
(b)输出功率P随频率f的变化图12 输出电压、输出功率的试验与分布参数和 集总参数(a=10，k=15,RL=196 kΩ)Fig.12 Output voltage and output power comparison of experimental results with distributed parameter and lumped parameter results when ratios (a=10，k=15,RL=196 kΩ)

(a)末端位移

(b)输出电压图13 TDOF采集器末端位移和 输出电压时域响应曲线界面 (a=10，k=15,RL=196 kΩ)Fig.13 History responses of tip displacement and output voltage of TDOF PVEH (a=10，k=15,RL=196 kΩ)

要说明的是，样机制作过程中，受悬臂梁和压电陶瓷的加工尺寸误差、黏结过程胶层厚度难以控制以及弹簧刚度测量误差等实际因素的影响，样机难以实现a=k，因此，实验研究中未对此情形加以验证，但这并不能否定a=k时，能量采集器具有上述良好的输出特性。

4 结论

(1)TDOF能量采集器在相同的激励条件下比SDOF能量采集器具有更宽的有效工作频带和更高的能量采集效率。

(2)仿真结果表明a=k时，增大质量比或刚度比和减小阻尼比可以提高能量采集器的末端振动速度、输出电压和输出功率，同时可以使输出特性曲线左右峰值间的频率间距减小，形成宽频带窗口。

(3)仿真和实验结果表明，在相同条件下，分布参数模型比集总参数模型具有更高的预测精度。在a=10，k=15，负载电阻RL=112 kΩ时，TDOF能量采集器最大输出电压、输出功率(单位加速度g激励条件下)分别为207.7 V和385.1 mW，左右两峰之间的频率间距为10 Hz。在RL=196 kΩ时，最大输出电压、输出功率(单位加速度g激励条件下)分别为289.6 V和395.7 mW，左右两峰之间的频率间距为11 Hz。

[1] 王光庆，鲍鹏，陆跃明，等. 复合L形宽频压电悬臂梁的建模与仿真[J]. 中国机械工程，2013，24(14)：1933-1938. WANG Guangqing， BAO Peng， LU Yueming， et al. Modeling and Simulation Analysis for a L-shaped Wideband Piezo-electric Cantilever Beam[J]. China Mechanical Engineering， 2013， 24(14)： 1933-1938.

[2] ERTURK A，INMAN D J. On Mechanical Modeling of Cantilevered Piezoelectric Vibration Energy Harvester[J]. Journal of Intelligent Materials Systems and Structures， 2008，19：1311-1325.

[3] ERTURK A，INMAN D J. A Distributed Parameter Electromechanical Model for Cantilevered Piezoelectric Energy Harvesters[J]. Journal of Vibration and Acoustics，2008，130：2-15.

[4] TANG X D，ZUO L. Enhanced Vibration Energy Harvesting Using Dual-Mass Systems[J]. Journal of Sound and Vibration，2011，330(21)：5199-5209.

[5] ALDRAIHEM O，BAZ A. Energy Harvester with a Dynamic Magnifier[J]. Intelligent Material Systems and Structures，2011，22(6)：521-530.

[6] MA P S，KIM J E，KIM Y Y. Power-amplifying Strategy in Vibration-powered Energy Harvesters[J]. Proc. of SPIE, 2010，7643：764300.

[7] WANG H Y，SHAN X B，XIE T. An Energy Harvester Combining a Piezoelectric Cantilever and a Single Degree of Freedom Elastic System[J]. Journal of Zhejiang University—Science A，2012，13(7)：526-537.

[8] 喻其炳，朱荣荣，李川. 多频响应的压电振动能量采集器的性能分析与测试[J]. 中国机械工程，2014，25(15)：2064-2069. YU Qibing，ZHU Rongrong，LI Chuan. Performance Analyses and Experiments of a Piezoelectric Vibration Energy Harvested with Multifrequency Response Capability[J]. China Mechanical Engineering，2014，25(15)：2064-2069.

[9] 王光庆，展永政，金文平，等. 一种宽频压电振动能量采集器的解析模型与试验研究[J]. 机械工程学报，2015，49(6)：198-207. WANG Guangqing，ZHAN Yongzhen，JIN Wenping，et al. Model and Experiments of a Broadband Piezoelectric Vibration Energy Harvester[J]. Journal of Mechanical Engineering，2015，49(6)：198-207.

[10] ERTURK A，INMAN D J. An Experimentally Validated Bimorph Cantilever Model for Piezoelectric Energy Harvesting from Base Excitations [J].Smart Materials and Structures，2009，18(2)：1-18.

(编辑 张 洋)

Distributed Parameter Model and Experiments of a Broadband Piezoelectric Vibration Energy Harvester

YANG Binqiang XU Wentan LU Guoli WANG Guangqing

School of Information and Electronic Engineering，Zhejiang Gongshang University，Hangzhou，310018

To solve self-power problem of wireless sensor network nodes, a broadband piezoelectric vibration energy harvester with an elastic supporter and amplifier was presented herein. Distributed parameter coupling electromechanical model of piezoelectric vibration energy harvester was established with Hamilton principle and Raleigh-Ritz method by considering the influences of cantilever tip mass. Effects of structural parameters (such as mass ratio, stiffness ratio, and damping ratio) on the vibration performance, the electric output performance of piezoelectric energy harvester were numerically analyzed. Prototype of piezoelectric energy harvester and experimental setup were developed. Some experiments were carried out to testify the validity of the proposed mathematical model. Research results show that the distributed parameter model may obtain higher precision than that of lumped parameter model.

piezoelectric energy harvester； two degrees of freedom； distributed parameter model； elastic amplifier； wide frequency band

2016-03-07

国家自然科学基金资助项目(51277165 )； 浙江省自然科学基金资助项目(LF15Y0001)

10.3969/j.issn.1004-132X.2017.02.001

杨斌强，男，1993年生。浙江工商大学信息与电子工程学院硕士研究生。主要研究方向为压电振动能量采集技术。徐文潭，男，1993年生。浙江工商大学信息与电子工程学院硕士研究生。陆国丽，女，1990年生。浙江工商大学信息与电子工程学院硕士研究生。王光庆(通信作者)，男，1975年生。浙江工商大学信息与电子工程学院教授。E-mail:kele76@163.com。

中国分类号：TH16；TH7