微纳米高折射率涂敷层对长周期光纤光栅传输谱特性的影响*

2017-02-07罗海梅刘祝华陈淑芳祝传传

传感技术学报 2017年1期

关键词：涂敷包层涂覆

王君,罗海梅*,刘祝华,谭海,陈淑芳,祝传传

(1.江西师范大学物理与通信电子学院,南昌 330022;2.东华理工大学信息工程学院,南昌 330013)

微纳米高折射率涂敷层对长周期光纤光栅传输谱特性的影响*

王君1,罗海梅1*,刘祝华1,谭海2,陈淑芳1,祝传传1

(1.江西师范大学物理与通信电子学院,南昌 330022;2.东华理工大学信息工程学院,南昌 330013)

基于模式耦合理论,通过求解给定参数的覆盖高折射率微纳米涂敷层长周期光纤光栅(LPFG)的频谱,分析了四层模型LPFG中微纳米高折射率涂敷层对其传输谱特性的影响。研究结果表明:通过设计涂覆层厚度、涂覆层折射率变化范围以及LPFG包层厚度等参数,包层模将进入高折射率微纳米涂敷层中进行传输,在LPFG传输谱出现模式迁移现象;随着涂覆层折射率的增大,谐振峰波长向短波长方向漂移;LPFG包层半径越小,谐振峰波长对涂覆层折射率变化的响应灵明度越高。

长周期光纤光栅;传输谱;高折射涂覆层;模式迁移

长周期光纤光栅(LPFG)是一种被广泛应用的模间干涉型光纤器件。大部分文献在研究LPFG的模式耦合理论时主要采用三层的阶跃折射率光纤模型,即考虑纤芯、包层和环境介质,其中环境介质的半径认为是无限大[1-7]。近年来,表面和表层微纳米薄膜工艺的发展和成熟使得在光纤光栅的表面沉积微纳米厚的高折射率涂敷层介质成为可能。在这种情况下,光纤包层和环境介质之间就多了一层微纳米厚度的薄层。当该薄层的折射率高于光纤包层折射率且厚度为某些特定值时,光纤光栅中的包层模模场重新分布,包层模依次从低阶向高阶迁移至微纳米涂层中进行传输同时光纤光栅的谐振峰波长产生一个显著的漂移,也就是所谓的模式迁移现象[8-12]。

本文求解了一种给定参数的四层模型LPFG的频谱,分析了在不同微纳米涂敷层厚度和折射率下,其谐振波长的偏移情况,讨论了光纤光栅包层厚度对其谐振峰漂移量的影响,为覆盖微纳米涂敷层LPFG器件的参数设计和高灵敏度传感应用研究提供理论依据。

1 四层模型LPFG的模式耦合理论

四层光纤模型如图1所示,光纤的纤芯、包层、微纳米涂覆层以及环境介质的半径分别为a1、a2、a3和无穷大;对应的折射率分别为n1、n2、n3和n4。

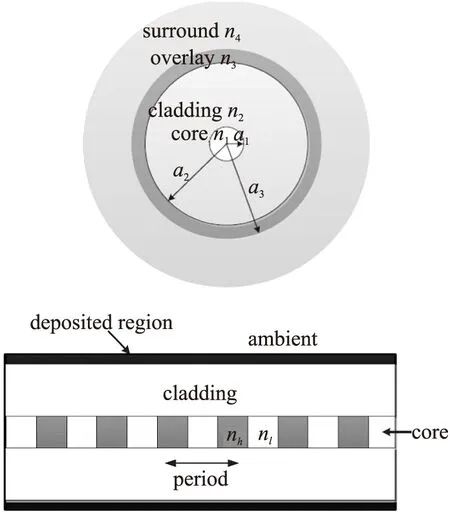
图1 四层光纤模型示意图

1.1 各包层模的有效折射率和传输常数

由于四层光纤模型的结构轴向对称,因此只需要考虑LP0m模式之间的耦合。包层模在这种四层结构中的横向电场分量的表达式为[13]:

(1)

式中:

式中:r为半径,Jv和Iv为v阶第1类和第2类贝塞尔函数,Yv和Kv为v阶第1类和第2类修正贝塞尔函数;n1、n2和n3分别为纤芯、包层和涂敷层的折射率,n4是环境折射率,neff为模式的有效折射率;a1和a2分别为光纤纤芯和包层的半径,a3-a2为涂敷层的厚度。另外,Ai为该电场分量在各种介质中的幅值,利用纤芯与包层,包层与涂敷层以及涂敷层与环境介质的3个边界条件便可以得出相应的Ai的解。这样,每个包层模的有效折射率便可以通过电场分量的连续性条件求得。

LPFG的模式耦合一般为纤芯基模与同向包层模之间的耦合,耦合常数的表达式为[14]:

(2)

式中:n1为纤芯折射率,R(r)是r的函数,表示模场径向的变化。

1.2 耦合系数和耦合常数

理想的单模光纤在没有受到扰动的时候,其纤芯和包层中的模式是正交的,没有耦合。在光纤中写入光栅便是在光纤纵向引入了折射率周期性微扰,模式间出现相互耦合,其横向耦合系数可表示为[15]:

(3)

式中:Ψ(r,φ)为LP模的横向场分量,Δε(r,φ,z)描述了折射率的扰动,假设各个模式的功率相等为P0。由于纵向耦合系数远远小于横向耦合系数而可以忽略不计,且折射率扰动很小一般与φ无关,因此我们可以做如下近似:

Δε(r,z)≈2ε0n0(r)Δn(r,z)

(4)

式中:ε0为真空介电常数,n0(r)为没有折射率干扰时光纤的折射率分布,Δn(r,z)表示折射率的变化,可用下式表示:

Δn(r,z)=p(r)σ(r)S(z)

(5)

式中:p(r)表示横向折射率扰动,一般仅存在于光纤的纤芯且为一个非零常数:

p(r)=p0·rect(r/a1)

(6)

式中:σ(r)为光栅的慢变包络,S(z)为径向折射率扰动因子。S(z)可以近似表示为:

S(z)=s0+s1cos((2π/Λ)z)

(7)

式中:Λ为光栅的周期。式中傅立叶级数的系数s0和s1依赖于光栅写入过程中的曝光强度。在后面的数值计算中,我们设定s0=s1=1。

经过以上的近似,模间耦合系数可表示为:

(8)

式中:ζvj,μk为耦合常数。LPFG的模式耦合一般为纤芯基模与同向包层模之间的耦合。因此,耦合常数的表达式为:

(9)

如前所述,n1为纤芯折射率,R(r)是r的函数,表示模场径向的变化。

1.3 谐振频率

普通的三层模型LPFG的谐振条件为[1-2]:

(10)

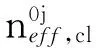
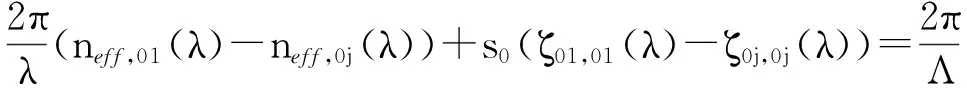
(11)

式中:ζ01,01和ζ0j,0j分别为自耦合系数以及纤芯模与第j阶包层模的耦合系数。另外,在第j阶包层模谐振波长处的基模透射率可表示为:

T0j=cos2(κ01,0j·L)

(12)

式中:L表示光栅的长度,κ01,0j为基模和第j阶包层模的耦合系数,可用下式表示:

(13)

2 数值仿真与分析

本文选取康宁公司生产的标准单模光纤为研究对象,相关参数为:纤芯折射率n1=1.449 21,包层折射率n2=1.444 03,纤芯半径a1=4.15μm,包层半径a2=62.5μm[16-17];其LPFG参数如下:LPFG的周期Λ=450μm,光栅区长度L=5mm,折射率调制满足σ(z)=s0=s1=1,光栅为均匀光栅。

2.1 高折射率微纳米涂敷层对LPFG模场分布的影响

在LPFG表面加上一层折射率高于光纤包层的涂敷层,随着该涂敷层厚度的增加,包层模的有效折射率也随之增大。当涂敷层的厚度达到一定值时,最低阶的包层模式会迁移到涂敷层中进行传输,此时,涂敷层中的能量猛然增加,这使得其他模式的有效折射率值重新调整。更高阶的包层模的有效折射率值变化为其前一阶的包层模的有效折射率值。于是,随着涂敷层厚度的进一步增加,在涂敷层沉积之前的LPFG的各包层模的有效折射率值被完全覆盖。涂敷层沉积之前的第8阶包层模式变成涂敷层沉积之后的第7阶包层模,而第7阶包层模变成第6阶包层模,以此类推。同样的情况也发生在LPFG的谐振峰波长的漂移上,随着涂敷层厚度的增大,该现象重复出现。这表明,随着涂敷层厚度的增加,越来越多的包层模迁移到涂敷层中进行传播,这样,不同包层模之间的能量出现重新分配。

设定纳米涂敷层的折射率n3=1.5,环境折射率为n4=1。图2为波长λ=1 550 nm的光在光纤中的纤芯基模(即LP01模)与前9个包层模(即LP02～LP10模)有效折射率随涂敷层厚度变化的曲线。LP02,LP03和LP04模式分别在涂敷层厚度达到约700 nm,2 600 nm和4 500 nm时进入微纳米涂敷层中进行传输。

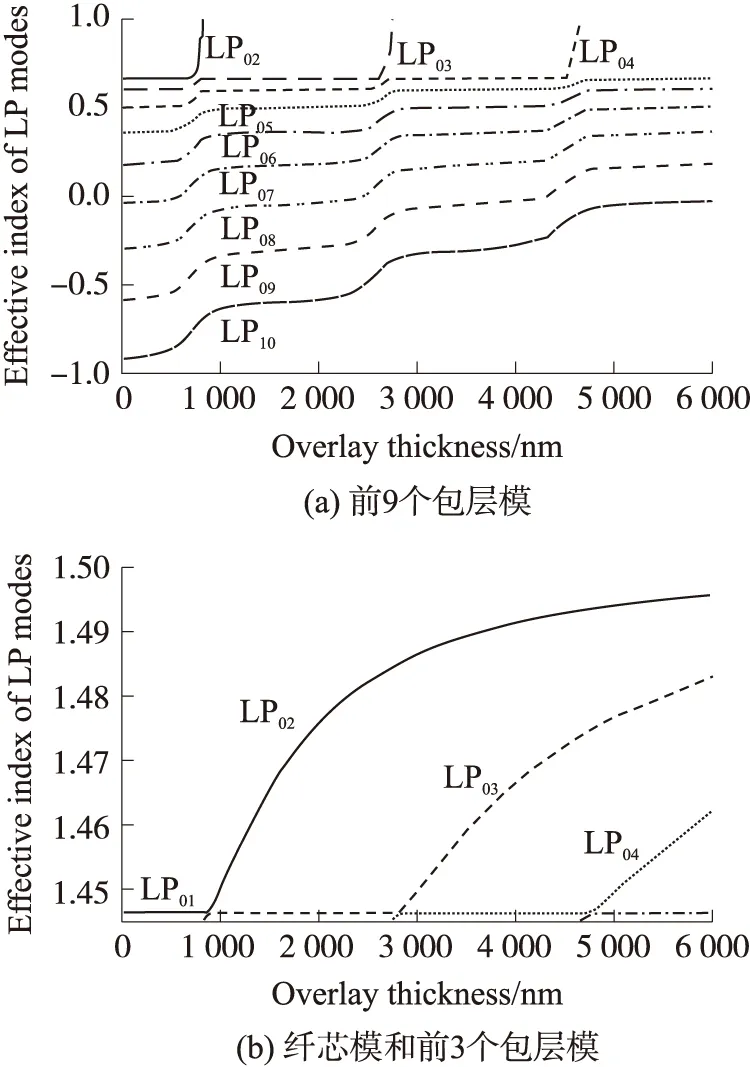
图2 不同高折射率层厚度下

每一阶包层模进入高折射率涂敷层进行传输时,更高一阶的包层模式便取代该模式之前在包层模中的位置,这一现象被称为模式迁移现象。图3为第5阶包层模在波长为1 550 nm,涂敷层厚度分别为0,970 nm和1 400 nm时的模场分布。其中,涂敷层为970 nm时,该模式正处于模式迁移状态中。从图中可以推断,随着涂敷层厚增大,LP05模的模场向LP04模的模场转变,也就是说,高阶模的模场向低阶模的模场转变。

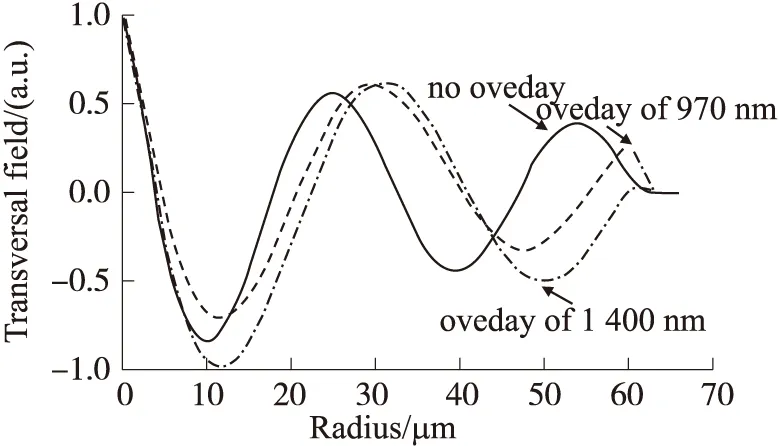
图3 相应的涂敷层厚度分别为0、970 nm和1 400 nm下的第5阶包层模的横向电场分布图

LPFG中各包层模的有效折射率的变化产生的直接结果就是谐振峰的漂移,即基模与第8阶包层模的谐振峰波长向涂敷层沉积之前的LPFG的基模与第7阶包层模的谐振峰波长漂移,而基模与第7阶包层模的谐振峰向之前基模与第6阶包层模的谐振峰波长漂移,以此类推。通过数值计算得出覆盖不同厚度的纳米涂敷层LPFG的频谱如图4所示。

图4 涂敷层折射率为1.5,环境折射率为1时的LPFG透射谱(实线、虚线和点线分别表示涂敷层厚度a3=0、400 nm和700 nm时的透射谱)

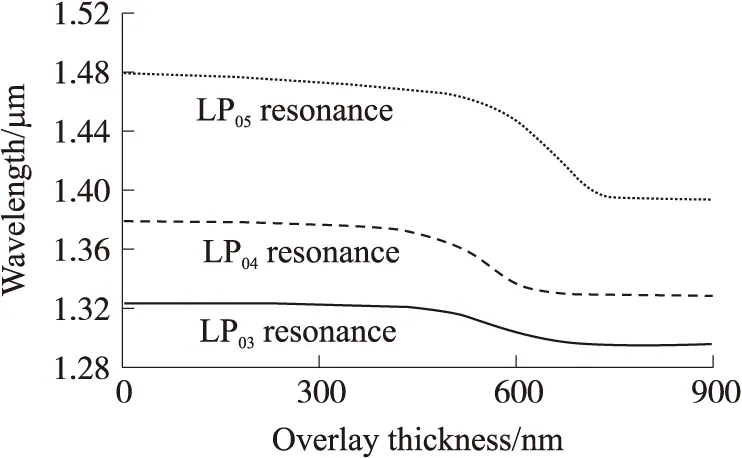
图5 基模与第3阶、第4阶和第5阶包层模谐振峰波长随涂覆层厚度的变化(涂覆层折射率为1.5,环境折射率为1)

图5反映了基模与第3阶、第4阶和第5阶包层模的谐振峰波长随涂覆层厚度变化的漂移情况。随着涂覆层厚度的增加,谐振峰向短波长的方向漂移,基模与高阶包层模谐振峰具有比基模与低阶包层模谐振峰更大的波长漂移量。

2.2 不同微纳米涂敷层折射率下的LPFG的频谱和大范围波长调谐

当涂覆层厚度为500 nm,环境折射率为1时,用数值方法分别计算得到不同涂覆层折射率下的LPFG的透射谱如图6所示。随着涂覆层折射率的增大,谐振峰波长向短波长方向漂移。

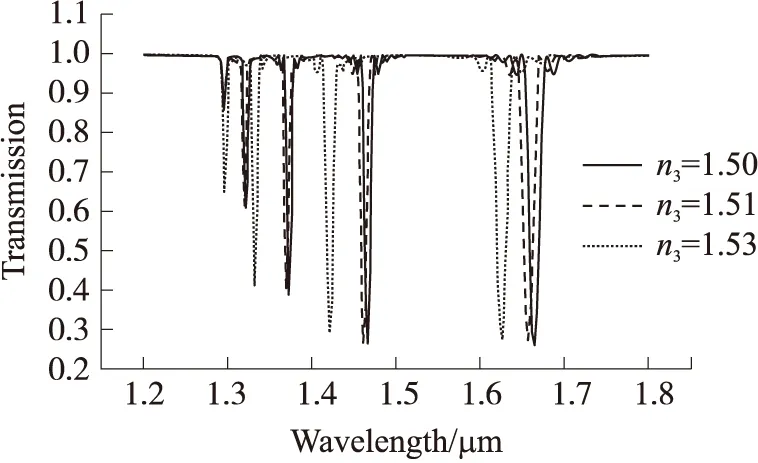
图6 涂敷层厚度为500n m的LPFG透射谱(实线、虚线和点线分别表示涂敷层折射率n3=1.5、1.51和1.53时的透射谱)

将数值计算得到的谐振峰波长随涂覆层折射率变化的情况用图7来表示。在涂覆层折射率从1.518逐渐增大到1.534的过程中,LPFG也出现了模式迁移的状况。在该模式迁移区域内,谐振峰波长随涂覆层折射率变化的漂移量远远大于该区域以外的谐振峰随涂覆层折射率变化的漂移量。因此,可以通过设计涂覆层厚度、涂覆层折射率以及环境折射率等参数,使LPFG的微纳米涂覆层折射率调谐的工作区域正好处于模式迁移区内,从而获得大范围的LPFG的涂覆层折射率调谐。

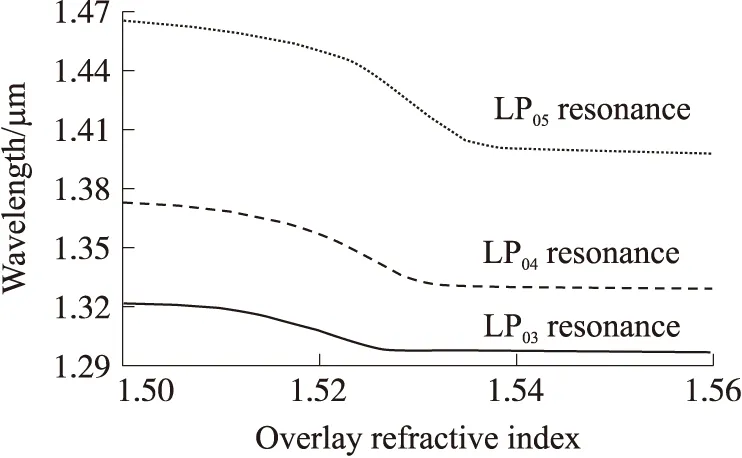
图7 基模与第3阶、第4阶和第5阶包层模的谐振峰波长随涂覆层折射率的变化(涂覆层厚度为500 μm,环境折射率为1)

2.3 LPFG的包层半径对谐振峰漂移量的影响

计算LPFG包层半径分别62.5 μm和40 μm时,不同涂覆层折射率下基模和第4阶包层模谐振峰波长漂移,如图8所示。

在环境同为空气且涂覆层厚度为500 nm的情况下,当选取内包层半径r3=62.5 μm时,随着涂覆层折射率从1.5变化到1.51,LP05模谐振峰波长从1 373.1 nm漂移到1 369.7 nm,漂移了3.4 nm;当包层半径r3=40 μm时,LP05模谐振峰波长从1 610.6 nm漂移到1 599.6 nm,漂移了10 nm;当包层半径r3=25 μm时,LP05模谐振峰波长从1 932.5 nm漂移到1 872.5 nm,漂移了60 nm。由此可见,可以通过减小LPFG包层半径的方法来增加谐振峰波长对涂覆层折射率的灵明度,从而扩大其调谐范围。

图8 LPFG包层半径分别为62.5 nm和40 nm以及25 nm时,同涂覆层折射率情况下LP05模的谐振峰波长漂移量对比

3 结论

本文基于四层光纤模型,研究了覆盖高折射率微纳米涂敷层的LPFG的包层模特性,同时对四层模型LPFG谐振波长和频谱特性进行了分析。结果表明,合理选择微纳米涂敷层的相关参数,LPFG频谱出现模式迁移现象;随着光纤光栅包层厚度的减小,基模与各包层模的谐振峰波长的漂移量越来越大;改变微纳米涂敷层折射率,包层模阶数越高的谐振峰的漂移量越大。该研究为高效率可调谐光纤器件以及高灵敏度传感光纤器件的设计和制备提供了理论依据。

[1] Liu T,Chen X,Yun D,et al. Tunable Magneto-Optical Wavelength Filter of Long-Period Fiber Grating with Magnetic Fluids[J]. Appl Phys Lett,2007,91(121116):1-3.

[2] Singh A,Rana S B,Singh M,et al. Study and Investigation of Long Period Grating as Refractive Index Sensor[J]. Optik,2014,125:1860-1863.

[3] Wang Y P,Xiao L M,Wang D N,et al. In-Fiber Polarizer Based on A Long-Period Fiber Grating Written on Photonic Crystal Fiber[J]. Opt Lett,2007,32(9):1035-1037.

[4] Singh A. Study of Modeling Aspects of Long Period Fiber Grating Using Three-Layer Fiber Geometry[J]. Photonic Sensors,2015,5(1):32-42.

[5] Jiang X,Li H,Yuan W. Simulation of the Effective Refractive Index of the Cladding Mode in LC-LPFG[J]. International Industrial Informatics and Computer Engineering Conference,2015:1305-1308.

[6] 张自嘉,许安涛. 薄包层长周期光纤光栅的折射率传感特性[J]. 传感技术学报,2009,22(8):1105-1108.

[7] 赵洪霞,程培红,鲍吉龙,等. 一种新型结构长周期光纤光栅光谱特性研究[J]. 传感技术学报,2014,27(6):743-1746.

[8] Luo H M,Wang C J,Wang X P,et al. The Effects of the Nanosized High Refractive Index Overlay on Tunable Long Period Gratings with Normal and Reduced Cladding Diameters[J]. Optik,2016,127:5230-5234.

[9] Zou F,Liu Y Q,Deng C,et al. Refractive Index Sensitivity of Nano-Film Coated Long-Period Fiber Gratings[J]. Opt Express,2015,23:1114-1124.

[10] Luo H M,Li X W,Li S G,et al. Analysis of Temperature-Dependent Mode Transition in Nanosized Liquid Crystal Layer-Coated Long Period Gratings[J]. Appl Opt,2009,48(25),F95-F100.

[11] Villar I D. Ultrahigh-Sensitivity Sensors Based on Thin-Film Coated Long Period Gratings with Reduced Diameter,in Transition Mode and Near the Dispersion Turning Point[J]. Opt Express,2015,23:8389-8398.

[12] Yang J. Sensitivity Enhanced Long-Period Grating Refractive Index Sensor with A Refractive Modified Cladding Layer[J]. Proc of SPIE,2005,5970(59701H):1-9.

[13] Cusano A. Mode Transition in Nano-Coated Long Period Fiber Gratings:Principle and Applications to Chemical Sensing[J]. Advanced Photonic Structures for Biological and Chemical Detection,2009:35-75.

[14] Anemogiannis E,Glytsis E N,Gaylord T K. Transmission Characteristics of Long-Period Gratings Having Arbitrary Azimutal/Radial Refractive Index Variation[J]. J Lightwave Technol,2003,21(3):218-227.

[15] Villar I D. Optimization of Sensitivity in Long Period Fiber Gratings with Overlay Deposition[J]. Opt Express,2005,13(1):56-69.

[16] 刘婷. 基于磁流体的长周期光纤光栅磁光可调谐光滤波器[D]. 上海:上海交通大学,2007.

[17] Cibula E,Donlagic D. In-Line Fabry-Pérot Refractive Index Sensor[J]. IEEE Photonics Technology Letters,2011,23(21):1609-1611.

Tuning Effects of Micro/Nano High Refractive Index Overlay on
the Transmission Spectra of Long Period Fiber Gratings*

WANGJun1,LUOHaimei1*,LIUZhuhua1,TanHai2,CHENShufang1,ZHUChuanchuan1

(1.College of Physics and Communication Electronics,Jiangxi Normal University,Nanchang 330022,China;2.School of Information and Engineer,East China University of Technology,Nanchang 330013,China)

Tuning effects of micro/nano high refractive index overlay on the transmission spectra of long period fiber gratings(LPFG)with given parameters are theoretically analyzed and numerically simulated by using coupled model theory. The results show that the phenomena of mode transition appear when the cladding mode entering the high refractive index overlay for transmission through properly designing the overlay thickness,overlay refractive index change range,and LPFG coating thickness. With the increase of the refractive index of the overlay,resonance peaks shift towards the shorter wavelength. The smaller the overlay radius,the higher the sensitivity of the resonance peaks in response to refractive index of the overlay.

LPFGs;transmission spectrum;high refractive index overlay;mode transition