浅谈高一物理“动态平衡”问题的解题思路

文 棋

(江苏省徐州高级中学 221000)

众所周知,牛顿运动定律是高中物理学科的重要规律，是历年高考物理试卷中考察的重点内容.而“平衡态”又是牛顿运动定律涉及的重要知识点，是考察学生知识与能力的重要抓手(以2017年江苏高考物理考试说明为例，第7个考点即 “共点力作用下物体的平衡”)，而“动态平衡”问题又是“平衡态”问题的“高难度部分”，如果学生能牢固地掌握“动态平衡”问题的解题思路(技巧)，那么他们就能掌握牛顿第一定律，而且也为以后牛顿第二定律的学习和研究打下坚实的基础.本人总结了解决此类问题的三种经典方法，供大家学习参考.

1.“动态平衡”问题的实质：是指物体(系统)在三个力作用下，不是保持某一种“状态”不变(例如静止或匀速直线运动),而是其涉及的某些物理量(例如角度，长度等)在不断变化中，但每个“态”均为“平衡态”，即F合=0.

2.动态平衡问题的“关键词”：这一类问题的语言表述中，往往带有“缓慢”、“慢慢等词语.

3.处理方法

(1)公式法：即根据三个力作用下F合=0，利用正交分解法(也可以利用力的合成、力的分解的方法)列出平衡方程ΣFx=0，ΣFy=0，根据三角函数的知识，判断所求力的大小变化.

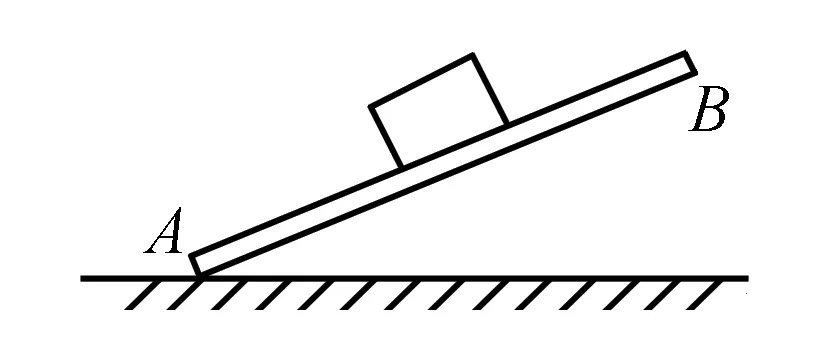
图1

例1 如图1所示,一物块质量为m放置在斜面上，斜面倾角α由0缓慢增至某一角度，整个过程物块与斜面保持相对静止，问物块受到的f静与N大小如何变化？

解建立如图2所示的坐标轴，由“平衡态”可知

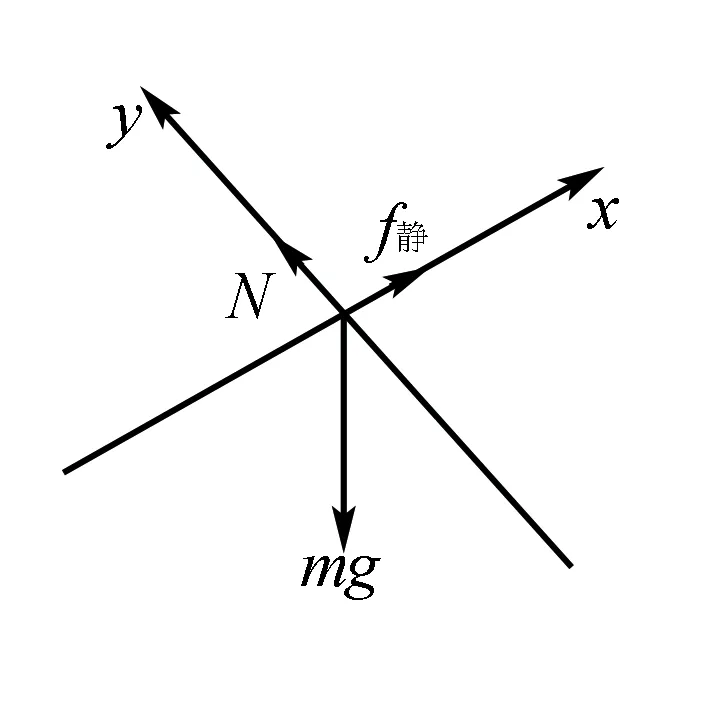
图2

X：f静=mgsinα;Y：N=mgcosα

∵α↑ ，则sinα↑，cosα↓ ，故f静↑，N↓，得解.

总结：此种方法适用于特殊的平行四边形或三角形(例如：本例f静与N始终垂直，构成直角三角形)我们根据三角函数的知识，得到所求力的表达式(故称公式法)，其大小变化一目了然.

(2)作图法：即根据力的平行四边形定则(或三角形定则)，作出“力”对应的不同三角形，根据边长的长短变化，判断力的大小变化.

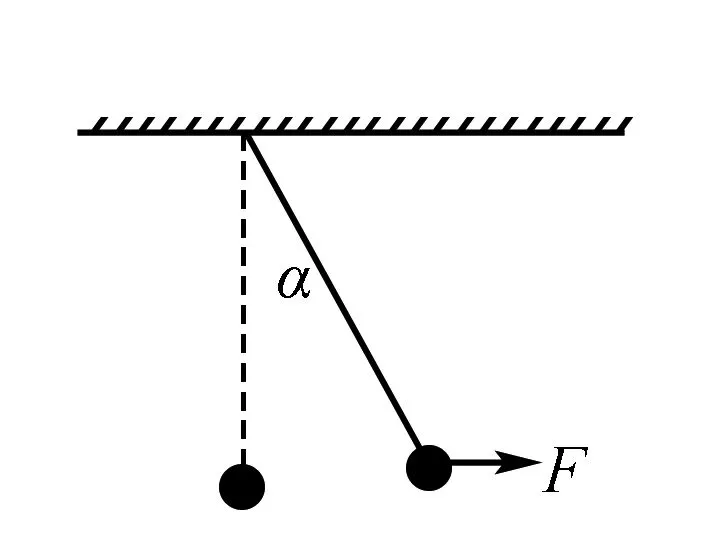
图3

例2 如图3所示,不可伸长的轻质细线一端拴着质量为m的可视为质点的小球，另一端系于天花板上，现在对小球施加一个水平向右的力F，使小球缓慢移动直至细线与竖直方向夹α角，问该过程中水平力与细线上的弹力大小怎么变？

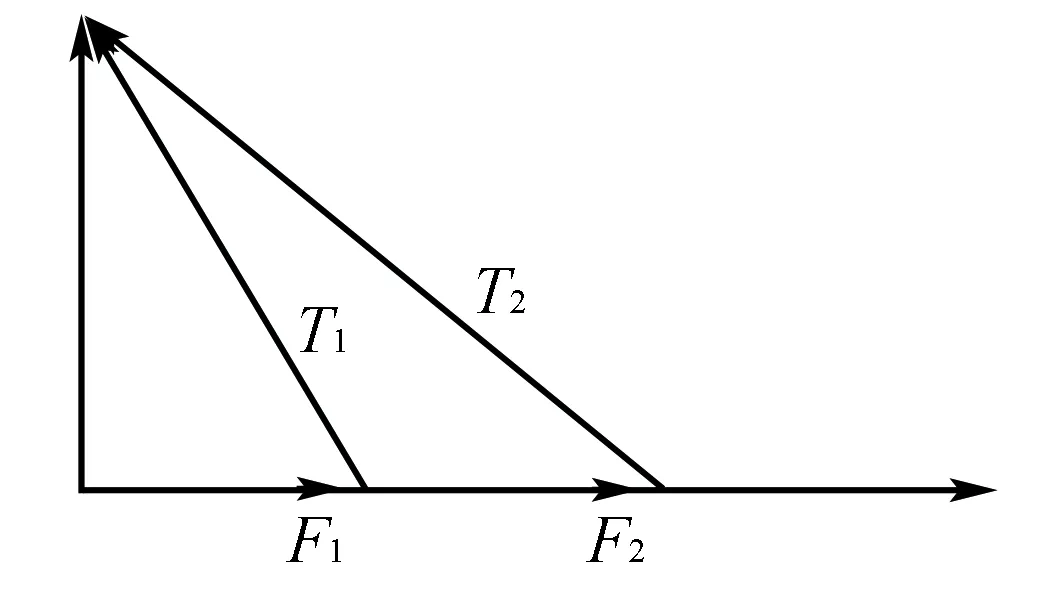
图4

解根据F合=0，则任意两个力的合力与第三个力为一对平衡力的规律可知，拉力T与水平力F合力大小为mg，方向竖直向上，且水平拉力方向不变，如图4：由力的三角形定则可得：因为细线与竖直方向的夹角变大，由图4两个三角形可知F↑ ，T↑ ， 得解.

总结：此种方法适用于三个力中有一个恒力(比如重力)，且另外两个力其中之一方向不变(比如水平拉力)，我们根据力的三角形定则做出不同三角形，通过边长变化判断其大小变化.此方法快捷，但不能量化结果.

反思：上述例2(作图法)中，由于F与G始终垂直，所以存在特殊的平行四边形(三角形)，可用公式法求解.

解建坐标轴，如图5.

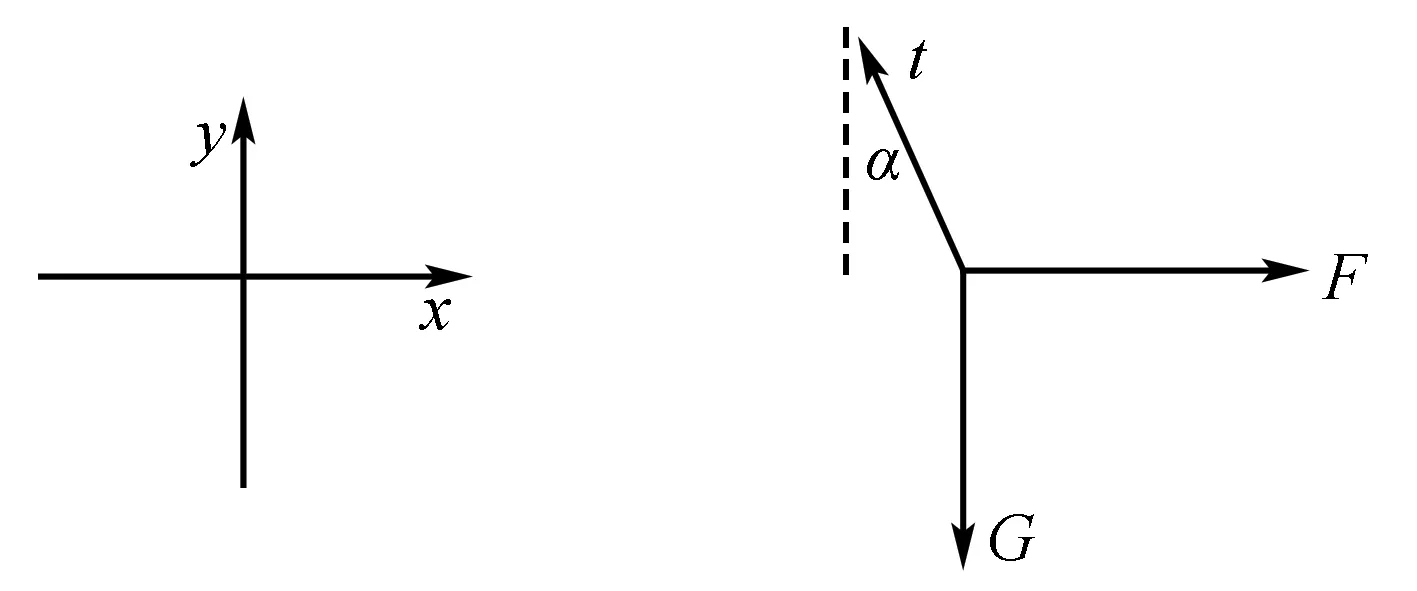
图5 图6

列方程由图6可得X：Tsinα=F；Y：Tcosα=mg，则T=mg/cosα，

F=mgtanα，∵α↑ ，则tanα↑，cosα↓ ，故T↑,F↑，得解.

拓展：请问例1(公式法)可以用作图法吗？分析条件，可知例1中，f静与N方向不断变化，乍一看不满足“方法二”的条件，但是由于N与f静方向时刻垂直，存在特殊的平行四边形，故作图法未尝不可！

解如图7所示，由于斜面倾角变大，故应从甲图看到乙图(两个图中对应mg的线段长短应保证不变)，由乙图可知，N↓，f静↑，得解.

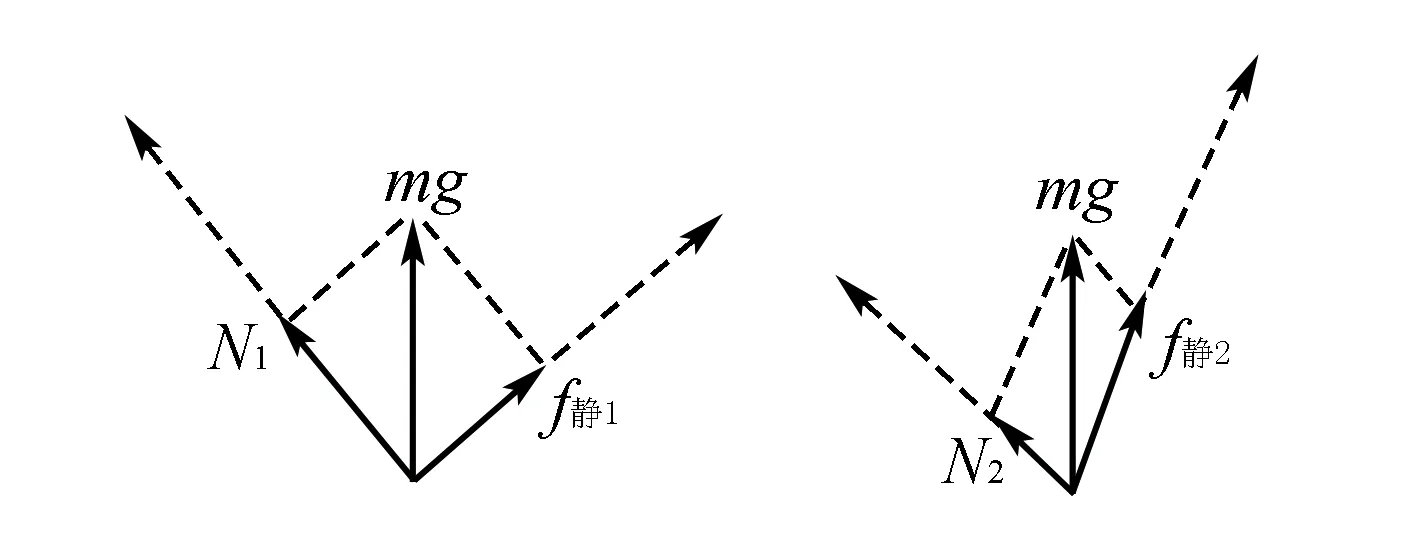
甲 乙图7

3.相似法：即根据力的“三角形”定则，作出力的对应三角形，设法找到题目中“真实”的几何三角形，通过两个三角形相似对应边成比例的规律，判断力的大小变化.

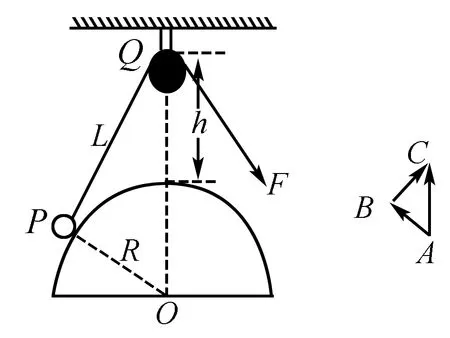
图8 图9

例3 如图8所示，光滑的半球形装置，球心O正上方悬挂一光滑定滑轮，不可伸长的细线一端栓着质量为m的小球(视为质点)，另一端通过定滑轮，用力F将小球沿球面底部缓慢移至球面最高处，在此过程中，球面的支持力与细线的拉力大小如何变化？

解如图9所示：根据三角形定则可作出力对应的三角形ABC，与装置中的三角形OPQ相似，经分析OQ长度不变，对应力mg大小不变，即相似比为定值，则虽然支持力AB方向不断在变，但对应的相似三角形OP边长度始终为球半径(不变)故支持力大小不变；又因为PQ边逐渐变短，则对应的拉力逐渐变小，得解.

总结：上例中我们发现三个力中有一个力是恒力，但另外两个力方向不断变化且不构成特殊角，不能用“公式法”和“作图法”，只有“相似法”可以解决.也就是说，“相似法”是条件最“普通”的.

那么我们思考：例1、例2可否能用“最普遍”的相似法解决问题呢？答案是肯定的.

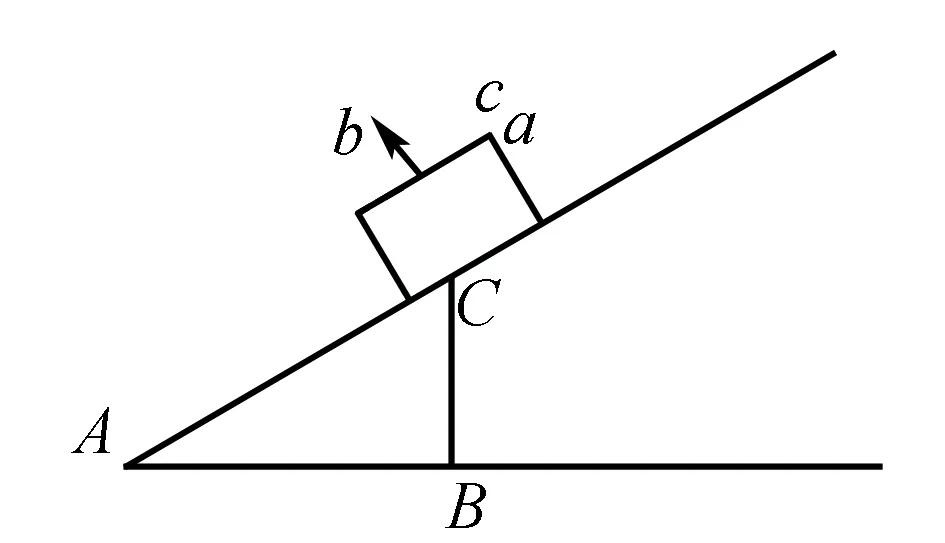
图10

再探例1如图10我们发现，对应三个力的三角形abc与图中几何三角形ABC相似，AC长度不变，对应ac边即G大小不变，则相似比不变，随着斜面倾角不断增大 ，BC边(物体到地面的垂线段)变大，则f静↑ ，AB边变小，则N↓，得解.

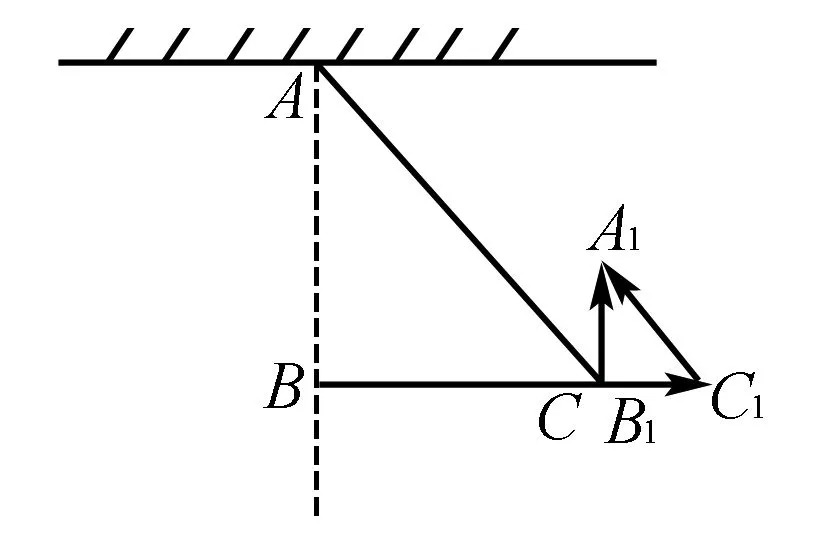
图11

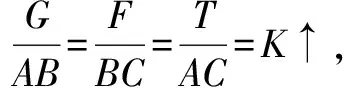
由此可见，一道“动态平衡”的题目解决方法往往不止一种，大家可以试一试，用三种方法解决下列例题.

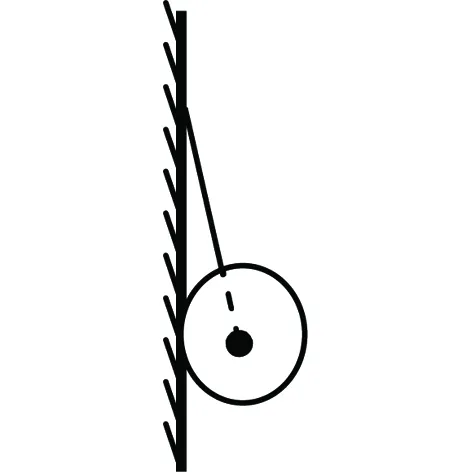
图12

例4 如图12所示，重为G的小球用细绳系在竖直的墙壁上，细线延长线通过球心，若将细绳缓慢增长,问墙壁对小球的支持力及细绳对球的拉力的大小变化情况？(公式法与作图法略)

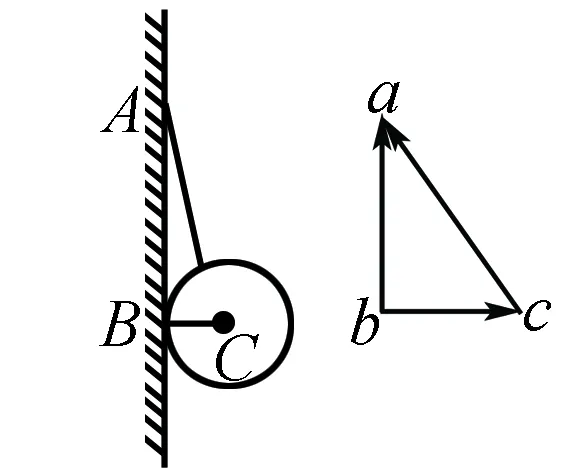
甲 乙图13

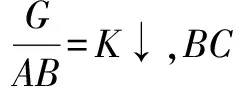
综上，希望同学们能够熟练地掌握“动态平衡”问题三种解题方法，牢固掌握牛顿第一定律，为今后更好地学习物理打下基础，同时也希望广大教师在教学过程中，多反思多总结，能更高效地使学生掌握物理知识，帮助学生顺利通过思维的“瓶颈”.

[1]孙国臣. 高中物理教学中学生的解题能力培养研究[J].中国职工教育，2014(10):179-179.