概率问题的多解和慎答
2017-02-06孟方明
孟方明
(浙江省春晖中学 312353)
对于概率问题,一方面若从不同的角度来寻求概率模型或审视样本空间,往往可以得到不同的解法,体现出思维的灵活性和广阔性;另一方面,由于概率问题独特的抽象性、不确定性等特点,学生较难用解决确定性数学问题的思维模式应对“活”的概率问题,导致错误频发.在概率的教学过程中,必须重视对概率问题的多解和慎答.
一、多解
1.纳入不同概型
同一概率问题,对事件性质特征的理解因视角不同而可纳入不同概型,只要方法正确,结论是一致的.
例1 将一颗质地均匀的骰子先后抛掷3次,求至少出现一次6点向上的概率.
解法1 由于骰子是均匀的,因此将它抛掷3次,每次出现哪一点向上都是等可能的,故可纳入等可能概型,显然card(I)=63=216.
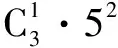

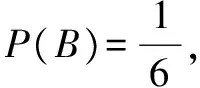

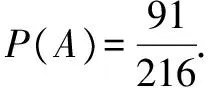
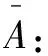
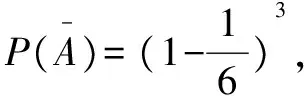
2.选用不同样本空间
古典概型是概率学习中的重点,它具有两个特征:试验结果的有限性和每一个试验结果出现的等可能性.同一概率问题,在确定基本事件(基本事件的全体称为样本空间)时,可以按不同的标准有不同的解释,只要试验结果满足上述两个特征,结论是一致的.
例2 已知盒中装有3只螺口与7只卡口灯泡,这些灯泡的外形和功率都相同,且灯口向下放着,现需要一只卡口灯泡使用,电工师傅每次从中任取一只并不放回,求他直到第3次才取得卡口灯泡的概率.

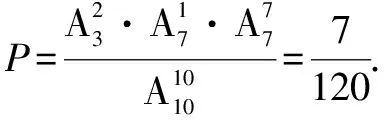
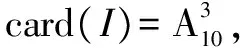
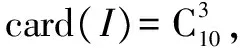
二、 慎答
1.错解概念
概率中的概念比较抽象,有些相互之间还容易引起混淆,如互斥与独立,学生初次学习概率,由于对它们理解不透彻,且学习中往往只重视公式的死记硬背,忽视概念的理解掌握,从而在事件概念的定位上张冠李戴、错态百出.
例3 一台仪器配有A、B两套通路,只要其中一套通路通畅,仪器就能正常工作.A套由2个部件组成,B套由3个部件组成,只要其中有一个部件出现故障,这套通路就不能正常工作.如果在某段时间内每个部件不出现故障的概率都是p,试求在这段时间内仪器能正常工作的概率.
错解某段时间内A、B两套通路能正常工作的概率分别为P(A)=p2,P(B)=p3,由题意,A、B至少有一套正常工作,仪器就能工作,故在这段时间内仪器能正常工作的概率是P(A+B)=P(A)+P(B)=p2+p3.
析与解根据题意,A、B两套通路正常工作是相互独立的两个事件,上面所用公式是互斥事件有一个发生的概率加法公式,误把独立当成了互斥.互斥和独立是两种截然不同的概率关系,二者针对问题的角度不同,把互斥事件的概率公式套用在求独立事件的概率上是错误的. “A、B至少有一套能正常工作”的对立事件是“A、B都不能正常工作”,A不能正常工作的概率是1-p2,B不能正常工作的概率是1-p3,∴A、B都不能正常工作的概率是(1-p2)(1-p3),从而所求概率等于1-(1-p2)(1-p3)=p2+p3-p5.也可将“A、B至少有一套能正常工作”分解为三个互斥事件,利用概率加法公式,求得同一结果.
2.误解题意
由于概率的产生、建立和发展与生活实际密切相连,而生活中的问题,其条件和背景千差万别,一般没有固定的法则和套路.因此审题是解答概率问题中非常重要的一环.审题稍有偏差,极有可能误解题意,导致错解.
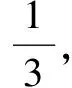
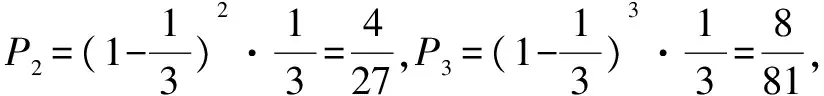
析与解错解中认为汽车从东站至西站非得遇到红灯不可,事实上,四岗都遇到绿灯也应视为是满足题意的.我们从对立事件的角度来解释,显然对立事件包括两种情况:在遇到红灯前通过0岗或通过1岗,概率
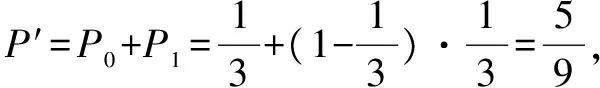
3.曲解公式
公式是概念的外在表现形式,选择公式首先需要正确理解概念,必须注意所选公式的适用前提、切实理解公式的内涵实质.如果只是单纯地记住公式外形,就会造成曲解公式,从而致错.
例5 甲、乙两人参加普法知识竞答,共有10个不同的题目,其中选择题6个,填空题4个,甲、乙依次各抽一题.
(Ⅰ)甲抽到选择题、乙抽到填空题的概率是多少?
(Ⅱ)甲、乙两人中至少有一人抽到选择题的概率是多少?
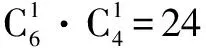
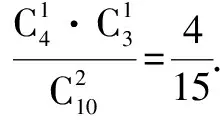
[1]严海平.求解概率题常见误区之浅析[J].中学数学研究,2006(7):38-40.
[2]谢鹏作.在困扰时吃透概念,从多解中厘清头绪[J].数学通讯,2014(7):22-24.
