小议一个数列不等式的放缩问题

曹卫民

(江苏省南通市通州区金沙中学 226300)

数列不等式是中学数学的难点，对于大多数学生而言，涉及到不等式放缩的问题难以入手，这主要因素是放缩的灵活度非常高，而且有些问题还需要对精度有较高的要求，因此成为学生的难点．本文首先从一到典型的多解型放缩问题出发，谈一谈放缩的基本技巧．

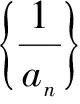
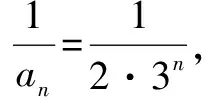
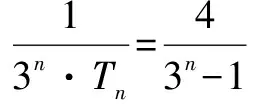
这是最为直接、简洁的放缩证明．这个证明中，每一项都较为合理地放缩成等比数列中的对应项，需要指出的是这种放缩方向性明确，而且放缩的基本数值也较为明确，只要进行简单的前几项尝试就可以得到，这是本题的常规思路之一——等比导向．

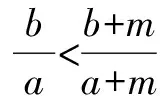
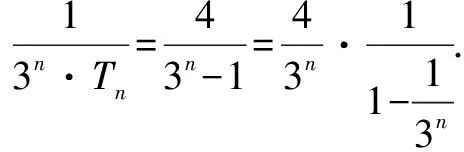
从最后的放缩形态来看，函数视角的放缩与思考1等比角度放缩如出一辙，有着异曲同工之妙．

小结从数列放缩的上述不同思考来看，这些基本放缩的方式在技巧性上并不是要求过高，是属于学生可以理解和掌握的层面，可以这么进行总结：一般来说：放缩的主导思路在于如何利用通项结构，主要从裂项、留项、已掌握的不等式运用等视角切入思考，这样的方式是放缩的常见技能．

演变有兴趣的读者可以从下列类似问题中获得上述思考的进一步验证和思考：

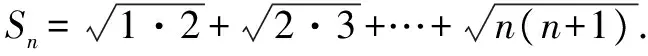
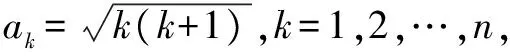
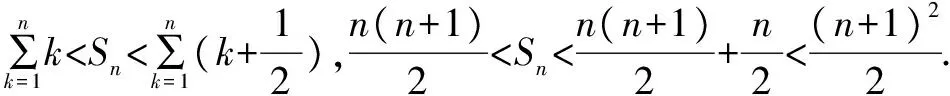
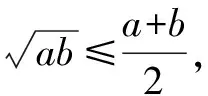
总之，从一个典型的问题出发去思考数列不等式常使用的手段，并加以归纳和思考、总结，对于我们进一步掌控数列不等式的放缩有重要的指导作用，数列不等式问题的放缩并无定法，但存在较为合理的解题思想，继续研究这些思想才能将放缩掌握得更为合理．

[1]王超.不等式中的常用经典不等式[J].中学数学教学,2015(6).