铯喷泉钟冷原子碰撞频移的差分法测量研究

2017-02-05林睿王心亮刘丹丹管勇张辉陈江余凤翔施俊如阮军张首刚

时间频率学报 2017年4期

林睿，王心亮，刘丹丹，管勇，张辉，陈江，余凤翔，施俊如，阮军，张首刚,4

LIN Rui1, 2, 3, WANG Xin-liang1, 2, 3, LIU Dan-dan1, 2, 3, GUAN Yong1, 2, 3, ZHANG Hui1, 2, CHEN Jiang1,2,3, YU Feng-xiang1,2,3, SHI Jun-ru1,2, RUAN Jun1,2, ZHANG Shou-gang1,2,4

铯喷泉钟冷原子碰撞频移的差分法测量研究

林睿1,2,3，王心亮1,2,3，刘丹丹1,2,3，管勇1,2,3，张辉1,2，陈江1,2,3，余凤翔1,2,3，施俊如1,2，阮军1,2，张首刚1,2,4

（1. 中国科学院国家授时中心，西安 710600； 2. 中国科学院时间频率基准重点实验室，西安 710600； 3.中国科学院大学，北京，100049； 4. 中国科学院大学天文与空间科学学院，北京 100049）

铯原子喷泉钟作为频率基准标校其他原子钟。冷原子碰撞频移是影响铯原子喷泉钟频率不确定度的主要因素之一。本文从理论上分析了基于原子数的差分测量法中各项参数在测量碰撞频移中的影响，研究表明：冷原子碰撞频移测量的统计不确定度主要取决于喷泉钟运行时高低原子数密度频差的阿伦方差，其系统不确定度取决于原子数的涨落、高低原子数密度之间的非线性密度比。应用该方法测量了铯原子喷泉钟NTSC-F1的碰撞频移，获得测量的冷原子碰撞频移的平均值为4.0×10-15，其测量的统计不确定度（A类）为3.2×10-15（=32768s）；其系统不确定度（B类）为6.5×10-16。

铯原子喷泉钟；频率不确定度；冷原子碰撞频移；差分测量法

0 引言

铯原子喷泉钟作为复现国际单位（SI）“秒”定义的频率基准，自1995年由法国LNE-SYRTE的Clairon小组首先实现以来[1]，已有多台成功运行的铯原子喷泉钟，其频率不确定度已优于3×10-16[2]。现在全世界有14台铯原子喷泉钟已经参与了国际原子时（TAI）的校标[3]，并被广泛应用于守时和基础物理等需要高精度时间的领域[4]。

铯原子喷泉钟的工作介质是温度为µK量级的冷原子，在此温度下，铯原子之间的碰撞表现出显著的量子效应：发生碰撞的两个铯原子的核外价电子的自旋状态发生交换，引起了铯原子的超精细磁子能级的移动，从而导致铯原子超精细磁子能级跃迁频率的变化。冷原子碰撞频移是影响铯原子喷泉钟频率不确定度的最主要因素之一。本文基于原子数的差分法测量了铯原子喷泉钟NTSC-F1的冷原子碰撞频移，给出了其测量的不确定度。

1 冷原子碰撞频移的差分测量法

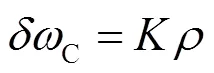
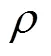
依据式（2）和文献[12]，相应的冷原子碰撞频移为

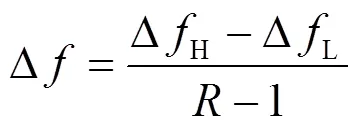
碰撞频移的测量不确定度可表示为

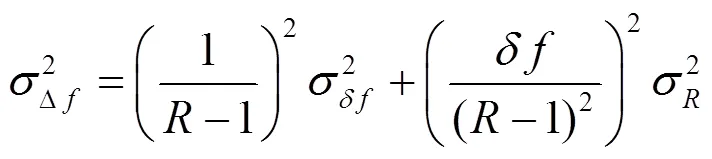
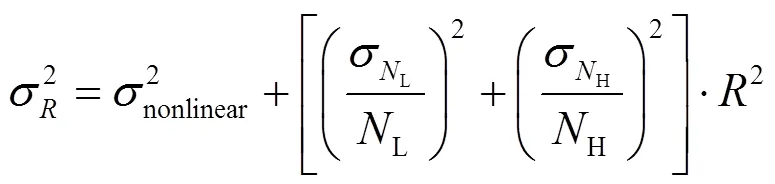
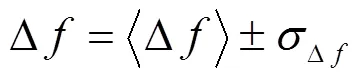
2 冷原子碰撞频移测量实验

2.1 高、低密度冷原子团原子数目的测量

依据式（1），（2）及（3），在铯原子喷泉钟NTSC-F1系统的基础上进行碰撞频移的测量，首先应确定好交替上抛的冷原子团的原子数比值。这就需要在铯原子喷泉钟运行的过程中改变上抛的原子数目。本文采用在选态阶段通过改变选态腔馈入的微波的功率实现原子数目的改变[14]。通过选态实验确定出产生原子数比为2的高、低原子数密度的微波功率，并给出在相应的微波功率作用下获得的高、低原子数密度的比值及其稳定度如图1所示。其中图1（a）反映了高、低原子数比值随时间的变化，可以看到在测量的绝大多数时间内（3000～10000s），这个比值大致均匀地分布在数值2附近，其均值为1.9534。比值的起伏反映了测量过程中冷原子团的原子数目随时间的变化，引起这种变化可能影响因素有：俘获冷原子时某些工作参数随时间的变化以及探测光学系统和电路系统随环境的变化等。图1（b）所示为原子数比值随喷泉钟运行时间的稳定度，可以看到在经过4 000个周期的测量（先运行200个高原子数密度的喷泉周期，再运行200个低原子数密度的喷泉周期，之后如前循环往复的测量），比值的稳定度已达4×10-5量级。

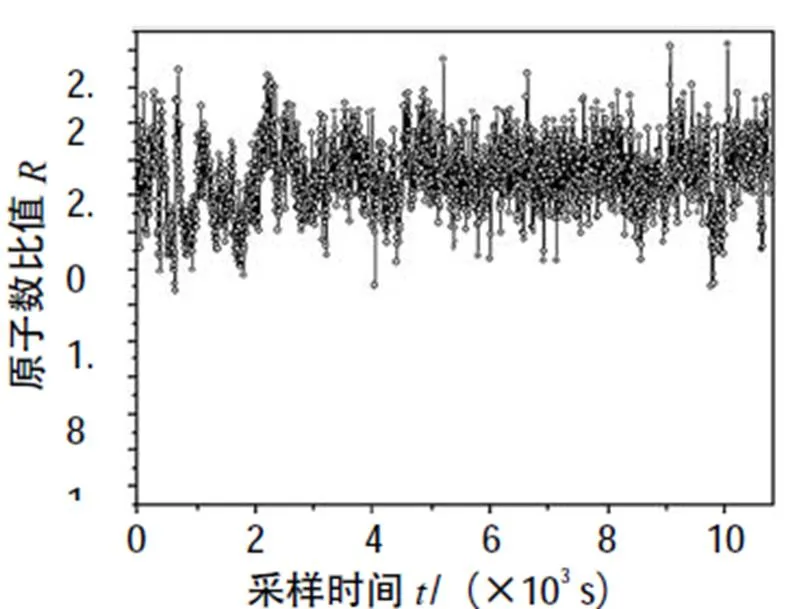
（a）高、低密度冷原子团的原子数比值的时间变化

（b）高、低密度冷原子团的原子数目比值的稳定度

图1 高、低密度冷原子团的原子数的比值

我们也对测量到的上抛冷原子的高、低原子数及其比值进行了统计分析，其统计特性由表1所示。在表1中可以看到当周期性交替馈入高密度原子团和低密度原子团的选态微波功率时，所产生的高、低原子数密度的原子团的原子数比值为1.953 4±0.094 04，符合按照微波功率所确定的原子数目比值＝2的要求，可以在此基础上进行冷原子碰撞频移测量的实验。

表1 高、低密度冷原子团的原子数及其比值的测量数据分析

2.2 冷原子碰撞频移的测量

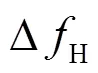
图2 铯喷泉钟在高、低密度冷原子团交替运行下与氢钟H296比对5d的Allan方差

表2 上抛高、低原子数密度的冷原子团在闭环锁定时的频差数据的统计结果 Hz

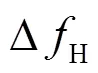
至此，本次测量所得到NTSC-F1铯喷泉钟的冷原子碰撞频移可表示为表3。

表3 NTSC-F1冷原子碰撞频移测量结果

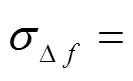
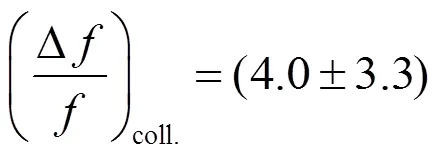
3 结论

本文在冷原子碰撞频移理论的基础上针对差分法分析了其测量的不确定度。在此基础上对铯原子喷泉钟的冷原子碰撞频移进行了初步的测量，获得如下的结果：NTSC-F1铯原子喷泉钟冷原子碰撞频移的平均值为4.0×10-15，其统计不确定度（A类）为3.2×10-15（＝32768s），系统不确定度（B类）为6.5×10-16。

本次测量为铯原子喷泉钟的冷原子碰撞频移的初步测量，高、低密度冷原子团的体积比、平均原子数密度与探测到的原子数存在非线性关系以及选态微波脉冲对冷原子碰撞系数的影响等因素所带来的非线性B类不确定度没有能很好地测量和估计，这将是下阶段提高铯原子喷泉钟性能的重要研究方向。

[1] CLAIRON A, LAURENT P, SANTARELLI G, et al. A cesium fountain frequency standard: preliminary results[J]. IEEE Transactions on Instrumentation and Measurement, 1995, 42(2): 128-131.

[2] ＲUAN Jun, WANG Xin-liang, LIU Dan-dan, et al. Progress of the NTSC-F1 primary frequency standard[J]. Instrumentation, 2015, 2(4): 16-27.

[3] FANG Fang, LI Ming-shou, LIN Ping-wei, et al. NIM5 Cs fountain clock and its evaluation[J]. Metrologia, 2015, 52(4): 454-468.

[4] 阮军, 王叶兵, 常宏, 等. 时间频率基准装置的研制现状[J]. 物理学报, 2015, 64(16): 160308-1.

[5] WEINER J, BAGNATO V S, ZILIO S, et al. Experiments and theory in cold and ultracold collisions [J]. Reviews of Modern Physics, 1999, 71(1): 1-85.

[6] VERHAAR B J. Collisions of ultracold atoms: theory and examples[J]. Laser Physics, 1994, 4(5): 1050-1061.

[7] SNIDER R F. Quantum-mechanical Modified equation for degenerate internal states[J].The Journal of Chemical Physics, 1960, 32(4): 1051-1060.

[8] KOELMAN J M V A, CRAMPION S B, STOOF H T C, et al. Spin-exchange frequency shifts in cryogenic and room-temperature hydrogen masers[J]. Physical Review A, 1988, 38(7): 3535-3547.

[9] TIESINGA E, VERHAAR B J, Stoof H T C, et al. Spin-exchange frequency shift in a cesium atomic fountain[J]. Phys. Rev. A, 1992, 45(5): R2671-R2673.

[10] GIBBLE K, CHU S. Laser-cooled Cs frequency standard and a measurement of the frequency shift due to ultracold collisions[J]. Physical Review Letters, 1993, 70(12):1771-1774.

[11] SORTAIS Y, BIZE S, NICOLAS C, et al. Cold collision frequency shifts in a 87Rb atomic fountain[J]. Physical Review Letters, 2000, 85(15): 3117-3120.

[12] LEVI F, CALONICO D, LORINI L, et al. IEN-CsF1 primary frequency standard at INRIM: accuracy evaluation and TAI calibrations[J]. Metrologia, 2006, 43(6): 545-555.

[13] SZYMANIEC K, PARK S E. Primary frequency standard NPL-CsF2: optimized operation near the collisional shift cancellation point[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(7): 2475-2481.

[14] PEREIRA DOS SANTOS F, MARION H, BIZE S, et al. Controlling the cold collision shift in high precision atomic interferometer[J]. Physical Review Letters, 2002, 89(23): 233004-1.

[15] GERGINOV V, NEMITZ N , WEYERS S, et al. Uncertainty evaluation of the cesium fountain clock PTB-CSF2[J]. Metrologia, 2010, 47(1): 65-79.

Research on differential measurement method of the cold atomic collision shift in the Cesium fountain clock

LIN Rui1, 2, 3, WANG Xin-liang1, 2, 3, LIU Dan-dan1, 2, 3, GUAN Yong1, 2, 3, ZHANG Hui1, 2, CHEN Jiang1,2,3, YU Feng-xiang1,2,3, SHI Jun-ru1,2, RUAN Jun1,2, ZHANG Shou-gang1,2,4

(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China; 2.Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China; 3.University of Chinese Academy of Sciences, Beijing 10049, China; 4. School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 100049, China)