影响脉冲星时稳定度的因素分析

丁勇恒，童明雷，赵成仕



影响脉冲星时稳定度的因素分析

丁勇恒1,2,3，童明雷1,2，赵成仕1,2

（1. 中国科学院 国家授时中心，西安 710600；2. 中国科学院 时间频率基准重点实验室，西安 710600；3. 中国科学院大学，北京 100049）

毫秒脉冲星自转的高度稳定性，使之成为一种理想的时间尺度，称为脉冲星时。但影响脉冲星时稳定度的因素仍有很多，例如观测白噪声、计时红噪声、参考原子钟钟差、太阳系历表误差、宇宙中的引力波等等。为建立高精度的脉冲星时，主要分析3种因素如何影响脉冲星时的稳定度，分别是参考钟钟差、太阳系历表误差以及随机背景引力波。利用TEMPO2软件，结合Parkers脉冲星计时阵（PPTA）的真实观测数据和模拟数据来具体分析各个不同因素对脉冲星时的影响。我们发现在对所有脉冲星计时模型参数拟合后，历表误差对脉冲星时稳定度的影响较小，而参考原子钟钟差和引力波对脉冲星长期稳定度影响比较大。

脉冲星时；太阳系行星历表；原子时；引力波

0 引言

脉冲星是高速自转的中子星，自转非常稳定，其中毫秒脉冲星的自转周期一般小于20 ms，周期随时间的变化率可达10-20。因此，毫秒脉冲星可以作为一种理想时钟。毫秒脉冲星脉冲到达时间（TOA）的测量是以原子时为参考，利用连续多年的TOA观测数据，采用最小二乘拟合可得到脉冲星的自转参数（自转频率和自转频率变化率）、天体测量参数（位置、自行和时差）、双星轨道参数（如果是脉冲星处于双星系统中）等计时模型参数。由观测到的TOA减去计时模型预报的TOA，便得到脉冲星计时残差[1]。脉冲星短期稳定度比原子时差，主要是受到计时观测误差的影响。但随着时间的累积，脉冲星时稳定度会优于原子时的稳定度。这是脉冲星时的一个优势，即长期稳定性好。影响脉冲星时的主要误差源有：① 测量误差（辐射计噪声、脉冲相位颤动误差），时间比对系统误差（小于10 ns）；② 脉冲星本身自转不稳定引起的计时红噪声 ；③ 星际介质色散的变化引起的红噪声；④ 地球历表误差和太阳系天体质量误差（约几十纳秒量级）；⑤ 引力波影响（约几十到100ns量级）；⑥ 计时模型和算法误差；⑦ 观测系统的噪声。

Hobbs等人[1]讨论了利用Parkes脉冲星计时阵（PPTA）的计时观测数据，利用全局拟合钟差的方法初步建立了综合脉冲星时间尺度，并检测到了国际原子时TAI相对于地球时TT的随机波动，这足以说明脉冲星时的高度稳定性。然而，该文并没有直接计算脉冲星时的长期稳定度。Rodin基于维纳滤波的方法，利用两颗毫秒脉冲星建立了综合脉冲星时间尺度，并且计算了脉冲星时的长期稳定度[2]。本文主要讨论原子时误差、太阳系行星历表误差和引力波背景如何影响单颗脉冲星时的稳定度，暂不讨论综合脉冲星时的情况。

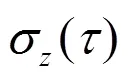
1 脉冲星计时模型

脉冲星发射的信号在到达地球的过程中，在经过星际间气体与等离子体时发生散射与色散，星际间物质导致接收到的信号与原信号相比发生形变，且不同波长的电磁波在介质中传播速度不同，它们到达地球的时间也就不同，因此需要经过色散改正。此外还需要进行Roemer延迟、Einstein延迟、Shapiro延迟和双星轨道延迟改正[4-6]：

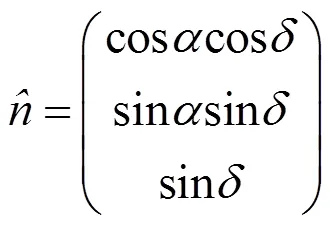
脉冲星靠消耗自转能而弥补辐射出去的能量，因而自转会逐渐变慢，故其自转频率变化率不为0。脉冲星自转模型表示为[7]：

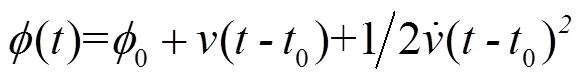
2 脉冲星时稳定度的估计方法

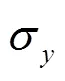
3 太阳系行星历表误差的影响

从20世纪60年代，美国喷气推进实验室（JPL），发布了多份太阳系行星历表（DE/LE系列[9]），最新的DE432建于2014年。为比较不同历表的影响，我们采用3种不同历表，分别是DE200, DE405和DE421。

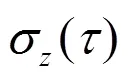
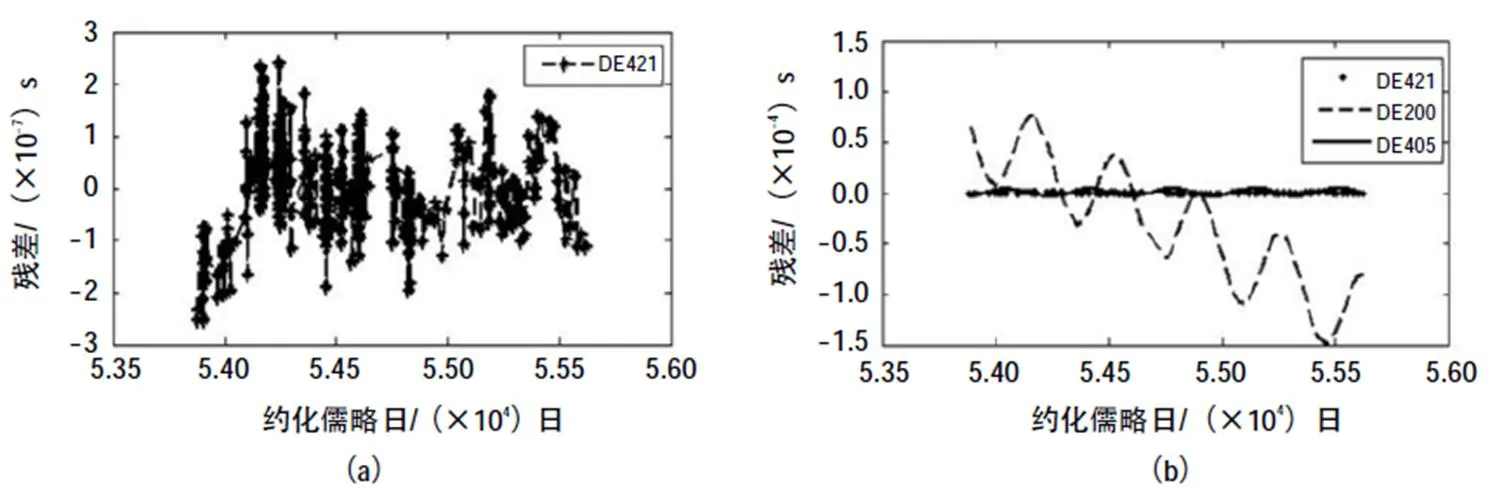
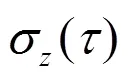
4 原子时钟差的影响

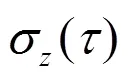
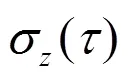
图3 不同参考原子钟的脉冲星时稳定度

5 引力波背景的影响

原子钟钟差对观测的所有脉冲星计时残差影响相同，呈单极性；对于位于空间相同方向的两颗脉冲星，地球历表误差对其计时残差影响符号相同，对位于空间相反方向的两颗脉冲星，地球历表误差对其计时残差影响符号相反，大小则与脉冲星的黄纬有关，呈偶极性；引力波对相对于测站张角为0o或180o分布的两颗脉冲星的计时残差影响符号相同，而对张角为90o的两颗脉冲星的计时残差影响符号相反，呈四极性。引力波有多种形式，不同形式的引力波对脉冲星计时残差的影响文献[11]中已讨论的比较详细。下面我们只分析随机引力波背景对脉冲星时稳定度的影响。

随机引力波背景的成因主要分为3种：宇宙中多个双星系统的绕转和并合形成的随机背景、宇宙暴涨后期形成的残余引力波背景以及宇宙弦模型预言的引力波背景。这3种背景引力波的幅度特征谱在脉冲星计时阵的响应频率范围内，都可以简单地表示为幂率形式：

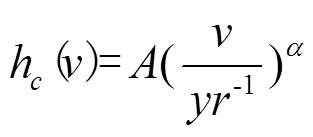
式（7）中，为引力波的幅度，为引力波的频率，为谱指数。本文总是假设引力波背景的特征谱具有式（7）的形式，根据目前的观测，只能给出A的上限。为了清楚地看到引力波对脉冲星时稳定度的影响，用Tempo2软件分别模拟了不同幅度和谱指数的引力波背景，即模拟数据中包含背景引力波信号和观测白噪声，其中背景引力波的谱具有式（7）的形式，而每次模拟A和的值可以改变。图4表示了不同引力波背景幅度对脉冲星时稳定度的影响，其中均取为-2/3，表示的是多个双星系统的绕转和并合形成的随机背景。三角形虚线为无引力波的情况，圆圈虚线表示引力波幅度为10-15的情况，而雪花虚线代表引力波幅度为10-14的情况。可以清楚地看到，在短时标内，引力波对脉冲星稳定度几乎无影响，但在长时标上引力波幅度越大脉冲星时稳定度越差，也就意味着引力波影响越明显。

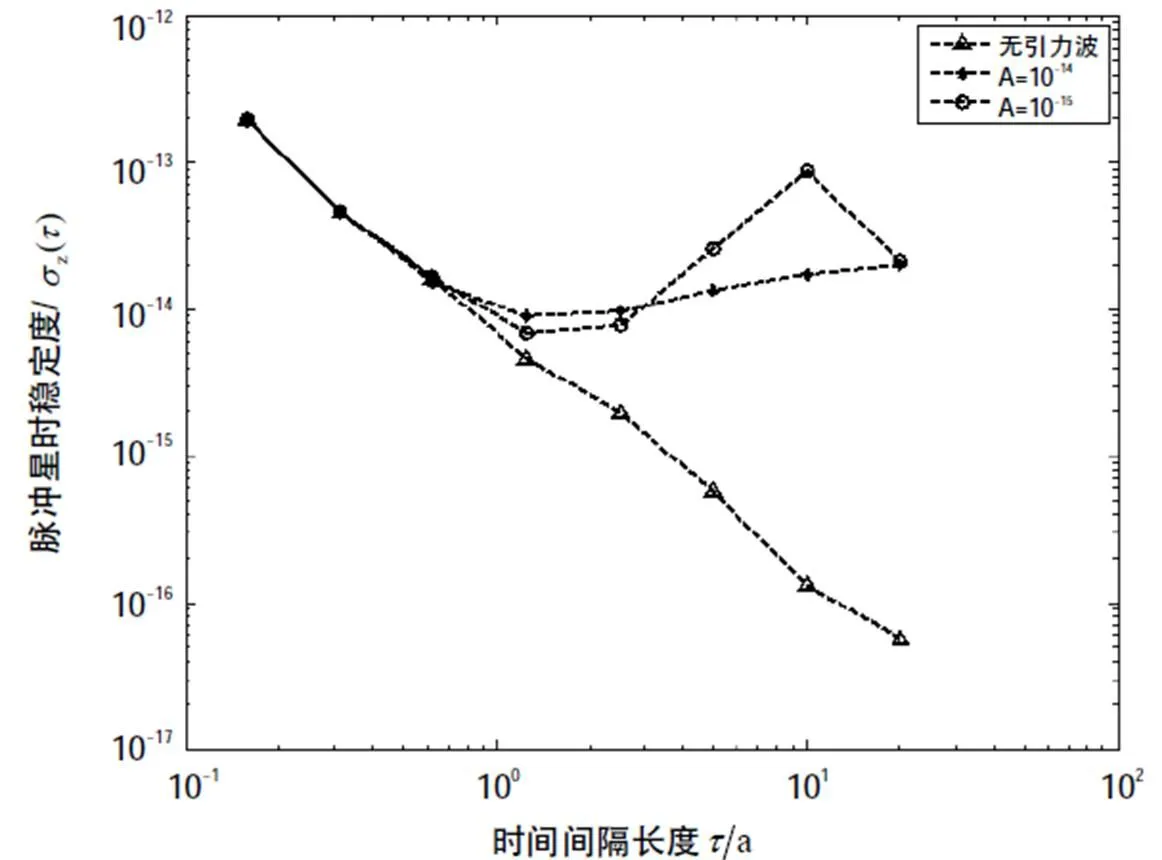
图5 不同谱指数引力波背景对脉冲星时稳定度的影响

6 结语

本文分析了太阳系行星历表误差，参考原子时误差和引力波这3种因素对脉冲星时稳定度的影响。首先，为检验历表误差对脉冲星时的影响，我们选取了DE200，DE405和DE421 3个不同版本的太阳系行星历表，比较了其中的差别。尽管不同DE历表得到的拟合前计时残差差别较大，但如果将自转参数和天体测量参数都作拟合，则拟合后计时残差差别不大，从而对脉冲星时稳定度影响也不明显。这与Hobbs在文献[1]中给出的结论一致。因此，若历表有误差，在做脉冲星参数拟合时，不能只拟合自转参数，天体测量参数也要拟合。其次，为分析原子钟误差对脉冲星时影响，我们选取了美国国家标准与技术研究院和中国科学院国家授时中心保持的地方原子时作为脉冲星TOA的参考钟，并将之与以TT为参考的情况作比较。我们发现，以地方原子时为参考钟比以TT为参考钟的脉冲时稳定度差很多。这说明地方原子时的不稳定性被吸收到脉冲星时中。另一方面也说明了脉冲星计时观测的测站钟钟差改正的重要性，而用TT作为参考钟来进行脉冲星计时是最可靠的。最后，我们讨论随机引力波背景对脉冲星时的影响。由于至今没有在脉冲星探测引力波的频段上直接探测到引力波，因而我们利用了模拟数据。我们分析了背景引力波的不同幅度和不同谱指数两种情况，发现引力波在脉冲星长时标上的稳定度影响很明显。一方面，对于同一谱指数引力波幅度越大，其对脉冲星时稳定度影响越大；另一方面，对于同一幅度的引力波，谱指数为-1的引力波背景比谱指数为-2/3的引力波背景对脉冲星时的稳定度影响更大。因此引力波是建立高精度脉冲星时的一个潜在的干扰因素，应该想办法根据引力波的理论模型予以消除。这也是今后我们要研究的一个课题。对于这几种因素如何影响综合脉冲星时的稳定度，我们将在后续的工作中讨论。

[1] HOBBS G, COLES W, MANCHESTER R, et al. Development of a pulsar-based time-scale[J]. Monthly Notices of the Royal Astronomical Society, 2012, 427(4): 2780-2787.

[2] RODIN A E. Optimal filters for the construction of the ensemble pulsar time[J]. Monthly Notices of the Royal Astronomical Society, 2008, 387(4): 1583-1588.

[3] MATSAKIS K N, TAYLOR J H, EUBANKS T M, et al. A statistic for describing pulsar and clock stabilities[J]. Astronomy &Astrophysics, 1997, 326(326): 924-928.

[4] HOBBS G B, EDWARDS R T, MANCHESTER R N. TEMPO2: a new pulsar-timing package-I. An overview[J]. MNRAS, 2010, 369(2): 655-672.

[5] EDWARDS R T, HOBBS G B, MANCHESTER R N, TEMPO2: a new pulsar-timing package-II. The timing model and precision estimates[J]. Monthly Notices of the Royal Astronomical Society, 2006, 372(4): 1549-1574.

[6] HOBBS G, JENET F, LEE K J, et al. TEMPO2: a new pulsar timing package-III. Gravitational wave simulation[J]. Monthly Notices of the Royal Astronomical Society, 2009, 394(4): 1945-1955.

[7] LORIMER D R. Binary and Millisecond Pulsars[J/OL]. Living Reviews in. Relativity, 2008, 11: 08. [2016-12-11].http://www.livingreviews.org/lrr-2008-8.

[8] 仲崇霞, 杨廷高. 脉冲星时间稳定度的估计方法[J]. 时间频率学报, 2004, 27(1): 129-137.

[9] 邓雪梅, 樊敏, 谢懿. JPL行星历表的比较及评估[J]. 天文学报, 2013, 54(6): 550-561.

[10] MANCHESTER D, HOBBS G, BAILE M, et al. The Parkes Pulsar Timing Array Data Release 1[DB/OL]. (2010-09-08)[2016-12-11]. http://dx.doi.org/10.4225/08/534CC21379C12.

[11] 童明雷, 丁勇恒, 赵成仕, 等. 引力波引起的脉冲星计时残差模拟与分析[J]. 时间频率学报, 2015, 38(1): 44-51.

Analyses of factors affecting the stability of pulsar time scale

DING Yong-heng1,2,3, TONG Ming-lei1,2, ZHAO Cheng-shi1,2

(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. Key Laboratory of Time and Frequency Primary Standards, National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100049, China)

Millisecond pulsars have high rotating stability, which makes them as an ideal time scale, so-called pulsar time. However, there are still many factors affecting the stability of pulsar time, such as the observational white noise, the timing red noise, the atomic clock error, the solar system ephemeris error, the cosmic gravitational waves and so on. In order to establish high-precision pulsar time, three factors affecting the stability of pulsar time were analyzed in this paper, they are atomic clock error, solar system ephemeris error and gravitational wave background respectively. The software TEMPO2 was used to analyze the effects of various factors on the pulsar time based on the real data observed by Parkers pulsar timing array (PPTA) and the simulated data. After all the pulsar timing model parameters were fitted, the results showed that the effect of the solar system ephemeris error on the stability of pulsar time scale is small, however, the reference atomic clock error and the cosmic gravitational waves contribute significant impacts on the long-term stability of pulsar time scale.

pulsar time; solar system ephemeris error; atomic time scale; gravitational wave

P127.1

A

1674-0637（2017）04-0260-08

10.13875/j.issn.1674-0637.2017-04-0260-08

2017-04-22

国家自然科学基金资助项目（U1531112，11403030）；中国科学院“西部之光”西部青年学者A类资助项目（XAB2015A06）；陕西省青年科技新星资助项目（2015KJXX-56）；中国科学院青年创新促进会资助项目（2017450）

丁勇恒，男，硕士，主要从事脉冲星计时应用研究。