基于转发式分时观测的IGSO卫星定轨研究
2017-02-05陈琪雷辉杨旭海陈亮王伟
陈琪,雷辉,杨旭海,陈亮,王伟
基于转发式分时观测的IGSO卫星定轨研究
陈琪1,2,3,雷辉1,2,杨旭海1,2,3,陈亮1,2,王伟1,2
(1. 中国科学院 国家授时中心,西安 710600; 2. 中国科学院 精密导航定位与定时技术重点实验室,西安 710600; 3. 中国科学院大学 天文与空间科学学院,北京 100049)
卫星轨道精度是决定卫星导航系统性能的关键因素之一。在转发式卫星导航的试验项目的支持下,对I1-S卫星的观测数据进行分时段处理,模拟分时观测的过程,利用处理后的数据进行定轨。目的是验证在数据量少的情况下是否不影响定轨精度,如果结论成立,则可以在有多个观测任务时,对不同的卫星进行轮替观测,提高设备的利用率。利用2015年8月14日到2015年8月20日的观测资料进行定轨实验,分别从定轨残差以及轨道重叠误差等方面分析卫星的定轨精度,5站总的RMS在0.14~0.17m的范围之内,平均值是0.15m。在三维方向上的重叠差小于1 m。利用分时观测的数据进行定轨,5站总的残差RMS都小于0.20 m,在0.13~0.18 m的范围内,分时段数据解算的卫星轨道与全时段解算的轨道比较差异RMS小于1 m,和全时段定轨残差在同一水平上,没有降低定轨精度,证明了在米级定轨需求下分时观测的可行性。
卫星定轨;分时观测;转发式测定轨技术;轨道重叠误差
0 引言
卫星轨道的误差直接影响卫星导航系统用户的定位精度,因此,精确地确定卫星轨道是卫星导航定位的保障[1]。测定卫星轨道的方法各不相同。GPS全球定位系统用伪距法测轨,它在全球布站,数据统一解算,其广播星历表给出的卫星位置精度约为2.60 m,GPSⅢ将会提高到1.50 m。GLONASS全球卫星导航系统把测轨和时间同步分开,轨道借助于雷达测距,测距精度为2~3 m,每颗GLONASS卫星装有激光反射器,用激光测距对雷达观测结果进行校验。GLONASS最终的定轨精度和GPS相当[2]。转发式卫星导航试验系统将导航频率基准和时间基准的原子钟直接安置在地面导航中心站上,利用卫星转发器转发上行导航信号后广播下行的方式实现导航定位。地面原子钟精度高稳定性好,易于保养、管理、更换和维修,还可以根据原子钟技术的进步及时更换新设备提高精度,做到与时俱进。这样做不但解决了星载原子钟研制的技术瓶颈,而且减轻空间导航卫星研制的压力,大大减少空间投资[3]。
本文在转发式卫星测轨和定轨的试验项目支持下,对I1-S卫星进行观测,对原始数据进行分时段处理,通过此方法来模拟分时观测模式,再进行轨道确定。通过观测资料的拟合程度和重叠弧段误差两种方法分析结果,来验证对数据分时段处理的定轨实验是否可行,在数据量少的情况下能否不影响定轨精度。如果结论成立,那么可以在观测时对不同的卫星进行轮替观测,提高设备的利用率。
1 基础条件
转发式卫星测轨方法的原理是用各卫星地面站的原子钟产生的高精度时间信号,用不同伪码调制,同时向同一颗卫星发射相同载频的伪码扩频信号,经卫星转发器转向各卫星地面站,每个地面站接收到所有台站发送的时间信号,测定信号路径的时延[4-8]。各台站仅接收卫星转发自己台站发射的信号,这种观测形成了转发式自发自收测轨模式;各台站接收同一台站发射的信号,这种组合形成了转发式一发多收观测模式;用多站发多站接收各站信号,这种组合形成转发式多发多收对观测模式;主站收副站信号,副站收主站信号,这种组合形成转发式主从对观测模式[9]。
实验的观测模式是选择轨道倾角为55°的北斗IGSO试验卫星I1-S卫星进行自发自收观测。该卫星过赤道上空时的星下点经度为东经95°。
本文利用2015年8月14日到2015年8月20日的观测资料进行定轨实验。利用5个站(分别位于长春、西安、昆明等地)的C波段转发式数据进行定轨。图1给出了这一批数据的分站观测数据情况。横坐标表示的是年积日,纵坐标是时延值。

图1 2015-08-14/2015-08-20的北斗IGSO卫星观测数据图
2 全时段定轨结果分析
在上述观测条件下,对于得到的观测数据,采用的定轨策略为:定轨弧长3d,滑动窗口选取1d,解算卫星位置、速度、太阳光压系数、方向经验加速度系数及各测站系统差。
从定轨残差和重叠弧段误差两个方面对定轨结果进行分析。
2.1 观测资料的拟合程度
观测资料的拟合程度也就是残差RMS,是衡量轨道精度的一个重要的指标,能在一定程度上反映实际定轨精度。表1给出了北斗I1-S卫星5个站的定轨残差。图2给出了2015年8月17日至2015年8月20日3d定轨的残差分布图(其中最后一次定轨用的弧长为2 d)。
表1 北斗IGSO卫星各站定轨残差的RMS值 m
从图2中得出,残差大致都在-0.40~0.50 m的范围内。由表1中可知5站总的残差RMS在0.14~0.17 m的范围之内,平均值为0.15m。
2.2 重叠弧段误差
在计算时,使得相邻计算弧段有一段较短时间的重叠,然后从这段时间内两相邻弧段卫星轨道的符合程度来判断轨道的精度。通常定轨中弧段的中间部分认为结果最好,可以作为标准轨道与下一次定轨的轨道进行比较。
通常以重叠弧段轨道差异的三维的RMS作为衡量指标,具体计算公式为
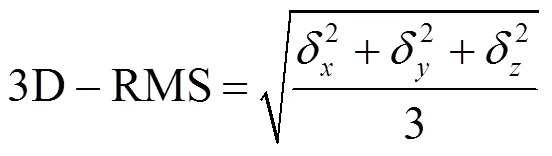
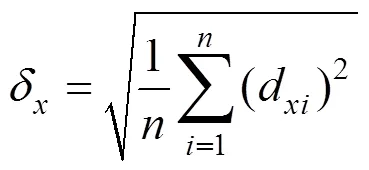
在本文的定轨实验中,定轨弧段为3 d,每两次相邻定轨有2 d重叠。取第1次计算弧段的中间1 d与下一弧段的第1天轨道比较。示意图如下,阴影部分表示被比较的1 d轨道。共进行了6次定轨,有5个重叠弧段。结果分析如表2所示。

图3 重叠轨道的选取示意图
表2 北斗IGSO卫星重叠弧段轨道差RMS值

从表2中可以看轨道重叠误差在方向比较小,都小于0.1m。由于2015年8月18号的重叠差在,,三维位置方向都有跳动,使轨道重叠误差平均值偏大。方向的平均水平是0.07m,方向的平均水平在0.55 m,方向的平均水平在0.62 m左右,在三维位置上为0.85 m。剔除8月18日的轨道差的结果,得出的方向的平均水平是0.07m,方向的平均水平在0.48 m,方向的平均水平在0.40 m左右,在三维位置上为0.63m。
图4给出了2015年8月14日至2015年8月20日的重叠轨道差。由图3可以看出,IGSO卫星各个重叠弧段的径向轨道误差小于0.20 m,三维位置差绝大部分小于1 m。
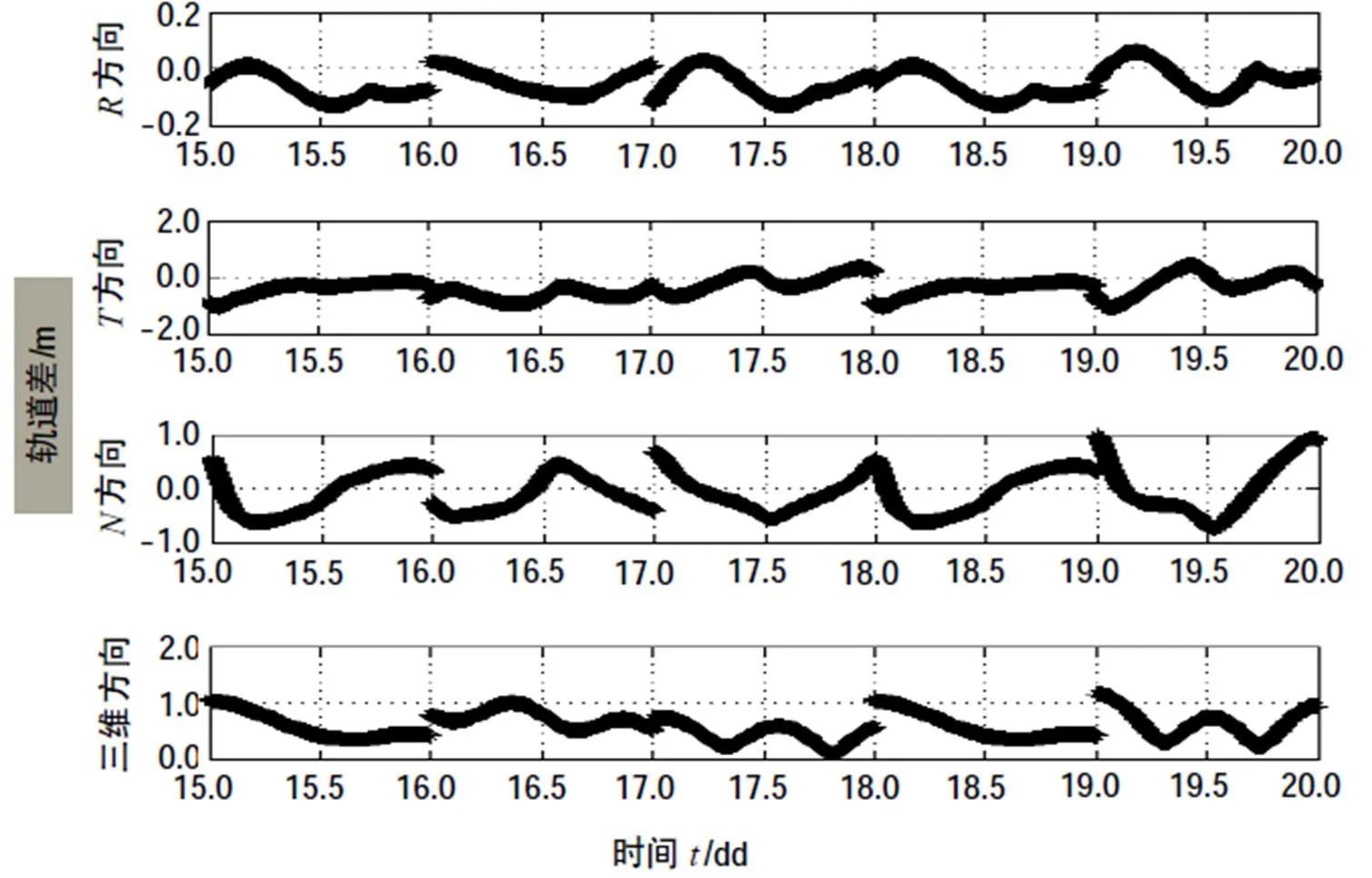
图4 北斗IGSO卫星重叠弧段轨道差
3 分时段定轨结果分析
为了可以对不同的卫星进行轮替观测,提高各设备的利用率。对原始数据进行分时段处理,进行试验分析。原始数据是10 s采集一个数据,本文对分时段处理拟采用的方法有以下3种:
①二分之一数据:将数据按30min间隔划分,将每小时数据的后半小时数据剔除,保留剩下的二分之一数据进行定轨。如图5所示,一段表示30min的数据,剔除数据后只需要下图黑色区域的数据。即保留0~30 min的数据,剔除30~60 min的数据,保留60~90 min的数据,剔除90~120 min的数据。

图5 二分之一数据分时处理示意图
②三分之一数据:将数据按30min间隔划分,在每3段数据中,保留第1段30min的数据,剔除后两段30min的数据。例如,保留第1段0~30min的数据,剔除30~60min,60~90min的数据。图6为三分之一数据分时处理示意图。

图6 三分之一数据分时处理示意图
③四分之一数据:与上述方法类似,将数据按30min间隔划分,保留第1段30min的数据,剔除后3段30 min数据。图7为四分之一数据分时处理示意图。

图7 四分之一数据分时处理示意图
3.1 二分之一数据定轨分析
将2015年8月14日至2015年8月20日的这一批数据分时段处理之后,分别对二分之一的数据,三分之一的数据,四分之一的数据进行定轨试验。按照第2节介绍的定轨分析方法,对分时策略的定轨结果进行分析,并且将解算出的轨道与基于全时段数据解算出的轨道相比较,分析轨道差异。以及下面首先分析二分之一数据的定轨情况,图8为二分之一数据8月17日到8月20日3 d定轨的残差图。分别对5个站的残差结果进行作图分析,并将数据结果统计在表3中。
从图8中可以看出,残差的范围与全部数据计算的定轨残差的范围相比没有变化。只是数据量减少了大约一半。从表3可以看出5站总的残差RMS在0.14~0.17 m的范围内,平均值是0.16 m。精度和全部数据定轨结果相当。

图8 二分之一数据2015-08-17/2015-08-20 3d弧段的北斗IGSO卫星定轨残差
表3 2015-08-14/2015-08-20二分之一数据北斗IGSO卫星各站定轨残差RMS m

表4表示的是利用二分之一数据解算出的3 d轨道与利用全部数据解算出的3 d轨道比较结果。即利用二分之一数据解算的3 d轨道与基于全时段数据解算的3 d轨道比较。
表4 利用二分之一数据解算的轨道与利用全部数据解算的轨道比较
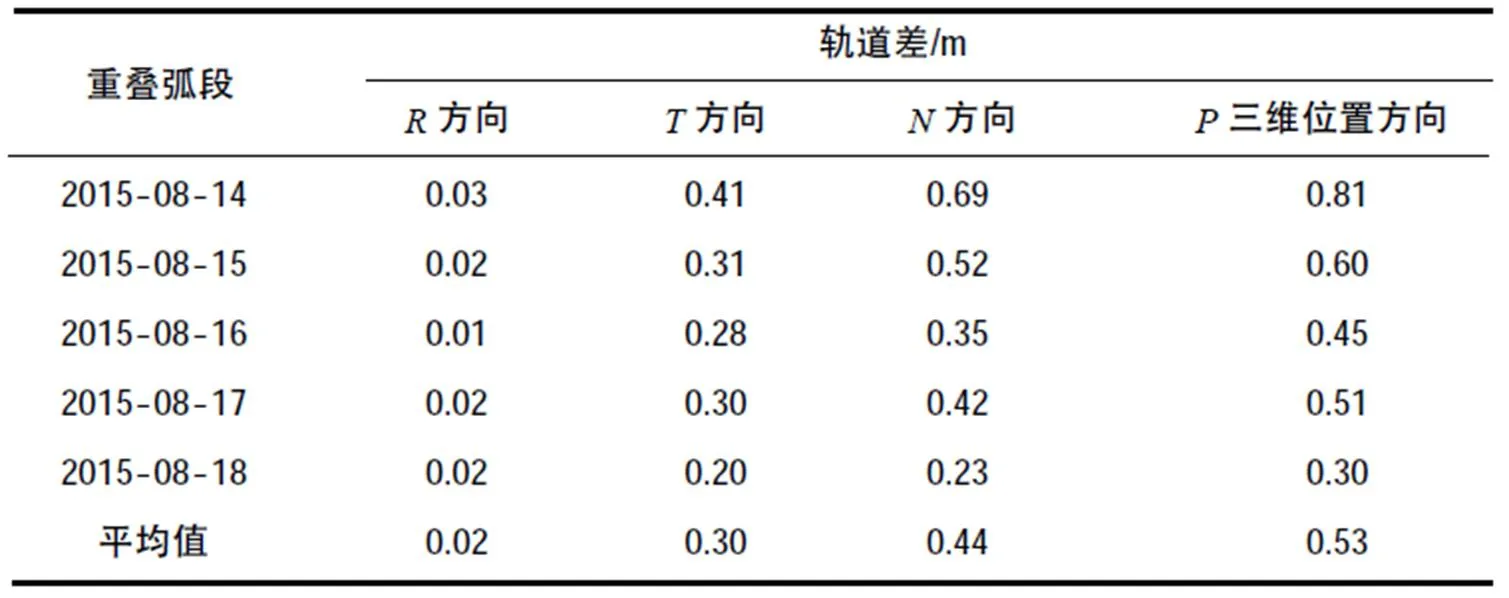
从表4中可以看出,对每一次解算出的3 d的轨道,它们之间比较的结果为,在方向平均值0.02 m,在方向平均值为0.30 m,在方向平均值为0.44 m,在三维位置方向为0.53 m。可以看出轨道的重叠误差整体较小,利用二分之一解算出的轨道与全部数据解算出的轨道偏差不大。
3.2 三分之一数据定轨分析
分析三分之一的数据定轨结果,图9表示利用三分之一数据量进行2015年8月17日至2015年8月19日3d弧段定轨的残差图。并且将残差按观测站来划分。并将残差结果记录表5中。

图9 三分之一数据的2015-08-17/2015-08-20 3d弧段的北斗IGSO卫星定轨残差
表5 2015-08-14/2015-08-20三分之一数据北斗IGSO卫星各站定轨残差RMS m

从图9中可以看出,残差的范围与全部数据计算的定轨残差的范围相比没有变化。只是残差的数据量减少到三分之一。从表5可以看出5站总的残差RMS范围并没有太大变化,大约在0.14~0.17m的范围内,总残差RMS平均值为0.15 m。
表6表示的是利用三分之一数据解算出的3 d轨道与利用全部数据解算出的3 d轨道比较结果。
表6 利用三分之一数据解算轨道与利用全部数据解算的轨道比较
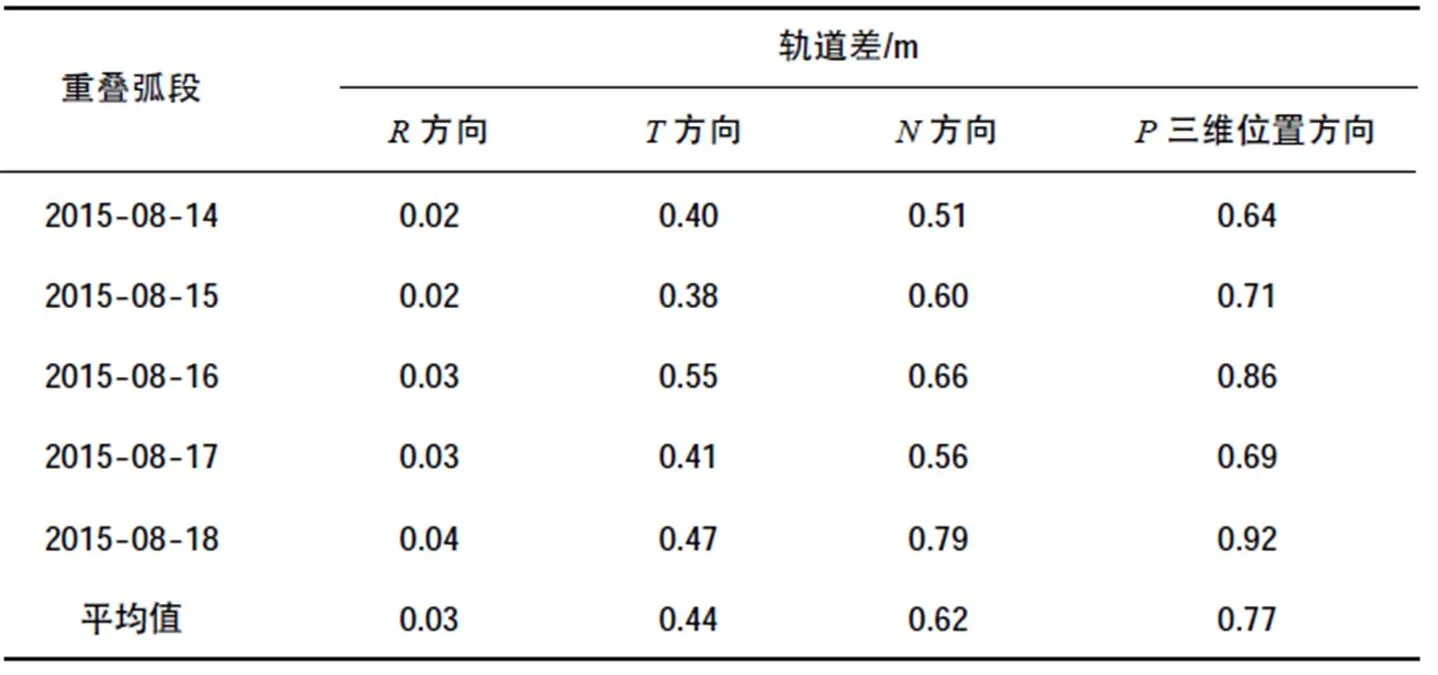
从表6中可以看出,对每一次解算出的3 d的轨道,它们之间比较的结果为:在方向平均值0.03 m,在方向平均值为0.44 m,在方向平均值为0.62 m,在三维位置方向为0.77 m。结果与表4结果相比,误差相对增大,但是总体还是小于1 m。
3.3 四分之一数据定轨分析
分析四分之一的定轨结果,图10给出了四分之一数据8月17日到8月20日3 d定轨的残差图。从图中可以看出,残差的范围与全部数据计算的定轨残差的范围相比没有太大的变化。残差的数据量相比完整数据来说大约减少了四分之一。从表7可以看出,利用四分之一数据进行定轨残差RMS值和利用全部数据进行定轨的残差RMS值大小变化不大。总残差RMS平均值为0.15 m。

图10 四分之一数据2015-08-17/2015-08-20 3d弧段的北斗IGSO卫星定轨残差
表7 2015-08-14/2015-08-20四分之一数据北斗IGSO卫星各站定轨残差RMS m

表8表示的是利用四分之一数据解算出的3 d轨道与利用全部数据解算出的3 d轨道比较结果。
表8 利用四分之一数据解算的轨道与利用全部数据解算的轨道比较
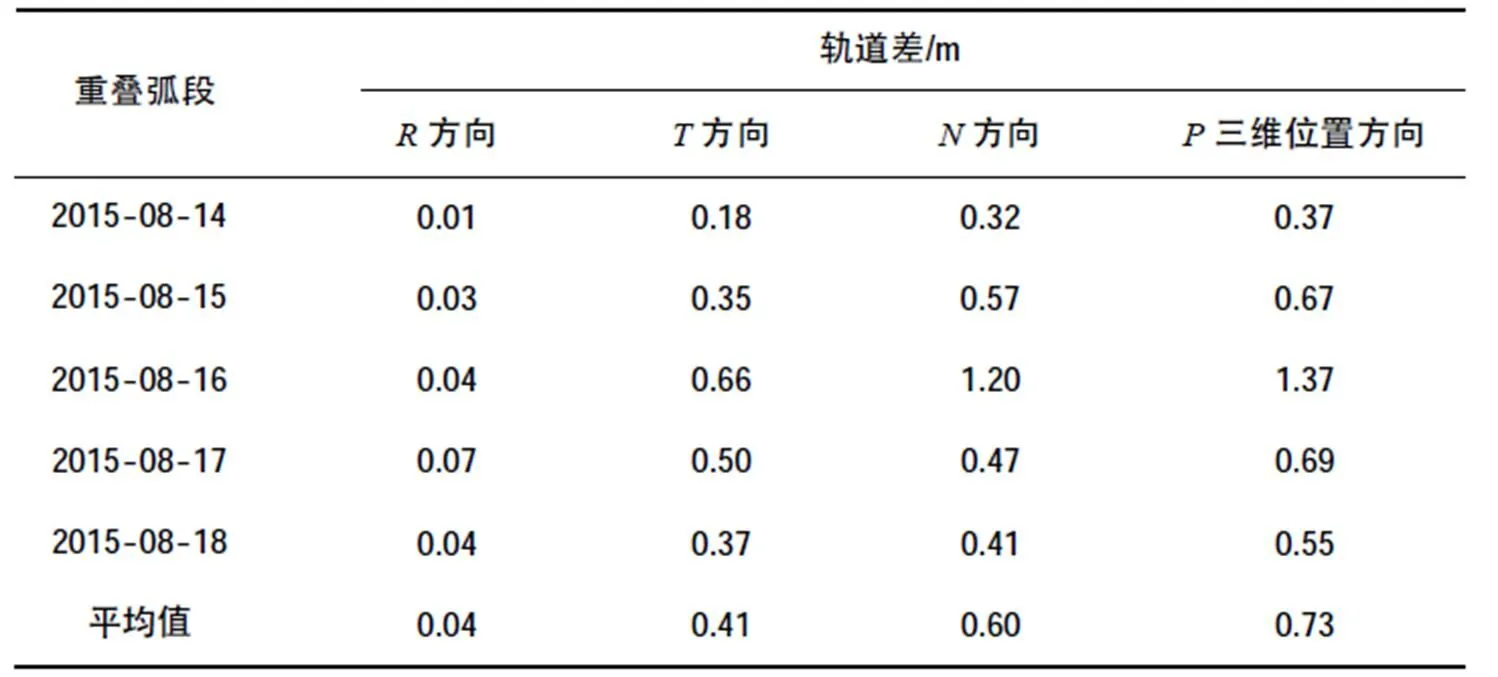
从表8中可以看出,对每一次解算出的3 d的轨道,它们之间比较的结果为:在方向平均值0.04 m,在方向平均值为0.41m,在方向平均值为0.60m,在三维位置方向为0.73m。对于2015年8月16号这一天为起始时间计算的3 d轨道,与全部数据计算的轨道结果在方向和方向都大于1m。但总体结果还是小于1 m,证明利用四分之一数据计算出轨道与全部数据计算出的轨道偏差不大。
4 结语
笔者从对I1-S观测的2015年8月14日到2015年8月20日数据,将数据进行分时段处理,再进行定轨解算,通过观测资料的拟合度和重叠弧段方法分析定轨的精度,利用全时段进行定轨,5站总的残差RMS在0.14~0.17 m的范围之内,平均值是0.15 m。轨道重叠误差方向的平均水平是0.07m,方向的平均水平在0.55 m,方向的平均水平在0.60 m左右,在三维位置上为0.98 m。利用分时观测的数据进行定轨,5站总的残差RMS都小于0.20 m,在0.13~0.18 m的范围内。并且将基于不同分时策略的定轨结果与基于全时段数据的定轨结果进行比较分析,得出的轨道重叠误差均小于1 m。通过分析结果,分时段数据解算的残差RMS值,以及与全时段解算的轨道比较的RMS值,和全时段定轨误差在同一水平上,没有降低定轨精度,所以在米级定轨精度的标准上,在观测数据量较少的情况下,或者需要对不同卫星进行轮替观测时,分时观测是在不影响定轨精度并且提高设备利用率的一种可行性方法。还可以利用不同方法进行分时段处理,利用更多数据进行分析。计划在以后的工作中进一步完善。
[1] 杜兰. GEO卫星精密定轨技术研究[D]. 郑州: 解放军信息工程大学, 2006.
[2] 宋小勇. COMPASS导航卫星定轨研究[D]. 西安: 长安大学, 2009.
[3] 李志刚, 杨旭海, 施浒立, 等. 转发器式卫星轨道测定新方法[J]. 中国科学G辑, 物理学 力学 天文学, 38(12): 1711-1722.
[4] 黄珹, 冯初刚. SLR数据处理及其软件实现[G]. 上海: 中国科学院上海天文台, 2003.
[5] 李济生. 人造卫星精密轨道确定[M]. 北京: 解放军出版社, 1995.
[6] 雷辉, 李志刚, 杨旭海, 等. 基于转发式的北斗卫星导航系统地球静止轨道卫星精密定轨试验[J]. 测绘学报, 2011, 40(S): 31-33.
[7] 杨旭海, 丁硕, 雷辉, 等. 转发式测定轨技术及其研究进展[J]. 时间频率学报, 2016, 39(3): 216-224.
[8] 施浒立, 孙希延, 李志刚. 转发式卫星导航原理[M]. 北京: 科学出版社, 2009.
[9] 雷辉. 基于转发式的导航卫星精密定轨研究[D]. 西安: 中国科学院国家授时中心, 2011.
Research of BDS-IGSO satellite orbit determination based on ODTT time-sharing observation
CHEN Qi1,2,3, LEI Hui1,2, YANG Xu-hai1,2,3, CHEN Liang1,2, WANG Wei1,2
(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China; 2. Key Laboratory of Precise Positioning and Timing Technology, National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China; 3. School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 100049, China)
The satellite orbit accuracy is one of the key factors that affect the performance of the navigation satellite system. Since the orbit determination accuracy is greatly influenced by the measurement conditions, the observation data of I1-S satellite time-sharing processing on the basis of orbit determination by transfer tracking(ODTT)and processed data are used for orbit determination in this paper. One of the purposes is to verify whether the small amount of data will not affect the precision of orbit determination, the other is to improve the utilization rate of equipment by observing different satellites in turn. In this paper, the observation data from August 14, 2015 to August 19, 2015 is used for orbit determination. The satellite orbit determination precision is analyzed by using the orbit residual error and orbital overlap error analysis respectively, the results show that the residual RMS of five stations is within 0.14 m to 0.17 m. The RMS of overlap differences in three-dimensional direction is less than 1m. By using the time-sharing observation data for orbit determination, the overall residual RMS values are less than 0.2 m, they are in the range of 0.13 m to 0.18 m. Thus, the feasibility of time-sharing observation under the requirement of meter-level orbit determination is proved.
satellite orbit determination; time-sharing observation; ODTT; orbital overlap error
P228
A
1674-0637(2017)04-0240-11
10.13875/j.issn.1674-0637.2017-04-0240-11
2017-04-16
国家自然科学基金面上资助项目(11173026)
陈琪,女,硕士研究生,主要从事卫星轨道研究。
