水下锥膛炮内弹道方程组的推导与计算

张 涛，侯 健，魏 平

(海军工程大学 兵器工程系，湖北 武汉 430033)

随着枪炮武器的大量研制、武器不断多元化，经典内弹道的基本方程组不能满足当前新型枪炮的内弹道状况。鉴于此，很有必要推导并完善经典内弹道理论，更真实地反映内弹道状况。有关火炮内弹道基本方程组推导和计算的研究有很多，其中孔德仁等[1]分析出水下枪械内弹道和经典内弹道的不同，指出：水下枪械枪管长度不宜太长，超过一定值后，初速反而下降且压力明显增大。梁志峰等[2]推导了空气炮内弹道基本方程组，与传统枪炮内弹道不同，空气炮是以空气为动力，压力变化规律是经典内弹道第2时期的变化情况。侯健等[3]根据压力与位移的关系，运用有限元软件得到锥膛炮内弹道数据，再通过引入次要功计算系数来优化内弹道曲线，这种方法可粗略推导出锥膛炮的内弹道模型，但此方法没有涉及到锥膛时期挤压阻力的推导。郭锦炎等[4]考虑弹体和壳体间有气体流失，较详细地推导出内弹道模型。李淼等[5]求解出弹带挤进有限元过程，将有限元计算的弹带应变能和摩擦消耗的能量引入到传统的内弹道能量方程，并考虑有锥度药室的火药气体压力分布。

针对因火炮工作环境、装置机构不同而导致经典内弹道基本方程组不适用或求解不精确的问题，上述学者在经典内弹道基础上，推导或优化了内弹道方程组。国内关于锥膛炮内弹道研究较少，笔者在锥膛炮空气中发射的基础上，研究锥膛炮在浸水模式下的内弹道基本方程组，考虑射弹弹裙在锥膛段挤压变形受到的阻力、弹前的变质量水柱和弹后空间压力变化3方面的影响，将三者耦合到内弹道计算中，最终推导出的水下锥膛炮内弹道方程组是一个分段微分方程组，并得出一些重要结论，此研究可为锥膛炮内弹道设计和弹炮匹配设计提供一定参考。

1 挤压阻力模型

射弹和锥膛炮结构如图1所示，射弹分为弹头、杆部和前、后弹裙三部分，锥膛炮分为第1直膛段、锥膛段和第2直膛段。射弹在锥膛炮内发射，弹裙在火药气体压力作用下，沿着第1直膛段运动，此阶段与传统内弹道方程相同[6]。当前弹裙运动至锥膛断面A-A处，在火药气体压力作用下，弹裙开始挤压塑性变形，由塑性变形引起的阻力逐渐增大。随着前弹裙挤压变形完成进入第2直膛段(断面B-B)时，挤压阻力开始减小，当后弹裙也挤压完成后挤压阻力消失，这时射弹完全进入第2直膛段，只受到摩擦力的作用。因此锥膛炮内弹道分为3段：第1直膛段、锥膛段和第2直膛段。

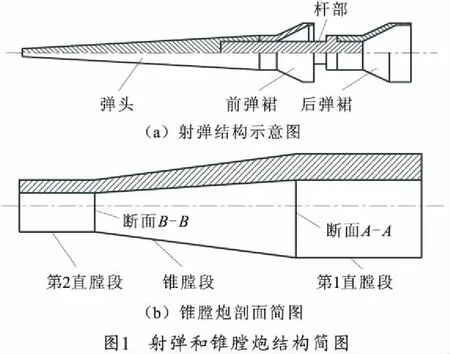
1.1 挤压过程

锥膛段的射弹运动十分复杂，为了便于分析，作如下假设：

1)挤压过程中，弹裙变形均匀。

2)前后弹裙变形伸长量均匀呈线性变化。

3)忽略火炮身管的弹塑性变形。

采用文献[6]提出的挤压阻力模型，并在其基础上考虑弹裙变形伸长量，现以前弹裙为例分析挤压阻力，后弹裙可以类似推导。如图2所示，弹裙通过锥膛段分为3段：第1段，前弹裙挤入锥膛，即图2(a)中梯形ABCD运动到A′B′C′D′，射弹在火药气体作用下向前运动，前弹裙开始塑性变形，图中阴影为挤压部分，伸长量为弹裙未变形前的长度与变形后的长度之差，即Δl=lq+lB′P-lm，母线长为lm的圆台表面积则是挤压接触面积；第2段，前弹裙全部挤进至前弹裙准备挤出锥膛，即图2(b)中梯形ABD′D运动到A′B′C′C，前弹裙处于逐渐成型过渡阶段；第3段，前弹裙准备挤出至全部挤出，即图2(c)中梯形ABCD运动到A′B′C′D′，至此，前弹裙挤压成型。

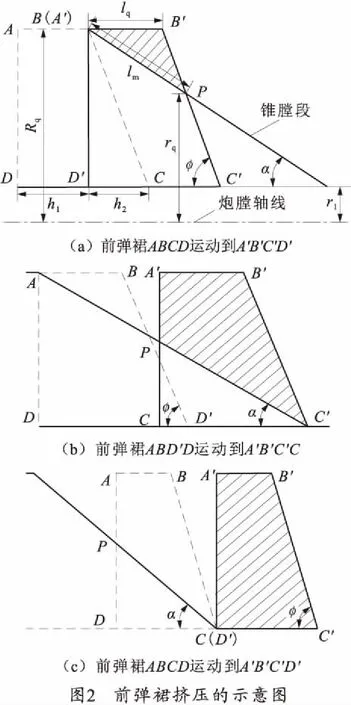
1.2 锥膛段阻力推导

对前弹裙受力分析可知，前弹裙受到的挤压阻力为摩擦力和正压力的合力，即：

Fq=σSi(sinα+μcosα)

(1)

式中：σ为材料的流动应力；μ为摩擦系数；α为锥膛半锥角；Si为挤压接触面，i=a,b,c。

根据图2所示前弹裙挤压的3个阶段，由几何关系可推出挤压接触面积Si为

(2)

(3)

Si=π(Rq+rq)(lm+Δl)

(4)

式中：Δl为变形伸长量；lq为前弹裙位移；Rq、rq分别为前弹裙挤压过程中前后半径；lm为挤压起始长度；h1为前弹裙尺寸数据；φ为弹裙半锥角。

2 水柱质量变化模型和气体状态方程

水下锥膛炮与普通水下枪械的内弹道不同，主要体现在3个方面:一是射弹受到挤压阻力；二是变质量水柱的截面积是变化的；三是射弹弹后空间的体积变化不是等截面的。

2.1 膛内水柱质量变化模型

在内弹道过程中，射弹和弹前水柱在火药气体 作用下向前运动，由于锥膛炮分为3部分，射弹在相 同时间间隔排出水柱的体积也不相同，第1 直膛段 运动期间，水柱质量是3段质量之和; 锥膛段运动期 间，水柱为锥膛到第2 直膛之和; 第2 直膛段运动期 间，只排出直膛段的水。而水柱体积的变化是射弹 位移的函数，因此变质量水柱与位移的关系为

式中：ms为水柱质量；ρ为水密度；S1、S2分别为第1、第2直膛段截面积;R1、r1分别为截面积对应的半径；l1、l2、l3分别为第1直膛段、锥膛段和第2直膛段长度；lg为弹丸行程，即3段总长；ld为射弹长度；l为射弹位移；R=R1-(l-l1+ld)tanα。

2.2 变容状态方程

传统内弹道的变容状态方程[7]是等截面积的，而锥膛炮弹后空间截面是变化的，需要改进变容状态方程，即：

p(Vψ+Vd)=ωψkT

(6)

式中：药室自由容积Vψ=S1lψ，lψ为药室自由容积缩颈长；Vd表示弹后空间体积，是位移l的函数；Rh为射弹底部半径；ω为装药量；ψ为火药燃烧百分比；k为气体常数；T为温度。

3 水下锥膛炮内弹道方程组

3.1 形状函数和燃速方程

根据以上的推导可以得到水下锥膛炮内弹道方程组，其中形状函数采用三次式，燃速方程采用指数式[8]。形状函数为

(8)

燃速方程：

(9)

式中：Z为相对燃烧厚度;Zk为火药分裂点处相对燃烧厚度；x、λ、μ分别为火药形状特征量，由火药药形决定；χs、λs分别为多孔药分裂后的特征量；u1、n分别为燃烧系数和燃烧指数；e1为火药药厚一半。

3.2 运动方程

根据前面阻力和变质量水柱的公式，可知运动方程是一分段函数，将运动方程和能量方程分为3个阶段，不进行细致的划分。另外，水下射弹还受到出口动压力、静压力和水柱与枪管的摩擦力，文献[9]指出，静压力做功所消耗的火药能量很小，与动压力做功和水柱动能相比，相差两个数量级，故在水不是很深时可忽略水下静压力的影响。则射弹运动方程为

(10)

式中：FD为出口动压力；Ff为水柱与炮管的摩擦力；FZ为前后弹裙挤压阻力的合力，FZ=Fq+Fh，Fq、Fh分别为前、后弹裙挤压阻力；φ为次要功计算系数；ms1、ms2、ms3分别为各分段下水柱质量；p为压力；v为射弹速度。

3.3 能量方程

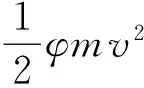
(11)

式中：Vd1、Vd2、Vd3分别为各分段下弹后空间体积；f为火药力；θ为火药热力系数。

至此，方程组(8)～(11)构成封闭可解的水下内弹道方程组，采用四阶龙格库塔法求解。

4 计算结果与分析

以某口径锥膛炮为例，当弹丸行程lg为1.9 m，采用7/14发射药对水下和空气中锥膛炮进行内弹道计算，其中水下内弹道参数如表1所示。

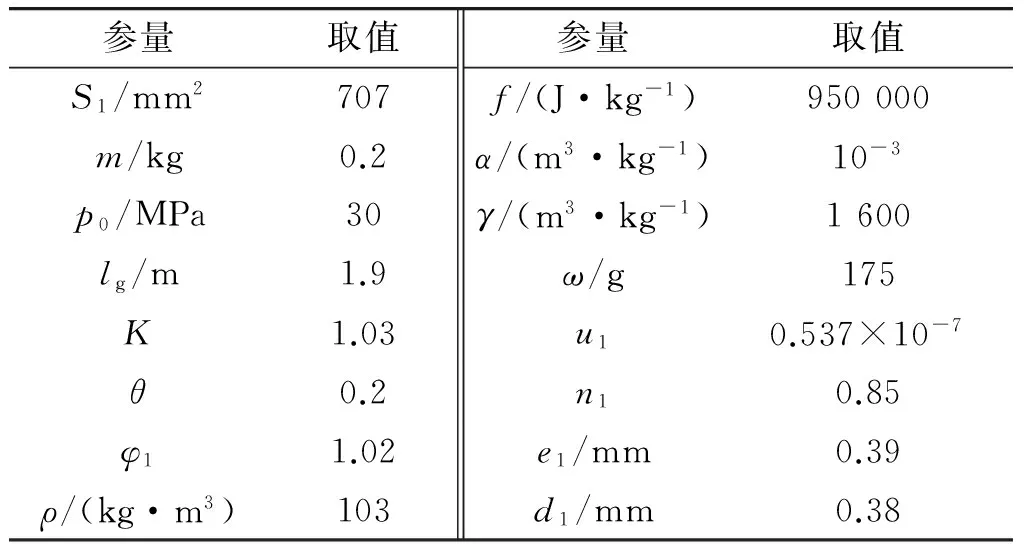
表1 水下内弹道参数

图3、4为锥膛炮在空气和浸水下的p-t和v-t曲线图。从图3中可看出，空气中最大压力为358 MPa，而水下压力曲线和文献[10]类似，最大压力处有“尖角”，最大压力为1 186 MPa，两曲线最大压力值相差很大，这是由于该身管尺寸过长，导致身管内水柱质量过大，可以计算出，水柱质量是射弹的3.5倍左右，起始时火药气体要推动射弹和比它重3.5倍的水柱，必然会增大膛内压强，所以在水下发射时，此压力值是不合适的，有必要修改身管尺寸，调整最大压力。

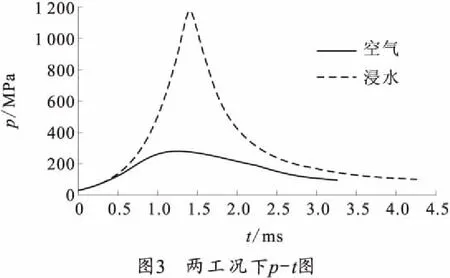
图4是两工况下的速度图，可以看到，在空气中射弹运动到炮口用时3.4 ms，炮口速度vg为1 035 m/s，这与文献[3]中实验测得的锥膛炮初速1 070 m/s相近，且和文献[8]中的同口径炮初速1 060 m/s相近。在水下射弹运动到炮口所用时间为4.3 ms，vg为626 m/s，相比之下，两者相差410 m/s，水柱的存在使射弹初速减小了39.5%且在内弹道过程后期，射弹速度在到达最大值后反而衰减。

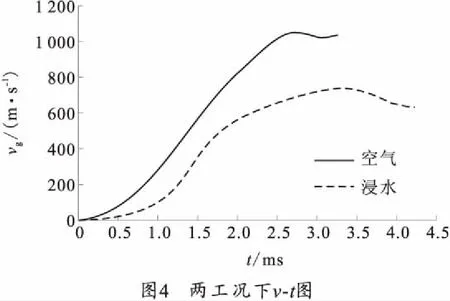
图4空气中的速度曲线在炮口附近存在一波谷，时间t=2.9 ms，对应位移l=1.5 m时，速度开始减小；在时间t=3.1 ms，对应位移l=1.65 m时，速度又渐渐增大，这与传统内弹道不相同。这是因为随着射弹向前运动，弹后空间逐渐增大，膛内压力减小，在2.9 ms时刻，压力小于挤压阻力，加速度变为负值，因此速度会减小。当射弹挤压成型后，挤压阻力消失，较小的膛压依然可以提供弹丸动力，推动弹丸前进，故在3.1 ms时刻，速度又渐渐上升一小段。

根据以上分析膛压过大的问题，将通过改变弹丸行程lg来调整身管长度，进而分析身管长度的影响。lg分别为0.7、0.8、0.9、1.0、1.2 m 5种工况下的最大膛压和炮口速度，如表2所示。

表2 5种工况下的最大膛压和初速

从表2中的炮口速度值可看出，lg为1.0 m对应的炮口速度较大，这与文献[10]得出的水下射弹炮口速度和身管长度存在最佳匹配的问题相一致。对比几种工况下的最大膛压，可看出改变lg，可以有效减小膛内最大压力值，lg为0.9、1.0和1.2 m时，膛压仍然比较大，均高于500 MPa，lg为0.7 m和0.8 m时，膛压比较接近，最大膛压在400～450 MPa之间。

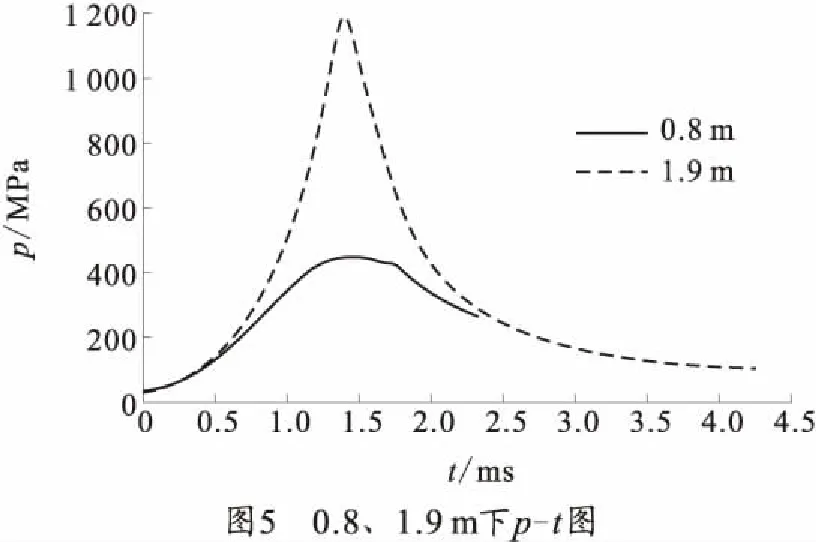
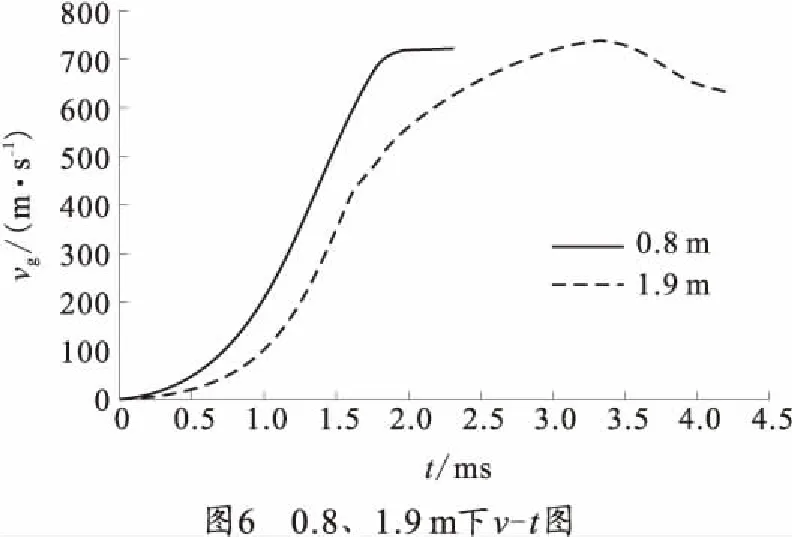
为研究浸水模式下身管长度对膛压及炮口速度的影响，以lg分别为0.8、1.9 m为例，计算出两工况下的膛压与炮口速度，如图5、6所示。可以看到lg为0.8 m的压力大幅度下降，且其炮口速度高于1.9 m的炮口速度，这是由于工况2的速度达到最大值后，射弹受到的阻力大于膛压而导致速度下降，低于工况1的速度。因此浸水模式下锥膛炮身管长度对膛压和炮口速度有影响，膛压随身管长度的增加而增大，炮口速度与身管长度存在最佳匹配关系。

5 结论

本文在锥膛炮空气中发射的基础上，基于挤压阻力、水柱质量变化和压力变化模型，推导出水下锥膛炮内弹道方程组。根据计算结果，得出以下结论：

1)空气中锥膛炮的射弹速度在接近炮口段时，由于挤压阻力和气体压力的共同作用，射弹速度会先下降后又上升一小段，这与传统内弹道不同。

2)水下锥膛炮的炮口速度与身管长度不成正相关，但其与身管长度之间存在最佳匹配的关系；身管长度尺寸影响膛内压力，膛压随身管长度的增加而增大。本文的研究为锥膛炮内弹道设计和弹炮匹配设计提供理论参考。

References)

[1]孔德仁,王昌明,柳光辽,等. 水下枪械内弹道分析及其理论建模[J]. 弹道学报,1998,10(3):1-5. KONG Deren, WANG Changming, LIU Guangliao, et al. Analysis of interior ballistic characteristics of underwater gun and theoretical model’s establishment[J]. Journal of Ballistics,1998,10(3): 1-5. (in Chinese)

[2]梁志峰,乔磊,姜驰. 基于MATLAB的空气炮内弹道仿真[J]. 河北农机,2015(12):62-64. LIANG Zhifeng, QIAO Lei, JIANG Chi. Interior ballistics simulation of air cannon based on MATLAB[J]. Hebei Farm Machinery，2015(12):62-64. (in Chinese)

[3]侯健,魏平,李金新. 锥膛炮内弹道建模与仿真计算[J]. 兵工学报,2010,31(4):419-422. HOU Jian, WEI Ping, LI Jinxin. Interior ballistics mode-ling and simulation of conic-chamber gun system[J]. Acta Armamentarii,2010,31(4):419-422. (in Chinese)

[4]郭锦炎,阮文俊,张丁山,等. 双药室小孔延时点火内弹道建模与试验研究[J]. 兵工学报,2011,32(10):1195-1199. GUO Jinyan, RUAN Wenjun, ZHANG Dingshan, et al. Interior ballistics modeling and experimental study on keyhole delayed ignition in double-chamber[J]. Acta Armamentarii,2011,32(10):1195-1199. (in Chinese)

[5]李淼,钱林方,陈龙淼. 弹带挤进过程内弹道特性研究[J]. 振动与冲击,2016,35(23):74-79. LI Miao, QIAN Linfang, CHEN Longmiao. Interior ballistics features during rotating band engraving process[J]. Journal of Vibration and Shock,2016,35(23):74-79. (in Chinese)

[6]魏平,侯健,陈汀峰. 基于锥膛炮的弹丸弹裙膛内阻力研究[J]. 兵工学报,2012,33(3):324-328. WEI Ping, HOU Jian, CHEN Tingfeng. Research on the bore resistance projectile sabots based on conic-chamber gun[J]. Acta Armamentarii, 2012, 33(3): 324-328. (in Chinese)

[7]金志明. 枪炮内弹道学[M]. 北京:北京理工大学出版社,2004:78-80. JIN Zhiming. Interior ballistics of guns[M]. Beijing:Beijing Institute of Technology Press,2004:78-80. (in Chinese)

[8]王连荣. 火炮内弹道计算手册[M].北京：国防工业出版社,1987:138-143. WANG Lianrong. Interior ballistics calculations of guns[M].Beijing:National Defense Industry Press, 1987:138- 143. (in Chinese)

[9]姚养无. 水下枪械内弹道基本方程组[J]. 火炮发射与控制学报,2006(1):6-9. YAO Yangwu. Fundamental equations for interior ballistic of underwater gun[J]. Journal of Gun Launch & Control,2006(1):6-9. (in Chinese)

[10]任成虎. 超空泡射弹内弹道特性规律研究[D]. 南京:南京理工大学,2009. REN Chenghu. Study on interior ballistics characteristics of supercavitating projectile[D]. Nanjing:Nanjing University of Science and Technology,2009. (in Chinese)