某迫击炮身管寿命分析及预测

杨 雕，陈志坚，刘朋科，曾志银，衡 刚

(1.西北机电工程研究所，陕西 咸阳 712099； 2.解放军边防学院，陕西 西安 710108)

身管寿命是指在火炮弹道性能降低到指标规定的允许值或发生疲劳破坏前身管所能发射的当量全装药射弹数，前者称为身管的弹道寿命，后者称为身管的疲劳寿命。身管寿命受其弹道寿命和疲劳寿命制约，其中较短者就是身管的寿命。

疲劳寿命是指零件或构件直至破坏时所作用的循环载荷的次数或时间。通常是指裂纹萌生寿命和裂纹扩展寿命的总和。从结构或材料受载开始，到形成初始裂纹，这一阶段称之为裂纹萌生阶段，载荷的循环次数称为裂纹萌生寿命；此后，扩展到临界裂纹长度为止的载荷循环次数称为裂纹扩展寿命[1]。

笔者以某迫击炮身管为研究对象，通过对炮钢及钛合金材料的疲劳性能试验，得到了两种材料在室温和高温下的静态材料参数以及断裂韧性参数。并建立身管结构有限元模型，仿真分析得到了身管结构在射击载荷作用下的应力应变。采用经典疲劳理论模型，研究获得了该迫击炮身管疲劳裂纹萌生和扩展寿命。依据国军标相关规定，确定了身管初速下降超过5%即为寿命终止的判定标准。以钛合金身管的4 925发实弹射击试验初速测试结果为依据，结合不同射击工况下的射弹数当量换算，建立了射弹发数与初速下降量的表征关系，最终预测了该炮使用钛合金材料身管的弹道寿命。

1 材料疲劳性能参数试验研究

1.1 静态拉压试验

对炮钢材料35CrMnNi2MoV和钛合金材料TC11在CSS4410型电子万能材料实验机上进行静态拉压试验。试验应变率为0.01 s-1，获得材料屈服极限和弹性模量如表1所示。

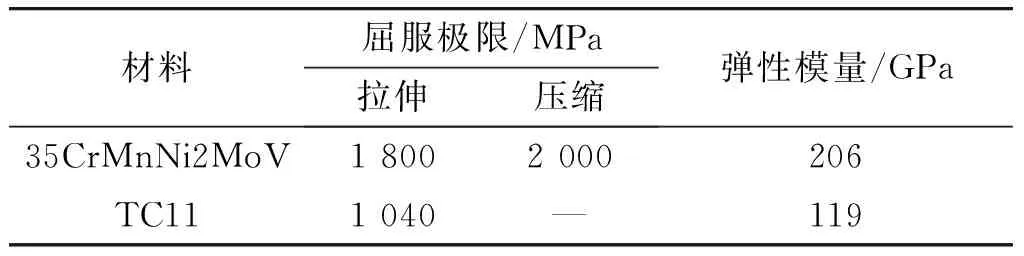
表1 材料静态拉伸、压缩试验结果

1.2 材料动态断裂韧度研究

材料的动态断裂韧度是材料在动态载荷下抵抗裂纹扩展的能力。由于火炮通常受动态载荷作用，其自身结构的微小裂纹在动态载荷作用下容易扩展，最终导致动态断裂。火炮身管裂纹受力符合I型(张开型)裂纹特征，因此针对两种材料I型裂纹断裂韧度进行了动态试验研究，为分析身管疲劳裂纹扩展寿命提供基础[2-3]。

I型动态断裂韧度试验利用Hopkinson压杆技术加载3点弯曲试样，以测试材料的动态断裂韧度。其基本原理是，由压缩空气炮将一圆柱形子弹以一定速度发射来撞击输入杆，在输入杆上产生压缩应力波，并沿输入杆向试样方向传播到输入杆与试样的界面时，一部分传播给试样，对试样施加冲击载荷；另一部分返回入射杆，形成反射波。输入杆上所贴的应变片可以完整地记录入射波、反射波，并由一维应力波理论可以确定施加给试样的载荷及加载点的位移随时间的变化情况。试样上所贴的应变片将测得试样上预制裂纹起裂时所产生的卸载波，并由之确定试样起裂时间[4]。试验装置的原理图如图1所示，装置图如图2所示。

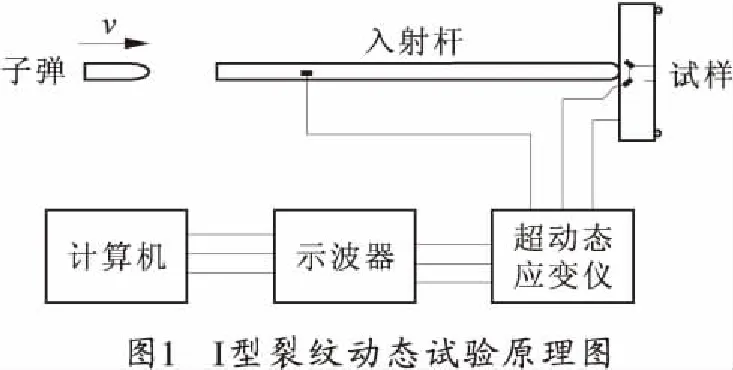
试验在测得了入射应变波εI及反射应变波后εR，可根据一维应力波理论求得输入杆与试样接触面处的位移u(t)及试样上的载荷p(t)，即：

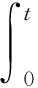
(1)

p(t)=E0A0(εI+εR)

(2)

式中：C0为入射杆的一维弹性波速，为5 189 m/s；E0、A0分别为入射杆的弹性模量及横截面积。

通过数值计算，计算出应力强度因子随时间的变化曲线。通过在试样上贴应变片的方法，将应变信号的最大值减去应力波从裂尖传播至应变片所需的时间作为起裂时间。找出起裂时间所对应的应力强度因子，即动态断裂韧度KIC。两种材料的动态断裂韧度如表2所示。

表2 两种材料的动态断裂韧度

2 身管疲劳裂纹萌生寿命估算

疲劳裂纹萌生寿命的研究方法主要有疲劳损伤累计理论、名义应力法、局部应力应变法、能量法等。火炮射击时身管受到类似脉动交变的疲劳载荷作用，具有大应变、高应力低周疲劳的特征，因此采用局部应力应变法进行疲劳裂纹萌生寿命分析[5]。

局部应力应变法是在大应变、高应力占主导地位的低周疲劳基础上发展起来的寿命估算方法，决定构件寿命的是应力集中处的最大局部应力和应变。该方法认为：若同种材料制成的构件的危险部位的应力-应变历程与一个光滑小试件的应力-应变历程相同，则寿命相同，此方法中局部应力和应变是控制参数。Manson-Coffin法是广泛应用的局部应力应变法之一,Manson-Coffin公式如下：

(3)

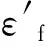
2.1 射击过程中身管应力应变分析

为了分析身管裂纹萌生寿命，首先需要得到身管在射击载荷作用下的应力及应变。因此，建立身管结构有限元模型，对炮钢和钛合金材料身管在强装药(最大膛压61MPa)与四号装药(最大膛压36MPa)下的应力应变进行了分析。身管内半径为41.03mm，外半径为47.05mm，长度取200mm，建模过程中，材料参数采用试验测得的参数。身管有限元网格和炮钢材料下四号装药等效应变分布图如图3所示。

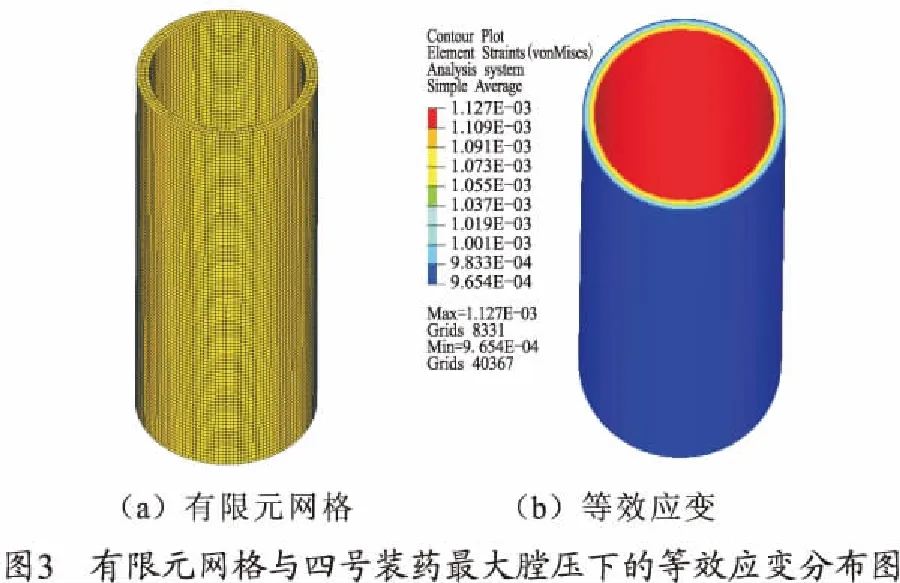
上述两种材料和载荷下的身管应变计算结果如表3所示。

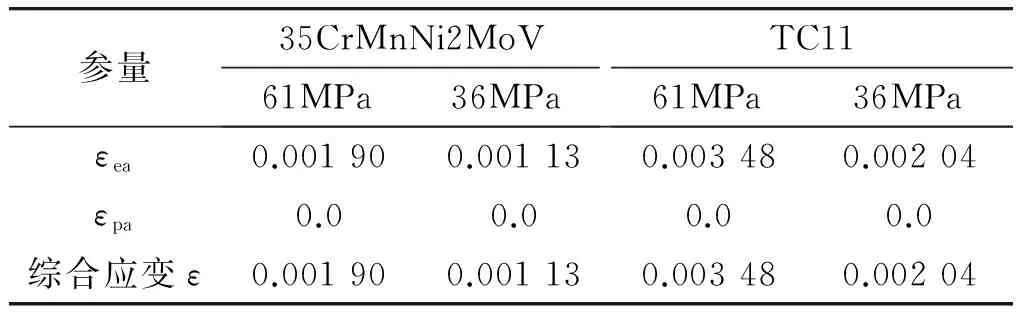
表3 身管应变计算结果

2.2 疲劳裂纹萌生寿命计算

表4 不同材料及压力下身管裂纹萌生寿命

3 身管疲劳裂纹扩展寿命估算

在裂纹长度达到临界裂纹尺寸ac以前，疲劳裂纹扩展缓慢，而疲劳裂纹扩展速率就是指这一阶段的快慢。将每次载荷循环中裂纹的增量为da/dNp，称为裂纹扩展速率。帕瑞斯(Paris)分析了大量的试验结果后，给出了裂纹扩展速率的经验公式[6]为

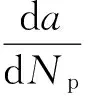
(4)

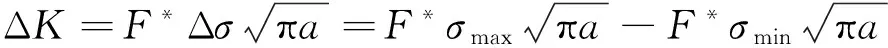
(5)

式中： ΔK是应力强度因子幅值；C、m分别为材料常数；a为裂纹尺寸；Np为交变载荷的循环次数；σmax、σmin分别为最大和最小应力；F*是与裂纹的形状、位置、加载方式及结构的几何形状有关的系数。

故：

(6)

式中：ai为初始裂纹深度；ac为临界裂纹深度。

临界裂纹尺寸可由材料断裂韧度求得。

(7)

设身管承受内压为p,并在内表面有一沿轴向的椭圆形表面裂纹，如图4所示。

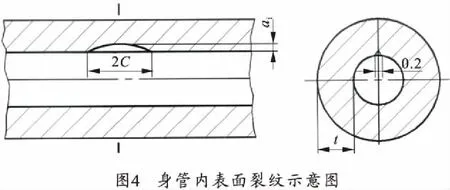
身管内半径r=41.03 mm，外半径R=47.05 mm，裂纹初始深度ai=0.2 mm。身管内表面切向最小应力为0，最大应力为[7]：

(8)

Δσ=σθmax-σθmin

(9)

炮钢材料相关裂纹扩展分析参数为:KIC=55.8 MPa·m1/2，F=1.2，C=2.13×10-11，m=3.18；钛合金材料相关参数为KIC=46.6 MPa·m1/2，F=1.2，C=1.02×10-10，m=2.785。

根据上述参数，通过疲劳裂纹扩展寿命公式，计算出不同材料和压力下的身管裂纹扩展寿命Np,如表5所示。

表5 不同材料及压力下身管裂纹扩展寿命

身管疲劳寿命即为裂纹萌生寿命和裂纹扩展寿命之和。故身管疲劳寿命如表6所示。

表6 不同材料及压力下身管疲劳寿命

4 身管弹道寿命预测

根据国军标GJB 2975—1997 火炮寿命试验方法中关于身管寿命的评定标准，并结合以往服役过程中该迫击炮射弹发数与其性能的定性关系。将初速下降5%作为该迫击炮寿命终止条件。

试验在钛合金材料身管下进行，射弹均为四号装药，实弹射击总发数为4 921发，实弹射击测试获得的初速与射击发数关系如图5所示，图中y为初速，x为射击发数。

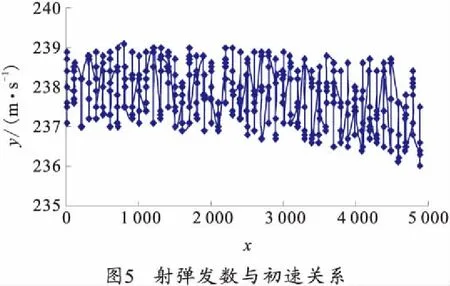
由于射击发数是有限的，为了获得初速和射击发数的关系，采用数据拟合处理方法，对初速数据和射击发数进行多项式曲线拟合，得到初速和射击发数相对应的表征关系式，以此预测身管寿命。多项式曲线拟合采用如下数学模型：

(10)

式中，b和ci分别为常量。

对所测试的初速数据和射击发数分别采用2次、3次多项式进行拟合，获得的拟合曲线如图6所示。

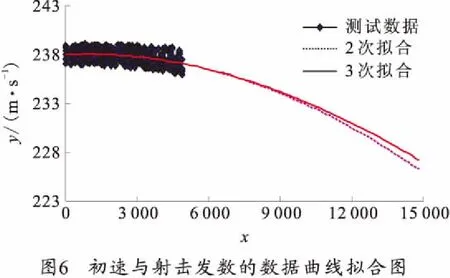
采用2次方程拟合得到的初速与射击发数关系式为

y=-6.045 950 50×10-8x2+1.117 718 60×10-4x+238.0

(11)

采用3次方程拟合得到的初速与射击发数关系式为

y=5.323 446 36×10-13x3-6.439 459 66×10-8x2+1.194 734 88×10-4x+238.0

(12)

将初速下降5%作为该炮的弹道寿命终止条件，即初速从238.0 m/s下降到226.1 m/s。通过对二次曲线计算，可以推断某迫击炮钛合金身管在发射四号装药时的弹道寿命约为14 986发。

火炮寿命试验规定以寿命终止前所发射的等效全装药弹数为标准。由于本次试验均采用四号装药进行射击，故射弹发数应当乘以等效全装药系数kEFC:

kEFC=(Pm/Pma)1.4(v0/v0a)

(13)

式中：Pm为等效装药膛内压力;Pma为全装药膛内压力;v0为等效装药的初速;v0a为全装药的初速。

通过计算得kEFC=0.382 497，故全装药射弹发数为

Faa=Fa4×kEFC=5 732

(14)

式中:Faa为全装药射弹发数;Fa4为四号装药射弹发数。

因此，由前述建立的初速与射弹发数关系式预测，对于钛合金身管，弹道寿命终止时，对应四号装药射弹发数约为14 986发，对应全装药射弹发数约为5 732发。

5 结论

笔者以某迫击炮为研究对象，针对身管材料由炮钢更换为钛合金后的身管寿命问题，采用经典疲劳理论模型，研究获得了该迫击炮身管使用炮钢和钛合金材料时不同装药量的疲劳寿命。即使用炮钢材料强装药下疲劳寿命24 721发，四号装药下疲劳寿命657 618发；使用钛合金材料强装药下疲劳寿命为30 080发，四号装药下疲劳寿命为696 095发。然后以4 925发实弹射击试验初速测试结果为依据，建立了射弹发数与初速下降量的表征关系，预测该迫击炮使用钛合金材料身管在全装药下的弹道寿命为5 732发。

References)

[1]李舜酩.机械疲劳与可靠性设计[M].北京:科学出版社，2006. LI Shunming. Mechanical fatigue and reliability design[M]. Beijing: Science Press, 2006. (in Chinese)

[2]黄克智,余寿文.弹塑性断裂力学基础[M].北京:清华大学出版社,1985. HUANG Kezhi, YU Shouwen. Foundation of elastic plastic fracture mechanics[M]. Beijing: Tsinghua University Press,1985. (in Chinese)

[3]范天佑.断裂动力学原理与应用[M].北京:北京理工大学出版社,2006. FAN Tianyou. Principle and application of fracture dyna-mics[M]. Beijing: Beijing Institute of Technology Press, 2006. (in Chinese)

[4]崔新忠,范亚夫,纪伟,等.用Hopkinson杆技术研究材料动态断裂韧性的进展[J].兵器材料科学与工程,2010,33(2)：118-122. CUI Xinzhong, FAN Yafu, JI Wei, et al. Progress in the research of dynamic fracture toughness based on Hopkinson bar technique[J]. Ordnance Material Science and Engineering, 2010,33(2)：118-122. (in Chinese)

[5]黄宁.大型结构件的疲劳寿命预测方法研究[D].长沙：中南大学,2013. HUANG Ning. Research on fatigue life prediction methods for large-scale components[D]. Changsha: Central South University,2013. (in Chinese)

[6]张纪奎,吴烈苏,马少俊,等.航空铝合金弹塑性状态疲劳裂纹扩展速率试验[J].北京航空航天大学学报,2013,39(9)：1218-1221. ZHANG Jikui, WU Liesu, MA Shaojun, et al. Experimental studies on fatigue crack growth rate at elastic-plastic state of aeronautical aluminum alloy[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013,39(9)：1218-1221. (in Chinese)

[7]曾志银,张军岭,吴兴波.火炮身管强度设计理论[M].北京:国防工业出版社,2004. ZENG Zhiyin, ZHANG Junling, WU Xingbo. Strength design theory on gun tube[M]. Beijing: National Defense Industry Press, 2004. (in Chinese)