基于神经网络与改进证据理论融合的故障诊断方法

刘保杰，杨清文，吴 翔，房施东

(陆军军官学院 五系，安徽 合肥 230031)

随着高新技术在常规兵器中的广泛应用，火箭炮随动系统控制原理更先进，控制系统精度更高，根据驱动元件的不同，伺服控制系统可分为机电伺服控制系统、气动伺服控制系统和液压伺服控制系统三大类。液压驱动的火箭炮随动系统具有体积紧凑、平稳性好及功率强等特点，在武器系统中得到了广泛应用[1]。由于液压系统故障具有故障点隐蔽，故障因果关系复杂，在实际诊断过程中存在许多不确定因素。目前，液压系统故障诊断采用的方法，主要有遗传算法、神经网络、模糊理论、粒子群算法以及它们的融合等[2-7]，但在实际故障诊断过程中时常出现不同方法对同一故障的诊断结果不一致的情况。这就需要采用一种方法对不同诊断结果进行融合，从而得出正确的结论。

证据理论是一种基于非精确推理的信息融合方法，它可以将不同数据源的信息进行有效综合，并在液压系统的故障诊断中得到了广泛应用[8-11]。但是，证据理论的基本可信度分配过于依赖专家的主观化赋值，不同的专家对同一个命题的证据可能给出差别很大的信度分配。同时，当证据间存在高度冲突时，D-S证据理论的合成结果可能有悖于常理。

因此，笔者在对证据理论研究的基础上，提出将神经网络和证据理论两者有机结合的诊断方法，将神经网络的输出值处理后作为D-S证据理论辨识框架上命题的基本可信度，实现了证据理论基本可信度赋值的客观化，并对D-S证据理论的合成规则进行改进，使其处理冲突证据的能力得到增强。试验证明可大大提高故障诊断的确诊率。

1 液压系统故障诊断模型

笔者提出的液压系统故障诊断的主要思想：对液压驱动的火箭炮随动系统的故障征兆以及常见的故障进行收集，组成故障样本；在此基础上构造了两个BP神经网络分别处理铁谱数据和压力、流量、温度(YLW)等数据，其中，铁谱数据是通过定量和定性分析从油液中分离的磨损微粒的成分、浓度、尺寸特征和污染物微粒的材质及化学成分得到，YLW数据是通过安装在液压元件上的压力、流量和温度传感器获得，进行故障的局部诊断，避免了单个BP神经网络复杂的结构形式，减少了BP网络训练时间，克服了因某一传感器故障或数据源错误造成的系统故障误诊；将处理后的两个BP神经网络的输出值作为D-S证据理论辨识框架上命题的基本可信度，实现赋值的客观化，然后，利用D-S证据理论进行融合，从而得到融合后最终的故障诊断结果。该诊断系统分为数据预处理模块、BP神经网络的局部诊断模块和D-S证据理论的全局诊断模块三大模块。诊断系统模型如图1所示。

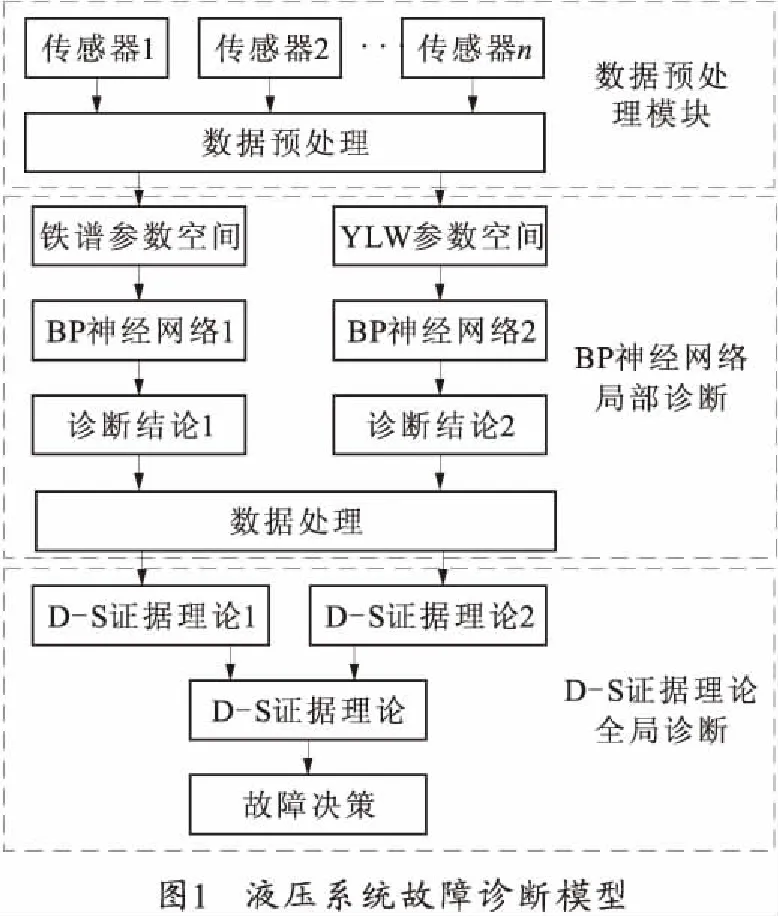
1.1 数据预处理

两个神经网络的输入数据是不同的物理参数，各个物理参数的量值不尽相同。若输入数据的绝对值过大，将导致BP神经网络输出饱和，进而使误差对权值的变化不太敏感，所以，在对BP神经网络训练之前，通过归一化处理，使输入数据的范围在[0，1]之间。考虑到压力、流量、温度和铁谱浓度量程相差较大，在归一化处理时，本文采用归一化公式如下[10]：

Yij=(Xij-Xjmin)/(Xjmax-Xjmin)

(1)

式中：Yij为输入数据归一化后的输出；Xjmax和Xjmin分别为第j个特征分量的最大值和最小值；Xij为第i个样本的第j个特征分量。

1.2 D-S证据理论及其改进

1.2.1 D-S证据理论相关概念

D-S证据理论可以用来融合来自多信息源(传感器)的相容命题，并对这些相容命题的交集(合取)命题所对应的基本信任分配函数赋值。

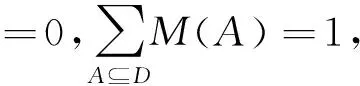
0，则A为证据的焦元。

定义2：设M1，M2,…，Mn为基本可信度分配函数，则D-S证据理论的合成规则为

(2)

(3)

式中，K表示证据之间的冲突程度，其值越大对最终合成结果的影响越大。

定义3：设辨识框架D上有证据体n个，焦元m个，若证据体i对焦元A的基本可信度Mi(A)与大多数证据体对焦元A的基本可信度存在较大差异，则称证据体i对应的焦元Ai为焦元集A中的矛盾焦元。

1.2.2 改进的D-S证据理论算法

为解决证据间高度冲突导致合成结果有悖于常理的问题，引入距离函数的概念用以表示证据间的差异性，重新定义冲突系数并引入信任系数的概念。

定义4：设样本空间D包含n个不同命题，Mi，Mj为D上的两个基本可信度分配函数，那么，Mi，Mj的距离可表示为[12]

(4)

式中，F为一个2n×2n的矩阵

定义5：证据i,j的冲突系数为

(5)

改进冲突证据的合成算法步骤为：

1)判断样本空间D中是否存在矛盾焦元，若不存在，按式(2)计算融合后的基本可信度；否则执行步骤2)。

2)按式(3)、(4)分别计算冲突程度系数K和证据距离d。

4)计算信任系数：α=1-Kd。

5)对按照式(2)计算的融合结果M(A)进行修正：M′(A)=αM(A)。若有多个证据，需将M′(A)与其他证据进行再次合成，如此循环进行。

1.3 BP神经网络及其改进

BP神经是一个单向传播的多层前馈网络，其分为3层(输入、隐含和输出层)，同层节点之间没有连接，相邻层采用全互连方式连接，不相邻层之间没有直接联系。图2是BP神经网络的拓扑结构。

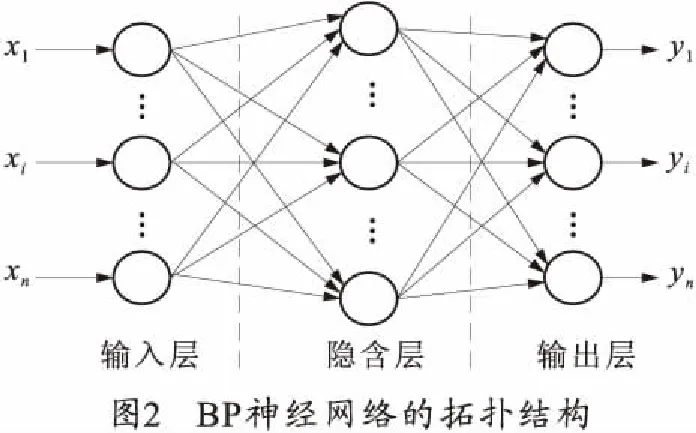
1.3.1 BP神经网络的算法改进

标准BP算法按t时刻的梯度下降方向调整权值，t时刻以前的梯度方向则不予考虑，有时会导致训练收敛速度慢及系统振荡，甚至出现误差梯度局部最小。为了解决标准BP算法的这种弊端，引入动量项的概念，用以改善系统的收敛性，减少学习过程的振荡，其原理是加入一动量项β∈[0,1]。其权值修正公式为[4]

wij(k+1)=wij(k)+η[(1-β)D(k)+βD(k-1)]

(6)

式中：D(k)表示k时刻的负梯度；D(k-1)表示k-1时刻的负梯度；η为学习率。

当β=0时，权值修正完全取决于当前负梯度；当β=1时，权值修正只与上一次循环的负梯度有关，β一般取0.95。

1.3.2 隐含层节点数选择

从样本中提取并存储样本内在规律是BP网络中隐含层节点的作用，BP网络获取样本信息的能力与隐含层节点数密切相关，节点数量太少，获取的信息不能反映样本规律；节点数太多，可能出现“过度吻合”，掌握了样本中非规律性的内容，增加了训练时间，降低了泛化能力。

试凑法是确定隐含层节点数的常用的方法，试凑法的初始值通过隐含层节点数的经验公式获得，通过训练确定最终的隐含层节点数。针对只用3层的人工神经网络，确定隐含层节点数常用的经验公式有：

(7)

m=log2n

(8)

(9)

式中：n为输入层节点数；m为隐含层节点数；l为输出层节点数；c为1～10之间的常数。

通过仿真实践发现，按式(8)和(9)计算隐含层节点数，往往不能使训练误差最小，而按式(7)使用试凑法计算，一般都能取得很好的效果，因此，本文选择式(7)计算隐含层节点数。

2 诊断实例

为了验证神经网络和证据理论集成的故障诊断方法的有效性，笔者依托某大学的液压综合试验台搭建液压驱动火箭炮随动系统作为试验对象，采用模拟液压泵故障作为被诊故障。该液压驱动火箭炮随动系统包括方向机液压系统，高低机液压系统，具有调炮、跟踪和精确瞄准目标的功能，其结构主要由滤油器、溢流阀、液压泵、压力表、单向阀、电液比例方向阀(配套放大器)、液压缸、液压缸、位移传感器、压力传感器、数据采集卡和工业控制计算机组成。液压驱动火箭炮随动系统原理图如图3所示。

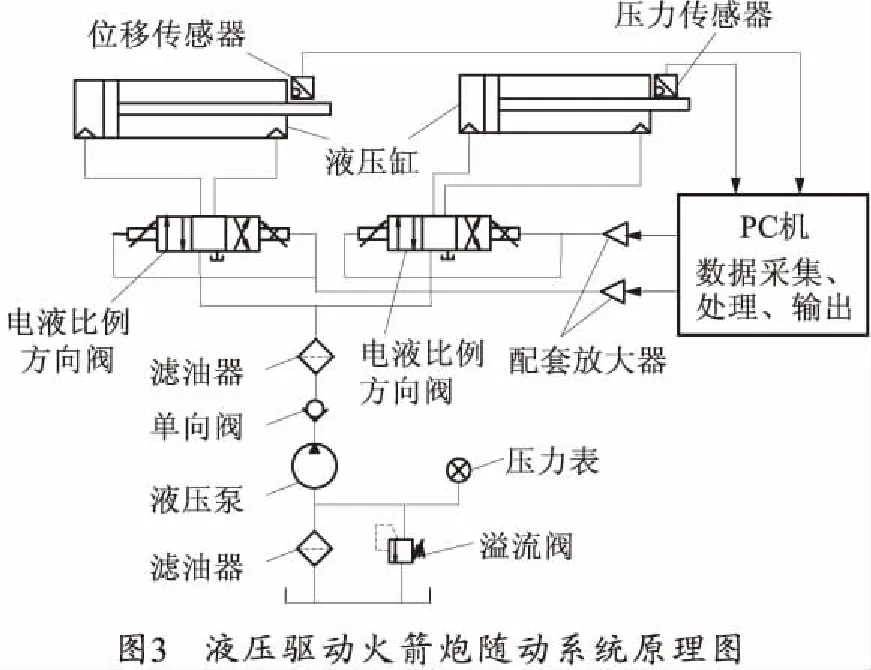
2.1 特征向量的确定和样本数据的收集

2.1.1 输入、输出特征向量的确定

BP神经网络1用于处理铁谱数据，将磨粒的成分、浓度、尺寸特征以及其他污染颗粒的成分4个参数作为输入层的特征向量。在BP神经网络2中，根据液压驱动火箭炮随动系统在实际工作中常出现的故障现象，选取液压油液温度、液压泵出油口压力、液压缸进油口压力、液压缸出油口压力、液压泵出油口流量和液压缸出油口流量9个参数作为网络2的输入特征向量。输出层的5个节点输出分别为：吸油滤油器堵塞F1、液压泵故障F2、液压油缸泄漏F3、电液比例方向阀故障F4、溢流阀故障F55种常见的系统故障类型。

2.1.2 样本数据的收集

采集液压系统分别工作在1～10 MPa压力下，正常工作和发生液压泵故障时铁谱数据和压力、流量、温度(YLW)信号作为诊断数据。对神经网络1和神经网络2分别取5 MPa时200组铁谱数据和YLW信号，其中150组数据作为诊断网络训练数据，50组数据作为诊断数据。

2.2 基于 Matlab 的网络仿真

2.2.1 隐含层节点数的选择

将采集到的200组样本数据输入到两个BP神经网络。基于MATLAB平台的神经网络模块对网络进行训练，参数设置如下：训练函数为trainscg，学习率η为0.94，训练精度为0.001，输出层传递函数和隐含层传递函数分别使用 S 型的对数函数和正切函数。按照隐含层节点数经验公式(7)计算两BP神经网络的隐含层节点数m，可以得到m∈[4，13]。然后，计算两个BP神经网络在达到同等训练精度情况下，不同隐含层节点数的的训练次数和识别率，如表1所示。根据训练结果，确定BP神经网络1的网络结构为4×12×5，BP神经网络2的网络结构为9×13×5。此时，网络收敛速度较快，正确识别率较高。但是，两个神经网络的识别精度存在差异。

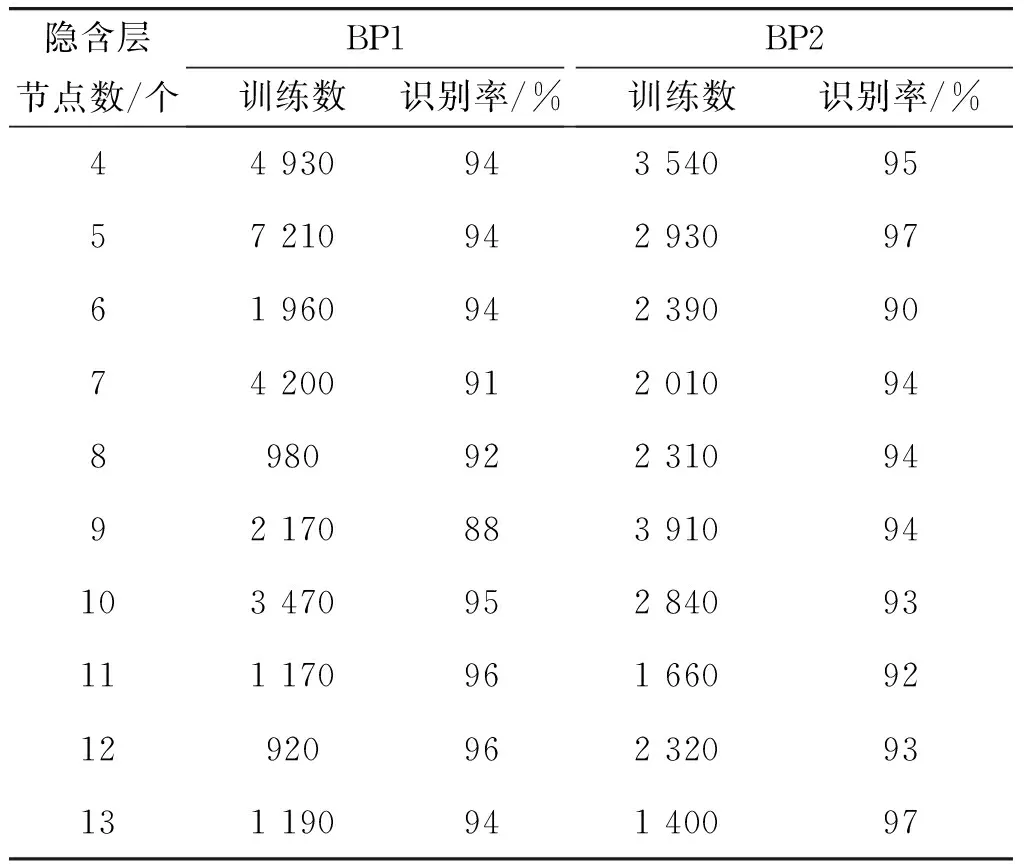
表1 BP网络训练次数和识别率

2.2.2 输出结果

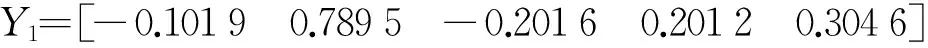
2.3 D-S证据理论独立诊断及合成诊断

2.3.1 识别框架

液压系统的识别框架D={F1,F2,F3,F4,F5}，命题F1表示吸油滤油器堵塞；F2表示液压泵故障；F3表示液压油缸泄漏；F4表示电液比例方向阀故障；F5表示溢流阀故障。

2.3.2 基本概率分配

分别将两个BP神经网络输出值按照如下公式进行处理，作为各焦点元素的基本概率，其计算公式为

(10)

式中:αx为诊断网络的可靠性系数;M(Fi)为各焦元的基本概率;y(Fi)为神经网络的实际输出;Fi为5个输出特征量的第i种故障模式。

诊断网络的不确定性信度分配计算公式为

M(D)=1-αx

(11)

网络的诊断可靠性系数αx是通过向两个训练好BP神经网络输入测试数据得到，这里分别取0.85和0.92。

按公式(10)对输出结果进行处理，得到独立诊断的诊断结果，然后按照上文1.2节提出的改进冲突证据的合成算法将独立诊断结果进行合成，得到合成后的诊断结果。独立诊断的诊断结果和合成诊断结果如表2所示。

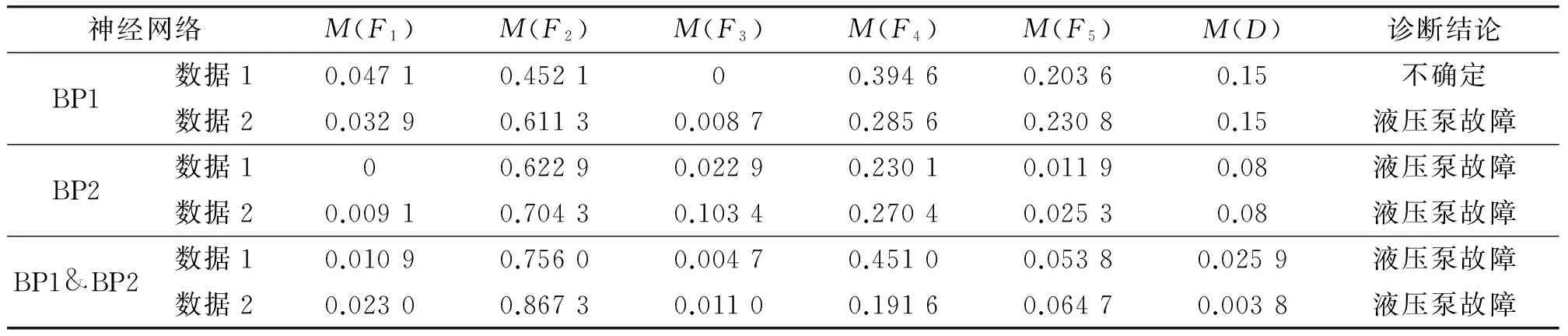
表2 两个BP网络以及证据理论合成后的诊断结果

对诊断结果，可采用最大信任度值法做出决策判断。设F1，F2⊂D,且M(F1)=max{M(Fk),Fk⊂D},M(F2)=max{M(Fk),Fk⊂D,且Fk≠F1}，若满足

(12)

则F1为识别的故障类型，ε1，ε2为预先设定的阈值。根据实际设置的液压泵故障诊断情况,经大量仿真试验后将ε1，ε2分别确定为0.3和0.18。

由表2可以看出，在铁谱诊断网络(BP1)中，M(F2)=0.452 1，M(F4)=0.394 6，诊断网络无法分辨系统是液压泵故障还是控制阀故障，处理冲突证据的能力不强，另外，由于液压泵使用材料和控制阀使用材料基本相同，使用铁谱数据也不易对其进行故障区分。YLW诊断网络(BP2)选择压力、流量、温度作为诊断数据，液压泵故障对流量，压力影响比较明显，因此，YLW诊断网络能够很好的确诊故障。但其不确定性信度M(D)比较高，达到了0.08。为提高诊断的准确率，充分利用不同证据的冗余和互补故障信息，采用改进的证据理论对两个BP神经网络的诊断结果进行融合处理，可以发现，故障状态的信度分配明显凸显，实现了系统故障状态的精确识别，不确定性信度分配M(D)也明显减小，仅为0.025 9，对冲突证据的诊断能力明显增强。

3 结论

由于液压元器件所用材料存在很大的相似性，铁谱分析在对故障进行精确定位上存在一定的局限性，但其与其他参数结合能很好的实现故障诊断。

将液压系统的原始特诊参数分类后，利用神经网络分别进行处理，以基于信任因子的合成方法对神经网络的输出结果进行合成，可实现对冲突证据有效合成，能明显提高故障分类识别精度。

采用两个并行的神经网络与单个神经网络和证据理论融合的故障诊断方法相比，简化了神经网络结构，提高了局部诊断网络的诊断效率，实现了证据理论的基本可信度分配赋值的客观化，可以使故障状态的信度分配明显凸显，提高故障诊断的可靠性。

References)

[1]周文驰．火箭炮随动装置液压控制系统研究[D]．武汉：武汉科技大学，2014：7-12． ZHOU Wenchi. The research of servo hydraulic control system of the rocket follow up device[D]. Wuhan: Wuhan University of Science and Technology, 2014: 7-12.(in Chinese)

[2]沈美杰，赵龙章，周兵，等．基于PSO优化的RBF网络液压泵故障诊断研究[J]．液压与气动，2016(5)：87- 92． SHEN Meijie, ZHAO Longzhang, ZHOU Bing, et al. Hydraulic pump fault diagnosis of RBF network based on PSO optimization[J]. Chinese Hydraulics & Pneumatics, 2016(5):87-92.(in Chinese)

[3]刘小平，鄂东辰，高强，等．基于BP神经网络的翻车机液压系统故障诊断[J]．液压与气动，2016(8)：68-73． LIU Xiaoping, E Dongchen, GAO Qiang, et al. Fault diagnosis based on BP neural network for hydraulic control system of rotary dump[J]. Chinese Hydraulics & Pneumatics, 2016(8):68-73.(in Chinese)

[4]曹凤才，岳凤英．基于BP神经网络的液压系统故障诊断研究[J]．中北大学学报：自然科学版，2010,31(6)：596- 599． CAO Fengcai, YUE Fengying. Fault diagnosis of hydraulic system based on BP neural network[J]. Journal of North University of China:Natural Science Edition,2010,31(6):596-599.(in Chinese)

[5]宋星，杨彦青，金珍珍．基于模糊故障诊断算法的米巴赫焊机液压伺服系统监测与故障诊断系统[J]．电焊机，2014，44(9)：68-71． SONG Xing, YANG Yanqing, JIN Zhenzhen. Research on the monitoring and fault diagnosis system for hydraulic servo system of Miebach welding machine based on the fuzzy fault diagnosis algorithm[J]. Electric Welding Machine, 2014，44(9):68-71.(in Chinese)

[6]游张平，江洁，胡小平，等．起重机液压系统的粒子群神经网络故障诊断[J]．液压与气动，2014(1)：114-118． YOU Zhangping, JIANG Jie, HU Xiaoping, et al. Fault diagnosis methods for crane hydraulic system based on particle swarm neural network[J]. Chinese Hydraulics & Pneumatics, 2014(1):114-118.(in Chinese)

[7]宋涛，舒涛，雷荣强，等．基于蚁群神经网络的发射系统故障诊断[J]．火力与指挥控制，2015，40(9)：143-146，151． SONG Tao, SHU Tao, LEI Rongqiang, et al. Research on fault diagnosis for launch system based on ant colony neural network[J]. Fire Control & Command Control, 2015, 40(9):143-146,151.(in Chinese)

[8]JOUSSELME A L, GRENIER D, BOSSE E. A new distance between two bodies of evidence[J]. Information Fusion, 2001,2(2):91-101.

[9]张旭婧，董增寿．修正的D-S证据理论在液压故障诊断中的应用[J]．太原科技大学学报，2011，32(5)：370- 373． ZHANG Xujing, DONG Zengshou. Modified D-S evidential theory in hydraulic system fault diagnosis[J]. Journal of Taiyuan University of Science and Technology, 2011,32(5):370-373. (in Chinese)

[10]刘希亮，陈桂明,李方溪．基于改进证据理论的多传感器信息融合故障诊断[J]．中国机械工程，2014，25(10)：1341-1345． LIU Xiliang, CHEN Guiming, LI Fangxi, et al. Multi-sensor information fusion fault diagnosis based on improved evidence theory[J]. China Mechanical Enginee-ring, 2014,25(10):1341-1345.(in Chinese)

[11]DONG Zengshou, ZHANG Xujing. Modified D-S evi-dential theory in hydraulic system fault diagnosis[J]. Procedia Environmental Sciences, 2011,11(Part A):98-102.

[12]蒋雯，张安，邓勇．基于新的证据冲突表示的信息融合方法研究[J]．西北工业大学学报，2010，28(1)：27- 32． JIANG Wen, ZHANG An, DENG Yong. A novel information fusion method based on new evidence conflict representation[J]. Journal of Northwestern Polytechnical University, 2010,28(1):27-32. (in Chinese)