Lebesgue积分变量替换和分部积分的应用
2017-01-17柳彦军
柳彦军
(重庆第二师范学院 数学与信息工程系,重庆 400067)
Lebesgue积分变量替换和分部积分的应用
柳彦军
(重庆第二师范学院 数学与信息工程系,重庆 400067)
通过Lebesgue积分变量替换和分部积分,得到了一些相关结论,并给出了一些具体的应用实例.
勒贝格积分;变量替换;分部积分
0 引 言
与黎曼积分类似,勒贝格积分也可以进行变量替换和分部积分,需要在一定的条件下进行[1].但目前勒贝格积分变量替换和分部积分的文献很少,本文的创新之处在于,给出了勒贝格积分变量替换和分部积分的应用,通过典型的实例说明勒贝格积分在应用方面的优势,一方面,这是积分理论的深化,另一方面,这些内容在实变函数的教学改革中有重要意义.
1 勒贝格积分的变量替换和分部积分

另一方面,
当x→0时极限不存在,所以f(x)在x=0处不可导[2],但有如下重要定理:
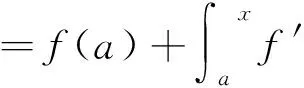
定理2[4](勒贝格积分的变量替换) 设f(x)在[a,b]上L可积,φ(t)是在[α,β]上严格单调递增的绝对连续函数,且φ(α)=a,φ(β)=b,则f(φ(t))φ′(t)作为t的函数在[α,β]上L可积,且
定理3[4](勒贝格积分的分部积分法) 若f(x)和g(x)都在[a,b]上绝对连续,则
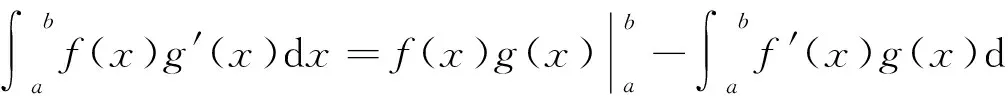
2 勒贝格积分变量替换与分部积分的应用
通过前面得出了在绝对连续的条件下勒贝格积分能进行变量替换与分部积分[5],下面通过一些实例说明其运用.
2.1 勒贝格积分变量替换的应用
例1 设f在[a,b]上的绝对连续函数,若有f([a,b])=[c,d],证明:对[a,b]中的波雷尔集,必有
证明对任一区间[p,q]⊂[c,d],记r=f-1(p),s=f-1(q),则
因为f′∈[a,b],故命题得证.
2.2 勒贝格分部积分的应用

证明令
且有
所以得到
现在,根据多项式一致逼近连续函数的定理,可知对任意的ε>0,存在多项式P(x),使得

注意到
有
从而可知
由ε的任意性可得F(x)≡0,于是得f(x)=0.
例3 讨论函数
当β>0时的绝对连续性.
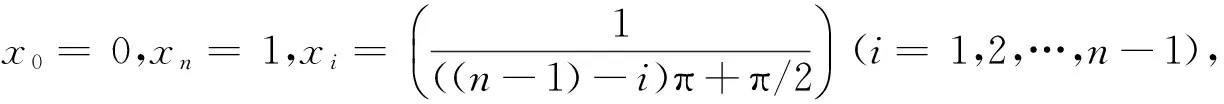
又
所以,当α≤β时,f(x)在[0,1]不是绝对连续函数.

事实上,
3 结论与认识
为了使定积分的计算更简单,本文通过黎曼积分引入勒贝格积分的变量替换和分部积分,并详细论述其应用,扩大勒贝格积分的使用范围,弥补黎曼积分在计算上的一些不足.
[1]夏道行,吴卓人,严绍宗,等.实变函数论与泛函分析:上册(2)[M].北京:高等教育出版社,2010:169-170.
[2]华东师范大学数学系.数学分析:3[M].北京:高等教育出版社,2001:89-90.
[3]周明强.实变函数论[M].北京:北京大学出版社,2014:195-200.
[4]程其襄,张奠宙,魏国强,等.实变函数论与泛函分析基础:3[M].北京:高等教育出版社,2010:162-168.
[5]孙雨雷,冯君淑.实变函数论与泛函分析习题全解:上[M].北京:中国水利水电出版社,2011:87-88.
Application of Lebesgue Integral Variable Substitution and Integration by Parts
LIU Yanjun
(Departmentofmathematicsandinformationengineering,ChongqingUniversityofEducation,Chongqing400067,China)
Through the Lebesgue integral variable substitution and integration by parts,some relevant conclusions are derived,and some specific examples of application is presented.
Lebesgue integral; variable substitution; integration by parts
2016-09-01
重庆第二师范学院校级青年项目(KY201548C)
柳彦军(1988—),男,甘肃庄浪人,重庆第二师范学院数学与信息工程系讲师.
10.3969/j.issn.1007-0834.2016.04.015
G642.0;O174.1
1007-0834(2016)04-0061-03
