组合梁钢与混凝土界面连接效应的精细化计算

苏庆田， 薛智波， 李晨翔， 姜 旭

(1.同济大学 土木工程学院，上海 200092； 2.上海市政交通设计研究院有限公司，上海 200030)

组合梁钢与混凝土界面连接效应的精细化计算

苏庆田1， 薛智波1， 李晨翔2， 姜 旭1

(1.同济大学 土木工程学院，上海 200092； 2.上海市政交通设计研究院有限公司，上海 200030)

为定量了解组合梁桥中钢与混凝土界面上各种连接效应的作用，提出一种能够考虑钢与混凝土界面上包括连接件效应、黏结效应和摩擦效应的计算分析方法，通过试验验证该方法是可行的.利用该方法计算分析了组合梁中不同连接效应对组合梁应力及钢与混凝土界面滑移的影响，也研究了考虑钢与混凝土界面黏结效应与否对组合梁各部分构件受力的影响,得知钢与混凝土界面黏结效应对组合梁中钢梁和混凝土的受力影响较少，但对连接件剪力影响较大，在不同荷载作用下剪力降低最大可达到25%.

组合结构； 分析方法； 黏结； 连接件； 非线性有限元

钢与混凝土组合梁通过界面上的黏结作用、摩擦、机械咬合作用及结构连接件等实现钢与混凝土间的传力，保证组合结构各部分的协同受力[1-3].过去计算分析组合梁钢与混凝土界面上的连接效应基本上是不可能的，而且测试这种连接效应也十分困难，因此在组合梁的设计计算中通常忽略钢与混凝土界面上的黏结和摩擦作用，并将其作为一种安全储备，只考虑二者间的连接件作用[4-5]，这种方法对保证组合梁连接件的受力是安全的.然而，组合结构界面连接效应的研究对于全面理解剪力连接件的受力行为分析以及优化剪力连接件设计等具有实际意义.此外，随着组合结构桥梁技术的发展，一些新型的组合结构形式和施工方法开始在工程中应用[6]，如为了增强预应力的张拉效率而减少预应力施加到钢梁上，需要在混凝土桥面板中施加预应力使得混凝土与钢梁之间产生滑动，这时需要计算分析施工过程中克服钢与混凝土之间的黏结和摩擦需要施加的作用力的大小，目前，还未见有关计算分析组合梁中钢与混凝土之间黏结与摩擦效应的方法.随着数值计算方法的进步，一些新的计算技术和新型单元开发，使详细计算分析组合梁钢与混凝土界面上的连接效应也变成可能[7].本文结合通用有限元程序，提出一种能够模拟组合梁中钢与混凝土界面上黏结效应、摩擦效应及连接件传力的组合梁计算分析模型，并通过试验结果分析所提的计算模型的可行性.结合一组合梁具体工程计算分析不同界面连接效应下组合梁的受力及钢与混凝土界面滑移，计算组合梁中钢与混凝土界面黏接作用对连接件受力的影响.

1 组合梁结构受力模型的模拟

1.1 钢与混凝土界面连接效应的模拟

1.1.1 连接件的模拟

组合梁中的剪力连接件形式有很多种，其中焊钉连接件在传递剪力上没有方向限制，是目前组合结构中应用最广的一种连接件[8].在ANSYS程序中，钢与混凝土界面的焊钉连接件常采用弹簧单元Combin14模拟，弹簧单元有明确的方向性，一维单元只能模拟一个方向的受力，为了模拟出真实受力情况，在一对节点之间生成3个弹簧单元，分别代表焊钉连接件3个方向的受力性能，如图1所示，图中Kx，Ky，Kz分别为一个焊钉在x，y，z方向上的抗剪刚度.由于钢与混凝土界面上混凝土节点和钢梁节点位置重合，因此3个弹簧单元长度为零，每个弹簧单元的2个节点分别对应混凝土节点和钢梁节点[9].

图1 模拟焊钉连接件的三维弹簧模型Fig.1 3D spring element simulate stud connector

1.1.2 钢与混凝土界面黏结及滑移效应的模拟

国内外研究表明，钢与混凝土之间的黏结作用与光圆钢筋和混凝土之间的黏结相类似，主要由三部分组成[10-11]：①混凝土中水泥胶体与钢表面的化学胶结力；②钢与混凝土接触面上的摩擦力；③钢表面粗糙不平的机械咬合力.

在滑动之前，钢与混凝土之间的黏结作用主要取决于化学胶结力，胶结力是水泥浆体产生于2种材料界面上的化学吸附力.胶结力只在界面处于原始状态时才存在，一旦界面发生相对滑移，晶体被剪断、挤碎，胶结力就消失.在钢与混凝土之间产生滑动而胶结力丧失之后，起主要作用的是摩擦力和与钢表面粗糙度有关的咬合力.摩擦力取决于垂直于摩擦面的正应力和摩擦系数，因而与界面的粗糙程度有关，界面正压力直接来源于组合梁混凝土顶板对钢梁上翼缘板的压力.

对于有限元模拟组合梁中钢与混凝土界面黏结和滑移作用，目前常用的是接触单元.接触单元可以较好模拟静摩擦力和动摩擦力，并且能够考虑不同法向力对黏结强度的影响.同时，在后处理中接触单元可以提取滑移值、摩擦力、法向力等多种结果，便于数据的收集和整理.

ANSYS程序中提供了适合不同结构维度的多种接触单元类型，包括点-点接触分析、点-面接触分析和面-面接触分析.对于三维建模的组合梁模型常用的是3D面-面接触的TARGE170和CONTA173单元，如图2所示.一般地，处于接触状态的表面具有不互相穿透、能够传递法向压力和切向摩擦力、不传递法向拉力的特点.接触单元采用基本的库仑摩擦模型(图3)，库仑摩擦模型定义了一个等效剪应力τ，在某一法向压应力p作用下剪应力达到此值时表面开始滑动(τ=μp+τ0，其中μ是摩擦系数，作为材料特性定义，而τ0是黏聚力).一旦剪应力超过此值后，2个表面之间开始相对滑动.为了指定接触界面上最大容许剪应力，设置常数τmax，该常数用于修正在接触压力非常大时用库仑理论计算出的界面剪应力超过了材料的屈服极限的情况[12].

图2 模拟界面黏结的三维接触单元模型Fig.2 3D contact element simulate interface bonding

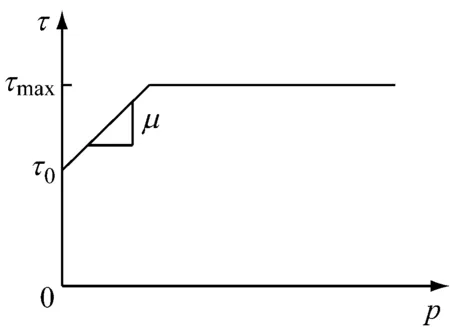
图3 摩擦模型Fig.3 Friction mode

根据试算结果，接触单元在模拟界面产生滑移状态后，除计入摩擦力作用，还计入了界面初始黏结力的作用.而实际情况是，在产生滑移后界面初始黏结力失效，即接触单元切向抗剪强度符合下述公式：

(1)

因此，接触单元不能直接应用于模拟组合结构界面连接效应，需要进行修正.本文通过对产生滑移接触单元的单元实常数进行修正的方法，并经过多次循环计算，即每次计算前将上次计算结果中产生滑移单元的实常数进行修正，使这些单元界面初始黏结力失效，弥补接触单元在不同状态下界面剪力分析中的不足.

1.2 混凝土与钢构件的模拟

混凝土为一种非均质材料，影响其力学特性的因素很多.在大型有限元软件ANSYS中，Solid65单元为三维八节点体单元，常被用来模拟钢筋混凝土和岩石等抗压能力远大于抗拉能力的非均质材料.本文采用Solid65六面体单元模拟组合梁中的混凝土结构.

Shell63是四节点的壳单元，既具有弯曲能力，又具有膜力，可以承受平面内荷载和法向荷载.本文采用Shell63单元模拟组合梁中的钢结构.

2 计算模型的验证

为验证用弹簧单元和接触单元模拟钢与混凝土界面连接效应的正确性，以Chapman等[13]的试验为算例.Chapman等于1964年成功进行了钢-混凝土简支组合梁的试验，由于其试验数据资料完整、结果可靠，经常被后来的研究者用来进行对比分析.

Chapman等所试验的简支组合梁结构形式如图4所示，梁长6 050 mm，混凝土翼缘宽1 220 mm.试验梁焊钉数量为100个，焊钉直径为13 mm、高50 mm，焊钉布置间距为120 mm.

Chapman等对试验梁均加载至破坏，因而在有限元模型中可进行弹塑性分析.模型中钢材的弹性模量Es=2.05×105MPa，屈服应力σy0=249 MPa，泊松比γa=0.3.混凝土的弹性模量Ec=2.67×103MPa，抗压强度fcu=50 MPa，抗拉强度ftu=5 MPa，混凝土采用Von Mises屈服准则，材料应力-应变关系采用下列表达式：

(2)

式中：σ为应力;ε为应变;Escnt为割线模量，并由最大压应力σc和对应的应变εc得出，Escnt=σc/εc，σc取圆柱体抗压强度值.

在有限元模型中，焊钉连接件用非线性弹簧单元剪切刚度模拟，按实际试验中的荷载-滑移曲线取，轴向刚度根据焊钉的尺寸计算.钢与混凝土界面黏结作用用3D接触单元模拟，对于钢与混凝土界面的黏结，试验中没有提及，根据相关文献取值，钢与混凝土界面在无压力情况下抗剪黏结强度(即接触单元的黏聚力COHE)取0.3 MPa，摩擦系数取0.7，其他参数采用ANSYS程序中的默认设置.根据上述尺寸以及材料特征建立有限元模型如图5所示.

a 半个试件

b 横断面图4 Chapman简支梁布置(单位：mm)

Fig.4 Schematic diagram of Chapman’s specimen(unit：mm)

图5 Chapman试验梁有限元模型Fig.5 FEA model of Chapman’s specimen

为更加清楚地分析用接触单元模拟钢与混凝土界面黏结的正确与否，在进行有限元计算时考虑2种情况分别计算，一种为钢与混凝土之间仅靠以弹簧单元模拟的焊钉连接件连接(ANSYS无黏结)，另一种为钢与混凝土之间除建立弹簧单元模拟焊钉连接件外，还建立接触单元模拟钢与混凝土之间的自然黏结(ANSYS有黏结).

图6为试验梁荷载随跨中挠度变化的试验结果和有限元计算结果，从结果可以看出有限元结果与试验结果比较吻合，说明本文采用的有限元模型是可靠的，从图中也可以看出，考虑接触单元与否对试验梁跨中挠度影响很小.

图6 试验梁荷载-跨中挠度曲线Fig.6 Load-deflection curve of specimens

图7为跨中集中荷载为440 kN时钢与混凝土之间滑移值沿跨径的分布，此时跨中钢梁下翼缘已经屈服，界面滑移主要集中在跨中附近，从结果可以看出有限元结果与试验结果比较吻合，且考虑接触单元的ANSYS有黏结结果更接近试验值，图8荷载-端部滑移曲线也验证了这一点.图8中ANSYS有黏结在荷载达到约300 kN时试验梁端部才开始滑移，而ANSYS无黏结在荷载较小时端部就存在滑移，因此，考虑接触单元的ANSYS有黏结结果更接近Chapman等的试验值.

图7 440 kN时试验梁界面滑移分布Fig.7 Interface slip distribution of specimens at 440 kN

图8 试验梁荷载-端部滑移曲线Fig.8 Load and end slip curve of specimens

根据上述分析，有限元结果与试验结果比较吻合，采用接触单元考虑钢与混凝土之间的黏结作用是可行的.

3 界面连接效应对组合梁受力的影响

3.1 工程背景介绍

工程采用某两跨各为50 m的连续槽形钢箱组合梁桥，组合梁横断面如图9所示，混凝土顶板宽12.75 m，平均厚度300 mm，腹板处加厚至550 mm，槽形钢梁高3 000 m，底板宽6 500 mm，上翼缘板宽1 000 mm，跨中处钢梁上翼缘板、腹板、底板厚度分别为30,20,26 mm，支座处钢梁上翼缘板、腹板、底板厚度分别为36,30,20 mm.中支座底板处采用内衬底板混凝土.施工方法采用一次落架.

a 跨中断面

b 中支点断面图9 横断面(单位：mm)Fig.9 Cross section(unit: mm)

焊钉连接件的直径为22 mm，高度为300 mm，焊钉在钢梁上翼缘板横桥向布置6排，间距为150 mm，纵桥向满布，间距为150 mm.布置形式如图10所示.焊钉切向刚度取400 kN·mm-1，轴向刚度取250 kN·mm-1.钢与混凝土界面黏结作用采用三维接触单元Conta173和Targe170模拟，取钢表面处理方式为采用环氧富锌底漆时的界面黏结强度和摩擦系数，即接触单元初始黏结强度COHE取0.3 MPa，摩擦系数取0.7，其他参数采用默认值.

计算内容主要为：①恒载，考虑一期恒载和二期恒载；②正常使用短期组合，考虑一期恒载、二期恒载、车道活载、整体降温、梯度降温、混凝土收缩作用以及支座沉降.荷载均按中支点负弯矩最不利情况布置.各主要材料参数和荷载如下.

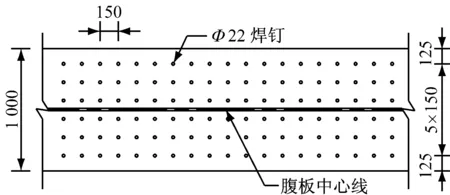
图10 焊钉布置示意(单位：mm)Fig.10 The arrangement of stud connectors(unit: mm)

(1)材料.钢材：Q345qC，密度78.5×10-6N·mm-3，弹性模量2.06×105MPa，线膨胀系数1.2×10-5℃-1，泊松比0.3.混凝土：C60，密度25×10-6N·mm-3，弹性模量3.45×104MPa，线膨胀系数10-5℃-1，泊松比0.2.

(2)一期恒载.为桥梁主体结构自重.

(3)二期恒载.桥面为100 mm沥青混凝土铺装(重度取24 kN·m-3)；每侧栏杆每延米重量为10 kN.

(5)整体降温.考虑结构整体温度变化，整体降温27 ℃.

(6)梯度降温.考虑结构梯度温度变化，仅把混凝土温度降低7 ℃，其余部分温度保持不变.

(7)混凝土收缩作用.将混凝土降温15 ℃进行模拟.

(8)支座沉降.根据中支点负弯矩最不利情况，考虑边支座沉降16.67 mm、中间支座保持不变.

3.2 仅考虑黏结效应的组合梁受力

仅考虑黏结效应而不考虑剪力连接件效应，即钢与混凝土间仅靠接触单元连接，计算荷载分别为恒载和短期组合时的组合梁受力情况如表1所示.

表1 仅考虑黏结效应的组合梁受力情况Tab.1 The behavior of composite girder only considering interface bonding

注：a为中支点顶板混凝土纵桥向最大拉应力，b为中支点钢梁上翼缘板处最大Mises应力，c为界面滑移率，d为界面最大滑移值.

分析接触单元计算结果，在恒载和短期组合下全桥接触单元的接触状态如图11所示，图中虚线表示滑移方向向右，实线表示滑移方向向左.由图可见，在仅考虑黏结效应的情况下，在恒载情况下钢与混凝土界面几乎全部发生破坏和滑移，滑移面约占全部界面的98%，黏结面主要分布在靠近边支点18 m范围处的小块区域；在短期组合下钢与混凝土界面会全部发生破坏和滑移.

图11 界面黏结滑移状态(单位：m)Fig.11 Interface bonding condition(unit: m)

图11中的滑移方向指向混凝土顶板相对钢梁上翼缘板滑动方向，这里规定箭头向左的滑移值为正，得到恒载和短期组合下滑移值(提取位置为钢梁上翼缘板与腹板交界处，下同)分布形状如图12所示，图中横坐标为桥梁纵桥向位置，原点位于桥左端.由图可知两者形状基本一致，不同的是：在恒载下滑移值最大为3.52 mm，在短期组合下滑移值最大为7.69 mm；在短期组合下滑移值相对恒载时较大；在短期组合下因左跨跨中有车道荷载的集中荷载，两跨界面滑移值不对称，且左跨较大.在恒载下距边支座17 m处滑移方向发生改变，而在短期组合下距边支座13 m处滑移方向发生改变，界面滑移方向变化点向边支座移动了4 m.

图12 仅考虑黏结效应的界面滑移分布Fig.12 Interface slipping distribution only considering interface bonding

3.3 仅考虑连接件效应的组合梁受力

仅考虑连接件效应而不考虑黏结效应，即钢与混凝土间仅靠焊钉弹簧单元连接，计算荷载分别为恒载和短期组合时的组合梁受力情况如表2所示.

在恒载和短期组合下滑移分布曲线如图13所示，两者形状基本一致，纵向滑移绝对值最大均不超过0.1 mm.在短期组合下，滑移值略有增加，在恒载下最大滑移绝对值约为0.07 mm，而在短期组合下最大滑移绝对值约为0.08 mm.对于考虑剪力连接件效应，组合梁钢与混凝土之间的连接刚度较大，所以界面滑移较小.

表2 仅考虑连接件效应的组合梁受力情况Tab.2 The behavior of composite girder only considering connectors

图13 仅考虑连接件的界面滑移分布Fig.13 Interface slipping distribution only considering connectors

提取在恒载和短期组合下焊钉剪力分布如图14所示，在恒载和短期组合下组合梁剪力钉的剪力分布形状基本一致，在恒载时焊钉最大剪力为26 kN，短期组合时最大剪力为30 kN，剪力最大值均出现在靠近中支座4 m左右处.

图14 仅考虑连接件的焊钉纵向剪力分布Fig.14 Longitudinal shear force distribution of stud connectors only considering connectors

3.4 考虑黏结效应和连接件效应的组合梁受力

考虑均布剪力钉和界面黏结作用，即钢与混凝土间既有焊钉弹簧单元连接又有接触单元连接，计算荷载为恒载和短期组合时的中支点处顶板混凝土及钢梁的应力结果如表3.表3还列出仅考虑黏结作用(情形A)和仅考虑剪力连接件作用(情形B)以及2种作用均考虑(情形C)的计算结果.

表3 不同连接件效应的组合梁受力情况

Tab.3 The behavior of composite girder with different connecting conditions

组合梁连接情形荷载形式a/MPab/MPac/%d/mmA恒载短期组合3．66．390170981003．527．69B恒载短期组合7．311．840900．070．08C恒载短期组合7．311．840900．070．08

对比连接情形B和C可得，在考虑剪力连接件时，无论在恒载还是短期组合下，是否考虑界面黏结作用对组合梁混凝土顶板和钢梁的应力以及界面滑移的影响都很小.然而对比连接情形A和C可得，在考虑界面黏结作用时，无论在恒载还是在短期组合下，是否考虑剪力连接件对组合梁混凝土顶板和钢梁的应力以及界面滑移的影响都较大.考虑剪力连接件后，中支点混凝土最大拉应力增加1倍左右，而中支点钢梁上翼缘板最大Mises应力减小约1/2.连接件的有无对界面滑移产生完全不同的影响，当有连接件时界面基本无滑移，而无连接件时界面基本上全部滑移.由上述分析可得，在正常使用情况下，影响组合梁的钢梁和混凝土受力以及界面滑移的主要因素为剪力连接件，是否考虑界面黏结作用对组合梁的钢梁和混凝土受力以及界面滑移影响很小，可以忽略.

在不同荷载下考虑界面黏结和不考虑界面黏结的焊钉剪力分布如图15所示，由对比分析可得，考虑界面黏结作用会分担一部分剪力连接件的剪力，使焊钉的剪力在恒载下平均约减少25%，在短期组合下平均约减少20%.说明若考虑焊钉连接件作用，在恒载和活载作用时，钢与混凝土界面黏结作用也分担剪力，是钢-混凝土组合梁剪力受力行为不可忽略的一部分.在短期组合时，界面黏结作用对焊钉帮助减小，分析可能的原因是，在短期组合下，部分界面开始滑移，界面黏结作用对界面剪力的承担减小.

4 结论

利用有限元程序ANSYS对组合梁钢与混凝土界面连接效应进行模拟，得到了以下结论：

(1)在ANSYS程序模拟组合梁受力时，采用弹簧单元模拟焊钉连接件、接触单元模拟钢与混凝土之间的黏结作用，能够有效模拟组合梁钢与混凝土的各种连接作用.

a 恒载

b 短期效应组合图15 考虑2种效应的焊钉纵向剪力分布

Fig.15 Longitudinal shear force distribution of stud connectors considering interface bonding and connectors

(2)在正常使用的情况下，影响组合梁的钢梁和混凝土受力以及界面滑移的主要因素为剪力连接件，相比不考虑剪力连接件，考虑剪力连接件时中支点混凝土最大拉应力增加1倍左右，而中支点钢梁上翼缘板最大Mises应力减小约1/2，界面滑移率也由无连接件的基本全部滑移变为考虑连接件的基本无滑移，是否考虑界面黏结作用对组合梁的钢梁和混凝土受力以及界面滑移影响很小，可以忽略.

(3)考虑界面黏结作用会分担一部分剪力连接件的剪力，使焊钉的剪力在恒载下平均减少约25%，在短期组合下平均减少约20%.考虑焊钉连接件作用，不论恒载还是短期组合时，钢与混凝土界面黏结作用也分担剪力，是钢-混凝土组合梁剪力受力行为不可忽略的一部分.

[1] 黄侨.桥梁钢-混凝土组合结构设计原理[M].北京:人民交通出版社,2003.

HUANG Qiao. Bridge steel-concrete composite structure design principle[M].Beijing: China Communication Press,2003.

[2] Roeder C W. Composite and mixed construction[M]. New York: American Society of Civil Engineers, 1985.

[3] 李红.型钢与混凝土黏结性能的试验研究[D].西安:西安建筑科技大学, 1995.

LI Hong. The experimental study of bond behavior between steel and concrete[D]. Xi’an: Xi’an University of Architecture and Technology, 1995.

[4] CEN-European Committee for Standardisation. BS EN 1994-2 Eurocode 4: Design of composite steel and concrete structures, Part 1-1: General rules and rules for buildings[S]. Brussels: CEN-European Committee for Standardisation, 2004.

[5] 日本道路协会.道路桥示方书同解说——Ⅱ钢桥篇[S]. 东京:日本土木学会，2002.

Japan Road Association. Specifications for highway bridge-part Ⅱ:Steel bridge[S]. Tokyo:Japan Society of Civil Engineers, 2002.

[6] 苏庆田，杨国涛，吴冲.预制预应力混凝土板组合梁受力性能试验[J].同济大学学报:自然科学版，2012,40(7):996.

SU Qingtian, YANG Guotao, WU Chong. Experimental studies on mechanical behavior of continuous composite girder with prefabricate prestressed concrete slab[J].Journal of Tongji University:Natural Science, 2012,40(7): 996.

[7] 王新敏. ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.

WANG Xinmin. ANSYS numerical analysis for engineering structures[M].Beijing:China Communications Press, 2007.

[8] 刘玉擎.组合结构桥梁[M].北京:人民交通出版社,2005.

LIU Yuqing. Steel-concrete hybrid bridge[M].Beijing: China Communications Press,2005.

[9] 苏庆田,郭淑卿.组合梁结合面连接的力学性能研究[C]∥第17届全国结构工程学术会议论文集.武汉:华中科技大学,2008:512-517.

SU Qingtian, GUO Shuqing. Mechanical behavior of connected action in the interface of composite beam[C]∥Proceedings of the 17th National Conference on Structural Engineering.Wuhan: Huazhong University of Science and Technology,2008:512-517.

[10] 李红,安建利,姜维山.型钢与混凝土黏结性能的试验研究[J].哈尔滨建筑工程学院学报, 1993(S1):214.

LI Hong, AN Jianli, JIANG Weishan. An experimental investigation on bond behavior between steel and concrete[J].Journal of Harbin University of Civil Engineering and Architecture, 1993(S1):214.

[11] 郑山锁,杨勇,薛建阳,等.型钢混凝土黏结滑移性能研究[J].土木工程学报, 2002, 35(4):47.

ZHENG Shansuo, YANG Yong, XUE Jianyang,etal. Study on bond slip behavior between section steel and concrete in SRC structures[J]. China Civil Engineering Journal, 2002,35(4):47.

[12] 王新敏,李义强,许宏伟.ANSYS结构分析单元与应用[M].北京:人民交通出版社,2011.

WANG Xinmin, LI Yiqiang, XU Hongwei. ANSYS structural analysis element and application[M].Beijing: China Communications Press, 2011.

[13] Chapman J C, Balakrishnan S. Experiments on composite beam[J]. The Structural Engineer ,1964:42(11):369.

Refined Calculation of Steel-concrete Interface Connection in Composite Girders

SUQingtian1，XUEZhibo1，LIChenxiang2，JIANGXu1

(1. College of Civil Engineering， Tongji University， Shanghai 200092， China； 2. Shanghai Municipal Transportation Design & Research Institute Co. Ltd.， Shanghai 200030， China)

In order to quantitatively reveal the combination of steel and concrete interface, an analysis method was provided for the calculation of composite girder considering connectors, bond stress and friction in the interface between the steel and the concrete. The feasibility of the method was also verified through the experiment. This method was used to analyze the relationship between different steel-concrete connecting conditions and interface slip and also the effect of the present or not of the interface bonding on the mechanical behavior of the composite girder was analyzed. The results show that, the steel-concrete interface bonding effect has a tine effect on the stress of the concrete slab and steel girder, but has a large effect on the shear force of the connectors where the maximum effect can reach 25 percent under different loads.

composite girder； analysis method； bond stress； connector； nonlinear finite element method

2016-03-16

国家“九七三”重点基础研究发展计划(2013CB036303)；国家自然科学基金(51408424)

苏庆田(1974—)，男，教授，博士生导师，工学博士，主要研究方向为钢桥及组合桥梁.E-mail：sqt@tongji.edu.cn

姜 旭(1982—)，男，讲师，硕士生导师，工学博士，主要研究方向为钢桥及组合桥梁.E-mail：jiangxu@tongji.edu.cn

TU312

A