无规矩不成方圆——以三视图为例谈立体几何中的还原策略

☉湖南省长沙市麓山国际实验学校 刘玲珑

无规矩不成方圆
——以三视图为例谈立体几何中的还原策略

☉湖南省长沙市麓山国际实验学校 刘玲珑

三视图是高考对立体几何模块的常考题型，考查角度主要有：由三视图求几何的棱长、面积、体积；给出几何体判断其三视图等.本文将对此类问题的求解策略归纳总结.以期对学生解答此类问题有所帮助.

一、明确命题根源

从命题的角度来看，此类试题通常以学生所熟悉的常规几何体为背景，如长方体、正方体等，将长方体或正方体经过切割、分解以后，以新的面目呈现在我们面前.如图1所示的正四面体，就可以理解为将正方体切割掉4个角后所得的几何体.

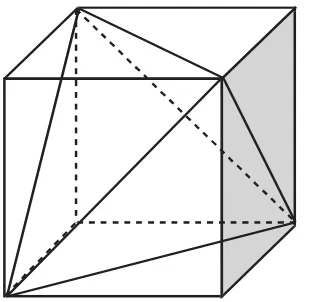
图1

因此在解答相关问题时，我们可采用还原策略，即将所考查的几何体还原在常规几何体中，从而寻找问题的简洁解法.

例1已知三条侧棱两两垂直的正三棱锥的俯视图如图2所示，那么此三棱锥的体积是_________，左视图的面积是_____________.

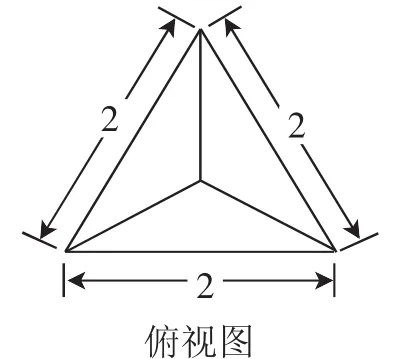
图2

解法1：（常规解答）设三棱锥为S-ABC（如图3所示），CD为三角形ABC的中线，作三棱锥的高SM，易知点M在CD上，且点M为三角形ABC的重心.

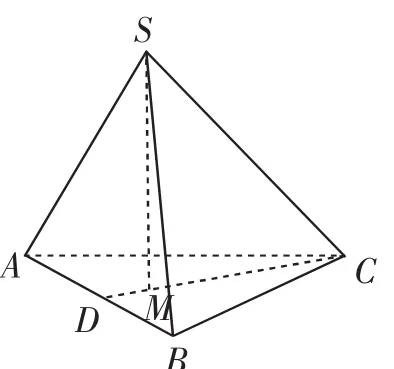
图3

因为三角形ABC为等边三角形且边长为2，所以三角形ABC的高，其面积为

解法2：（还原策略）根据题目条件可知该三棱锥为正方体的一个角，如图4所示.所以

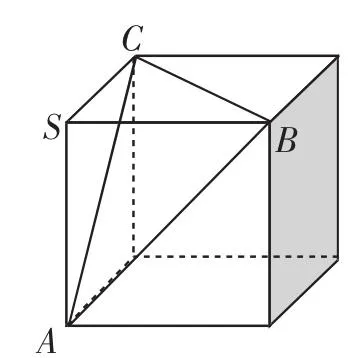
图4

评注：通过以上两种解法的对比，其优劣程度一目了然.因此在处理相关问题时要准确把握几何体的特征，准确还原.

二、还原特殊几何体

1.还原于正方体

例2某三棱锥的正视图如图5所示，则这个三棱锥的俯视图不可能是图6中的（ ）.

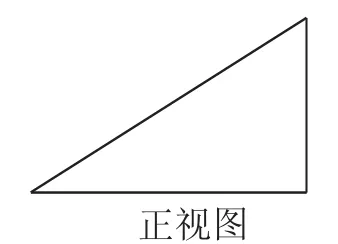
图5

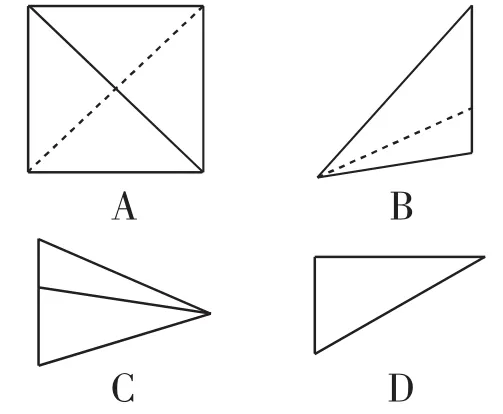
图6

解析：对于选项A，可还原几何体，如图7所示.

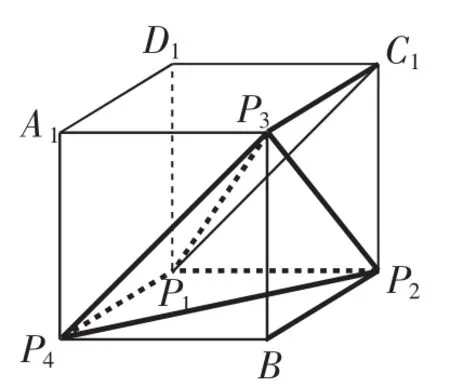
图7

对于选项B，可还原几何体，如图8所示.

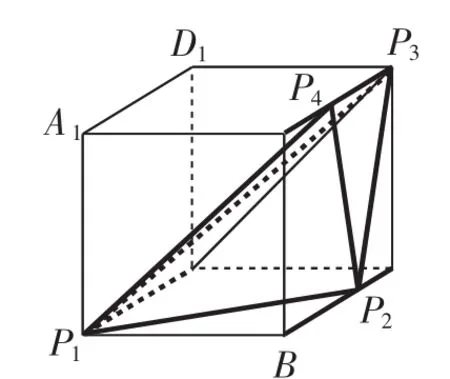
图8

对于选项D，可还原几何体，如图9所示.

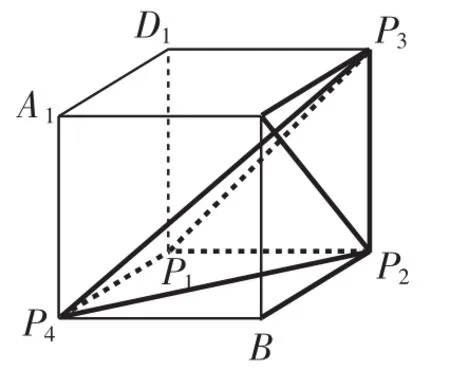
图9

故正确选项为C.

评注：不考算，只考想！重点考查空间想象能力、逻辑推理能力.在处理类似问题时不能仅仅停留在直觉层面.拓展思考：（1）俯视图不确定，能否对所有可能情形进行分类？（2）如果再给出左视图，能否确定俯视图呢？

例3 如图10，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中最长的棱的长度为（ ）.

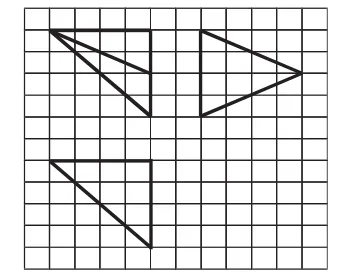
图10

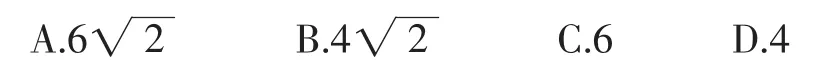
解析：如图11所示，原几何体为三棱锥D-ABC，其中AB=BC=4，AC=4，DB=DC=2，DA=故最长的棱的长度为DA=6，选C.

图11

评注：在正方体中找到三棱锥各顶点所在位置是准确还原几何体的关键所在.

2.还原于长方体

例4某三棱锥的三视图如图12所示，则该三棱锥的表面积是（ ）.

图12

解析：该几何体的长、宽和高不相等，故可将其还原于长方体中，如图13所示.由三视图可知长方体的长、宽、高分别为5、4、4，所以在三角形SAB中，利用勾股定理求得所以三角形SAB是以SA为底边的等腰三角形，易求得其高为6，所以所以该三棱锥的表面积为故正确选项为B.

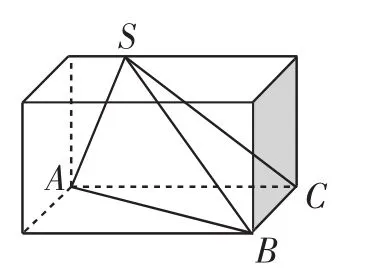
图13

评注：将所求三棱锥还原于长方体中，利用长方体的有关性质将问题直接求解.

例5某三棱锥的三视图如图14所示，则该三棱锥四个面中面积最大的是（ ）.

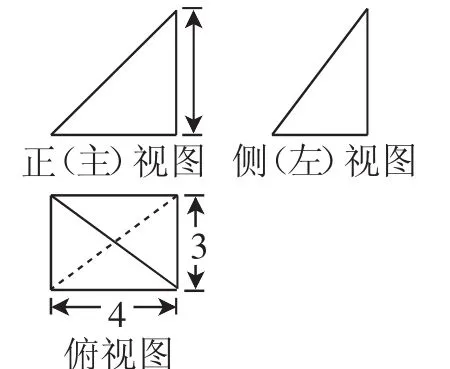
图14

解析：由三视图可将该三棱锥还原到长方体中，如图15所示，三棱锥C′-ABD即为已知三棱锥.结合长方体的几何特征易求得在三角形C′AD中，C′A=所以故正确选项为A.

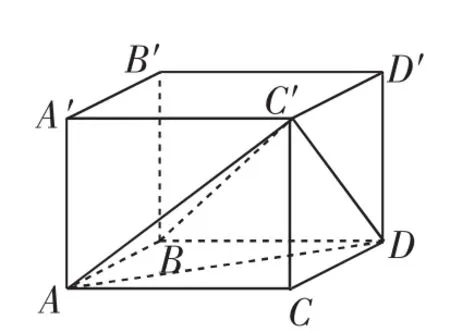
图15

评注：在三视图问题的解答中要注意实线与虚线的区别.本题条件为三棱锥，但俯视图为四边形，故其中一点为顶点的投影，进而准确还原.

总之，用好还原策略是解答三视图问题的有效策略.在解答问题时要准确把握所求几何的相关特征、准确还原.