基于CDIO的概率统计实验研究

沈小芳

（武昌首义学院，湖北 武汉 430064）

基于CDIO的概率统计实验研究

沈小芳

（武昌首义学院，湖北 武汉 430064）

基于CDIO模式，从实验内容的改进、形式的转变两个方面对概率统计的实验进行了研究和探讨，以提高概率统计的工程应用能力，特别是概率统计知识的运用能力、实践动手能力和解决实际问题的建模能力。

CDIO；概率统计；Matlab；数学实验

CDIO是构思（Conceive）、设计（Design）、实施（Implement）、与运行（Operate）的缩写，此教育模式是麻省理工学院、瑞典皇家工学院等大学经过多年探索形成的国际工程教育改革的最新成果。CDIO旨在培养学生综合应用能力，将学科导向改变为项目导向，将应试教育转变为应用能力教育，变强调知识的严谨性为注重项目训练的完整性［1］。笔者在CDIO工程教育模式的指导下，结合概率统计自身的特点，从教学内容、教学形式2个方面对《概率论与数理统计》的课堂教学进行了研究和探讨。

1 教学内容的改进

1.1 精选多样化例题，开展课堂讨论

CDIO教育模式强调培养学生的学习兴趣，学习兴趣的加强无疑会激发学生学习的动力，而学习的动力则是学生进行主动学习的内驱力。在概率统计里趣味性的例子比比皆是，精选贴近现实生活的例题，以激发学生的学习兴趣，让学生在解决具体问题的过程中具有成就感。最后教师可以对学生讨论进行总结，给以合理的解答。比如在讲授“古典概型”加法公式时，引入下面这个例子。

问题提出：“三个臭皮匠，顶个诸葛亮。”请通过概率原理加以论证。

问题假设：假设诸葛亮解决问题的概率为0.8，3个臭屁匠独立解决问题的概率为

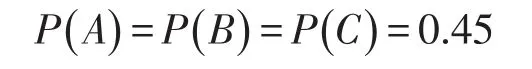
且每个人解决问题是相互独立的。

问题求解：3个臭皮匠至少有1个能解决问题的概率可由加法公式求解：

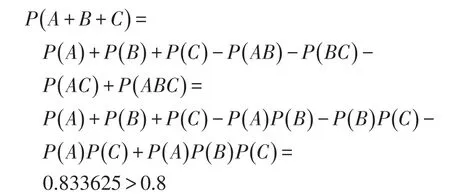
即3个聪明的臭皮匠解决问题的可能性超过了80%，和诸葛亮解决问题的概率差不多。

学生通过思考解决问题的过程，加深对加法定理的理解，由于研究的问题耳熟能详，研究背景朴素，对学生的认知触动也是非常显著的。

1.2 开展案例教学，培养建模能力

CDIO教育模式注重学生的工程建模能力的培养。《概率论与数理统计》是从实际生产中产生的一门应用性学科，它来源于实际又服务于实际。因此，采取案例教学法，重视理论联系实际，可以使教学过程充满活力，学生在课堂上能接触到大量的实际问题，可以提高学生综合分析和解决实际问题的能力。比如在讲授二项分布时，为了加深学生对知识的理解，以“盥洗室问题”为实例。

问题提出：宿舍楼的盥洗室在用水高峰时，老是需要排队等待，学生意见很大。学校领导把他作为一道数学问题，希望学生从理论上，给出一个合理的解决方案。

问题分析：引导学生调查研究收集资料，宿舍楼有500名学生，盥洗室有50个水龙头，用水高峰约2 h（120 min），每名学生用水时间平均12 min，等待时间不长（最多12 min），但经常等待实在恼人，同学们的要求合情合理，希望100次用水中，需要等待的次数不超过5～10次。

问题假设：1）楼上（下）的学生可以到楼下（上）用水，不必再按楼层调查人数。500名学生随机地用这50个龙头。2）同学们的要求是概率值，因此归结为概率问题。从条件中找概率：一名学生在盥洗室（用水）的概率为0.1（12/120）。3）增加水龙头是最简单最实际的解决办法，安装多少个水龙头才能既能缓解学生的用水紧张，又不造成浪费。

问题求解：出现在盥洗室的学生超过50人就要等待，学生数是变化的，而且是随机的，最好的办法是用随机变量来描述。

第1步数学化：设X是某时刻用水的学生数，利用所学的知识，独立的500人，单个用水的概率是0.1，现在是X人用水，类似于独立实验序列，因此用二项分布比较适合，故设X服从二项分布，n为500，P为0.1。

第2步计算：关心不需要等待（X<50）的概率：

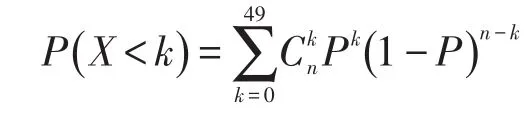
这是一个初步的模型，是一个二项分布问题，可以按二项分布来计算。由于n很大（n=500），直接用二项分布计算太复杂，因此利用二项分布的2种简化近似公式（泊松分布和正态分布）来计算：

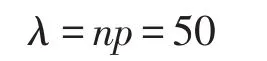
λ值太大，利用泊松分布来近似计算并不理想。因而考虑用正态分布来近似会更方便，计算得

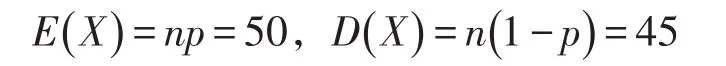
所以用X～N（50，45）来近似计算。即所要的结果为P（X<50）为0.5，说明学生等待的概率为0.5，相当于每2次用水就有1次等待，数据很有说服力。

第3步改进方案：如果将水龙头增加到x个，则等待概率为

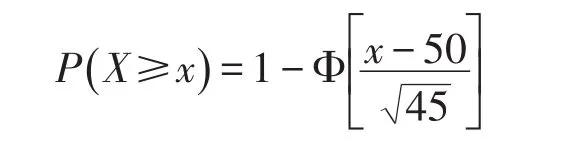
学生们希望这个概率是0.05～0.1，即当P为0.05时，查正态分布表得到x为61.28；当P为0.1时，查正态分布表得到x为58.6，说明水龙头的个数在59～62个时学生等待的概率比较合理。

通过此问题的解决，让学生体会到了自己动手收集、分析数据、建立模型、解决实际问题的乐趣，让学生经历较系统的数据处理全过程，在此过程中学习一些数据处理的方法，并运用所学知识和方法去解决实际问题，提高了学生应用数学的能力。

2 教学形式的转变

2.1 采用多媒体教学

多媒体教学与传统的教学法相比有着不可比拟的优势。一方面，由于概率统计例题字数较多，抄题很费时间。制作多媒体课件，教师有更多的精力对内容进行详细地分析和讲解，增加与学生的互动，增加课堂信息量。比如在概率部分，把几个重要的离散型随机变量、连续型随机变量的分布率、概率密度、期望、方差等列成表格；在统计部分，将正态总体均值和方差的置信区间，假设检验问题的拒绝域列成表格形式，其中所涉及到的重要统计量的分布密度函数用图形表示出来，通过让学生先了解图形的特点，再结合分位数的有关知识，找出其中的规律，理解其含义及联系，加深了学生对概念的理解及方法的运用，以便更容易记住和求出置信区间和假设检验问题的拒绝域。对于教材中的重点、难点、复习课、习题课等都制作成多媒体课件形式，配以适当的黑板演算教学，这样既能延续一贯的听课方式，发挥教师的主导作用，又能充分体现学生的认知主体作用。另一方面，多媒体教学适时用Matlab生动形象的演示，可将一些抽象内容直观地反映出来，使学生更容易理解。比如在讲授概率的概念时，会讲到“频率是概率的近似值”，“概率是频率的极限值”，引入Matlab程序，模拟抛硬币试验，经过不同次数抛硬币看频率的数值波动变化，通过图像结果让学生深刻理解这一概念。Mat⁃lab程序设计如下：

程序的运行结果如图1所示。

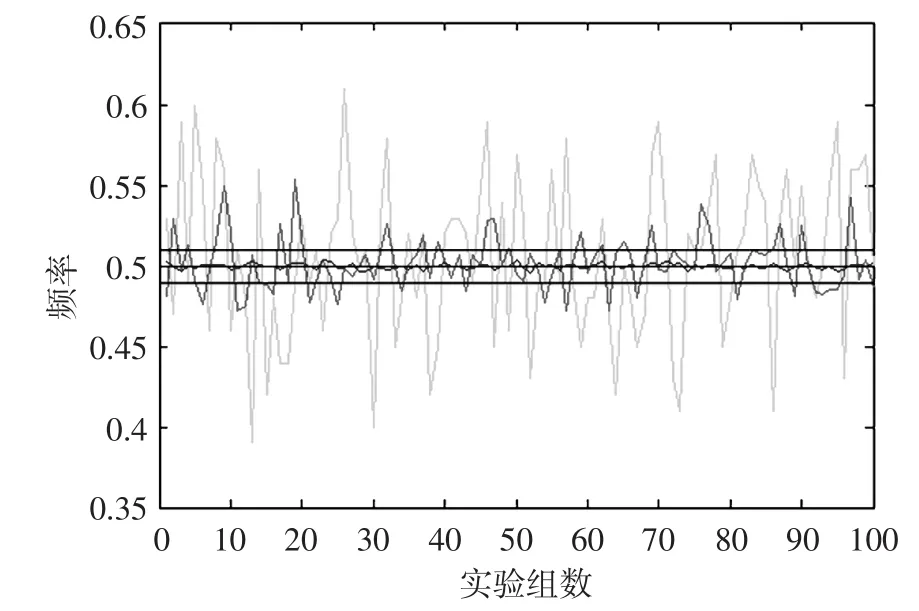
图1 抛硬币试验频率与概率偏离图

又如在学习二维正态分布时，对于二维正态分布的密度函数曲面图像，如果只靠板书和口头讲解是很难了解到其空间形状，通过Matlab软件编写如下程序：

得到如图2所示立体图形，二维正态分布的密度函数曲面图像完美直观展示，这样学生对相关参数的作用有了直观的印象，加深学生对于公式的理解，激发学生的空间想象思维。

2.2 开设数学实验课

CDIO教育模式主张用问题启发学生思维，让学生在实践中去发现问题解决问题，从中获得经验和技能。数学实验主要是以计算机数学软件的应用为平台，结合数学模型，模拟实验环境进行的教学模式，可以使用这些软件来解决有较大数据量和较强应用性的概率或统计方面的案例。

实验案例1：中心极限定理的验证实验

中心极限定理［2］指的是N个独立同分布的随机变量的和分布近似服从正态分布，设计随机模拟实验来验证中心极限定理。Matlab程序如下：

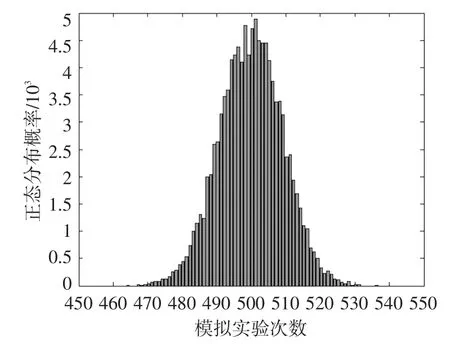
图3 中心极限定理验证试验结果

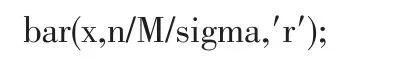
通过实验得到图3，通过实验学生更深的认识到中心极限定理的理论意义及其应用价值。

实验案例2：线性回归分析

为了测定刀具的磨损程度随时间t的变化，每隔1 h一次刀具的厚度，得到数据如表1所示。

Matlab程序如下：

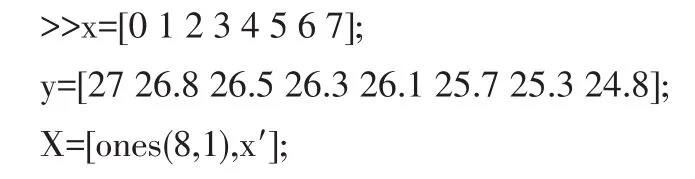
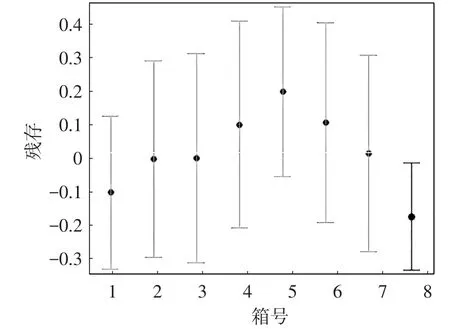
图4 残差分析图

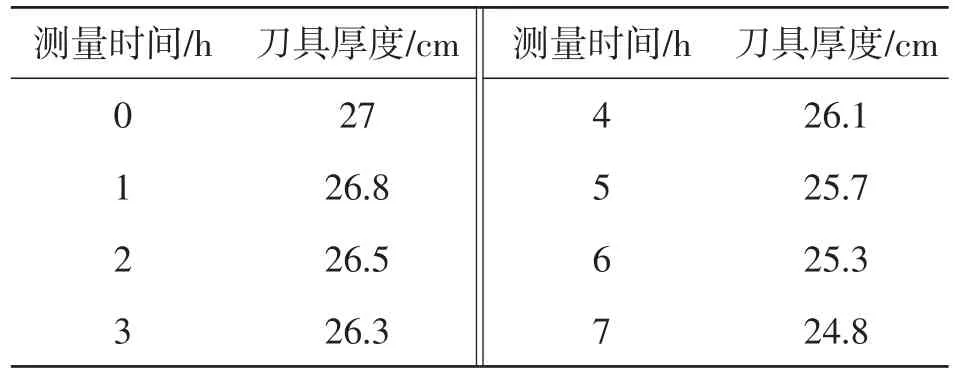
表1 刀具厚度与时间关系

残存分析图和回归直线图如图4～5所示，通过概率统计实验不仅让学生体会到应用概率统计知识进行数学建模的全过程，而且学生通过软件的学习应用，进一步增强了数学理论应用意识，这样既丰富了学生的实践活动，又增强了学生的实践动手能力和解决实际问题的能力。

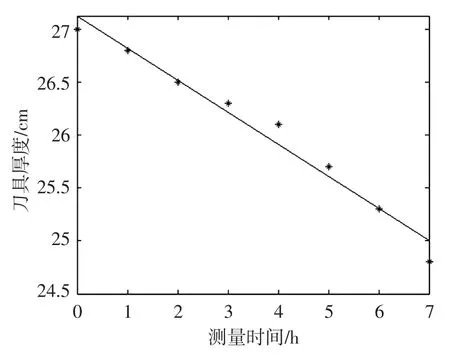
图5 散点图与回归直线图

3 结束语

概率统计教学要想在培养学生实践能力和创新能力方面有所突破，必须打破单一的讲授式教学形式，探索和尝试新的教育模式，CDIO工程教育模式无疑是一个有益的尝试。基于CDIO工程教育模式，概率统计教学在教学内容上要从学生角度出发组织教学内容，与时代发展接轨适时更新教学内容，抓住学生的兴趣点，启发学生的创新思维，同时培养学生的建模能力；在教学形式上应该采用丰富的教学手段，充分调动学生的思维积极性，激发学生的学习热情，培养其创新和实践能力。

［1］Crawley E.重新认识工程教育——国际CDIO培养模式与方法［M］.顾佩华，沈民奋，陆小华，译.北京：高等教育出版社，2009：1-11.

［2］盛骤，谢式千，潘承毅.概率论与数理统计［M］.4版.北京：高等教育出版社，2008：145.

［3］郑喜英，孔波.基于Matlab的概率统计教学研究［J］.河南教育学院学报（自然科学版），2014，23（1）：56-59.

［4］张冬梅，王幸刚，高雪芬.在概率统计教学中引导学生进行研究性学习的若干措施［J］.教学研究，2015（2）：17-20+26.

Research on Experiment of Probability Statistics Based on CDIO

Shen Xiaofang
（Wuchang Shouyi University,Wuhan430064,China）

Based on CDIO,the experiment methods were investigated from the two aspects of the experi⁃mental content and the experiment pattern for the probability statistics in order to improve the engineer⁃ing application ability of probability statistics,especially the professional knowledge application ability, hands-on practical ability,and modeling ability for practical problem-solving.

CDIO;probability statistics;Matlab;mathematics experiment

O211

：A

：1008-5483（2016）04-0077-04

10.3969/j.issn.1008-5483.2016.04.018

2016-04-07

沈小芳（1979-），女，湖北随州人，硕士，从事概率与数理统计研究。E-mail:914077819@qq.com