基于极值理论的我国钢铁期货市场风险度量研究

陈迪芳

（湖北汽车工业学院 理学院，湖北 十堰 442002）

基于极值理论的我国钢铁期货市场风险度量研究

陈迪芳

（湖北汽车工业学院 理学院，湖北 十堰 442002）

以极值理论为模型基础，对比不同的计算模型，算出我国钢铁期货的风险值（VaR），研究结果表明：采用极值理论建立的模型能够较好地刻画收益率分布的尾部特征，优于传统的VaR模型。

极值理论；VaR；回归测试

1 模型的建立

由于极值方法对数据的尾部拟合一个极值分布函数，一旦知道尾部参数，就能扩张到样本外的分布，来考虑历史上尚未观察到的，但是可能出现的极值运动。正因为极值方法只考虑分布的尾部，因而能够精确地估计极端分位数。

BMM法：对整个时序数据进行分段，每段取最大值而组成的序列渐进地服从一个广义极值分布GEV，接着估计分布参数，从分布参数中求出相应置信度的分位数，最后计算VaR的值。

POT法：选定一个高的阈值，超过阈值的数据近似服从一个广义Pareto分布，然后对分布进行参数估计，计算VaR值。

由于VaR可以被定义为可能损失分布的第P分位数，一般选择P值等于0.05或0.01，即VaR=F-1(1-p)，分2种情况来分别进行讨论：

1）当F分布是广义极值分布（GEV），由广义极值分布（GEV）公式

计算分位数函数，即求这个函数的反函数，将VaR=F-1(1-p)代入，可求VaR得：

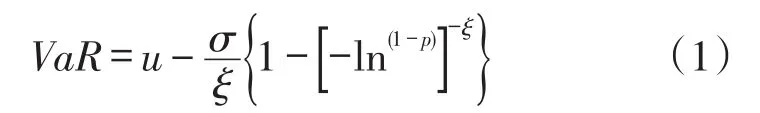
2）当F分布是广义Pareto分布（GPD），由Pare⁃to分布（GPD）的尾部估计公式求反函数分位数函数，再将VaR=F-1(1-p)代入，得出VaR，即

这里需要用阈值法来选取合理的阈值以及对参数u,σ,ξ的估计。

3）在传统对于VaR模型的研究中，最常用的方差-协方差法给定了资产收益率序列服从正态分布的理论假设前提，这个假设往往与金融资产所具有的“尖峰厚尾”的分布特征所不相符合。极值理论的引入，是考虑到小概率极端事件的发生所带来的损失对风险度量过程产生的影响，是为了弥补传统的VaR模型因缺乏对极端情况的关注而低估了尾部风险。因此，不仅关注金融数据序列的尾部风险而将极值理论引入，而且考虑序列的波动的集聚性情况，将TARCH模型与极值理论结合起来应用到VaR模型中，将有助于提高模型的精度。

TARCH-GPD-VaR模型的构建如下：首先对钢铁期货收益率序列进行TARCH族模型的估计，提取修正后的残差序列ε̂t，应用极值理论，对残差序列选取阈值并进行GPD分布拟合，得到残差的VaR值，记为VaRε，得TARCH-GPD-VaR模型的VaR计算表达式为

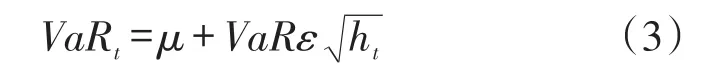
方差-协方差法的VaR模型与ARCH-VaR模型为

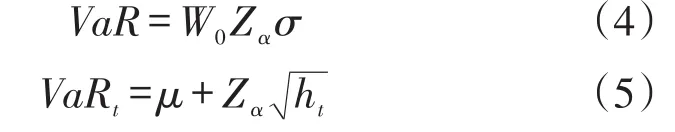
2 我国股市数据的实证分析

2.1 数据的选择与基本统计量描述

本文中选择上海期货交易所我国螺纹钢连续(RB0)期货日收盘价作为数据样本来进行实证研究，数据区间为2009年3月9日-2015年12月31日，扣除节假日共计1635个交易日。数据来源于WIND数据库。收益率计算公式为

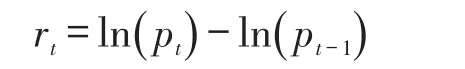
式中：pt和pt-1分别表示第t天和第( )t-1天交易日的收盘价。

利用软件对钢铁期货收益率序列进行描述性统计、JB检验，并作出收益率序列正态分布Q-Q图，所得结果如表1和图1所示。

表1 收益率序列描述性统计表

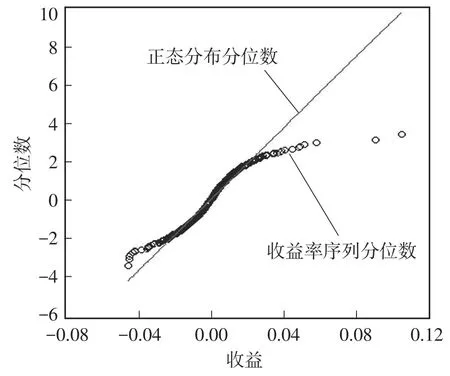
图1 收益率序列正态分布Q-Q图

从表1及图1可看出：钢铁期货收益率序列进偏度S=0.864 366>0，峰度K=12.608 85>3，JB统计量非常大，相应的概率为0，说明其具有“尖峰、厚尾”的特征，不服从正态分布。从图1可以看出：样本数据散点的中间一段与正态分布的直线基本重合，但两端的散点偏离直线的程度较明显，具有明显偏离正态分布的属性。

由ADF检验结果可知：钢铁期货收益率序列的ADF统计量的值为均远小于各自在1%，5%和10%的显著性水平下的临界值，ADF检验P值远小于0.01，说明钢铁期货收益率序列不服从单位根过程，为平稳序列。

2.2 VaR值的计算与检验

2.2.1 广义极值分布的VaR

利用广义极值分布,对我国钢铁期货的收益序列进行极大似然拟合，参数估计如表2所示。

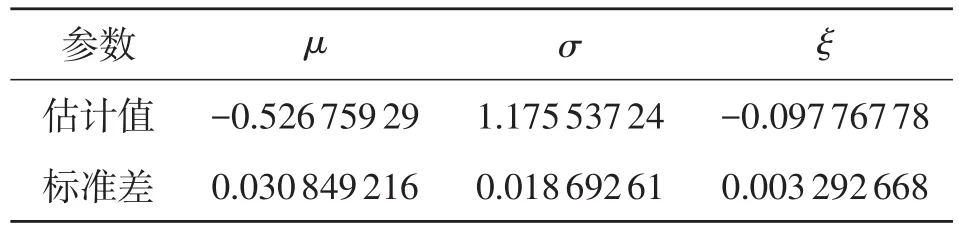
表2 广义极值分布参数估计表

对上述拟合结果作出模型诊断图（图2）。概率图、分位数图和重现水平图显示的拟合结果并不十分令人满意，最后概率密度曲线的估计和直方图是吻合的，因此只能近似认为拟合的模型是正确的。

图2 泸铜连三的收益率GEV拟合诊断图

根据拟合的参数估计值，计算出在95%，97%，99%，99.5%和99.9%置信水平下的VaR值（表3）。

表3 广义极值分布的VaR值计算结果

2.2.2 广义Pareto分布的VaR

采用峰度法对收益率序列进行处理，利用R统计软件编程得到阈值u为0.021 532 22，对超过阈值u的样本数据进行GPD分布拟合，得到序列参数的估计值为

同时，为了判断用GPD分布对残差序列尾部分布的拟合结果是否合理，分析分布拟合的程度如何，对分布的拟合情况进行诊断。对钢铁期货收益率序列超过阈值u为0.02153222的样本进行GPD分布拟合的诊断图如图3所示。从图3可以看出：钢铁期货收益率序列的散点基本都围绕参照线分布，且上尾的拟合效果更好，说明用分布来拟合钢铁期货收益率序列的尾部基本上比较合适。从图2 c和图3 c中也可以看出，估计的重现水平基本都在重现水平的置信区间内。因此，基于阈值进行的分布拟合效果较好。

得到参数的估计值后，可以计算得到钢铁期货收益率序列的VaR值，所得的结果如表4所示。

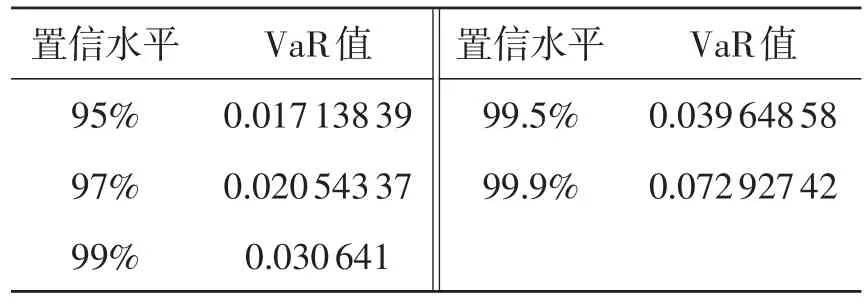
表4 广义Pareto分布的VaR值计算结果

2.2.3 广义Pareto分布的VaR

基于方差-协方差法的VaR模型、基于TARCH-VaR模型、基于极值理论的VaR模型以及基于TARCH-GPD-VaR模型在不同置信水平下的VaR值计算结果汇总如表5所示。

由表4～5可以看出：在同一种模型下，VaR的值随着置信水平的提高而增加，这个结论也可以从VaR的定义中得出，VaR值实质上是一个分布函数的高分位数，给定的置信水平越高，分位数的值越高，即VaR的值越大。由于表5中VaR值仅仅代表一系列值中一天的数据，仅仅对比一个值的大小并不能用来比较模型的优劣程度，因此用失败率回测检验方法来对模型进行回测检验。

图3 钢铁期货收益率序列分布拟合诊断图

表5 各种模型下钢铁期货收益率序列的VaR值

为了更直观地对比实际失败率P与期望失败率P*的大小，将失败率的对比转化为失败天数的对比，如果实际失败天数大于期望失败天数，则表明该模型低估了风险；如果实际失败天数小于期望失败天数，则表明该模型高估了风险。当实际失败天数与理论值接近时，认为模型较好地度量了风险水平。各种模型的失败率回测检验结果见表6。

表6 各种模型下钢铁期货收益率序列的失败天数

在较低的置信水平95%和97%下，基于TARCH-GPD的VaR模型在估计钢铁期货收益率序列时最有效，其计算的失败天数与理论检验值最接近；在较高的置信水平99%，99.5%和99.9%下，可以很明显地看出：方差-协方差法、TARCH法传统理论模型计算得到的失败天数均大于理论检验值，说明无论是基于正态分布的假设还是仅考虑序列的波动集聚性都存在低估尾部风险的情况。对于基于极值理论的模型得出的失败天数与理论检验值最接近；检验表明：基于极值理论的2个模型TARCH-GPD-VaR、GPD-VaR较为准确有效，且TARCH-GPD-VaR能在高低置信水平下都很好地刻画分布的尾部特征，优于传统的VaR模型。

［1］约翰，赫尔.期权、期货及其他衍生产品［M］.8版.北京：机械工业出版社，2011.

［2］唐成晓.基于极值理论的白银期货市场风险度量研究［D］.杭州：浙江工商大学，2012.

［3］胡晓馨.基于极值理论的黄金期货市场风险度量研究［D］.杭州：浙江大学，2014.

［4］Philippe Jorion.Valus at Risk:The New Benchmark for Managing Financial Risk［M］.McGraw-Hill,2006:15-18.

Study on Risk Measurement of Steel Futures Market in China Based on Extreme Value Theory

Chen Difang
（School of Sciences,Hubei University of Automotive Technology,Shiyan 442002,China）

Based on the model of extreme value theory and compared with different calculation models, the VaRs of the steel futures in China were obtained.The results show the model established by the ex⁃treme value theory can better describe the yield distribution characteristics of the tail,and is superior to the traditional VaR model.

extreme value theory;VaR（value at risk）;regression testing

T224

：A

：1008-5483（2016）04-0070-04

10.3969/j.issn.1008-5483.2016.04.016

2016-04-07

陈迪芳（1986-），女，湖北十堰人，硕士，从事金融数学与高级计量经济分析方面的研究。