三角函数全国课标Ⅰ卷试题分析及其备考教学策略

（福清市元洪高级中学，福建福州350300）

三角函数全国课标Ⅰ卷试题分析及其备考教学策略

刘细菊

（福清市元洪高级中学，福建福州350300）

三角函数作为高中数学的一个主干知识，是全国新课标I卷考查的重要内容，相关试题基础性强，有“型”可寻，认真研读这个章节的考纲内容，深入分析相关试题特点，引导学生整体掌握章节知识结构，合理归纳各类题型，重视思想方法的点拨，是高三备考复习教学的主要策略。

高中数学；三角函数；试题特点；题目类型

三角函数的周期性与奇偶性是现实数量与空间的一个重要模型，是中学数学学习中最重要的一种基本初等函数，它与代数、几何联系密切，是解决许多数学问题的有力工具，作为高中数学的一个主干知识，它也是全国新课标I卷考查学生基础知识与基本技能掌握情况的重点内容之一。历年来全国新课标I卷三角函数部分的试题重在考查基础知识、基本能力、基本思想，许多试题来源于课本中的例题、习题的变形。因此，立足教材，认真研读考纲内容，深入分析试题特点，引导学生整体掌握章节知识结构，合理归纳各类题型，把握思想方法，是高三备考复习教学的主要策略。

一、新课标全国I卷三角函数部分试题分析

2012-2016年新课标全国I卷三角函数部分的试题考点统计表

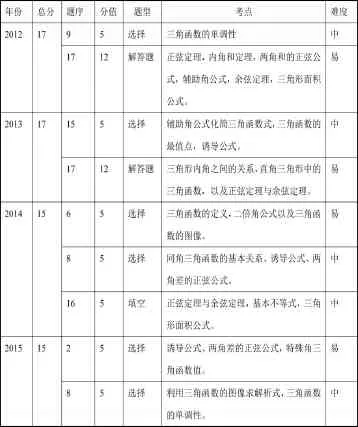
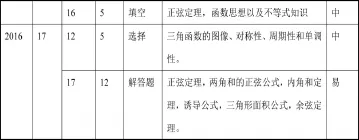
从上面的统计表不难看出，全国新课标I卷涉及三角函数与解三角形的考题所考查的主要内容是三角函数的基本概念、图像性质、“和、差、倍”公式的运用以及正、余弦定理。进一步分析试题所考查的数学思想方法内容，可以发现其重点承载的是函数与方程的思想、数形结合的思想、转化与化归思想的考查任务，同时，这一部分的试题难度定位一般是中、低档，题型比较稳定。

1.考小题“基础”凸显

(1)对于三角函数的图像和性质的小题，每年都考，其重点在于两域（定义域、值域、最值）、四性（单调性、奇偶性、对称性、周期性），以及用图（用三角函数的图像判断其性质）；对于三角函数的图像变换在近五年中都没有涉及到，但还需掌握好它。定义的考查频率不高，课标卷中，常将三角函数的定义与图象结合起来考查。

(2)对于三角恒等变换的小题考查频率高，其考查重点在于“化简”与“求值”。常利用已知角和被求角之间的关系，结合题目条件进行变形解决问题，需要熟练掌握各个公式，以及它们之间的联系，包括配凑思想、分类讨论思想等。

(3)对于解三角形，每年都考，其考题的位置一般不是在填空题的最后一题，就是在解答题的第一题，其重点是利用两定理解三角形，多以简单三角形的背景出现，有时以实际生活问题的背景呈现（2009年第17题解三角形的应用题）。

2.考大题有“型”可寻

有关三角形解答题，不是每年必考（五年三考），多与数列交替出现，其考查重点是以简单三角形为背景求三角形的边或内角或三角形面积有关的问题，考查难度中等，但需要有深度的推理、计算能力。一般利用正弦定理、余弦定理、面积公式可以得以解决。近五年的三角解答题虽没涉及到“以实际背景包装的三角应用问题”，但在2009年的全国卷中第17题的位置出现过，因此这块内容也应给予关注。

二、三角函数高三备考复习教学策略

认真研读《考试大纲》并细致分析历年全国新课标I卷真题，了解考纲中的内涵，熟悉考纲要求和全国卷试题特点，才能对复习教学进行合理定位，科学安排。

对三角函数基础知识的复习要做到广泛撒网，重点捞鱼。对概念、公式、性质不能走过场，要花足够的时间搞好主干知识的复习，应在“准确、系统、灵活”上下工夫，对知识要真正的理解和掌握并形成合理的知识网络，狠抓基础并重视思想方法的点拨，以不变应万变。

1.精选例题，帮助选择公式

三角函数这一主干板块公式众多，琳琅满目。一般校的学生基础较为薄弱，面对众多公式无从下手，如果能够有针对地精选例题，帮助学生归纳什么情况选哪个公式，让学生有“路”可套，这样就能达到事半功倍的效果。

【例】（1）在△ABC中，已知b=10，c=56,C=60°，求角B；

（2）已知锐角△ABC的内角A,B,c的对边分别为a,b,c,23cos2A+cos2A=0，a=7，c=6则b=()

A．10B．9C．8D．5

这两个题目都是已知两边及其中一边的对角，第一题求角，第二题求边，很多教辅书把这两个题目归结正弦定理题型。实际上这两个题目第一题用正弦定理，第二题用余弦定理更简单，因此在复习过程中要借助例题引导学生总结归纳：

（1）已知两角一边解三角形用正弦定理；

（2）两边及其中一边的对角求角用正弦定理，求边用余弦定理；

（3）已知两边夹角解三角形用余弦定理；

（4）已知三边解三角形用余弦定理；

（5）使用三角形面积公式的规律：已知哪个角就选择有那个角的面积公式；

（6）使用余弦定理的规律：已知哪个角就选择有那个角的余弦公式。

这样，学生在利用公式的时候，就可以从这里找到“套路”。

2.关注核心，重视思想方法

数学思想和方法是数学知识在更高层次上的抽象和概括，在全国新课标I卷当中三角函数部分重点承载的是函数与方程的思想、数形结合的思想、转化与化归思想，在备考过程中，必需关注数学思想方法的渗透，灵活地借助数学思想方法解题，就可以避免繁杂的运算，优化解题思路，降低解题难度。

分析：本题考查同角三角函数关系式，可运用方程思想：（1）解出sinθ，cosθ的值；（2）可利用sinθ+cosθ,sinθ-cosθ,sinθ·cosθ,之间的关系，求出sinθ—cosθ,组成方程组进行求解。

评析：通过建立方程或方程组，并求出未知量的值，从而使问题得到解决，本题利用方程思想解题。

分析∶本题根据函数解析式，画出图象，可以直观而简明地得出答案，在有时间限制的高考中就能大大地节约时间，提高考试的效率。

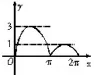
评析：本题考查零点定理的应用，利用数形结合思想可以很快使问题得到解决。

分析：本题考查三角恒等变换中已知值求值，通过观察已知角和被求角之间的关系，利用化归转化的思想使问题得到解决。

评析：考查角的配凑，利用化归转化思想方法可以使问题轻松得到解决。

3.把握热点，帮助归类

从这五年的试题分析可以看出，三角部分核心内容年年考，重点内容重点考，解三角形是高频考点，每年都考，不是在填空题的最后一题就是大题第一题，题型主要归纳为以下几类。

类型1.活用两个定理（知三求一）

这类题目特点是：已知有三个边角关系，求三角形中的其他元素。活用两个定理可以一步到位。

【例】(2016全国II理13)△ABC的内角A,B,C的对边分别为a,b,c，若cosA=，cosC=，a=1，则b=_____。

类型2．借助两个定理边角互化统一（已知等式关于边或角的正弦齐次）

这种类型题目特点是∶已知关于边或角的正弦齐次式，无法利用两个定理一步到位，但利用正弦定理统一化为边或统一化为角。

【例】（2016全国I理17）△ABC的内角A,B,C的对边分别别为a,b,c已知2cosC(acosB+bcosA)=c，（I）求C；（II）若c=7,△ABC的面积为，求△ABC的周长。

类型3．借助两个定理建立相关参数的方程或函数（求值列方程，求最值或范围列函数关系式）

这种类型特点是：题目给出的条件不够，需要我们去创造条件，引进参数列出方程求解或列出三角函数关系式，利用三角函数的有界性求最值或取值范围。重在考查学生方程与函数思想。

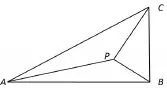
【例】（2013新课标I理17）如图，在△ABC中，∠ABC＝90°，AB=3，BC=1，P为△ABC内一点，∠BPC＝90°，

(1)若PB=12，求PA；

(2)若∠APB＝150°，求tan∠PBA。

类型4.解三角形在实际生活中的应用

三角函数模型的应用近几年全国课标理科卷中出现频率不高，但是2009年考过，所以也必须关注。这种题目就是把它的外衣脱掉，建立三角模型，将所给的条件转化到一个三角形中去求解。

4.规范作答，力争高分

在复习时，除了要抓好知识、题型、方法等方面的教学外，还应该提升学生的解题规范，常抓易失分的点。比如：已知值求角一定要说明角度范围，单调区间有多个不能用“⋃”，求单调区间时“KϵZ”不能丢等等。三角函数的得分一方面取决于对问题的理解、求解，另一方面取决于作答的规范、步骤等。因此要加强每天一题规范训练，全面批改，落实订正。

总之，三角函数是初等数学的重要内容，在数学和其他领域中具有重要作用。它是解决数学问题的重要工具。从这五年的全国高考课标卷来看，三角函数的题型始终保持稳定，小题偏向考察三角函数性质和三角恒等变换的化简求值，大题偏向考察解三角形，我们把握好这些特点，把它正确定位，广大师生能从中寻觅、体会课标卷命题的“周期性”等规律，从而实现高效备考。

［1］傅殿松.高考数学三角函数复习专题分析［J］.中学教学参考，2016(2)．

［2］蒋科新.三角函数解题思想方法［J］.中学教学参考，2016 (11)．

（责任编辑：王钦敏）