关于单摆运动的数值模拟与分析

孙 进，丁宗玲

（安徽大学，安徽 合肥 230601）

关于单摆运动的数值模拟与分析

孙 进，丁宗玲

（安徽大学，安徽 合肥 230601）

单摆在物理教学中是较为常见的实验器件.在大学物理中对于它的研究主要局限在初始摆角很小情况下的简谐运动.在本文中我们摆脱对初始摆角的局限，采用四阶Runge-Kutta方法对于单摆的运动方程直接进行数值计算，考虑了无阻力和有阻力两种情况下，从角位移、角速度随时间变化的规律，周期、能量等方面来分析探讨单摆的运动.

单摆；四阶Runge-Kutta；周期；动能；机械能

1 引言

一根不会伸长的细线，上端固定，下端悬挂一个很小的重物，把重物移动后就可以在竖直平面内来回摆动，这种装置称为单摆.单摆是生活和物理研究中较为常见实验装置.对于单摆运动规律的研究，在大学物理教学里面一般都是把它放在简谐运动这一章节中讲解，从牛顿第二运动定律出发，最后能够解析求解出摆球运动的角位移随时间按照余弦规律变化，因而单摆的运动是简谐运动[1].但是我们知道，只有当单摆的初始摆角小于5度时，它的运动才属于简谐运动，而在其它的情况下，由于运动方程很难解析求解，解的形式也较为复杂，因而它的运动特征在大学物理教科书上很少提到.

随着计算机的普及运用，对于一些复杂物理问题的数值模拟变得越来越简单.通过计算机语言和一些作图软件，可以很轻松的绘制出物体运动的轨迹以及各个物理量的变换曲线，更加直观的展现出物体的运动规律，从而可以帮助学生更好的理解一些物理问题.

我们知道单摆的牛顿运动方程实际上是二阶常微分方程.已知了初始条件的情况下，在数值计算中这就是一个解微分方程的初值问题，有很多方法都可以对其进行求解[2].因而在这篇文章里，为了能够帮助学生更加全面了解单摆的运动过程，弄清楚一般振动与简谐运动的区别，我们采用数值计算的方法，从牛顿第二定律出发，不做任何近似，直接对单摆的运动方程进行数值求解和模拟，从而对单摆在一般情况下运动进行细致的研究.

2 在小摆角情况下的解析解

以铅直位置作为振动的平衡位置，假设某一时刻摆线偏离铅直位置的角位移为θ，并规定逆时针方向为角位移的正方向.同时假设摆球的质量为m=1kg,而摆线的长度为l=1m.摆球的切向加速度为

单摆在运动过程中，受到重力、阻力以及重力的作用.所受的阻力主要来自于空气，当运动速率不是太大时，阻力与速率成正比，方向沿切线方向，即

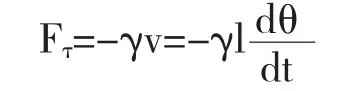
其中γ为比例系数.在切向方向，根据牛顿第二定律，得

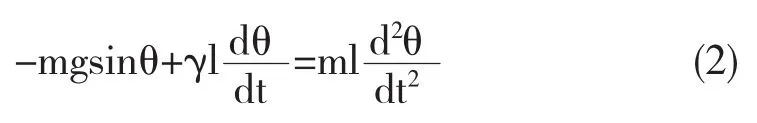
公式中的负号说明重力沿切向方向的分力与角位移θ反向.在不考虑阻力的情况下，γ=0，当θ＜5°时，sinθ≈θ，从而得到

可见在这种假设下，单摆的运动为简谐运动，并且简谐运动的角频率只与摆线的长度和重力加速度有关，和摆球以及摆角没有关系[1].

3 数值计算方法

在θ＜5这一前提假设不成立的情况下，公式(2)的解析求解就没有这么简单了.为了能够全面的了解单摆的运动规律，我们采用数值方法对其进行计算模拟.在已知t=0时刻的初始摆角以及初始速度的条件下，方程(2)的求解在数值计算方法中就是典型的初值问题.这里一个我们首先采用降阶法[3]对公式(2)进行降阶，使其变成一阶常微分方程组.引入变量y1和y2,令

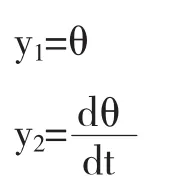
由公式(2)，可以得到

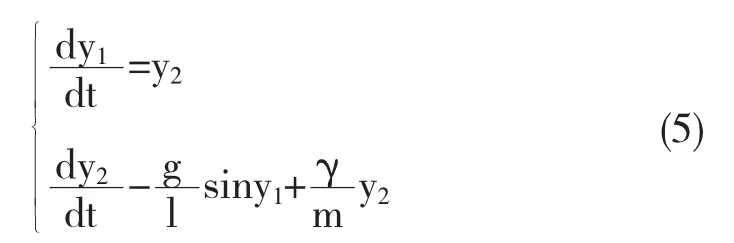
通过以上变换我们就将一个二阶的常微分方程转变成了一阶的常微分方程组.在数值计算方法中，四阶Runge-Kutta[2]是一种公认较为精确的方法，它可以用来求解一阶的常微分方程以及一阶常微分方程组.在这篇文章中，我们采用四阶Runge-Kutta方法数值求解方程组（5），从而得到角位移θ以及角速度dθ/dt.

4 数值计算结果与分析

首先我们忽略阻力的作用，设γ=0考虑单摆只受到重力的作用.图1-2绘制了不同的初始摆角的情况下，角位移以及角速度随时间的变化规律.我们首先计算初始摆角为非常小的情况，将数值计算的结果与其解析解进行了比较.图1显示当θ0=π/60＜5°时，我们发现数值计算的结果与理论推导值公式(4)符合的非常好，从而说明我们计算方法的正确性.同时我们的结果也形象的证明在小摆角的情况下，单摆运动的角位移随时间是按照余弦规律变化的，因而在这种情况下将单摆的运动看成是简写振动是合理的.

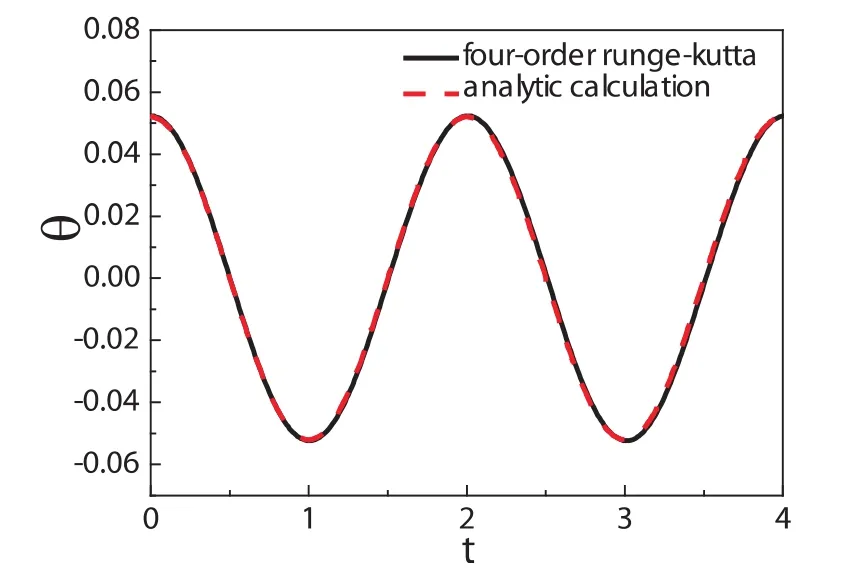
图1 当初始摆角θ0=π/60时，四阶Runge-Kutta数值计算结果(黑色实线)与解析结果(红色虚线)

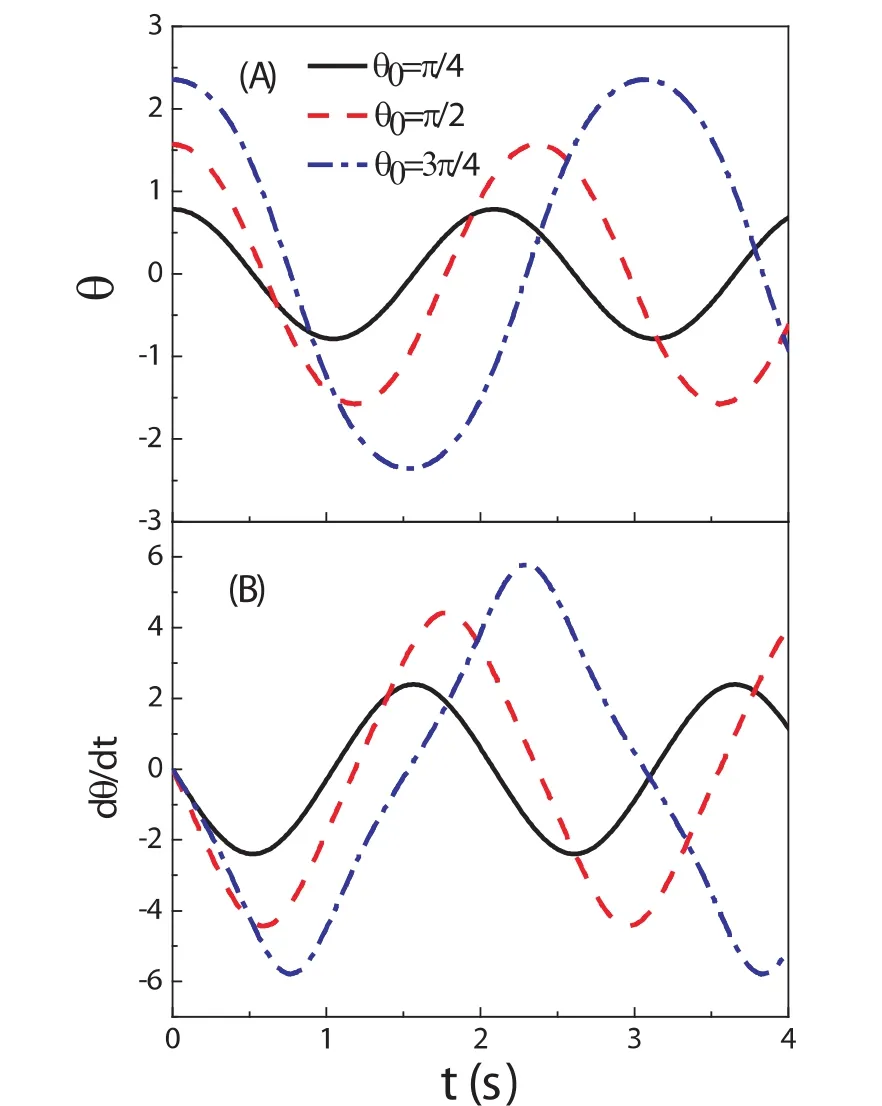
图2 (A)不同的初始摆角数值计算出的角位移随时间的变化；(B)不同的初始摆角数值计算出的角速度随时间的变化

接下来，我们将初始摆角逐渐增大.随着摆角的增大，当初始摆角大于5度，但小于180度时，sinθ≈θ成立的条件已经不符合，因而方程（4）已经不能够描述单摆的运动了.我们希望在这种情况下也能够形象的刻画出单摆的运动规律.图2为不同的初始摆角时，角位移以及角速度随时间的变化关系.很明显，三种不同的初始摆角，对应的角位移和角速度仍然是随时间做周期性运动的.但是仔细对比我们发现此时θ随时间的变化规律已经不是按照正弦或余弦函数了，随着初始摆角θ0的增大，这种差异变得越来越明显.当θ0=3π/4时，图2绘制出来的不论是角位移还是角速度的图形与余弦函数比起来已经有了很明显的变形.因而在这种情况下，单摆的振动虽然是周期性的，但已经不是简单的简谐运动了.

此外，从图2中我们也发现除了随时间变化的函数形式不再是余弦或正弦函数，振动的周期也不会像简谐运动是固定不变的，它会随着初始摆角的不同而发生变化.在对计算公式没有任何近似的情况下，四阶Runge-Kutta数值计算方法求解出来的结果显示，但θ0很小的情况下，周期的变化并不明显，这种情况对应着简谐运动中的固有周期.然后随着θ0的增大，周期的变化开始显现出来，它会随着初始摆角的增大而增大，同时变化的速度也会越来越快.

我们也考虑了能量的变化.我们知道，在单摆运动的过程中，动能为

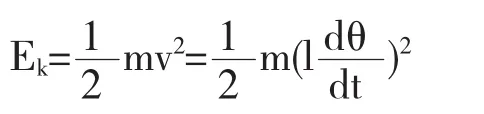
以摆球达到的最低点作为重力势能的零势能点，摆球运动过程中的势能为Ep=mgh=mgl(1-cosθ).

能量的变化跟简谐振动相似，不论是动能还是势能随时间都做周期性变化.位移最大时，时能最大，动能为零，反之亦然.由于是保守系统，单摆的总机械能是常量.

实际上在单摆运动的过程中，并不能保持能量守恒，主要是因为它会受到阻力的作用，从而产生能量的耗损.为了能够更全面真实的了解单摆的运动，我们进而考虑了在运动过程中的阻力作用.

当考虑阻力的情况下，我们发现当存在阻力时，但阻力不是很大时，单摆的摆动不再是一成不变的，摆动的幅度会随着时间逐渐减小，最终趋于零，摆动停止这即为欠阻尼状态[4].随着阻力的增大，从开始到停止的时间逐渐变短，如果阻力足够大，我们发现单摆不会出现来回摆动的情况，角位移直接变为零，即第一次到达平衡位置就停止了，这也就是我们经常说的过阻尼状态[4].

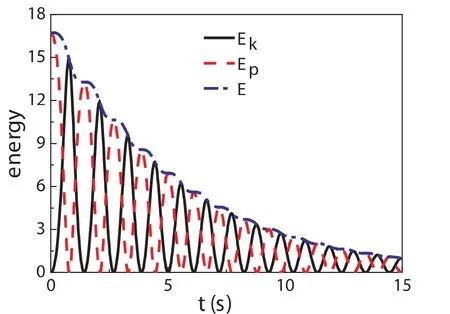
图3 γ=0.2时，单摆动能、势能以及机械能随时间的变化

除了单摆的摆幅随时间减小，最后达到零，单摆运动过程中能量也会在阻力中耗损.图3非常清晰的显示，不论是动能还是势能，在摆动的过程中，它们的总和机械能都在逐渐减小的，当单摆最终停止时，总机械能为零.

5 总结

在这篇文章中我们用四阶Runge-Kutta方法对单摆的运动方程进行了数值求解.希望能够通过完整的求解单摆的运动方程以及模拟作图，清晰直观的展示单摆运动的规律，帮助学生透彻的了解单摆的振动过程.通过计算模拟，我们发现在不考虑阻力的情况下，当初始摆角很小的情况下，数值计算的结果与余弦函数符合的很好，这也正是在大学物理教学中将单摆的运动归纳为简谐运动的原因.将初始摆角增大以后，我们发现单摆的运动虽然会始终保持着周期运动的规律，但不论是角位移还是角速度随时间的变化规律都可以很明显的看出不再是余弦或正弦函数了，因而在这种情况下，单摆的周期性振动已经不再是简谐运动了.对于其周期的研究更是说明了两种运动的差异.同时由于没有考虑阻力的作用，单摆可以看成是孤立系统，因而其运动过程中动能势能可以相互转换，机械能不变.但是机械能在考虑了阻力的作用后就不再守恒了，动能和势能在振荡中逐渐减小直至为零，单摆停止摆动.随着阻力的增大，单摆摆动的时间逐渐缩短，当阻力足够大时，单摆从初始摆角开始直接到达平衡位置静止，不会出现振动现象，即为过阻尼.

〔1〕韩家骅，汪洪.大学物理学[M].合肥：安徽大学出版社，2006.

〔2〕Richard L.Burden,J.Douglas Faires.数值分析[M].北京：高等教育出版社，2000.

〔3〕顾昌鑫，朱允伦，丁培柱.计算物理[M].上海：复旦大学出版社，2005.

〔4〕漆安慎.杜婵英.力学[M].北京：高等教育出版，2009.

O411

A

1673-260X（2016）12-0004-03

2016-09-12

国家自然科学基金青年基金（11304001）；教育部博士点基金新教师类项目（20133401120002）；安徽省教育厅自然科学基金重点项目（KJ2013A035）