库莫洛光学测量颗粒浓度方法的研究
2017-01-10苏杭丽赵文彦卢永生
苏杭丽,毛 波,2,赵文彦,卢永生
(1.南京财经大学信息工程学院,江苏南京210023;2.江苏省现代粮食流通与安全协同创新中心,江苏南京210023;3.河海大学电气学院,江苏南京 210098)
库莫洛光学测量颗粒浓度方法的研究
苏杭丽1,毛 波1,2,赵文彦1,卢永生3
(1.南京财经大学信息工程学院,江苏南京210023;2.江苏省现代粮食流通与安全协同创新中心,江苏南京210023;3.河海大学电气学院,江苏南京 210098)
在光学方法测量颗粒浓度时,测量的精度受颗粒粒径和颗粒颜色等因素的影响.为解决这一问题,现将颗粒的浓度、粒径和颜色三个相关联的量统一在一起进行研究,建立包含这三个属性的浑匀液体库莫洛消光散射方程.根据库莫洛前向散射消光方程可以求出受粒径影响的颗粒浓度;给出散射消光系数、吸收消光系数及有效光密度的表达式;解决Beer消光定律在实际应用中受粒径变化、颗粒浓度超限的影响.最后,用较完整的实验证明库莫洛消光散射理论是正确的.
泥沙测量;前向散射;颗粒粒径;颗粒浓度
1 引言
粉体颗粒浓度的现场测量是很复杂的问题,测量原理涉及多个领域[1~7].在应用最多的光电测量颗粒浓度的方法中,电子学的部分如电路设计、计算等较易实现,难的部分在于光学原理.光学部分以Beer消光定律[8~10]为基础,但Beer定律在测量泥沙浓度的应用中存在着一定的局限性.首先,Beer定律本身受线性范围影响,不适合泥沙现场的非线性应用;其次,颗粒浓度的测量中含有颗粒粒径的影响[11~13],而颗粒粒径(如河流泥沙、粉体颗粒等)的现场测量很困难.
作者将颗粒的浓度、粒径和颜色三个属性放在一起进行研究,结合Kumbelka-Munk方程[14]和Beer定律以及颗粒物理属性的相关理论,找出颗粒浓度与粒径之间的数学关系,从理论上给出了悬浮液中受粒径影响的颗粒浓度的计算方法,并经过实验室实验证明所给出的关系式是正确的.
2 库莫洛方程
作者在Kumbelka-Munk方程的基础上推导出式(1)的一维距离消光方程组:
(1)
其中,i为后向散射仪收到的光强,j为前向散射仪收到的光强,QS为散射消光系数,QB为吸收消光系数,SK为侧向散射消光系数.
(1)式称为库莫洛(Kumbelka-Munk-Lu,简称KML)消光方程组,解为(2)式:
(2)
在单光源、平行光、定距离(即i0=0、x=)时,测得的浑液颗粒浓度为c的情况下,(2)式简化为(3)式:
(3)
其中,I0为处后向散射的杂散光强度,α′为总浓度消光系数,系数α′与α同为消光系数,但数值不同,ξ为系数.
(3)式第一个方程称为KML前向散射方程,第二个方程称为KML后向散射方程.通过KML后向散射方程可以求出颗粒粒径[14].本文通过KML前向散射方程,求出悬浮液中受粒径影响的颗粒浓度.
3 前向散射消光方程的两项研究
3.1 前向散射消光系数的研究
3.1.1QS的实验计算
当浓度很低时,光的吸收效应小散射效应大,KML前向散射消光方程为:
j=j0e-Qsc/d
(4)
由式(4)求出QS,得:
(5)
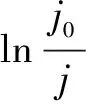
3.1.2QS的理论计算
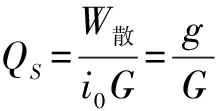
其中,W散为散射掉的总能量,g为粒子光照影子截面积,G为颗粒子几何截面积.
(6)
其中,S(0)为散射角θ为0时的散射振幅函数,Re[S(0)]为S(0)的实部,λ为波长.
根据颗粒粒径大小及颗粒对水相对折光系数的大小,将QS分为13个区,可以求出其特解.根据“透明粗粒”模型[13]进一步推导后得到(7)式:
(7)
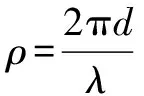
经波长修正得:
(8)
再经光路的修正及选取适合实验数据的参数求出QS,得:
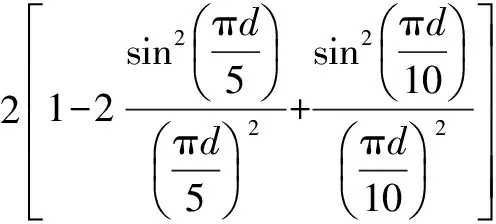
(9)
3.1.3QB的计算
(10)
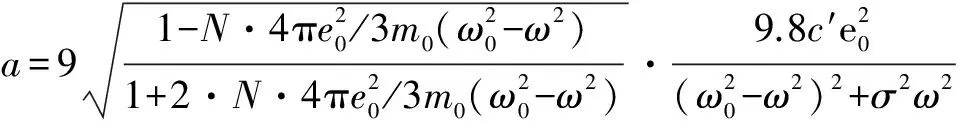
以上研究限于浑液系统只发生一次散射,QB值很小,可以忽略不计.如果浑液浓度再增大,系统发生了多次散射现象,则散射系数相对减小,而吸收系数会相对增加,但结果不影响散射与吸收的规律.
3.2 前向散射消光定律的非线性及其校正
3.2.1 前向散射消光定律的非线性
无论是Beer定律还是广义的Beer定律都存在一个非线性的问题,即浓度c增大后,光密度Y与c的关系无一例外都偏离直线.这是由于浓度增大后,颗粒对光作用的独立性被破坏,即部分颗粒被其他颗粒所阻挡导致其失去与光作用的机会,即所谓发生了重影.处于重影中的粒子失去了作用的独立性.
消光微分方程如下:
(11)
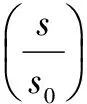
在实际应用中,当浓度很大时,需要对Beer定律微分方程进行修正.
3.2.2 修正后的前向散射消光方程
重影概率修正后的前向消光方程为:
(12)
两边积分得:
(13)
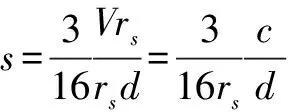
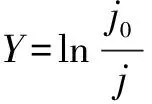
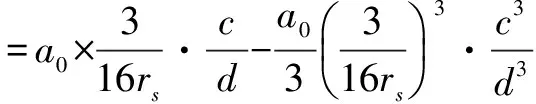
(14)
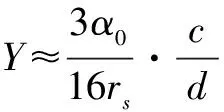
(15)
其中,B≈0.3~0.055.
令YB=YeBY2,YB称为有效光密度,式(15)可写为式(16):
(16)

3.3 白钢玉粉体浓度的KML法测定
实验样品采用予南粉厂生产的白钢玉粉体系列,共有W40、W28、W20、W14、W10、W7、W5、W2.5、W1九个样品,下标表示中值粒径,比重约为3.3g/L,等效波长λe为720nμ,仪器缝宽4mm,样品盒长40mm.
实验得到图1和图2中光密度Y与浓度和粒径的对应曲线.
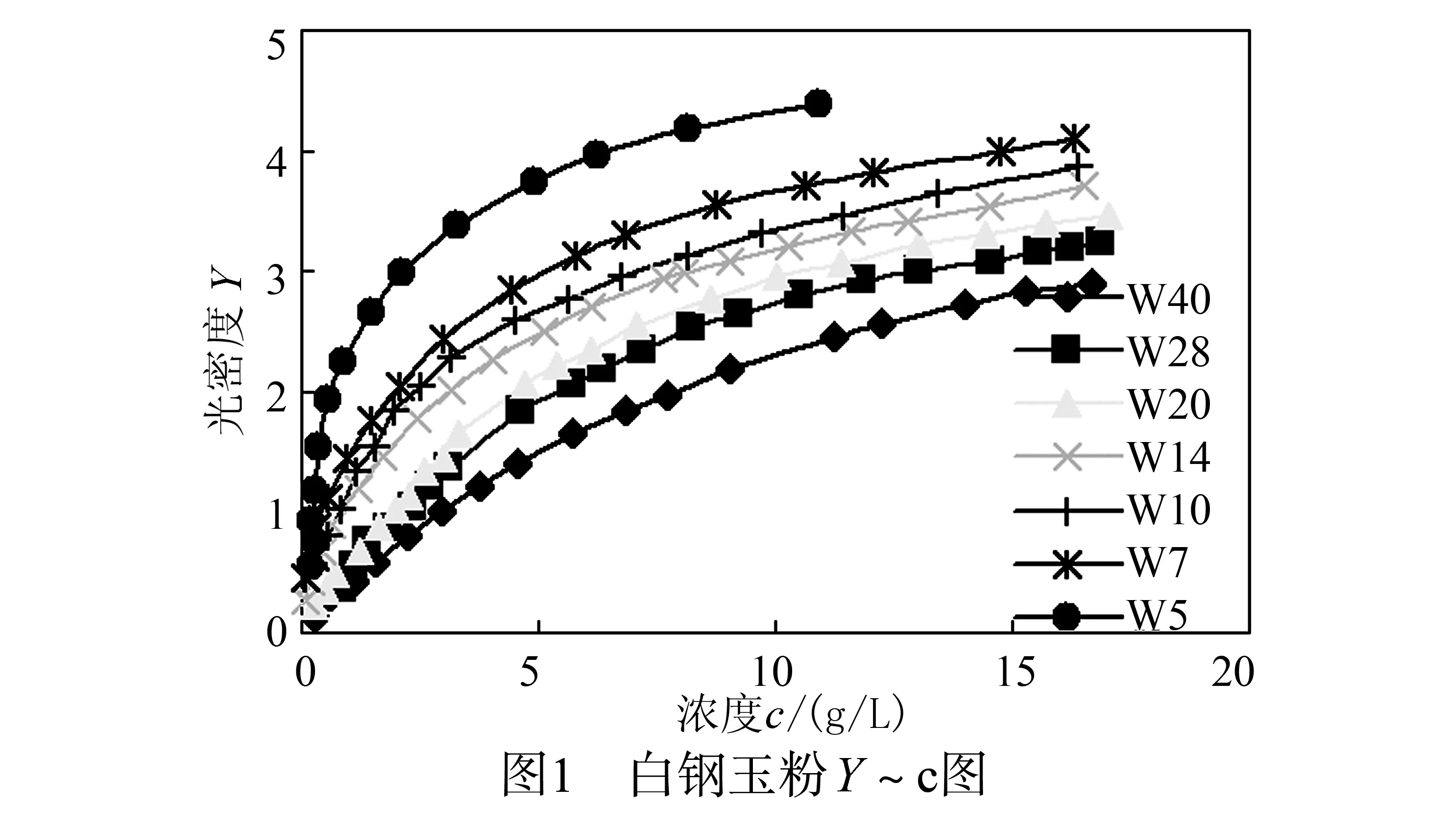
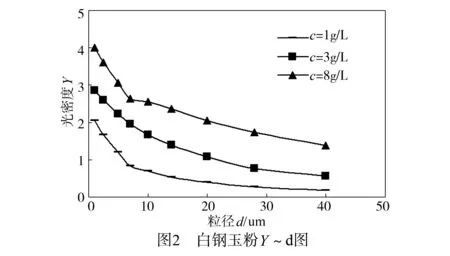
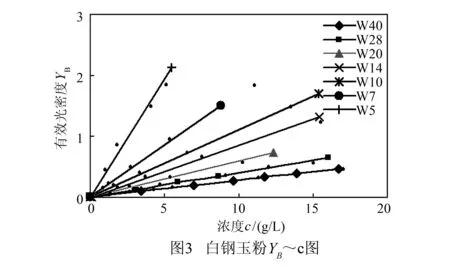
图2中存在非线性,修正后的有效光密度YB与浓度之间的关系见图3.实验中,B取0.055.图3的YB~c基本成一直线族,说明(16)式是正确的,KML前向散射消光方程是可以求出悬浮液中受粒径影响的颗粒浓度.
4 结论
(1)本文的库莫洛光学方程组将悬浮液中颗粒的浓度、粒径和色度三个属性统一在一起进行研究,给出散射消光系数,吸收消光系数和有效光密度的表达式.这些是光学测量颗粒属性理论上的一个补充.
(2)库莫洛方法考虑了浑匀液体中颗粒浓度、粒径、色度间的相互影响,因此测量结果更准确.库莫洛方法不仅可以求出悬浮液中颗粒的浓度,还可以求出颗粒的粒径和色度.
(3)本文侧重于理论分析.实验是在室内环境下的浑匀液体中进行的.希望本文能对颗粒浓度的现场实测以及测量工具的研制有所帮助.
[1]Richard L M,Brent A M.Using MODIS terra 250m imagery to map concentrations of total suspended matter in coastal waters[J].Remote Sensing of Environment,2004,93(1/2):259-266.
[2]Ha H K,Hsu W Y,et al.Using ADV backscatter strength for measuring suspended cohesive sediment concentration[J].Continental Shelf Research,2009,29(10):1310-1316.
[3]苏杭丽.超声波在悬浮液中的衰减[J].河海大学学报,2012,40(6):710-714. SU Hang-li.Ultrasonic attenuation in suspension [J].Journal of Hohai University:Natural Sciences,2012,40(6):710-714.(in Chinese)
[4]朱维庆,朱敏,等.声学悬浮泥沙浓度估计[J].中国科学A辑,2001,31(5):459-465. ZHU Wei-qing,ZHU Min,et al.Estimation of acoustic suspended sediment concentration[J].Science in China:Series A,2001,31(5):459-465.(in Chinese)
[5]李洪灵,张鹰,等.基于遥感方法反演悬浮泥沙分布[J].水科学进展,2006,17(2):242-245. LI Hong-ling,ZHANG Ying,et al.Study on the inversion model for the suspended sediment concentration in remote sensing technology[J].Advances in Water Science,2006,17(2):242-245.(in Chinese)
[6]Fontaine T A,Moore T D,et al.Distributions of contaminant concentration and particle size in fluvial sediment[J].Water Research,2000,34(13):3473-3477.
[7]Ha H K,Maa J P Y,et al.Estimation of high-resolution sediment concentration profiles in bottom boundary layer using pulse-coherent acoustic Doppler current profilers[J].Marine Geology,2011,279(1-4):199-209.
[8]凤宏晓,侯彪,等.基于非下采样Contourlet 域局部高斯模型和MAP的SAR图像相干斑抑制[J].电子学报,2010,38(4):811-816. FENG Hong-xiao,HOU Biao,et al.SAR image despeckling based on local gaussian model and MAP in NSCT domain[J].Acta Electronica Sinica,2010,38(4):811-816.(in Chinese)
[9]谢世朋,罗立民.基于衰减板的锥束CT 散射校正[J].电子学报,2011,39(7):1708-1711. XIE Shi-peng,LUO Li-min.Scatter correction for cone beam CT using attenuation baffle [J].Acta Electronica Sinica,2011,39(7):1708-1711.(in Chinese)
[10]吴家坤,卢永生,王锡弟.新型宽域粒度分析仪[J].河海大学学报,1989,17(6):101-106. Wu Jiakun,Lu Yongsheng,Wang Xidi.A new type wide range particle size analytical instrument[J].Journal of Hohai University(Natural Sciences),1989,17(6):101-106.(in Chinese)
[11]卢永生,徐友仁,等.微粒散射消光系数的测定及理论[J].河海大学学报,1996,24(4):53-57. LU Yong-sheng,XV You-ren,et al.Measurement and theory of extinction coefficient of particle scattering[J].Journal of Hohai University(Natural Sciences),1996,24(4):53-57.(in Chinese)
[12]Douglas A Skoog,F.James Holler,et al.Principles of Instrumental Analysis[M].Belmont,CA:Thomson Brooks/Cole cop,2007.
[13]H C van de Hulst.Light Scattering by Small Particles[M].New York:Dover Publications Inc,1981.
[14]苏杭丽,卢永生.库莫洛后向消光理论在测量颗粒粒径中的应用[J].电子学报,2014,42(4):736-739. SU Hang-li,LU Yong-sheng.Measurement of particle size by KML back extinction equation [J].Acta Electronica Sinica,2014,42(4):736-739.(in Chinese)

苏杭丽 女.1973年5月出生于山东荣成.博士、副教授,主要研究方向为自动化技术、计算机应用.
E-mail:su-hl@163.com
毛 波 男.毕业于瑞典皇家理工学院,获得博士学位,目前担任南京财经大学信息工程学院副教授,主要研究方向为地理信息系统,三维综合与可视化技术,数据挖掘等.

赵文彦 男.1972年出生于江苏高邮.硕士、讲师,研究方向为计算机图形学、计算机辅助设计与制造.
E-mail:zwy158@163.com
卢永生 男.1935年生于浙江温州市.河海大学教授,主要研究方向为水利量测技术及其自动化,研制的河流泥沙颗分仪得到广泛应用.
E-mail:luyongsheng35@163.com
Measurement of Particle Density by KML Forward Extinction Equation
SU Hang-li1,MAO Bo1,2,ZHAO Wen-yan1,LU Yong-sheng3
(1.SchoolofInformationEngineering,NanjingUniversityofFinanceandEconomics,Nanjing,Jiangsu210023,China; 2.CollaborativeInnovationCenterforModernGrainCirculationandSafety,Nanjing,Jiangsu210023,China; 3.CollegeofElectricalEngineering,HohaiUniversity,Nanjing,Jiangsu210098,China)
The measurement of particle density is affected by particle size and color in the optical method.The Kumbelka-Munk-Lu equations were built that contained the variables of particle density,size and color.The value of particle density affected by particle size could be derived by the forward scattering extinction equation of the Kumbelka-Munk-Lu equations; The scattering extinction coefficient,the absorption extinction coefficient and the effective optical density equation were given.The problem was solved that the Beer extinction equation was affected by particle size and density.The experiments were done to test the Kumbelka-Munk-Lu equations.
sediment measurement; forward scattering; particle size; particle density
2010-07-15;
2016-09-08;责任编辑: 郭游
江苏省高校优秀中青年教师和校长境外研修计划资助; 国家自然基金(No.41671457);国家粮食局的粮食公益项目(No.201513004);国家科技支撑计划(No.2015BAD18B02,No.2015BAK36B02);国家电子商务信息处理国际联合研究中心项目(No.2013B01035);江苏高校优势学科建设工程资助项目
TN29
A
0372-2112 (2016)12-3032-04
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.12.031
