基于松弛交替投影的MIMO雷达相位编码波形设计

冯 翔,陈志坤,李风从,赵宜楠

(哈尔滨工业大学电子与信息工程学院,黑龙江哈尔滨150001)

基于松弛交替投影的MIMO雷达相位编码波形设计

冯 翔,陈志坤,李风从,赵宜楠

(哈尔滨工业大学电子与信息工程学院,黑龙江哈尔滨150001)

任务场景日趋复杂给MIMO(Mutiple-Input Mutiple-Output)雷达带来诸多挑战.为应对强散射体遮蔽干扰、阵元间波形互扰及特定频带干扰等复杂电磁环境,该文提出一种松弛迭代谱拟合交替投影算法来设计相位编码波形.该算法基于功率谱拟合及交替投影框架,并引入扩展的加速因子；首先,凭借功率谱与非周期相关函数的傅里叶变换关系,将相关特性拟合问题转化为功率谱近似问题；然后,构建理想波形频谱并利用松弛机制扩展优化投影区；最后,利用快速傅里叶变换及加速交替投影机制迭代优化.计算机仿真表明,该算法运算效率高、可有效避免局部停滞,与当前流行算法相比更适合在线波形设计.

MIMO雷达；波形设计；功率谱逼近；相位编码；交替投影

1 引言

为应对复杂任务场景,雷达自适应性显得尤为重要.波形分集可视为自适应性的一种体现且成为目前研究的热点[1～3].对于MIMO雷达而言,波形分集既能提高目标识别能力又能提高分辨力,成为提升雷达自适应性的重要切入点[4～6].避免强散射体遮蔽干扰需发射波形具备较低的自相关旁瓣；降低MIMO雷达阵元间相互影响要求发射波形具有低自、互相关旁瓣特性；抑制特定频带电磁干扰要求发射波形频谱具备稀疏特性；另外,为充分利用发射机功率,恒模特性亦成为客观要求[7].

文献[8]针对恒模波形设计提出循环类算法,其利用相关函数与功率谱之间的傅里叶变换关系来迭代优化所定义的目标函数,该类算法耗时长、相关旁瓣较高而难以满足实际需要；但其给后续研究带来了众多启示.文献[9]利用循环算法求解最小化加权积分旁瓣电平和功率谱密度问题以获得满足峰均比约束的波形；文献[10～12]引入交替投影框架来获取满足需求的恒模波形,但算法初始化导致求解稳定性较差而影响收敛.文献[13]利用序列二次规划与加权迭代方法求解波形设计问题,但在多阵元情形计算复杂度较高且易出现梯度矩阵奇异而难以收敛.文献[14]利用改进遗传算法设计MIMO雷达波形；文献[15]针对遗传算法、粒子群算法等提出改进策略；但该类算法往往因群体多样性较差而收敛停滞.因此,恒模约束下耗时少、稳定性高且具有较佳性能的算法成为当前波形设计的迫切要求.

该文基于功率谱拟合与交替投影框架,引入松弛迭代谱拟合交替投影算法(RISAAP,Relaxed Iterative Spectrum Approximation Alternating Projection method),着力解决MIMO雷达复杂场景问题.此算法利用功率谱与非周期相关函数的傅里叶变换关系,将相关函数拟合问题转化为功率谱近似问题,依靠松弛机制扩展集合优化投影区,凭借快速傅里叶变换在时域、频域交替迭代优化.该算法运算效率高、可有效避免局部停滞且有较高鲁棒性,与当前流行算法相比更适合在线波形设计.

2 问题描述与分析

假定具有M个发射阵元的MIMO雷达系统,其基带恒模相位编码波形矩阵可表示为:

X=[x1x2…xM]∈N×M

(1)

其中,第m个阵元的发射波形序列可表示为xm=[ejψ1ejψ2… ejψN]T,ψn∈[0,2π)为编码相位,N为序列码长.考虑到接收端滤波器输出可视为波形相关函数与雷达场景的卷积,那么可令α(x)=[α0(x) …αN-1(x) 0α-N+1(x) …α-1(x)]T表示某阵元波形的自相关函数序列；假定感兴趣的待测目标位于第q个距离单元,那么第l个单元中的强散射体可能会对第q个单元目标造成干扰,进而影响目标检测,而这种影响是通过波形自相关旁瓣来实现的[12].为最小化强散射体旁瓣影响,应使发射波形的自相关函数序列满足如下条件:

(2)

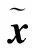
另外,MIMO雷达阵元间波形互扰严重影响雷达获取目标信息的性能,为抑制各阵元波形间互扰,即需设计波形具有低自、互相关旁瓣特性[10].以第n个采样延时的发射波形相关矩阵Rn(X)为例(Rn(X)=(XHU(n)X)T,U(n)表示偏移矩阵,(·)H表示共轭转置),其非主对角线元素应尽可能逼近零,而主对角元素应逼近理想波形自相关表示:

(3)

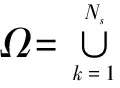
(4)

(5)

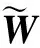
3 波形设计

3.1 目标函数构造

首先,对于抑制强散射体旁瓣遮蔽问题,以待设计波形x∈N×1为例,需满足目标函数:

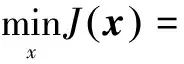
(6)

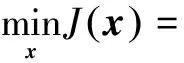
(7)

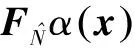
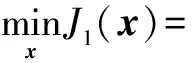
(8)

由文献[1]中“等价性”知,上式优化问题可简化为:

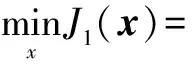
(9)

从而使得抑制强散射体旁瓣遮蔽的波形设计问题转化为待设计波形频谱与理想波形频谱的逼近问题.

其次,为解决MIMO雷达阵元间波形互扰问题构造目标函数,考虑到旁瓣干扰存在于各个延迟时刻,因此由式(3)可得目标函数为:

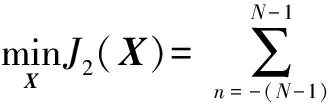
(10)

式中‖·‖F表示矩阵Frobenius范数；利用Parseval定理可知上述目标函数等价为:

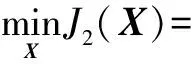
(11)

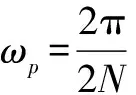
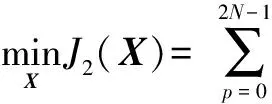
(12)

第三,为抑制特定频带电磁干扰,即考虑稀疏频谱波形设计问题,由式(5)得目标函数形式:

(13)

由上可知,抑制特定频带电磁干扰的波形设计问题转化为发射波形频谱应在该频带区间内具备较低的频谱幅度,从而使得目标函数转化为逼近优化问题.

最后,为充分利用发射机功率即要求发射波形满足恒模约束,从而有:

(14)

以上目标函数和约束可视为波形设计中的各个任务,对于MIMO雷达某任务场景而言,复杂任务可视为包括上述目标函数或约束中的一个或多个.

3.2 波形求解方法

恒模约束往往导致波形设计问题非凸,循环算法或迭代算法因随机初始化而收敛缓慢且难以获得全局解[8,16,17],这使得针对不同任务需求的恒模波形设计问题求解较为困难.由文献[18]知松弛交替投影机制能够加快收敛且具有较好收敛性能.

假定集合A代表恒模约束集合,集合B代表各目标函数集合,构造变量y到集合A的投影ProjA(y)及变量x到集合B的投影ProjB(x),如下:

(15)

(16)

其中,d(i,j)=‖i-j‖表示变量i和j间的距离；那么,交替投影机制简述为:首先选定集合A中某元素x1,求取其到集合B中投影,即选取集合B中元素y1使得y1=ProjB(x1),即d(x1,y1)最小；然后,再以y1为起点,求取其到集合A中投影,即选取集合A中元素x2=ProjA(y1)；这样周而复始实现迭代映射,存在d(xk+1,yk+1)≤d(xk,yk+1)≤d(xk,yk),当d(xk+1,yk+1)足够小时,xk+1或yk+1将可能同时满足集合A、B的特性.但恒模非凸条件下,迭代映射后期收敛缓慢,故引入松弛交替投影框架Tδ(·),λ:A→B→A,如下:

Tδ(·),λx=ProjA(x+λ·δ(x)·(ProjA(ProjB(x))-x))

(17)

式中λ∈(0,1]表示松弛算子；δ(·)表示加速因子,有如下不同形式:

(18)

(19)

通过加速因子和松弛算子,松弛交替投影机制能够利用各次迭代映射投影元之间的关系(如projA(projB(x))-projB(x)和ProjA(ProjB(x))-x分别表示迭代映射投影元间的差值)来对原交替投影问题的解进行松弛和优化,进而对非凸问题求解过程中的局部停滞起到了跳出局部区域的作用.

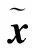
针对抑制特定旁瓣区间强散射体遮蔽干扰的恒模波形设计问题,构造优化问题如下:

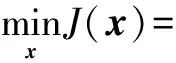
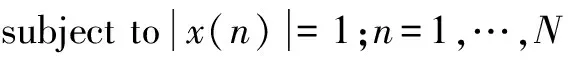
(20)

则相应松弛迭代谱拟合交替投影算法框架见算法1.

算法1 针对抑制特定旁瓣区间强散射体遮蔽干扰的RISAAP算法

步骤1 随机初始化:x(k)∈N×1；

步骤2 基于当前迭代解x(k)利用以下公式获得后续迭代解x(k+1):

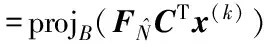
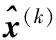
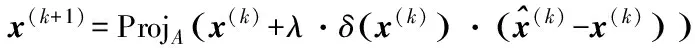
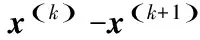
步骤4 重复步骤2和步骤3,直到循环迭代达到总数K或满足算法迭代误差阈值ε；

针对抑制MIMO雷达阵元间波形互扰的恒模波形设计问题,构造此任务场景下的优化问题如下:

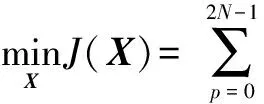
(21)

则相应松弛迭代谱拟合交替投影算法框架见算法2.

算法2 针对抑制阵元间波形互扰的MDRISAAP(Multi-Dimensional RISAAP)算法

步骤1 随机初始化:

X(1)=[x1x2…xM]∈N×M；

步骤2 基于当前迭代解X(k)利用以下公式获得后续迭代解X(k+1):

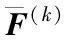
其中矩阵D∈2N×M中各元素；

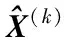
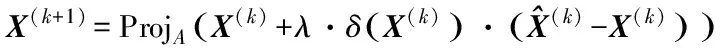
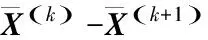
步骤5 重复步骤2、3和4,直到循环迭代达到总数K或满足算法迭代误差阈值ε；

针对联合抑制特定频带电磁干扰和距离旁瓣干扰的恒模波形设计问题,在此引入权值联合多目标优化RISAAP算法,权值通常取γ∈(0,1),如下所示:

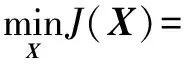
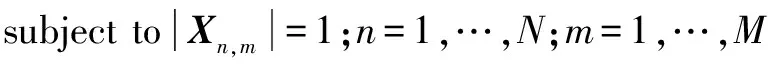
(22)

则相应松弛迭代谱拟合交替投影算法框架见算法3.

算法3 针对联合抑制特定频带电磁干扰及相关旁瓣干扰的MDRISAAP算法

步骤1 随机初始化:X(1)=[x1x2…xM]∈N×M；

步骤2 基于当前迭代解X(k)利用以下公式获得后续迭代解X(k+1):

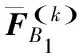
其中矩阵D∈2N×M中各元素；

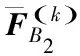
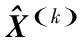
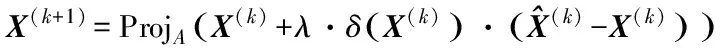
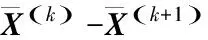
步骤5 重复步骤2、3和4,直到循环迭代达到总数K或满足算法迭代误差阈值ε；

4 实验仿真

本节就上述三个波形设计任务场景,将所提算法与当前流行算法比较,仿真平台为i7-4770 CPU 3.40GHz,Matlab R2014a,64位.

4.1 抑制特定旁瓣区间强散射体遮蔽干扰的波形设计

假定单旁瓣干扰区间Qr1=[1:30]及多旁瓣干扰区间Qr2=[20:30]∪[40:60],波形序列码长为150；将算法1中RISAAP与文献[8]中WeCAN、文献[12]中ISAA及梯度算法PONLP(ISAA)比较,算法迭代终止条件为K=1000或ε=10-13.另定义自相关幅值电平(ACL,Autocorrelation Level),如下:

(23)

本节采用100次独立重复试验来统计分析算法性能:定义平均耗时及抑制区间内平均自相关幅值电平为:Aver-time(s)和 Aver-ACL(dB).不同算法抑制特定旁瓣区间干扰性能比较如表1、图1所示:

表1 不同算法抑制特定旁瓣区间干扰性能比较

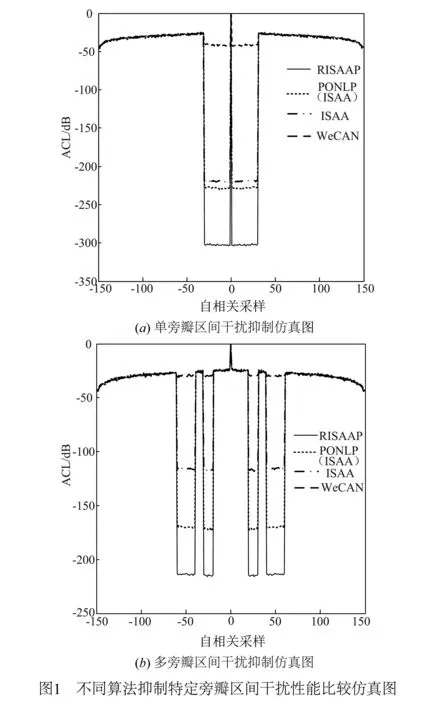
从表1知:对于单、多旁瓣区间干扰抑制,RISAAP在耗时和Aver-ACL方面都获得了比ISAA、PONLP(ISAA)和WeCAN较佳的性能优势.从表1中单旁瓣区间抑制可知,RISAAP耗时仅为WeCAN的约2.3 %,Aver-ACL相较WeCAN提升约261dB；RISAAP相较ISAA耗时优势不明显,但Aver-ACL提升约84dB；PONLP(ISAA)首先利用ISAA获得初始解,然后利用梯度算法迭代优化,其耗时为ISAA的约2倍且获得约9dB提升.同样由多旁瓣区间抑制可得:RISAAP耗时仅为WeCAN的约4%,Aver-ACL相较WeCAN提升约185dB；RISAAP与ISAA相比耗时不明显,但RISAAP所得Aver-ACL提升约100dB；PONLP(ISAA)耗时为ISAA的约1.8倍且Aver-ACL改善约56dB.对于恒模约束下的非凸问题,ISAA、WeCAN在迭代优化后期收敛缓慢而陷入局部最优；PONLP(ISAA)依靠ISAA和梯度算法迭代优化,仍然难以避免局部停滞；而RISAAP算法凭借松弛算子和加速因子能够摆脱局部收敛束缚,逼近全局最优.本节采用100次独立重复试验并取统计平均结果分析,而非仅取最优结果表示,从图1可看出所提算法的稳定性.

4.2 降低阵元间波形互扰的波形设计

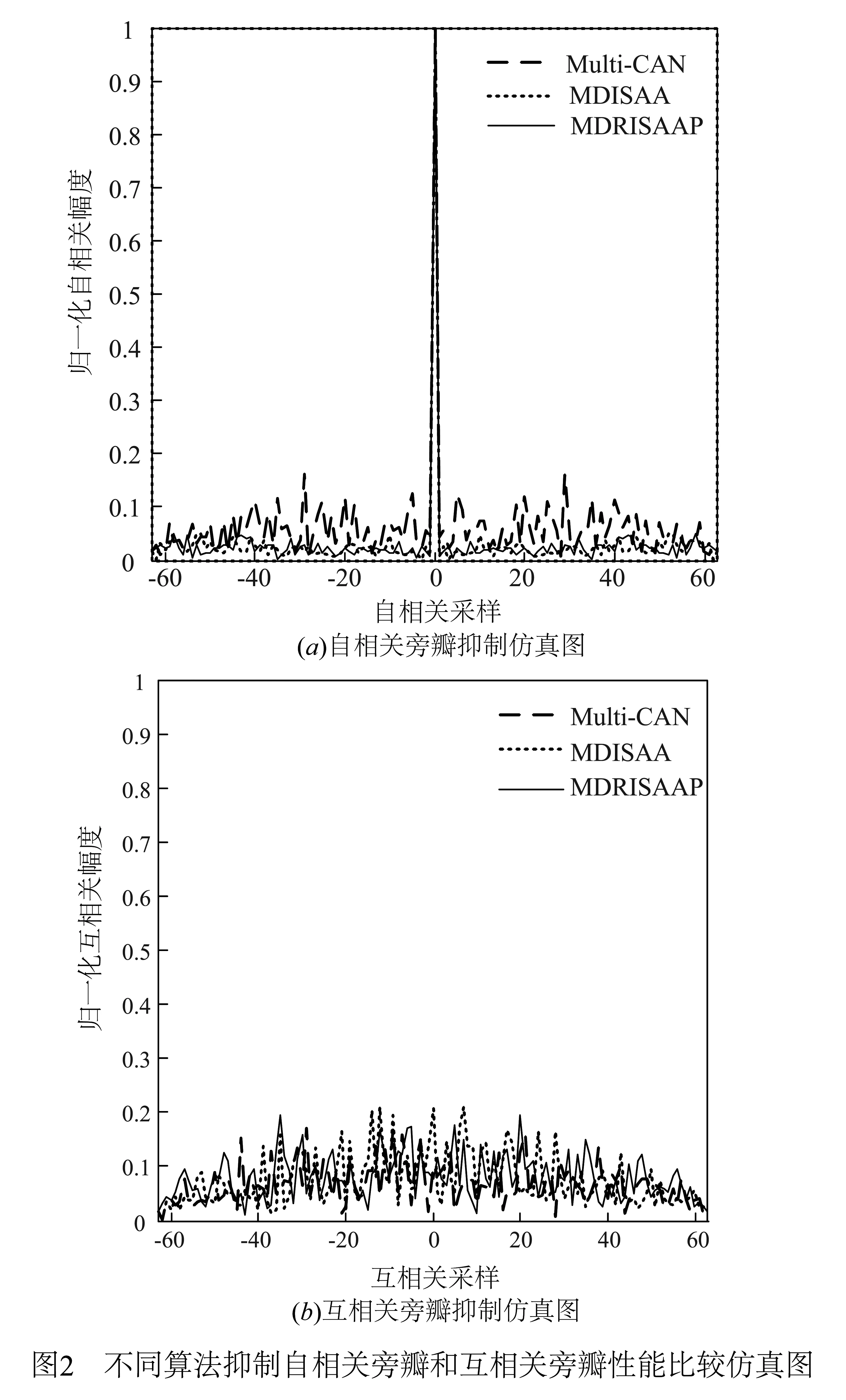
假定MIMO雷达具有3个发射阵元,且各阵元波形序列码长均为64,将算法2中MDRISAAP与文献[8]中Multi-CAN、文献[10]中MDISAA比较,算法迭代终止条件为K=10000或ε=10-4.以第1个阵元为例作不同算法优化波形自相关、互相关幅度(第1、3阵元波形互相关)性能比较,见图2.

另外,分别以各阵元波形序列码长40、64、128、256、512、1024为例,采用100次独立重复试验来比较Multi-CAN、MDISAA 、MDRISAAP耗时性能,得到针对不同序列长度各算法进行100次试验总耗时比较如表2所示:

表2 不同序列长度各算法耗时比较

由图2知:MDRISAAP和MDISAA相较Multi-CAN获得了更低的自相关旁瓣幅度,而对于互相关幅度三种算法差异并不明显；由表2知:对于同一长度序列(以码长40为例)MDRISAAP耗时2.05s明显少于Multi-CAN和MDISAA,体现了低耗时性能；随波形序列码长增大,MDRISAAP与MDISAA、Multi-CAN差异愈见突出(当码长为1024时,MDRISAAP耗时仅为MDISAA的约16.5%、Multi-CAN的约10%).这是由于松弛交替投影机制在大长度序列迭代优化过程中将多维问题进行松弛转换,从而使得计算复杂度呈现较低的一种趋势,这也说明所提RISAAP框架更适合波形在线设计.

4.3 联合抑制特定频带电磁干扰及相关旁瓣干扰的波形设计

假定MIMO雷达有3个发射阵元,各阵元波形时宽为704μs,采样频率为710KHz,则各阵元波形序列码长为500.假设电磁干扰分散存在于频带[160,180]∪[200,260]∪[280,350]∪[370,400]∪[420,450]kHz中,则其通带处于[0,710]kHz中剩余部分.将算法3中MDRISAAP与文献[11]中MDISAA及文献[16]中CIA比较,各算法均采用相同随机初始化方式,且设定算法终止条件为K=1000或ε=10-4,联合优化权值γ=0.45；另定义自相关旁瓣峰值(ASP,Autocorrelation Sidelobe Peak)、阻带功率峰值(PSP,Peak Stopband Power)及互相关旁瓣峰值(CSP,Crosscorrelation Sidelobe Peak)如下:

(24)

(25)

上式中PSDstop表示特定频带区间中功率谱密度值.

n=1,2,…,N-1;m1≠m2

(26)

cn(xm1,xm2)表示在第n个采样延时两阵元发射波形间的互相关.利用算法所得各阵元波形的ASP、PSP、CSP性能指标取均值,得到CIA、MDISAA及MDRISAAP性能比较如表3所示；选取第一个阵元为例作自相关、互相关幅度(第1、2阵元波形互相关)及特定频带干扰抑制性能比较如图3所示.

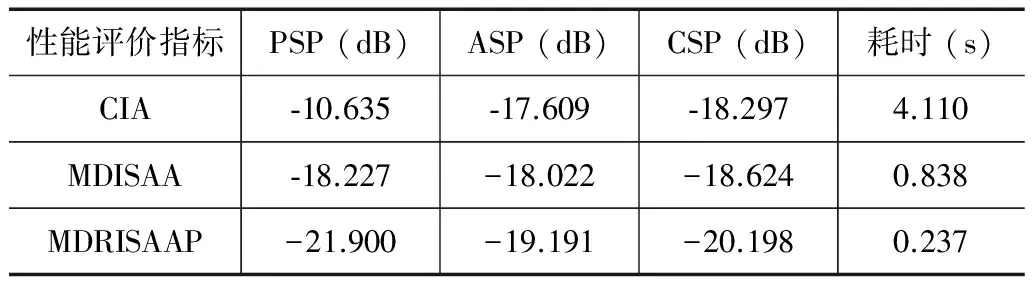
由表3知:对于联合抑制特定频带电磁干扰和相关旁瓣干扰的多目标联合优化波形设计问题,CIA耗时较长(4.110s),分别是MDISAA和MDRISAAP的约5倍和约17倍,且在PSP指标下差于MDISAA和MDRISAAP,而其ASP、CSP指标与MDISAA和MDRISAAP相差不大；当阵元数目较多或波形序列长度较大时将可能增加CIA计算复杂度,且易陷入局部停滞而导致收敛缓慢、耗时较长.MDRISAAP在PSP、ASP、CSP性能评价方面均略优于MDISAA,这是由于MDRISAAP凭借其加速因子和松弛算子能够优化局部弱收敛区,耗时仅为MDISAA的约28.3%.从图3(a)和3(b)可知三种算法对于抑制旁瓣干扰性能差异不明显,但从图3(c)可看出,MDRISAAP和MDISAA相比CIA获得了更低的抑制幅度,这与表3数据一致.

表3 不同算法针对联合抑制特定频带干扰及相关旁瓣干扰性能比较

性能评价指标PSP(dB)ASP(dB)CSP(dB)耗时(s)CIA⁃10．635⁃17．609⁃18．2974．110MDISAA⁃18．227-18．022-18．6240．838MDRISAAP-21．900-19．191-20．1980．237

5 结论

实验仿真表明,针对恒模、强散射体遮蔽干扰、阵元间波形互扰及特定频带电磁干扰等复杂任务场景,所提算法运算效率高、可有效避免局部停滞且具有较高鲁棒性,与当前流行算法相比更适合在线波形设计；这与松弛迭代谱拟合交替投影的机制密切相关.但如何妥善联系各个任务以满足尽可能多的设计要求,这将成为下一个研究重点；对于复杂任务场景而言,增多子任务意味着问题求解复杂度可能成倍增加,这都极其考验算法稳定性和实时性.

[1]He H,Stoica P,Li J.Designing unimodular sequence sets with good correlations—Including an application to MIMO radar [J].IEEE Transactions on Signal Processing,2009,57(11):4391-4405.

[2]蒋敏,黄建国,韩晶.MIMO阵列恒定包络波形设计 [J].电子学报,2011,39(9):2194-2199. Jiang Min,Huang Jian-guo,Han Jing.Constant envelope waveform design for MIMO array [J].Acta Electronica Sinica,2011,39( 9):2194-2199.( in Chinese)

[3]陈浩文,黎湘,庄钊文.一种新兴的雷达体制—MIMO雷达[J].电子学报,2012,40(6):1190-1198. Chen Hao-wen,Li Xiang,Zhuang Zhao-wen.A rising radar system-MIMO radar [J].Acta Electronica Sinica,2012,40(6):1190-1198.(in Chinese)

[4]赵伟,赵永波,李慧,等.MIMO雷达正交频分非线性调频波形设计 [J].电子学报,2014,42(11):2331-2336. Zhao Wei,Zhao Yong-bo,Li Hui,et al.Orthogonal frequency division-nonlinear frequency modulation waveform design for MIMO radar [J].Acta Electronica Sinica,2014,42(11):2331-2336.(in Chinese)

[5]Cheng S,Wang W Q,So H C.MIMO radar OFDM chirp waveform diversity design with sparse modeling and joint optimization [J].Multidimensional Systems and Signal Processing,2015:1-13.

[6]Wang G,Lu Y.Clutter rank of STAP in MIMO radar with waveform diversity [J].IEEE Transactions on Signal Processing,2010,58(2):938-943.

[7]唐波,张玉,李科,等.杂波中MIMO雷达恒模波形及接收机联合优化算法研究[J].电子学报,2014,42(9):1705-1711. Tang Bo,Zhang Yu,Li Ke,et al.Joint constant-envelope waveform and receiver design for MIMO radar in the presence of clutter [J].Acta Electronica Sinica,2014,42(9):1705-1711.(in Chinese)

[8]He H,Li J,Stoica P.Waveform Design for Active Sensing Systems:A Computational Approach [M].Cambridge:Cambridge University Press,2012.17-147.

[9]Wu H,Song Z,Fan H,et al.A new algorithm for sparse frequency waveform design with range sidelobes constraint [J].Chinese Journal of Electronics,2015,24(3):604-610.

[10]赵宜楠,张涛,李风从,等.基于交替投影的MIMO雷达最优波形设计[J].电子与信息学报,2014,36(6):1368-1373. Zhao Yi-nan,Zhang Tao,Li Feng-cong,et al.Optimal waveform design for MIMO radar via alternating projection [J].Journal of Electronics & Information Technology,2014,36(6):1368-1373.(in Chinese)

[11]Zhao Y N,Li F C,Zhang T,et al.Computational design of optimal waveforms for MIMO radar via multi-dimensional iterative spectral approximation [J].Multi-dimensional Systems and Signal Processing,2016,27(1):43-60.

[12]Li F C,Zhao Y N,Qiao X L.A waveform design method for suppressing range sidelobes in desired intervals [J].Signal Processing,2014,96(3):203-211.

[13]王旭,周生华,刘宏伟,等.一种空时联合优化的MIMO雷达波形设计方法 [J].西安电子科技大学学报,2014,41(3):41-48. Wang Xu,Zhou Sheng-hua,Liu Hong-wei,et al.Waveform design method for MIMO radar based on joint spatial and temporal optimization [J].Journal of Xidian University,2014,41(3):41-48.(in Chinese)

[14]Liu B,He Z.Orthogonal discrete frequency-coding waveform design for MIMO radar [J].Journal of Electronics (China),2008,25(4):471-476.

[15]Zhao Z S,Feng X,Lin Y,et al.Evolved neural network ensemble by multiple heterogeneous swarm intelligence [J].Neurocomputing,2015,149(2):29-38.

[16]庄珊娜,贺亚鹏,朱晓华.低距离旁瓣稀疏频谱波形相位编码设计 [J].电子与信息学报,2012,34(5):1088-1095. Zhuang Shan-na,He Ya-peng,Zhu Xiao-hua.Phase coding for sparse frequency waveform with low range sidelobes [J].Journal of Electronics & Information Technology,2012,34(5):1088-1095.(in Chinese)

[17]Patton L K,Rigling B D.Phase retrieval for radar waveform optimization [J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(4):3287-3302.

[18]Cegielski A,Suchocka A.Relaxed alternating projection methods [J].SIAM Journal on Optimization,2008,19(3):1093-1106.

冯 翔 男,1988年1月出生,山东潍坊人.现为哈尔滨工业大学电子与信息工程学院博士研究生.主要研究方向为认知雷达、雷达自适应信号处理、机器学习等.

E-mail:fengxiang230316@163.com

陈志坤 男,1982年7月出生,福建漳州人,现为哈尔滨工业大学博士研究生,主要研究方向为雷达信号处理、电子侦察技术.

E-mail:chih-quinn-chen@yeah.net

李风从 男,1985年12月出生,湖北黄石人.博士,现为湖北工业大学讲师.主要研究方向为自适应信号处理.

E-mail:xialulee@sina.com

赵宜楠(通信作者) 男,1977年2月出生,黑龙江哈尔滨人.现为哈尔滨工业大学(威海)信息工程研究所教授、博士生导师.主要研究方向为新体制雷达、自适应信号处理.

E-mail:hrbzyn@163.com

Phase-Coded Waveform Design via Relaxed Alternating Projection for MIMO Radar

FENG Xiang,CHEN Zhi-kun,LI Feng-cong,ZHAO Yi-nan

(SchoolofElectronicsandInformationEngineering,HarbinInstituteofTechnology,Harbin,Heilongjiang150001,China)

The sophisticated scenarios always challenge MIMO(Mutiple-Input Mlitiple-Output) radar.A relaxed iterative spectrum approximation alternating projection method (RISAAP) is proposed to design phase-coded waveforms,for suppressing high range sidelobes of strong scatters,electromagnetic interference in specified frequencies and cross-interference from different signals.This method is based on power spectral density (PSD) approximation and alternating projection with extended accelerating factor.Firstly,the correlation fitting is transformed into PSD approximation via FFT between the aperiodic correlation function and PSD.Secondly,the desired spectrum constraint is formulated and the projection space is expanded by its relaxed mechanism.Finally,the iterative optimization is conducted via FFT and accelerated alternating projection.Simulations demonstrate that this method could obtain efficient performance and avoid local stagnation which seems more convenient for waveform design on-the-fly than some prevalent algorithms.

MIMO radar; waveform design; power spectral density approximation; phase-coded; alternating projection

2015-03-30；

2016-2-25;责任编辑：梅志强

国家自然科学基金(No. 61371181 )

TN957.51

A

0372-2112 (2016)12-2981-08

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.12.024