单目图像序列光流三维重建技术研究综述

张聪炫，陈 震，黎 明

(1.南昌航空大学无损检测技术教育部重点实验室,江西南昌 330063;2.南昌航空大学测试与光电工程学院,江西南昌 330063)

单目图像序列光流三维重建技术研究综述

张聪炫1,2，陈 震1,2，黎 明1

(1.南昌航空大学无损检测技术教育部重点实验室,江西南昌 330063;2.南昌航空大学测试与光电工程学院,江西南昌 330063)

由单目图像序列光流重建物体或场景的三维运动与结构是计算机视觉、图像处理与模式识别等领域的重要研究内容，在机器人视觉、无人机导航、车辆辅助驾驶以及医学影像分析等方面具有重要的应用.本文首先从精度与鲁棒性等方面对单目图像序列光流计算及三维重建技术近年来取得的进展进行综述与分析.然后采用Middlebury测试图像序列对HS、LDOF、CLG-TV、SOF、AOFSCNN和Classic+NL等典型光流算法以及Adiv、RMROF、Sekkati和DMDPOF等基于光流的间接与直接重建方法进行实验对比分析，指出各对比方法的优点与不足，归纳各类方法的性能特点与适用范围.最后对利用分数阶微分模型、非局部约束、立体视觉以及深度线索解决亮度突变、非刚性运动、运动遮挡与模糊情况下光流计算及重建模型的局限性与鲁棒性问题进行总结与展望.

单目图像序列；光流；运动估计；三维重建；困难场景；鲁棒性

1 引言

光流是指运动物体或场景表面的光学特征部位在投影平面的瞬时速度，其不仅包含了物体或场景的运动参数，还携带了丰富的三维结构信息.研究基于单目图像序列光流的三维重建技术就是研究如何利用图像光流估计目标运动物体或场景的三维运动速度并重建其三维结构.21世纪以来，随着图像传感器以及电子芯片技术的飞跃式发展，基于单目图像序列光流的三维重建技术已在航空航天、军事、工业、医疗等领域显示出越来越重要的地位与作用，例如应用于工业机器人的视觉系统[1]、车辆行进过程中的前景及障碍物检测[2]、红外图像中运动目标的检测与跟踪[3]、无人机导航与起降系统[4]、卫星云图分析与三维显示[5]、医学图像器官的三维重建与分析、诊断[6]等等.

根据计算策略的不同，基于单目图像序列光流的三维重建方法大致可以分为两类：基于稠密光流的方法和基于稀疏光流(特征光流)的方法.基于稠密光流的三维重建技术是利用运动物体或场景表面稠密像素点的图像运动估计其对应的三维运动与深度信息，因此该类方法可以较好地描述运动物体或场景的表面细节信息.根据研究阶段的不同，基于稠密光流的三维重建技术主要分为图像序列光流计算技术研究和基于稠密光流的三维重建技术研究.其中，图像序列光流计算技术是基于稠密光流三维重建技术的重要基础，光流计算的精度直接关系三维运动估计与结构重建的效果.基于稀疏光流的三维重建技术需要首先提取图像序列中运动物体或场景表面的图像特征(例如图像中的角点、直线、曲线等特征)，然后对提取的特征跟踪、匹配并计算出其对应的图像坐标变化，从而根据特征光流与三维运动和空间结构的投影关系重建三维运动与结构.由于只是采用图像序列中感兴趣的图像特征对物体或场景进行描述，基于稀疏光流的三维重建技术能够克服亮度突变现象对重建结果的影响.

根据单目图像序列光流三维重建技术的分类以及研究阶段的不同，本文分别从图像序列光流计算技术、基于稠密光流的三维重建技术和基于稀疏光流的三维重建技术等方面对单目图像序列光流三维重建理论与方法的研究现状以及现存的关键问题与后期研究方向进行扼要的介绍及分析.

2 图像序列光流计算技术

1981年，Horn和Schunck[7]通过对光流基本约束方程添加平滑项构成全局能量函数，开创性地提出了光流估计模型：

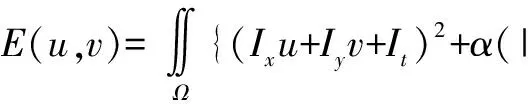
(1)式中，Ω表示图像区域，I(x,y)表示图像像素点(x,y)T处的灰度值，(Ix,Iy,It)T表示图像灰度沿x、y轴以及时间t方向的偏导.=(∂x∂y)T表示梯度算子，α是平滑项权重系数.对式(1)中光流分量u、v分别求导后可以推导出对应的迭代公式进而计算光流矢量w=(u,v)T.Lucas和Kanade[8]假设在图像中一个较小区域内各像素点的光流值相等，利用加权函数对各像素点进行约束，提出了局部光流算法，该方法充分考虑图像像素点的局部邻域信息，有效地提高光流计算模型的抗噪性，但由于采用邻域光流一致的计算策略，导致光流结果并不是完全稠密的[9].

在光流计算模型中，数据项主要由基于图像数据的守恒假设构成，是决定光流计算精度与鲁棒性的主要因素.针对基本约束方程在图像中包含光照变化时可靠性较差的问题，基于图像梯度[10]、图像结构张量[11]等数据的高阶守恒假设逐渐成为数据项的重要组成部分.Papenberg[12]等人对不同类型守恒假设进行理论分析和实验对比，证明了灰度守恒假设与梯度守恒假设的联合形式总体性能较优.针对光照阴影对光流计算的影响，基于图像纹理、结构分解的图像数据处理方法能够有效地降低图像阴影区域对守恒假设造成的误差[13].鉴于传统数据项采用的平方模型易导致守恒假设误差的非线性增大，基于Charbonnier函数的非平方模型成为现阶段解决光流计算鲁棒性的有效手段[14].针对光流模型的抗噪性能，Drulea[15]在数据项采用全局优化与局部优化相结合的方法，既提高了光流计算的抗噪性，又能得到稠密的光流场.鉴于彩色图像能够提供更多的图像信息，项学智[16]提出了基于多通道和色彩梯度守恒的光流计算模型，进一步提高了数据项模型的准确性与可靠性.

光流计算模型的平滑项主要由各种平滑策略构成，决定了光流扩散的方向和程度.由于传统的一致扩散策略造成图像边缘过于平滑，基于图像梯度的自适应变化扩散策略最早被用于解决图像边缘区域光流过度发散的问题[17].针对各向同性扩散易导致图像边缘模糊的问题，Werlberger[18]提出基于图像结构张量的各向异性扩散策略，通过控制光流在图像边缘不同方向的扩散程度克服由于光流扩散所导致的边缘模糊现象.由于图像边缘与运动边缘并不一定完全重合，基于光流驱动的平滑项扩散策略[19]能够降低图像中运动边缘处溢出点对光流计算的影响，使得光流结果充分体现了运动细节.针对图像驱动与光流驱动两类平滑项扩散策略各自的优缺点，Zimmer[20]提出基于图像与光流联合驱动的平滑项模型，使得光流估计结果既能体现运动细节又尽可能地贴合图像边缘.

近年来，随着图像计算难度的增大，光流模型的计算策略及优化方法研究逐渐成为热点问题.针对大位移光流估计问题，Brox[21]通过将金字塔变形分层策略与区域匹配方法相结合，有效提高了大位移运动光流计算的精度与鲁棒性.当图像序列中存在运动遮挡情况时，光流估计在遮挡区域常常包含较大误差，Ayvaci[22]在朗伯反射与光照不变的条件下提出面向稀疏遮挡的光流计算方法，部分解决了遮挡区域光流计算的可靠性问题.针对光流计算的鲁棒性与时效性问题，Zhang[23]采用双层细胞神经网络对基于多守恒假设与各向异性扩散相结合的光流模型进行优化，提高了光流计算的精度与时效性.针对困难场景光流计算的准确性问题，Sun[24]通过在金字塔分层迭代时对图像光流进行加权中值滤波优化，大幅提高了光流估计的精度与鲁棒性.Middlebury学院的计算机视觉研究中心对不同光流算法进行了系统的比较与分析，提出了Middlebury评价标准[25]，并提供了不同类型的测试图像序列，为光流计算的后续研究奠定了基础.

针对图像序列光流计算策略的对比问题，本文分别选取HS[7]、LDOF[21]、CLG-TV[15]、SOF[22]、AOFSCNN[23]以及Classic+NL[24]等代表性方法进行光流计算评测.测试图像采用图1所示的Middlebury数据库提供的Dimetrodon、Grove3、Rubberwhale以及Urban2图像序列.其中，Dimetrodon图像序列包含非刚性复杂运动、Grove3图像序列包含复杂边缘结构与运动间断、RubberWhale图像序列包含多目标复杂运动以及阴影区域、Urban2图像序列同时存在运动遮挡与小位移光流.图2展示了各对比方法计算所得光流结果，由于HS算法是光流计算的起源方法，针对本实验所采用的图像序列，HS算法计算效果最差，说明HS算法已无法满足复杂困难场景图像序列光流计算的要求.LDOF算法针对Urban2图像序列光流计算效果较差，说明该方法不适用于运动遮挡与小位移光流类型图像；CLG-TV算法针对Grove3与Rubberwhale图像序列光流计算效果较差，主要源于该方法采用局部与全局优化相结合导致光流计算在图像边缘细节区域过于平滑；SOF算法针对Rubberwhale与Urban2等包含遮挡与阴影的图像序列计算效果较好，但针对Grove3等包含复杂边缘轮廓的图像序列光流计算效果不理想；AOFSCNN算法与Classic+NL算法光流计算整体效果较好，说明这两种方法针对非刚性运动、复杂边缘、运动遮挡以及小位移光流等困难场景具有较好的适用性.

表1分别给出了各对比方法光流计算结果的平均角误差(Average Angle Error，AAE)与平均端点误差(Average Endpoint Error，AEE)，其中，AAE误差指标反映的是光流计算结果的平均相对角误差，即光流整体偏移程度；AEE误差指标反映的是光流计算结果的平均端点误差，即光流平均绝对误差.由表1可以看出，Classic+NL算法在Grove3、Rubberwhale以及Urban2等三组图像序列中AAE误差最小，说明Classic+NL算法光流计算结果整体偏移程度较小；AOFSCNN算法针对Grove3与Urban2等两组图像序列AEE误差指标表现最优，说明AOFSCNN算法光流计算绝对误差较小.

表1 Middlebury测试库图像序列光流计算误差对比

3 基于稀疏光流的三维重建技术

3.1 基于稀疏点光流的三维重建技术

基于图像序列稀疏光流的三维重建研究始于20世纪80年代，Roach[26]首先根据图像特征点与三维空间点的几何对应关系提出了基于图像稀疏点光流的非线性三维重建算法.针对非线性算法无法获得唯一解的问题，Zhuang和Huang[27]提出基于特征点光流的三维重建线性算法.由于线性算法重建模型对图像噪声较为敏感，以扩展卡尔曼滤波为代表的各类数字率滤波器在20世纪末被广泛用于稀疏点光流三维重建模型的优化[28]，但由于该类方法通常需要长序列图像进行状态估计，导致其重建模型的时间消耗过大.

随着图像特征点提取技术的快速发展，基于稀疏点光流的三维重建技术在重建精度等方面得到较大提高.针对多运动目标的三维重建问题，Ozden[29]采用概率统计对匹配得到的稀疏点光流进行分类，提高了多目标三维重建的可靠性.王俊[30]提出一种基于图像匹配-特征点云融合的三维重建方法，通过匹配不同点云模型在同一幅图像上的投影点确定特征光流对应集，提高了大场景三维重建的精度.针对复杂运动物体和场景的三维重建问题，Nachimson[31]通过分解旋转和平移运动提出基于二次全局优化的特征点光流三维重建方法,提高了复杂运动三维重建的精度.

近年来，随着鲁棒估计算法在计算机视觉领域的广泛应用，稀疏点光流三维重建技术的鲁棒性得到较大提高.针对场景与摄像机相对运动情况下的三维重建问题，Scaramuzza[32]提出基于RANSAC约束的稀疏点光流鲁棒重建模型，并将其应用于车载摄像头的场景重建，展现了该类方法的应用价值.针对室外大场景的三维重建问题，Crandall[33]利用离散马尔科夫随机场与连续Levenberg-Marquardt算法构造稀疏点光流三维重建模型，提高了复杂环境下三维重建模型的鲁棒性.针对运动遮挡等困难类型图像序列，Sinha[34]通过非线性插值对图像序列中的点和消失点进行匹配，提出基于多级优化的线性稀疏点光流三维重建模型，部分解决了遮挡、形变等情况下三维重建的可靠性问题.

3.2 基于稀疏直线光流的三维重建技术

鉴于基于稀疏点光流的三维重建技术仅仅利用图像中像素点这一最小单位，当图像序列中存在大位移运动、运动遮挡与模糊等困难运动类型时，稀疏点光流重建模型的鲁棒性问题仍未得到较好地解决.直线是计算机视觉中最常用的一种特征信息，相对于单个像素点，直线特征的抽象层次更高，能够提供更多的拓扑结构信息.因此，基于直线光流的三维重建方法逐渐成为稀疏光流重建技术的研究热点.

1988年，Liu和Huang[35]首先提出利用三帧图像直线光流计算运动物体旋转和平移运动的非线性重建模型.由于非线性算法不能保证运动估计的唯一解，Liu和Huang[36]又提出基于直线光流的三维运动估计线性模型.陈震[37]首次定义了直线光流的概念，并提出基于直线光流的刚体运动估计与结构重建线性模型.针对重建算法的鲁棒性问题，文献[38]和[39]分别利用误差函数和全局优化建立直线光流三维重建非线性模型，抑制了图像噪声对直线重建精度的影响.

针对某些场景可供利用直线光流数量较少的问题，文献[40]提出了基于最优数量直线光流的三维重建线性模型，但由于模型的鲁棒性与直线数量相关，当直线数量较少时，重建精度较差.Mosaddegh[41]利用直线光度守恒假设对三维重建模型进行约束，提高了直线光流数量较少时重建算法的精度.针对不规则运动物体或场景的三维重建问题，Liu[42]以多条直线段拟合曲线特征，提出适用于复杂表面刚体的直线光流重建模型.Elqursh[43]提出基于正交直线光流的运动估计模型，降低了重建模型对图像帧数的要求.

4 基于稠密光流的三维重建技术

4.1 间接重建方法

基于稠密光流的间接重建方法是通过图像光流与三维运动的空间几何关系重建运动物体或场景三维运动与结构.1983年，Bruss[44]首先提出基于局部区域光流的三维运动估计模型，虽然模型简单、重建效率较快，但由于缺少对光流误差的惩罚导致重建效果较差.当图像序列光流估计结果包含较大误差时，如何减小光流误差对重建模型的影响至关重要.Kolev[45]根据最大流-最小割原理提出基于全局约束与局部约束相结合的重建模型，有效地抑制了光流误差的负面影响.针对局部区域内光流误差的相互传导问题，文献[46]提出基于正定矩阵的稠密光流间接重建模型，通过切断光流误差的传递路径保证了重建模型的鲁棒性.针对真实场景的三维重建问题，Chessa[47]采用可调节参数滤波对线性重建模型进行优化，既提高了重建结果的准确性，又能够缩减时间消耗.

当图像序列中包含多个运动物体时，如何准确区分不同物体的运动区域是间接重建方法的一个关键问题.Adiv[48]首先根据光流估计结果对运动目标进行动态阈值分割，再利用加权局部区域算法计算运动物体的三维运动参数和相对深度信息，但由于光流区域常常大于运动物体的真实区域，因此重建结果并不理想.针对阈值分割的缺点，Meinhardt[49]使用边缘检测算子对图像光流进行分割，并利用运动物体的边缘约束条件重建其相对深度.针对遮挡情况下间接重建模型的准确性与可靠性问题，Calway[50]提出基于改进卡尔曼滤波的递归重建模型，通过采用长序列图像修正策略使得重建模型具有较好的鲁棒性.针对长序列导致时间消耗过大的问题，Lee[51]提出基于图像光流的概率统计的三维重建模型，既提高了运动物体遮挡情况下重建模型的准确性，又减小了重建模型的时间消耗.4.2 直接重建方法

鉴于光流计算过程常常会给间接重建算法带来较大的时间消耗与计算误差，Horn和Weldon[52]通过图像像素点亮度与对应空间点的透视投影关系首先定义基于亮度恒等的三维运动估计守恒假设，然后提出基于局部邻域约束的稠密光流三维重建直接方法.基于稠密光流的直接重建方法无须事先计算图像光流，有效地降低了光流计算所带来的误差风险与时间消耗，因此迅速成为单目图像光流三维重建技术研究的热点.

针对直接重建方法的精度问题，Mitiche[53]提出基于最小描述长度原理约束的三维重建模型，但该方法只适合估计平移运动参数.Sekkati[54]通过引入正则化因子，构建基于全局优化的直接重建模型，解决了直接重建方法的局部最优解问题.针对非刚性运动的重建问题，Perriollat[55]使用距离守恒假设对重建模型进行约束，并采用时空滤波对运动估计优化，提高了非刚性运动情况下重建模型的可靠性.针对多目标三维重建问题，Mitiche[56]在重建模型中利用水平集演化搜索运动物体或场景的边缘轮廓，准确地对图像中不同物体或场景进行分割.

针对光照变化情况下重建模型的鲁棒性问题，Zhang[57]提出基于多守恒假设与非线性扩散相结合的直接重建模型，并对特殊运动形式的三维重建问题进行分析，拓展了直接重建方法的适用范围.Ummenhofer[58]提出基于移动背景消除的三维重建模型，能够有效地减小移动背景和物体阴影区域对重建结果的影响.针对大位移运动时重建模型的可靠性问题，文献[59]提出基于图像金字塔分层的全局优化直接重建方法，有效地克服了大位移运动所导致的边缘溢出点问题.Cubber[60]将单目光流重建模型与双目视觉相结合，利用极线约束估计物体或场景的绝对深度，为光流三维重建技术研究开辟了新方向.

为了验证间接重建方法与直接重建方法的性能与特点，分别选取Adiv[48]、RMROF[46]、Sekkati[54]和DMDPOF[59]等重建方法进行对比测试与分析.其中，Adiv与RMROF算法采用AOFSCNN算法[23]作为重建模型的光流计算方法.测试图像选取图3(a)所示的Yosemite图像序列，图中既存在乌云区域的非刚性运动，又包含了山谷的大场景扩张运动，因此具有较高的挑战性.由于Yosemite图像序列没有深度真实值，计算出各对比方法的深度重建结果后使用灰度图表示如图3(e)～(h)所示.图中颜色较深的像素点表示其深度坐标较小，即该点距离摄相机镜头较近；颜色较浅的像素点表示其深度坐标较大，即距离摄相机镜头较远.图3中，Adiv算法重建效果较差，主要源于该方法仅采用局部邻域约束估计三维运动与深度信息，导致其对困难场景的重建效果较差.Sekkati算法重建效果略好于Adiv算法，但由于采用非线性一致扩散策略导致其重建结果过于平滑.RMROF算法与DMDPOF算法重建结果未出现明显的过度分割与不连续现象，整体重建效果较好.

图3(b)～(d)分别展示了光流真实值、AOFSCNN与DMDPOF算法的光流估计结果，图中AOFSCNN算法在乌云区域存在轻微的过度分割现象，而DMDPOF算法则更加平滑，未出现过度分割现象.表2展示了各对比方法的光流误差AAE与AEE统计结果，其中Adiv与RMROF算法采用的是AOFSCNN算法的光流计算结果.表中AOFSCNN算法的AAE误差最小，而DMDPOF算法的AEE误差最小.通过各对比方法的定性分析与定量比较可以看出，精确的光流输入并不一定能保证间接重建方法取得令人满意的重建效果，主要源于不适当的间接重建模型可能会将光流误差放大.直接重建方法计算出的光流结果与重建效果是密切相关的，因此直接重建方法计算出的光流精度越高，说明其重建效果越好.

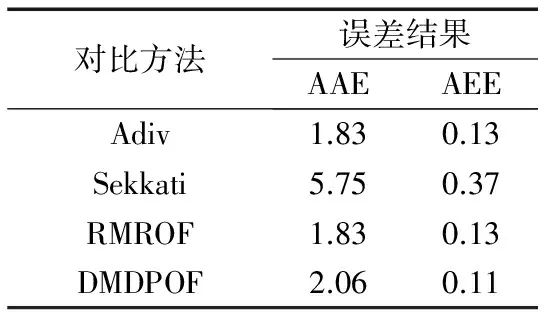
表2 各对比重建方法光流误差结果

5 总结与展望

本文通过对图像序列光流计算技术、基于图像特征光流的三维重建技术以及基于稠密光流的三维重建技术等研究内容进行分类归纳，总结分析了单目图像序列光流三维重建技术的研究热点及重要研究成果，并对光流计算及其三维重建技术研究领域中几类代表性方法进行了实验对比测试，以说明各类方法的性能特点以及适用范围.

虽然单目图像序列光流三维重建技术研究取得了较大进展与诸多成果，但仍有许多相关工作有待进一步深入研究，例如：

(1)图像序列光流计算的基础是基于图像数据的守恒假设，而光照变化、大位移运动等导致的像素点亮度突变现象使得现有的各种图像数据整数阶守恒假设常常出现不连续问题，使得光流计算结果较差.分数阶微分模型是近年来微积分研究领域的热点问题，其具有抗噪性、弱导数性以及记忆性等显著优点.在后续研究中，采用分数阶微分模型代替图像数据守恒假设中传统的整数阶微分模型有望解决由于像素点亮度突变所导致的光流不连续问题.

(2)近年来，基于非局部约束的光流计算模型逐渐成为光流计算的主流方法，但由于目前的非局部约束项只考虑图像邻域像素点的加权约束，常常导致光流估计结果出现“过度分割”现象.因此，在后续研究中应更多考虑基于图像区域的非局部约束策略，利用图像区域平滑抑制“过度分割”现象的产生，同时避免光流计算陷入局部最优.

(3)当图像序列中存在非刚性运动或运动遮挡等现象时，物体或场景表面的像素点或其它特征常常出现“时有时无”的情况，此时基于单目图像序列光流的三维重建技术常常无法获取鲁棒的运动估计与重建结果.在后续研究中应考虑将单目图像序列与双目视觉相结合，利用极线约束对重建模型进一步优化，以提高重建模型的准确性与可靠性.

(4)基于稠密光流的三维重建技术可以重建图像序列中运动物体或场景的稠密结构，充分体现其表面细节信息；而基于特征光流的三维重建技术对图像亮度变化等噪声不敏感，且直线、曲线等特征包含物体或场景更多的拓扑结构.但目前为止，这两类方法基本处于相互平行状态.在后续研究中，应更多考虑将这两类方法进行交叉融合，使得重建结果既能够表现图像细节，又可以获取更多的拓扑信息.

(5)由于基于单目图像序列光流的三维重建结果中通常包含与深度坐标相关的未知参数，使得重建结果的量化评价十分困难.随着消费类深度相机的发展与普及，后续研究中应考虑采用可见光图像与深度图像融合的方法进行三维重建技术研究，利用深度数据对图像中运动物体或场景分层分割，并获取其真实的运动估计与重建结果.

[1]Roberts R,Dellaert F.Direct superpixel labeling for mobile robot navigation using learned general optical flow templates[A].International Conference on Intelligent Robots and Systems[C].Chicago:IEEE,2014.1032-1037.

[2]Nourani-Vatani N,Borges P V K,Roberts J M,et al.On the use of optical flow for scene change detection and description[J].Journal of Intelligent & Robotic Systems,2014,74(3):817-846.

[3]罗寰,王芳,陈中起,等.基于对称差分和光流估计的红外弱小目标检测[J].光学学报,2010,30(6):1715-1720. Luo Huan,Wang fang,Chen Zhong-qi,et al.Infrared target detecting based on symmetrical displaced frame difference and optical flow estimation[J].Acta Optica Sinica,2010,30(6):1715-1720.(in Chinese)

[4]Rhudy M B,Chao H,Gu Y.Wide-field optical flow aided inertial navigation for unmanned aerial vehicles[A].International Conference on Intelligent Robots and Systems[C].Chicago:IEEE,2014.674-679.

[5]Zhou L,Kambhamettu C,Goldgof D B,et al.Tracking nonrigid motion and structure from 2D satellite cloud images without correspondences[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(11):1330-1336.

[6]许鸿奎,江铭炎,杨明强.基于改进光流场模型的脑部多模医学图像配准[J].电子学报,2012,40(3):525-529. Xu Hong-kui,Jiang Ming-yan,Yang Ming-qiang.Registration of multimodal brain medical images based on improved optical flow model[J].Acta Electronica Sinica,2012,40(3):525-529.(in Chinese)

[7]Horn B K,Schunck B G.Determining optical flow[J].Artificial Intelligence,1981,17(1):185-203.

[8]Lucas B D,Kanade T.An iterative image registration technique with an application to stereo vision[A].Proceedings of the 7th International Joint Conference on Artificial Intelligence[C].Vienna:Springer,1981.674-679.

[9]Bruhn A,Weickert J,Schnörr C.Lucas/Kanade meets Horn/Schunck:Combining local and global optic flow methods[J].International Journal of Computer Vision,2005,61(3):211-231.

[10]Brox T,Bruhn A,Papenberg N,et al.High accuracy optical flow estimation based on a theory for warping[A].European Conference on Computer Vision[C].Prague:Springer,2004.25-36.

[11]陈震,张聪炫,晏文敬,等.基于图像局部结构的区域匹配变分光流算法[J].电子学报,2015,43(11):2200-2209. Chen Zhen,Zhang Cong-xuan,Yan Wen-jing,et al.Region matching variational optical flow algorithm based on image local structure[J].Acta Electronica Sinica,2015,43(11):2200-2209.(in Chinese)

[12]Papenberg N,Bruhn A,Brox T,et al.Highly accurate optic flow computation with theoretically justified warping[J].International Journal of Computer Vision,2006,67(2):141-158.

[13]刘骏,祖静,张瑜,等.光照变化条件下的光流估计[J].中国图象图形学报,2014,19(10):1475-1480. Liu Jun,Zu Jing,Zhang Yu,et al.Optical flow estimation method under the condition of illumination change[J].Journal of Image and Graphics,2014,19(10):1475-1480.(in Chinese)

[14]Wedel A,Pock T,Zach C,et al.An improved algorithm for TV-L1 optical flow[A].Proceedings of the Statistical and Geometrical Approaches to Visual Motion Analysis[C].Dagstuhl Castle:Springer,2009.23-45.

[15]Drulea M,Nedevschi S.Total variation regularization of local-global optical flow[A].International Conference on Intelligent Transportation Systems[C].Washington:IEEE,2011.318-323.

[16]项学智,开湘龙,张磊,等.一种变分偏微分多模型光流求解方法[J].仪器仪表学报,2014,35(1):109-116. Xiang Xue-zhi,Kai Xiang-long,Zhang Lei,et al.A method variational partial differential based multi-model optical flow calculation[J].Chinese Journal of Scientific Instrument,2014,35(1):109-116.(in Chinese)

[17]Nagel H H,Enkelmann W.An investigation of smoothness constraints for the estimation of displacement vector fields from image sequences[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1986,8(5):565-593.

[18]Werlberger M,Trobin W,Pock T,et al.Anisotropic Huber-L1 optical flow[A].Proceedings of the British machine vision conference[C].London:BMVA,2009.1-11.

[19]Xu L,Jia J,Matsushita Y.Motion detail preserving optical flow estimation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(9):1744-1757.

[20]Zimmer H,Bruhn A,Weickert J.Optic flow in harmony[J].International Journal of Computer Vision,2011,93(3):368-388.

[21]Brox T,Malik J.Large displacement optical flow:Descriptor matching in variational motion estimation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(3):500-513.

[22]Ayvaci A,Raptis M,Soatto S.Sparse occlusion detection with optical flow[J].International Journal of Computer Vision,2012,97(3):322-338.

[23]Zhang C X,Chen Z,Li M,et al.Anisotropic optical flow algorithm based on self-adaptive cellular neural network[J].Journal of Electronic Imaging,2013,22(1):013038-1-9.

[24]Sun D,Roth S,Black M J.A quantitative analysis of current practices in optical flow estimation and the principles behind them[J].International Journal of Computer Vision,2014,106(2):115-137.

[25]Baker S,Scharstein D,Lewis J P,et al.A database and evaluation methodology for optical flow[J].International Journal of Computer Vision,2011,92(1):1-31.

[26]Roach J W.Determining the movement of objects from a sequence of images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1980,2(6):554-562.

[27]Zhuang X,Huang T S,Abuja N,et al.A simplified linear optic flow-motion algorithm[J].Computer Vision,Graphics,and Image Processing,1988,42(3):334-344.

[28]Chiuso A,Favaro P,Jin H,et al.Structure from motion causally integrated over time[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(4):523-535.

[29]Ozden K E,Schindler K,Van G L.Multibody structure-from-motion in practice[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(6):1134-1141.

[30]王俊,朱利.基于图像匹配-点云融合的建筑物立面三维重建[J].计算机学报,2012,35(10):2072-2079. Wang Jun,Zhu Li.3D building facade reconstruction based on image matching-point cloud fusing[J].Chinese Journal of Computer,2012,35(10):2072-2079.(in Chinese)

[31]Nachimson M,Kovalsky S Z,Shlizerman I,et al.Global motion estimation from point matches[A].International Conference on 3D Imaging,Modeling,Processing,Visualization and Transmission[C].Zurich:IEEE,2012.81-88.

[32]Scaramuzza D.1-point-ransac structure from motion for vehicle-mounted cameras by exploiting non-holonomic constraints[J].International Journal of Computer Vision,2011,95(1):74-85.

[33]Crandall D,Owens A,Snavely N,et al.Discrete-continuous optimization for large-scale structure from motion[A].International Conference on Computer Vision and Pattern Recognition[C].Providence:IEEE,2011.3001-3008.

[34]Sinha S N,Steedly D,Szeliski R.A multi-stage linear approach to structure from motion[A].European Conference on Computer Vision[C].Heraklion:Springer,2010.267-281.

[35]Liu Y,Huang T S.Estimation of rigid body motion using straight line correspondences[J].Computer Vision,Graphics,and Image Processing,1988,43(1):37-52.

[36]Liu Y,Huang T S.A linear algorithm for motion estimation using straight line correspondences[J].Computer Vision,Graphics,and Image Processing,1988,44(1):35-57.

[37]陈震,许强,闫军,等.基于直线光流场的三维检测新方法[J].仪器仪表学报,2012,33(5):1141-1147. Chen Zhen,Xu Qiang,Yan Jun,et a1.New method of 3D detection based on straight-line optical flow[J].Chinese Journal of Scientific Instrument,2012,33(5):1141-1147.(in Chinese)

[38]Taylor C J,Kriegman D J.Structure and motion from line segments in multiple images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1995,17(11):1021-1032.

[39]Mirzaei F M,Roumeliotis S I.Globally optimal pose estimation from line correspondences[A].International Conference on Robotics and Automation[C].Shanghai:IEEE,2011.5581-5588.

[40]Kollmann I R,Reichinger A.3D camera pose estimation using line correspondences and 1D homographies[J].Advances in Visual Computing,2010,64(54):41-52.

[41]Mosaddegh S,Fofi D,Vasseur P.Line based motion estimation and reconstruction of piece-wise planar scenes[A].International Workshop on Applications of Computer Vision[C].Kona:IEEE,2011.658-663.

[42]Liu J,Chen Y,Tang X.Decomposition of complex line drawings with hidden lines for 3D planar-faced manifold object reconstruction[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(1):3-15.

[43]Elqursh A,Elgammal A.Line-based relative pose estimation[A].International Conference on Computer Vision and Pattern Recognition[C].Providence:IEEE,2011.3049-3056.

[44]Bruss R,Horn K P.Passive navigation[J].Computer Vision,Graphics,and Image Processing,1983,21(1):3-20.

[45]Kolev K,Klodt M,Brox T,et al.Continuous global optimization in multiview 3D reconstruction[J].International Journal of Computer Vision,2009,84(1):80-96.

[46]张聪炫,陈震,黎明.基于稠密光流的鲁棒运动估计与表面结构重建[J].仪器仪表学报,2014,35(1):218-225. Zhang Cong-xuan,Chen Zhen,Li Ming.Robust motion estimation and surface structure reconstruction based on dense optical flow[J].Chinese Journal of Scientific Instrument,2014,35(1):218-225.(in Chinese)

[47]Chessa M,Solari F,Sabatini S P.Adjustable linear models for optic flow based obstacle avoidance[J].Computer Vision and Image Understanding,2013,117(6):603-619.

[48]Adiv G.Determining three-dimensional motion and structure from optical flow generated by several moving objects[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1985,7(4):384-401.

[49]Meinhardt L E,Hondt O,Facciolo G,et al.Relative depth from monocular optical flow[A].International Conference on Image Processing[C].Brussels:IEEE,2011.2085-2088.

[50]Calway A.Recursive estimation of 3D motion and surface structure from local affine flow parameters[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(4):562-574.

[51]Lee D J,Merrell P,Wei Z,et al.Two-frame structure from motion using optical flow probability distributions for unmanned air vehicle obstacle avoidance[J].Machine Vision and Applications,2010,21(3):229-240.

[52]Horn B K P,Weldon J E J.Direct methods for recovering motion[J].International Journal of Computer Vision,1988,2(1):51-76.

[53]Mitiche A,Hadjres S.MDL estimation of a dense map of relative depth and 3D motion from a temporal sequence of images[J].Pattern Analysis & Applications,2003,6(1):78-87.

[54]Sekkati H,Mitiche A.A variational method for the recovery of dense 3D structure from motion[J].Robotics and Autonomous Systems,2007,55(7):597-607.

[55]Perriollat M,Hartley R,Bartoli A.Monocular template-based reconstruction of inextensible surfaces[J].International Journal of Computer Vision,2011,95(2):124-137.

[56]Mitiche A,Sekkati H.Optical flow 3d segmentation and interpretation:A variational method with active curve evolution and level sets[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(11):1818-1829.

[57]Zhang C X,Chen Z,Li M,et al.Direct method for motion estimation and structure reconstruction based on optical flow[J].Optical Engineering,2012,51(6):067004-1-14.

[58]Ummenhofer B,Brox T.Dense 3D reconstruction with a hand-held camera[A].Proceedings of the 34th Symposium of the German Association for Pattern Recognition[C].Graz:Springer,2012.103-112.

[59]张聪炫,陈震,黎明.金字塔光流三维运动估计与深度重建直接方法[J].仪器仪表学报,2015,36(5):1093-1105. Zhang Cong-xuan,Chen Zhen,Li Ming.Direct method for motion estimation and depth reconstruction based on pyramid optical flow[J].Chinese Journal of Scientific Instrument,2015,36(5):1093-1105.(in Chinese)

[60]Cubber G,Sahli H.Partial differential equation-based dense 3D structure and motion estimation from monocular image sequences[J].IET Computer Vision,2012,6(3):174-185.

张聪炫 男，1984年7月出生于河南省焦作市.分别于2007年和2014年在南昌航空大学和南京航空航天大学获得学士和博士学位.现为南昌航空大学讲师，硕士生导师.主要研究方向为图像检测与智能识别.

E-mail:zcxdsg@163.com

陈 震(通信作者) 男，1969年11月出生于江西省九江市.分别于1993、2000和2003年在西北工业大学获得学士、硕士和博士学位.现为南昌航空大学教授，博士生导师.主要研究方向为计算机视觉、图像处理与模式识别.

E-mail:dr-chenzhen@163.com

黎 明 男，1965年2月出生于江西省樟树市.分别于1985年、1990年和1997年在上海交通大学和南京航空航天大学获得学士、硕士和博士学位.现为南昌航空大学教授，博士生导师.主要研究方向为图像处理与模式识别、智能计算.

E-mail:limingniat@hotmail.com

Review of the 3D Reconstruction Technology Based on Optical Flow of Monocular Image Sequence

ZHANG Cong-xuan1,2,CHEN Zhen1,2,LI Ming1,2

(1.KeyLaboratoryofNondestructiveTesting,MinistryofEducation,NanchangHangkongUniversity,Nanchang,Jiangxi330063,China; 2.SchoolofMeasuringandOpticalEngineering,NanchangHangkongUniversity,Nanchang,Jiangxi330063,China)

The research on 3D motion estimation and structure reconstruction of the object or scene based on the monocular image sequence optical flow is important in computer vision,image processing and pattern recognition,and the research achievements are applied in many fields.such as robot vision,unmanned aerial vehicle(UAV) navigation,driver assistance system,medical image analysis,and so on.Firstly,the research progress of the technologies of the monocular image sequence optical flow estimation and 3D reconstruction is reviewed and analyzed from the aspects of accuracy and robustness.Secondly,the test image sequences of Middlebury database are employed to make comparison among the optical flow methods of HS,LDOF,CLG-TV,SOF,AOFSCNN and Classic+NL,and the direct and indirect reconstruction methods of Adiv,RMROF,Sekkati and DMDPOF based on optical flow are compared.Through the comparison results,the advantages and disadvantages of the methods are pointed out,and the characteristics and applications of the methods are generalized.Finally,the limitations and robustness of the models of optical flow estimation and 3D reconstruction in brightness changing,non-rigid motion,motion occlusion and blur are summarized,and the solutions by the fractional order differential model,non-local constraint,stereo vision and depth cue are presented.

monocular image sequence;optical flow;motion estimation;3D reconstruction;hard scene;robustness

2015-11-24;

2016-01-19;责任编辑:覃怀银

国家自然科学基金(No.61401190,No.U1233125,No.61462062);江西省主要学科学术带头人培养计划项目(No.201208421);江西省自然科学基金重点项目(No.20133ACB20004);江西省科技落地计划项目(No.201408083);航空科学基金(No.2015ZC56009);江西省优势学科团队计划项目(No.20152BCB24004);无损检测技术教育部重点实验室开放基金(No.ZD201529001)

TP391

A

0372-2112 (2016)12-3044-09

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.12.033