基于地形高度域的数据压缩算法研究
2017-01-10代双凤潘卫国
翟 锐,吕 科,代双凤,潘卫国
(中国科学院大学工程管理与信息技术学院,北京,100049)
基于地形高度域的数据压缩算法研究
翟 锐,吕 科,代双凤,潘卫国
(中国科学院大学工程管理与信息技术学院,北京,100049)
随着遥感技术的发展,地形数据规模越来越大,远远超过了内存处理的范围,成为急需解决的问题.通过数据压缩提高系统吞吐量是常用技术之一,随着GPU技术的快速发展,传统的压缩算法无法充分利用GPU的能力.鉴于此,本文提出了一种基于GPU的地形数据压缩方法,实现了高度域和位置信息的压缩.不同于其他的算法仅对高度或位置进行压缩,本文的主要贡献在于将地形的位置和高度同时进行处理,当前顶点的所有信息都可以根据当前分段计算得到.算法对地形的高度域进行贝塞尔曲线的近似,保存每个顶点的差值,实现有损和无损的相结合的高比率的压缩.通过与传统方法的比较,实验结果表明,能够取得很好的压缩效果.
数据压缩;地形渲染;图形处理器
1 引言
大规模地形渲染是计算机图形学的主要研究内容之一,广泛应用于虚拟现实、地理信息系统、飞行模拟和游戏等领域.随着遥感技术的发展,数字地形数据的分辨率日益增高,数据规模越来越大.近几年,GPU计算能力得到了飞速提升,处理速度比从内存传输至图形显卡的速度更快,目前的渲染算法中已从早期处理单个三角形变为处理三角形块,因此数据传输成为地形渲染的瓶颈之一,而通过对地形数据采用压缩技术增大系统的吞吐量可以有效的解决这一问题,所以压缩技术的研究已成为国内外研究的热点.
在地形渲染中,数据压缩可用于多种数据:包括纹理、高度域或位置等.根据压缩方法的不同,可以分为有损压缩、无损压缩和两种相结合的方法.针对于不同的应用场景,需求也有一定的差异.例如,对于无交互的应用,解码速度要求相对较低,可以使用无损的压缩方法.而对渲染速度要求较高的场合,可能需要采用有损的压缩方法.结合目前的GPU技术,本文提出了一种无损和有损相结合的地形位置信息和高度域信息的压缩算法,可以实现高比率的数据压缩,提高系统的吞吐量.
2 国内外研究现状
根据数据结构的不同,地形渲染算法可以分为两大类:基于规则网格的算法如实时优化自适应网格算法翟 锐:基于地形高度域的数据压缩算法研究(Real-Time Optimally Adapting Mesh,ROAM)[1]和基于不规则三角网的算法(Triangulated Irregular Network,TIN),如渐进网格(Progressive Mesh)[2]等.与不规则网格相比,规则结构更适合基于GPU的并行的环境,统一的结构更易于编码与实现,在压缩领域也是如此.本文的研究内容是基于约束四叉树的位置信息和高度域信息的压缩.
根据压缩策略的不同,可以分为有损压缩、无损压缩或两者相结合的方法.有损压缩常被用于实时渲染领域,对渲染速度要求较高的系统.例如Gerstner[3]处理原始地形数据的子集来压缩高度域,通过线性的插值计算被删除的顶点.Kim[4]等将地形数据进行小波变换来构建近似的三角化网格.但是这些方法编码速度较慢.除了实时渲染系统,有损压缩还用于分布的网络传输中[5].
无损压缩方法中,根据相邻顶点的信息预测顶点的高度,使用通用的无损压缩方法对预测误差进行编码.早期的一些算法中,使用各种方法对编码进行预测,如霍夫曼编码、拉格朗日乘数优化的线性方法或算术编码[6,7]等.这些方法的压缩效率比直接使用数字图像编码的压缩效率要高,但处理数据的方式是顺序的,不适用于并行的压缩.还有一些算法将高度域映射到更高阶的表面[8],实现基于点的并行,不过这些方法提出的时间较早,在可编程的GPU之前出现,并没有考虑到目前的并行的框架.也有一些算法将图像的压缩算法应用于地形的压缩方法中.与图像的灰度压缩不同,在一些地形的压缩算法中,地形的压缩算法需要考虑到地形的结构,而在灰度图的压缩中通常没有考虑到这一点.
最近的一些压缩方法在GPU上处理数据.Dick等[9]使用与文献[3]中类似的编码,在GPU上进行了实现,不过该方法只对位置进行了压缩,并没有针对处理高度域进行处理.Lindstrom[10]等使用线性预测方法,不过这种方法中每一块的解压实际上是顺序的过程,因为待解压的顶点的高度是根据之前压缩的顶点获得,无法获取任意顶点的值.此外,Stookey[11]采用了有损压缩的方法并在网络上实现了分布传输.Olanda[12]使用小波分块的金字塔用于在线的三维可视化系统.Li[13]等人采用类似于文献[11]中的方法进行5D的数据压缩,并使用CUDA解方程.但是上述方法需要迭代过程,本质上仍然是顺序的方法.Dore[14,15]等人最近提出了一种基于高度域压缩的算法,将一块地形的高度值近似到贝塞尔曲面,只需保存控制点的信息,运行时动态的计算顶点的高度.但这种方法中的分块只能是一个层次,而且只对顶点进行了压缩,并没有结合位置信息.Niski[16]将高度域作为纹理进程处理,利用图像压缩的算法对高度域进行压缩.但该方法没有考虑到位置的压缩,因此不够灵活.随着通用图形处理器(General Purpose GPU,GPGPU)的发展,研究者使用并行技术实现经典的编码,如基于CUDA实现的霍夫曼编码[17],JPEG2000编码[18]等.不过这些编码灵活性有限,而且将其用于地形压缩时的效果还需要进一步的考虑.
根据上述的研究基础,本文提出了一种对位置信息和高度信息同时进行压缩的压缩方法.与之前的算法不同,应用本文的算法,在获取任意点的位置和高度时,只需要局部的参考信息,并且结合GPU并行环境,实现了完全的并行数据处理.实验结果表明,本文所提算法在数据压缩比和运行效率上都得到了很大的提高.
3 算法
在地形渲染领域,约束四叉树是一种常见的数据结构,与不规则的三角形网格相比,更加适用于基于GPU的环境.本文所提方法采用约束四叉树的数据结构,并对地形数据的位置信息采用无损压缩方法,对地形数据的高度信息可以采用有损或无损的压缩方法.
地形数据的预处理流程如图1所示,包含如下几个步骤:首先是将显示所需的地形数据以约束四叉树的结构表示并三角化.然后对地形的位置信息和高度信息分别进行压缩.
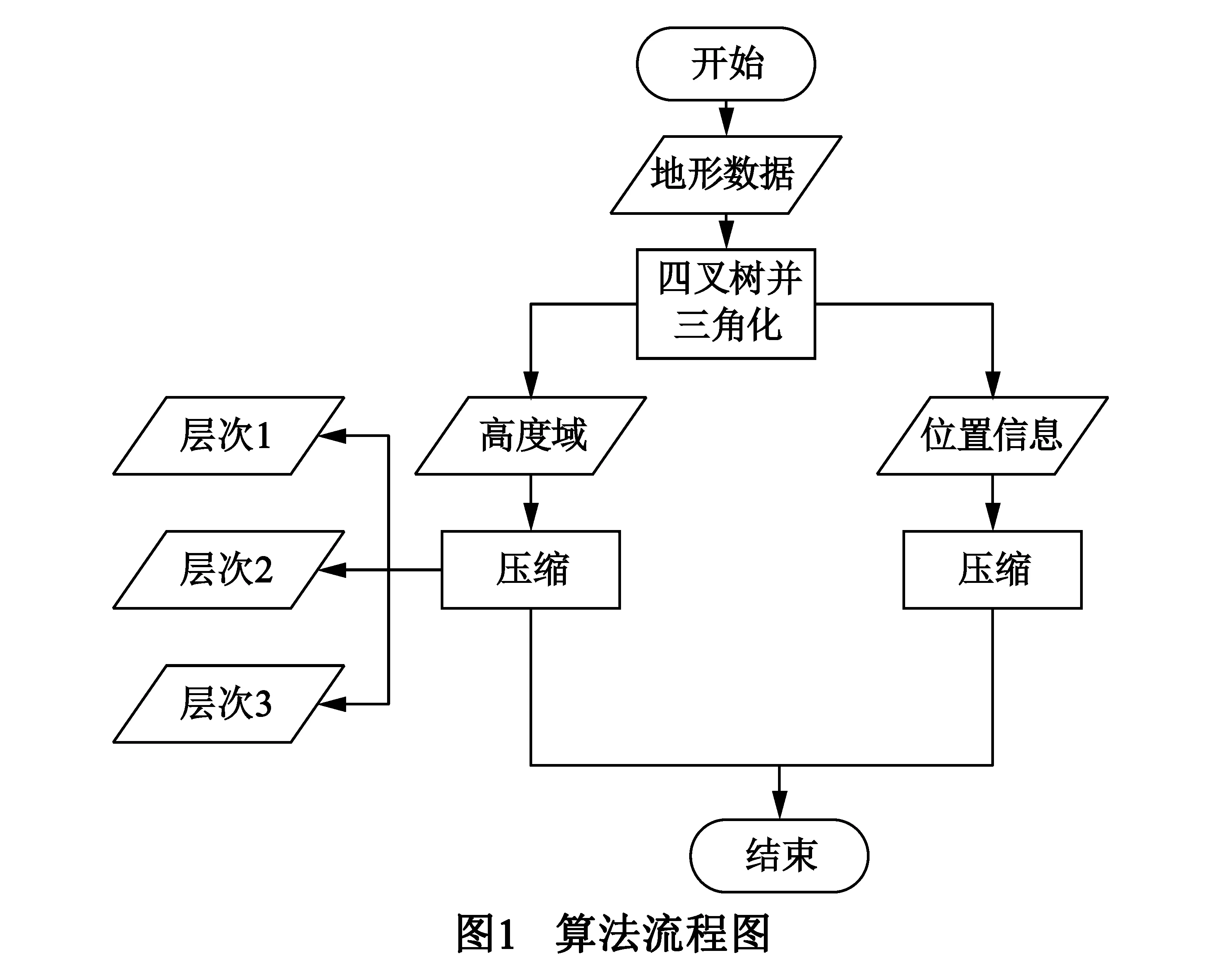
3.1 位置信息压缩
对于位置信息的压缩时,借鉴了Gerstiner提出约束四叉树的序列化方法[3].主要思想如下:对于每个网格,初始化阶段时,选择两个顶点并记录其位置信息,然后根据前两个顶点和标识符计算第三个顶点的信息,重复该步骤直至访问所有的顶点.
构建链表的步骤如下:首先根据观察者与该块的距离等信息决定该块的细分层次,随后进行三角化.三角化后,选择其中一个三角形的两个顶点作为初始顶点,根据该三角形的最后一个顶点的位置和与前两个顶点的相对位置决定三角形的类型.完成当前三角形的构建后,根据该顶点和其中一个起始顶点(由方向决定)作为下一个三角形的初始顶点,重复上述构建过程直至访问所有的顶点.
三角形包括三种类型:直角边到直角边,直角边到斜边,斜边到直角边.方向为两种:顺时针和逆时针.图2表示了这几种情况,压缩时,已知顶点为V0和V1,根据V2的位置决定三角形的类型.解压时,对于直角三角形的三个顶点V0、V1、V2,已知顶点V0和V1,可以根据两个顶点的位置和三角形的类型计算得到另一个顶点V2的位置信息.
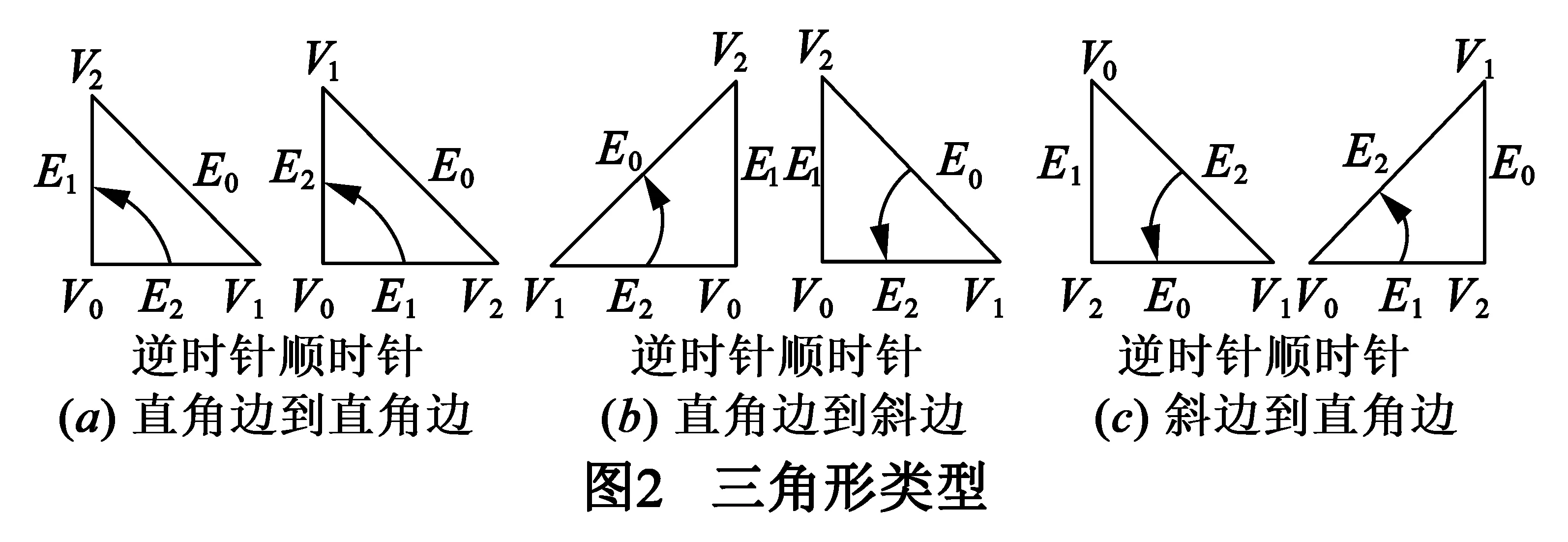
除了顶点的位置信息进行编码外,还需要处理顶点的高度信息.本文采用了一种分层的方法对高度域进行压缩,将高度域分为多个层次,然后分别对每一层进行处理.第一层是对整个高度域的粗糙近似,第二层在第一层的基础上增加了细节,最后一层是与真实地形的最终的差值,其中第二层和第三层的值可能都为0,因此在实际中可能不需要保存这些数据.
一块数据可能包含多个子带,每个子带包含头信息和数据信息.一块数据可能包含多个头信息和多个顶点,之所以这样设计是可以灵活的添加和删除顶点,除非结构有大的变化,无需对结构进行大的调整.
表1为本文所采用的数据结构,可以分为头信息和每个顶点的信息.头信息包含当前子带中的顶点的共有信息,包括顶点个数、子带中第一个顶点的高度和最后一个顶点的高度.顶点数表明每一个贝塞尔曲线覆盖多少个顶点.对于地形变化较大的区域,如果包含的顶点数过多,可能导致差值1和差值2较大,反而不能得到好的压缩效率.相比于粗糙的区域,平坦区域中的贝塞尔曲线可能可以包含更多的顶点也能有较好压缩比率.除了第一个和最后一个顶点,其他的顶点使用两个字段保存差值信息,实际应用中,根据实际需求,可以决定是否对两个差值进行无损压缩.运行时,根据头信息中的贝塞尔参数和每个顶点自带的信息计算相应顶点的高度.

表1 数据结构
3.2 高度域压缩
上一节中对数据的编码和结构进行了介绍,本节中主要介绍如何使用贝塞尔曲线对高度域进行模拟.由于地形高度域具有规则性,可以使用一些专门的曲线对其进行近似.贝塞尔曲线是一种常用的构建地形的工具,只需要几个控制点信息即可计算曲线上顶点的位置.
在大多数的场合中,原始的高度域和根据贝塞尔曲线构建的层次1的差值的范围集中在0的周围.这样的分布在基于预测的方法中是非常常见的.大多数的差值可以使用一个相对较小的位数保存.若还不满足需求,将最终的值保存在层次3中.此外,层次2和层次3还可以进一步的压缩.
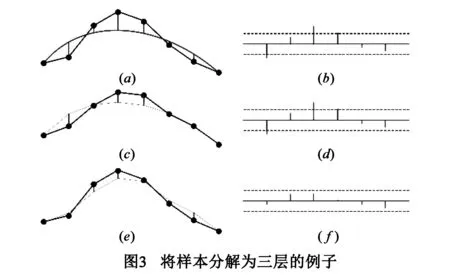
实际中,可以使用二阶或更高阶的贝塞尔进行模拟,阶数越高,模拟结果越精确.但是如果阶数越高,导致计算开销过大,因此,在实际应用中,通常使用二阶的贝塞尔曲线进行模拟,通过修改每个贝塞尔曲线覆盖的顶点个数修正压缩率.二阶贝塞尔曲线包含两个顶点V0,Vn和一个控制点C0.其中V0和Vn高度为H0和Hn,C0是贝塞尔参数的控制点的值.
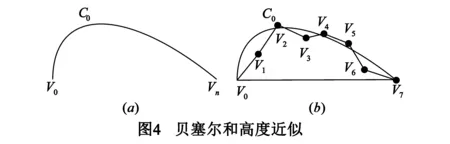
已知顶点V0,Vn的信息,只需计算控制点C0的位置,可以考虑使用最小二乘法对贝塞尔曲线进行拟合.
解压时,中间顶点的高度通过下述的公式计算得到.每个顶点保存了一个参数t,相应顶点的高度H(t)的计算方法如式(1)所示:
H(t)=(1-t)2H0+2t(1-t)H1+t2H2,t∈[0,1]
(1)
应当指出的是,每个顶点的高度可以并行获得.已知V1和Vn的高度,其他顶点的高度V2,V3,…,Vn-1可以独立计算.差值1可以以稀疏矩阵方式存储在层次2.差值2存储在第3层.如果为了直接和快速的访问每个最终的残留,可以不对差值进行压缩.
3.3 基于GPU的实现
目前GPU不仅用于绘制,由于其具有很强的浮点数计算能力,被广泛应用在通用计算领域[19~21].
在基于CUDA的压缩中,压缩在不同的核中执行,其中一个核计算近似的贝塞尔曲线,另外两个核计算层次2和层次3,将中间结果保存在访问速度较快的共享存储器中.计算近似的贝塞尔曲线时,分别对每个高度域顶点分配一个线程,使用最小二乘法实现对曲线的近似,对于大小为32×32的线程块,可以计算128个分段的信息.构建层次2时,将高度值和上一个步骤的近似做差值计算,然后将最终的残留保存在层次3中.
目前的图形硬件支持可编程的着色器,在渲染每一帧时,将可见的未缓存的块进行压缩,并传输到显存中,在GPU中解压.在对某一块数据进行解码时,首先读取带头信息,加载到顶点缓冲区中.根据带头信息得到第一个顶点和最后一个顶点的高度值,结合子带中两个顶点V0、V1和下一个顶点的类型得到第三个顶点的位置.然后按照上文中的步骤构建其他的三角形.通过贝塞尔曲线得到近似高度,根据实际需要与两个差值相加,得到最终的顶点高度.
压缩和解压步骤分别可以并行的执行,压缩过程中同时对多个带进行计算.在解压过程中,可以分别计算每个段中的顶点的详细位置,而无需考虑其他的信息.整个系统可以并行的执行,压缩和解压过程中的最小单位即贝塞尔曲线包含的顶点个数,例如一个贝塞尔曲线包含10个顶点,实现了细粒度的并行.
4 实验与结果分析
本节中,我们通过实验对本文算法进行验证和分析.数据对象是结构较为复杂的Pudget Sound和结构较为平坦的夏威夷的数据,如图5所示.实验运行环境为:微软Win7 32位系统,Intel i7-3610,2.3GHz内存,3.14GB内存,显卡为NVIDIA GeForce GT630M.
在未经压缩的结构中,每个顶点占用32bit,其中高度域12bit,位置x和y分别是10bit,共32bit.每个三角形占用96bit.经过本文方法的压缩后,头文件中,顶点数为6bit,高度1和高度2共为24bit,两个贝塞尔参数共为16bit.共计42bit.对于单个顶点而言,第一个顶点只需要保存位置信息20bit,第二个顶点20bit和差值2~7bit,共计22~27.顶点3至(n-1)为类型3bit和插值2~7bit,共计5~10bit.最后一个顶点3bit.这些顶点所占用的bit数共计:[5(n+6),10(n+2)]bit,共计可组成n-2个三角形.如果n=8,8个顶点能够组成6个三角形,占用的空间共计为70~100bit,与之前每个三角形占用96bit相比,压缩效率为:5.76~8.2.在实际应用中,由于差值可能为0,压缩效率可能更高.
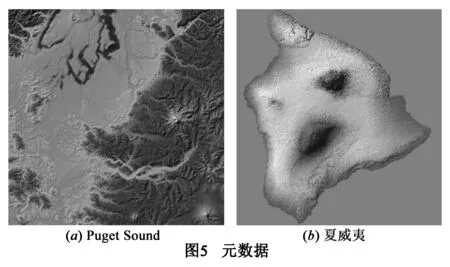
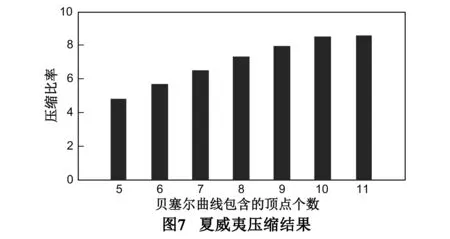
表2和表3分别表示了Puget Sound和夏威夷的数据使用不同的贝塞尔个数的压缩效率,第一行表示贝塞尔参数包含的顶点个数,第二行表示其压缩效率.图6和图7是与表2和表3相对应的柱状图的显示.横轴表示贝塞尔曲线包含不同的顶点时的压缩效率,纵轴表示相应的压缩率.

表2 Puget Sound压缩结果

表3 夏威夷压缩结果
图6和图7中的数据表明,对于单个地形而言,贝塞尔曲线包含的顶点增多,压缩率会逐步提高,但是到达某临界值之后,压缩效率会有所下降,需要额外空间保存差值2和差值3的值.对于不同的地形而言,压缩效率也有所不同,在地形较为平坦的区域,压缩的效率更高.而且出现拐点的贝塞尔曲线包含的顶点的值也不同,平坦区域的拐点的值大于粗糙的区域的拐点的值.总体上而言,平坦的数据的压缩效果要好于结构复杂的数据的压缩效果.
使用经典的算法ZIP对数据进行压缩,其压缩比率大概为2.5∶1,而本文所提算法相对于结构复杂的数据的平均压缩比率为6.3∶1,相对于平坦的数据的平均压缩比率为7.06∶1.可以看出,本文所提算法具有更好的压缩效果.由于压缩过程中包含复杂的计算,因此解压速度要快于压缩速度.不过贝塞尔曲线包含的顶点个数对压缩和解压的速度不会有太大的影响,这是因为实际的操作基本是基于每个顶点执行.实际应用中,每秒可以解压108的顶点,满足了实时的需求.如果提高压缩的速度,可以更进一步的提高吞吐量.

5 结语
本文提出了一种新的高度域快速压缩和解压方法,可以充分利用GPU的并行功能.实现了有损和无损的压缩.我们的方法在两个无关的数据中进行了试验,实验结果表明,能够实现非常高效的压缩效果.与传统的压缩方法相比,我们的压缩率要远远高于其压缩效率,随着数据规模的增大,可能实现进一步的提升.
本文的方法可以用于大规模的地形数据处理的二次处理中.解压速度和经典的基于GPU的解压速度相当.此外,系统还可以与其他压缩方法相结合.下一步的工作中,我们将考虑更高阶的贝塞尔曲线能否取得更好的压缩效率,以及如何快速的计算高阶贝塞尔曲线的控制点.
[1]Duchaineau M,Wolinsky M,Sigeti D E,et al.ROAMing terrain:real-time optimally adapting meshes[A].Visualization'97[C].Phoenix,AZ,USA:IEEE,1997.81-88.
[2]Hoppe H.View-dependent refinement of progressive meshes[A].ProcSiggraph[C].Los Angeles,USA:ACM,1997.189-198.
[3]Gerstner T.Multi-resolution visualization and compression of global topographic data[J].Geoinformatica,2003,7(1):7-32.
[4]Kim J K,Ra J B.A real-time terrain visualization algorithm using wavelet-based compression[J].Visual Computer,2004,20(2):67-85.
[5]Xie Z,Marcus A,Randolph F,Barbara C,et al.Progressive transmission of lossily compressed terrain[A].Conferencialatinoamericana de informática (CLEI 2008)[C].Santa Fe,Argentina:2008.8-12.
[6]Kidner B,Derek S.Advances in the data compression of digital elevation models[J].Computers & Geosciences,2003,29(8):985-1002.
[7]Inanc M.Compressing terrain elevation datasets[D].NY,USA:Rensselaer Polytechnic Institute Troy,2008.
[8]Kidner B,Derek S.Storageefficient techniques for representing digital terrain models[A].Innovations in GIS 4[C].London,England:Taylor & Francis,1997.25-41.
[9]Dick C,Schneider J,Westermann R.Efficient geometry compression for GPU-based decoding in realtime terrain rendering[J].Computer Graphics Forum,2009,28(1):67-83.
[10]Lindstrom P,Cohen D.On-the-fly decompression and rendering of multiresolution terrain[A].Proceedings of the 2010 ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games[C].Bethesda,MD,USA:ACM,2010.65-73.
[11]Jared S,Randolph F,Xie Z,et al.Parallel ODETLAP for terrain compression and reconstruction[A].Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems[C].Irvine,California,USA:ACM,2008.17.
[12]Olanda R,Pérez M,et al.Terrain data compression using wavelet-tiled pyramids for online 3D terrain visualization[J].International Journal of Geographical Information Science,2013,28(2):407-425.
[13]Li Y.CUDA-accelerated HD-ODETLAP:A high dimensional geospatial data compression framework[D].NY,USA:Rensselaer Polytechnic Institute Troy,2011.
[16]Niski K,Purnomo B,Cohen J.Multi-grained level of detail using a hierarchical seamless texture atlas[A].Proceedings of the 2007 Symposium on Interactive 3D Graphics and Games[C].Seattle,WA,USA:ACM,2007.153-160.
[17]Rahmani H,CihanT,Cuneyt A.A parallel huffman coder on the CUDA architecture[A].Visual Communications and Image Processing Conference,2014 IEEE[C].Valletta,Malta:IEEE,2014.311-314.
[18]Lee J,Kim B,Yoon K.CUDA-based JPEG2000 encoding scheme[A].International Conference on Advanced Communication Technology[C].Pyeongchang,Korea:IEEE,2014.671-674.
[19]赵星,胡晶晶,潘晓川,张朋.一种新的基于GPU实现的锥束CT正投影算法[J].电子学报,2009,37(6):1165-1169. Zhao Xing,Hu Jingjing,Pan Xiaochuan,Zhang Peng.A novel GPU based cone beam CT forward projection method[J].Acta Electronica Sinica,2009,37(6):1165-1169.(in Chinese)
[20]杨正龙,金林,李蔚清.基于GPU的图形电磁计算加速算法[J].电子学报,2007,35(6):1056-1060. Yang Zhenglong,Jin Lin,Li Weiqing.Accelerated GRECO based on GPU[J].Acta Electronica Sinica,2007,35(6):1056-1060.(in Chinese)
[21]王纲,季振洲,张泽旭.大规模真实感雪景实时渲染[J].电子学报,2012,40(9):1746-1751. Wang Gang,Ji Zhenzhou,Zhang Zexu.Large scale realistic snow scene real-time rendering[J].Acta Electronica Sinica,2012,40(9):1746-1751.(in Chinese)

翟 锐 男,1981年生于河南焦作,中国科学院大学在读博士生,主要研究方向为数字图像处理、计算机图形学、三维可视化.
E-mail:zhairui11b@mails.ucas.ac.cn

吕 科 男,1971出生于宁夏西吉,教授,博士生导师,主要研究方向为数字图像处理、计算机图形学、智能信息处理技术.
E-mail:luk@ucas.ac.cn
Research on Terrain Height Field Compression Algorithm
ZHAI Rui,LÜ Ke,DAI Shuang-feng,PAN Wei-guo
(CollegeofEngineeringandInformationTechnology,UniversityofChineseAcademyofSciences,Beijing100049,China)
With the development of remote sensing technology,the size of terrain is growing rapidly,and far beyond the scope of main memory,has become an urgent problem.Data compression is a popular technology to increase system throughput.With the rapid development of GPU(Graphics Processing Unit) technology,the traditional compression algorithms cannot take full advantage of the ability of the current GPU.In this paper,we propose a GPU-based terrain data compression method,and achieve a high rate compression of terrain height field and location.Comparing to other algorithms,the main contribution of our algorithm is that the compression of terrain height filed and position is executed in the same time,and all the information of a node can be calculated according to the presentstrip.For terrain height domain,we firstly make Bezier curve approximation,then save the difference.After the steps above,we can achieve high compression ratio.By comparison with traditional methods,we get reasonable experimental results.
data compression;terrain rendering;graphics processing unit (GPU)
2015-04-09;
2015-05-05;责任编辑:梅志强
国家自然科学基金(No.61271435);北京市自然科学基金重点项目(No.4141003)
TP302.7
A
0372-2112 (2016)12-2894-06
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.12.012
