力负载对超声切割声学系统谐振频率及谐振阻抗的影响

纪华伟， 虞文泽， 胡小平

(杭州电子科技大学 机械工程学院，杭州 310018)

力负载对超声切割声学系统谐振频率及谐振阻抗的影响

纪华伟， 虞文泽， 胡小平

(杭州电子科技大学 机械工程学院，杭州 310018)

针对在蜂窝复合材料超声波切割加工中，超声切割系统在受力之后会出现系统失谐，振幅不足甚至停振的现象，对声学系统受力之后的阻抗值以及谐振频率进行研究。利用四端网络法，通过分析变幅杆、压电陶瓷以及端盖等组成声学系统各部分输入输出特性，提出了声学系统的整体设计方程，得出了声学系统的阻抗值和频率方程以及负载﹑电流与振幅的关系式，并对超声切割系统的受力模型进行分析;通过对超声切割声学系统施加单向力，分析受力之后的声学系统阻抗值和谐振频率，得出声学系统受力对系统阻抗值和谐振频率的影响规律。实验结果表明：增加三个方向力之后，系统的阻抗值和谐振频率都会上升;随着力负载的增加，Y、Z方向施加力负载时的系统阻抗值比X方向施加力负载时增加得更快，而在系统谐振频率方面，X、Z方向施加力负载时谐振频率的增量比Y方向施加力负载时更大，在实际应用中应减小敏感方向的力;研究成果可为实际加工蜂窝复合材料提供理论指导。

超声切割系统；力负载；受力模型；阻抗值；谐振频率

蜂窝复合材料以其具有的高比强度和比刚度等优点，在航空航天领域得到了越来越广泛的应用。对蜂窝复合材料进行高速铣削能得到不错的加工质量，但是这种加工方法采用的是粉碎切屑的方法，会产生大量的粉尘，对人体有巨大的危害，采用超声加工的方法可以避免这样的危害[1]。超声切割是针对蜂窝复合材料粗加工提出的，利用高频振动对其进行切割，事实证明这种方法在保证加工质量的同时又有十分高的加工效率。

对于超声加工来讲，声学系统的设计至关重要。超声切割声学系统的设计方法有传统解析法﹑阻抗分析法﹑四端网络法[2-3]等。北方工业大学的曾凡冲[4]针对对称和非对称的压电换能器提出包含连续模型﹑集中参数模型等多种理论模型；赵福令等[5]完善了变幅杆的四端网络法的理论设计，为后期的整体设计提供了良好的基础；HARADA等[6]研究了超声车削中超声车削力与切削速度﹑切削深度以及切削质量之间的关系，在实验中检测出超声切削力的实际形状；ZHANG等[7]为了控制超声切削的深度以及减少超声切削力，对输入电压﹑切削深度以及超声切削力三者之间的关系进行了研究；美国和俄罗斯的EFIM SH.STATNIKOV等[8]对超声冲击力与冲击深度的关系进行了研究；ZHU等[9]提出了超声珩磨的受力模型；张云电等[10]对超声珩磨受力与系统谐振频率之间的关系进行了实验。

大部分针对超声切割声学系统的设计方法涉及到十分复杂的参数表达式[11]，研究方法通常都是将声学系统的各个部分分开来设计，缺乏整个声学系统的统一表达式，使得针对整个声学系统的理论分析变得很困难[12-15]。目前，对于蜂窝复合材料超声切割声学系统的研究略显不足，超声切割力模型及其受到不同方向的力之后的声学系统的阻抗值及谐振频率的变化规律尚不明确，超声切割声学系统在实际加工中不够稳定。

基于以上问题，针对蜂窝复合材料切割加工过程中超声切割系统在受力之后出现系统失谐，振幅不足甚至停振等现象，通过四端网络法将组成声学系统的变幅杆、压电陶瓷以及端盖结合在一起进行研究，得出整个声学系统输入阻抗表达式及频率方程。在此基础上对声学系统的受力模型进行分析，对超声切割声学系统施加X、Y、Z三个方向的力并通过阻抗分析仪对受力之后的声学系统阻抗值和谐振频率进行测量，得出声学系统受力对系统阻抗值和谐振频率的影响规律。

1 基于四端网络法的超声切割系统整体阻抗模型

1.1 变幅杆输入输出特性分析

对于任意函数的纵振杆都可以等效成一四端网络(如图1)。

图1 变幅杆四端网络示意图

一维纵振杆波动方程为：

(1)

结合边界条件F1=-F(0);F2=-F(L);V1=V(0);V2=-V(L)。

可得到变幅杆的输入输出关系式

(2)

故变幅杆的四端网络表达式为：

(3)

以圆锥形变幅杆为例，则变幅杆四端网络中的参数为：

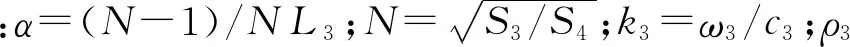
1.2 压电陶瓷输入输出特性分析

压电陶瓷不同于变幅杆，其并不是一个纯粹的力输入、力输出的元件，而是将电能转化成机械能的元件，压电陶瓷的两个输出端分别连接着压电换能器的前端盖和后端盖，而变幅杆及负载都是连接在前端盖上，所以只需要研究前端盖方向上的等效模型即可。

压电陶瓷的输入与输出关系同样可以用四端网络来表示(见图2)。

图2 压电陶瓷四端网络示意图

选择圆柱形压电陶瓷，取长度为Lp，面积为Ap的压电陶瓷，在距离压电陶瓷端面为Z处取微分单元dZ为分析对象。

图3 压电陶瓷模型

当压电陶瓷满足一维纵振时

T1=T2=0

E1=E2=0

D1=D2=0

对于无损耗的压电材料，e型压电方程为：

(4)

结合牛顿第二定律可得和电荷守恒方程可得：

(5)

式中:ρ为密度。

又因

(6)

将式(4)和式(6)代入式(5)可得:

(7)

利用分离变量的方法，可将位移和电势的空间和时间函数表示为：

(8)

将式(8)代入式(7)可得：

(9)

根据式(9)可得到解:

(10)

利用边界条件即可求得C1，C2，C3，C4。

同理可解得：

(11)

通过电位移在电极面积上的积分，再对时间求导就可得到电流，通过位移对时间的微分可得到压电陶瓷的振速，则

(12)

根据式(12)以及边界条件:

u3(z=0)=0,φ(z=0)=0

T3(Z=Lp)=F3/Ap,φ(Z=Lp)=-U

可得到压电陶瓷四端网络传递参数：

1.3 超声切割系统整体阻抗模型

将压电陶瓷与其余部分结合一起，则超声切割声学系统可以等效成如图4所示的四端网络。

图4 声学系统四端网络

前端盖采用圆柱形，因此可将前端盖看成一节圆柱型变幅杆，其四端网络参数的推导方法与变幅杆相同。通过计算，可得前端盖四端网络参数为：

式中:ρ2为前端盖密度;S2为前端盖端面面积;c2为前端盖中的声速;L2为前端盖长度;k2=ω2/c2。

由图4可得到传输矩阵：

(13)

(15)

此处的负载为刀具与力的综合负载，由于刀具负载不存在变化，为固定值，故只考虑力的变化规律。

当ZF=0，即不存在负载时

(16)

当Zi为纯阻时，可得频率方程

(17)

在变幅杆中放大系数M表示输出振速与输入振幅的比值，根据力-电类比理论，振速类比于电流，力类比于电压，本文中输入电流与输出振速的比值M可认为是声学系统整体的放大系数，则：

(18)

可知刀尖处的瞬时位移为S=Asin(2πft+b)，则刀尖瞬时速度为Vo=2πfAcos(2πft+b)，故刀尖的速度与振幅的关系为V=2πfA。将上述条件带入公式(18)可得到振幅﹑负载和电流的关系式

打定了主意，孟导抽空就到古玩市场里溜达，结交了不少商贩。其中，跟古玩市场里的名人叶总走得最近。孟导只要是工作不忙，就会到叶总店里闲逛。其间孟导也买过几个花瓶器皿，不过既然是跟行家里手做交易，套白狼什么的也就没指望了。孟导渴望扬名立万的心情得不到满足，内心越发迫切，天天和叶总讨论哪里有埋没于民间的奇珍异宝。

(19)

2 负载阻抗超声切割力模型分析

将式(19)中的负载阻抗ZF具体到实际的超声切割力进行分析。

如图5所示，超声切割声学系统在切割材料时存在两种运动，分别为沿声学主轴方向的超声振动以及沿水平方向的进给运动，由于在实际切割中声学系统并非与水平方向垂直，而是呈一定的角度，如图6所示，将运动与受力沿声学系统所在坐标系分解，即X、Y、Z坐标系。

图5 超声切割模型

图6 声学系统运动示意图

根据上面的运动判断，超声切割运动分别受到超声冲击力，剪切力及摩擦力等影响，将这多种力沿X，Z方向进行分解分别为FX，FZ。

2.1 Z方向受力分析

Z轴方向的运动包含声学系统在Z方向的振动以及水平方向的进给运动在Z轴上的分量。

由于Z方向本身受到激励的作用，存在受力作用，FZ可以看成是对原来激励的抑制，根据原有运动的变化得到Z方向受力。Z方向的运动轨迹为LZ(t)=Asin(ωt)，故Z方向速度为VZ(t)=Aωcos(ωt)，则加速度为aZ(t)=-Aω2sin(ωt)。Z方向受到的合力为

FZ=moaZ(t)=-ΔAω2mosin(ωt)

(20)

式中:ΔA为Z方向受力之后振幅的减小值;mo为系统等效质量;ω为角频率。

2.2 X方向受力分析

假设系统仅有Z方向振动，而无X方向偏振，则在X轴方向仅有水平方向的进给运动在X的分量，X方向受力仅来自工件。

X方向受力与受力面积S成正比，可表示为

FX=τS

(21)

式中:τ为受力系数。

由于受到超声振动，受力面积S随着上下振动而变化，受力面积S变化规律为

S=Smax-ΔScos(ωt)

(22)

X方向实际受力为

FX=τ[Smax-ΔScos(ωt)]

(23)

2.3 Y方向受力分析

声学系统并没有Y方向的运动，理论上不存在受以上三种力的情况，但由于刀具切割工件时材料存在形变，故刀具在Y方向受到挤压力，挤压力大小与受力面积以及挤压量成正比。

一般情况下，刀具在工件中切割时刀具两个面同时受到挤压力的作用，从而抵消了Y方向的力，但当系统存在以下情况时可能在Y方向力：

(1)切割平台本身跳动；

(2)当存在材料去除的时候，去除面的挤压力小于另一面，此时Y方向存在挤压力；

(3)当材料为各向异性材料时，由于材料的结构属性决定了刀具两侧受力不均。

当切割单边材料去除时，忽略去除边的受力，此时

FY=Sσ1=σ1[Smax-ΔScos(ωt)]=E1ε[Smax-Scos(ωt)]

当切割单边材料不去除，两边的受力不均是由材料的各项异性造成的，由于两边的材料属性不同，材料的弹性模量不同，变形量由刀具厚度确定，两侧挤压量相同，受力面积相同，此时

FY=(E1-E2)ε[Smax-ΔScos(ωt)]

式中:ε为应变，E为弹性模量。

3 声学系统受力实验及分析

通过改变刀具与水平面的倾角θ和切割深度d，对实际超声切割力进行检测，测得的结果见表1。

由表1可知，不同的深度与倾角，各个方向的力也会不同，随着倾角与深度的变化，三个方向的力呈线性变化。X方向的力比Y、Z方向的力更大，同时受力变化也最大，说明X方向为主要受力方向并且加工工艺对X方向力的影响更大。

但由于实际切割时三个方向的力同时存在且同时变化，很难说明哪个方向力对系统的影响更大，故需要对声学系统进行单方向力实验。

采用数显式推拉力计在刀具处对声学系统施加X、Y、Z三个方向的力，考虑到刀具能够承受的受力大小以及实际超声切割时超声切割力不超过20 N，故我们施加力的大小为0～50 N。利用阻抗分析仪对声学系统的参数进行检测。

表1 超声切割力实验结果表

3.1 声学系统受力对系统阻抗值的影响

声学系统在不受任何力的情况下，谐振频率为19 979.0 Hz，阻抗值为240.704 Ω。

由图7所示的声学系统受力与阻抗关系可知，随着三个方向的受力增加，对应的阻抗值都相应的增加，并且三条曲线几乎都是线性增长，说明声学系统受力与阻抗值的增加是成正比的。从增加的幅度来看，X方向受力曲线斜率明显小于Y和Z方向受力曲线，说明该声学系统在Y和Z方向对受力更加敏感。

图7 声学系统受力与阻抗关系图

当受力达50 N时，X、Y、Z三个方向的阻抗值分别达到271.214 Ω，338.075 Ω和329.249 Ω，相较于不受力状态分别增长12.7%，40.5%和36.8%。根据式(19)可知，当超声电源功率一定时，随着阻抗的增加，电流减小，电流的减小会导致振幅减小，最终的结果是导致材料的切割质量降低甚至根本切不动材料。Y、Z方向的阻抗值对受力比X方向更敏感，所以在设计加工工艺设计的时候要尽量减小Y、Z两个方向的受力。

3.2 声学系统受力对系统谐振频率的影响

实验结果如图8所示。

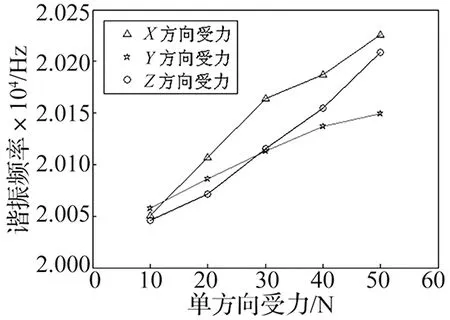
图8 声学系统受力与谐振频率关系图

在三个方向施加力10 N时，系统的谐振频率值几乎相同≈20 050 Hz。但随着受力的增大，系统谐振频率都快速增加，当X、Y、Z三方向分别施加力到50 N时，系统的谐振频率分别为20 226 Hz，20 149.5 Hz，20 209 Hz，虽然增幅的比例不大，但相较与未受力时增加>200 Hz。本声学系统在实际的加工中测量发现，在超声电源没有动态匹配的情况下，如果频率偏移量>100 Hz，此声学系统基本上无法处于正常工作状态，所以200 Hz的偏移量是不满足加工要求的，要避免系统处于高载荷的状态下。

Y方向的谐振频率增加速度明显小于X、Z方向，可知Y方向为谐振频率不敏感方向，这点与阻抗值不同，说明谐振时的阻抗值与谐振频率之间并没有直接的关联。在实际加工中三个方向的力是同时存在的，要保证谐振频率偏移小，不能只是减小单方向的力，而是三个方向的力都要小。

4 结 论

从上述的分析我们可以得出结论：

(1)本文利用一维纵振杆波动方程及压电方程推导出了变幅杆﹑压电陶瓷﹑前端盖四端网络模型，利用四端网络法结合压电换能器﹑变幅杆和负载的输入输出特性建立了超声切割系统整体阻抗模型，从分析的结果看，无论负载的形式是阻值﹑抗值还是阻加抗的形式，都会增加阻抗值的大小。

(2)声学系统在受到三个方向的力之后系统的阻抗值和谐振频率的表现并不相同，系统的阻抗值在Y、Z方向更敏感，而在X方向不敏感；而对于谐振频率，X、Z方向为敏感方向，Y方向为不敏感方向。若系统存在动态匹配的超声电源，则阻抗值作为主要参考指标，其大小直接影响振幅的大小，在无法明显减小受力的情况下，通过控制工艺来减小Y、Z方向的受力而适当增加X方向受力；若系统不存在动态匹配电源，则两个指标须同时考虑，只能通过调整加工工艺参数降低受力或者从根本上设计一套更稳定的声学系统。

(3)本系统在实际应用中发现，频率偏移100 Hz系统就会出现失谐的情况，导致无法工作，阻抗值上升50 N，系统的振幅会无法满足加工要求，由实验图表分析可得，本声学系统在实际加工时，三个方向的力应小于10 N。实验所得的数据能为超声切割加工工艺提供指导。

[ 1 ] 高军，崔巍. 超声切割技术在复合材料加工领域的应用[J]. 航空制造技术,2008(4):50-52. GAO Jun，CUI Wei. Ultrasonic cutting technology applying in the field of composite material processing [J]. Aeronautial Manufacturing Technology,2008(4):50-52.

[ 2 ] 贺西平，高杰. 超声变幅杆设计方法研究[J]. 声学技术, 2006,25(1):82-86. HE Xiping, GAO Jie. A review of ultrasonic solid horn design[J]. Technical Acoustics, 2006,25(1):82-86.

[ 3 ] 黄德中. 超声波振动器四端网络设计[J]. 振动与冲击, 2005,24(5): 110-111. HUANG Dezhong. Design of ultrasonic vibrator using four-end network method[J]. Journal of Vibration And Shock,2005,24(5):110-111.

[ 4 ] 曾凡冲. 超声换能器的设计理论研究[D]. 北京：北方工业大学, 2013.

[ 5 ] 赵福令，冯冬菊，郭东明,等. 超声变幅杆的四端网络法设计[J]. 声学学报, 2002,27(6): 554-558. ZHAO Fuling, FENG Dongju, GUO Dongming,et al. Design of horn using four-endnetwork method[J]. Acta Acustica,2002,27(6):554-558.

[ 6 ] HARADA K, SASAHARA H. Effect of dynamic response and displacement/stress amplitude on oltrasonic vibration cutting[J]. Journal of Materials Processing Technology, 2009,209:4490-4495.

[ 7 ] ZHANG L, DONG J Y, COHEN P H. Material-insensitive feature depth control and machining force reductionby ultrasonic vibration in AFM-Based nanomachining[J]. IEEE Transactions on Nanotechnology, 2013,12(5):743-750.

[ 8 ] STATNIKOV E S, KOROLKOV O V, VITYAZEV V N. Physics and mechanism of ultrasonic impact[J]. Ultrasonics, 2006,44:533-538.

[ 9 ] ZHU X J, WANG J Q, CHENG Q, et al. Research on dynamic grinding force in ultrasonic honing chatter[J]. Key Engineering Material,2011,487:433-437.

[10] 张云电，喻家英，王纯. 珩磨负载对超声珩磨振动系统谐振频率的影响[J].声学学报,1994,14(5):367-371. ZHANG Yundian, YU Jiaying, WANG Chun. Influence of honing load on resonance frequency of ultrasonic honing vibration system[J]. Acta Acustica,1994,14(5):367-371.

[11] 李华，任坤，殷振，等.纵弯转换球面超声振动聚焦系统谐振特性研究[J].振动与冲击,2015,34(6):183-188. LI Hua, REN Kun, YIN Zhen,et al.Resonance features of a new ultrasonic vibration focusing system based on longitudinal-flexural vibration conversion[J].Journal of Vibration and Shock,2015,34(6):183-188.

[12] 赵波，刘折，靳宇晖. 负载对超声加工声学系统特性的影响[J]. 航空精密制造技术, 2012,48(1): 10-13. ZHAO Bo, LIU Zhe,JIN Yuhui. Study on influence of load on acoustic system characteristics of ultrasonic machining[J]. Aviation Precision Manufacturing Technology, 2012,48(1):10-13.

[13] 尹晓春，谢欣平，田阿利. 考虑负载影响的阶梯形超声变幅杆动力特性[J]. 振动与冲击, 2012,31(4): 157-161. YI Xiaochun, XIE Xinping, TIAN Eli. Dynamical performance of ultrasonic stepped horn with consideration of lo ding effect[J]. Journal of Vibration And Shock, 2012,31(4):157-161.

[14] 于伟，阎长罡，李伟. 抗性负载的余弦形复合变幅杆设计及动力学特性研究[J]. 机床与液压, 2011,39(13): 13-16. YU Wei, YAN Changgang, LI Wei. Design and dynamical analysis on a cylindrical and cosine composite horn with reactive load[J]. Machine Tool &Hydraulics,2011,39(13):13-16.

[15] 林书玉，姚文苇.阻性负载超声变幅杆振动特性研究[J]. 声学技术, 2006,25(5): 494-498. LIN Shuyu, YAO Wenwei. Characteristics of ultrasonic horn with resistance load[J]. Technical Acoustics,2006, 25(5):494-498.

Influenceof load on resonance frequency and resonance impedance of an ultrasonic cutting acoustic system

JI Huawei, YU Wenze, HU Xiaoping

(School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, Chna)

An ultrasonic cutting system may have out of harmony, insufficient amplitude, even non-resonance when bearing a load, these lead to serious effects on machining process and machining quality of a workpiece. Here, the impedance and the resonance frequency of a loaded acoustic system were studied. By using the 4-terminal network method, the input / output characteristics of ultrasonic horn, piezoelectric ceramics and end cover were studied, the whole body design equation of an acoustic system was presented, and the impedance, frequency equation and the relationships among load, current and amplitude of the acoustic system were obtained. In order to get influence laws of load on the impedance and resonant frequency of the system, a digital push-pull meter was used to exert a load in a single direction on the acoustic system, the relationships among impedance, resonant frequency and load were tested. The test results showed that the impedance of the system increases after loads are exerted in three directions; with increase in load, the impedance of the ultrasonic cutting system when loads are exerted inYandZdirections increases faster than that does when load is exerted inXdirection; the increments of resonant frequency of the ultrasonic cutting system when loads exerted inXandZdirections are much more than that be when load is exerted inYdirection; the load in the sensitive direction should be reduced in practical application. The results provided a theoretical guidance for the actual processings.

ultrasonic cutting system; load; load model; impedance; resonance frequency

国家自然科学基金(51475130);国防科工局重大专项(A3920133001);浙江省重中之重学科开放基金

2015-10-15 修改稿收到日期：2015-11-26

纪华伟 男，博士，副教授，1976年生

TG663