论二项式定理在高中数学中的应用
2017-01-09王志红
王志红 ●
江西省赣州市于都中学(342300)
论二项式定理在高中数学中的应用
王志红 ●
江西省赣州市于都中学(342300)
二项式定理是高中数学非常重要的部分,也是高中数学的一个难点.体会二项式定理的解题思想,理解二项式定理的概念,并且通过对二项式定理的学习来求解系数求和,以及通项式的求解.本文主要阐述二项式定理的一些基本知识及其相关解题技巧,希望给学生在高中数学解题上带来帮助.
二项式定理;高中数学;二项式系数;赋值法
一、利用二项式定理的概念求解
例1 对任意实数x,如果有x3=a0+a1(x-2)+a2(x-2)2+a3(x-2)3,那么a2的值为( ).
A.3 B.6 C.9 D.12
答案:B.

①项数:共有n+1项;
③每一项的次数是一样的,即为n次,展开式根据a的降幕排列,b的升幕排列进行展开.
二、利用二项式定理的通项求常数项
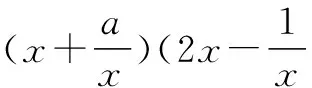
A.-40 B.-20 C.20 D.40
答案:D.
点评 二项展开式中常数项的求解一般是根据二项式的通项的表达式,并让表达式的未知数的指数为零,此时通项中前面的系数即为要求的常数项.
三、赋值法在二项式定理中的应用
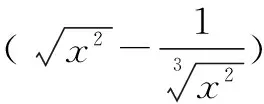
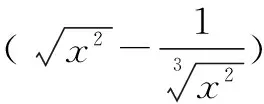
令x=-1,则有a0+a1+…+an=0①,令x=1,则有a0-a1+a2-a3+…+(-1)nan=2n②.
将①-②得:2(a1+a3+a5+…)=-2n,∴a1+a3+a5+…=-2n-1.
由题意得-2n-1=-256=-28,∴n=9.
点评 对于二项式表达式中的a,b取值不固定,因为表达式是一个恒等式,根据这一特点,可以将a,b取一些特定的数,比如-1,0,1,具体的赋值由问题而定.此题将变量取为-1,1再两式相减,在对表达式进行错位相消,从而得到所需要n的数值.
四、利用二项式定理进行近似计算
例4 2015年国内生产总值(DFP)达到676708亿元,比上年增长6.9%.如果“十三·五”期间(2016年~2020年)每年的国内生产总值都按此年增长率增长,那么到“十三·五”末我国国内生产总值约为____.
故填910172亿元.
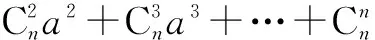
五、利用二项式定理求解余数或整除
例5 求4851除以 7 的余数.
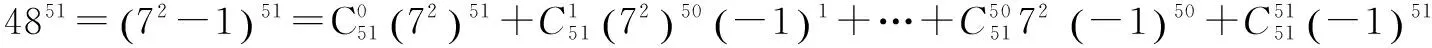
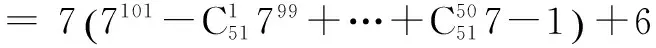
因此,4851除以 7 的余数是6.
点评 利用二项式定理求解余数或整除问题,一定要把除数作为要展开的变量,然后把展开的表达式进行提取公因式.
综上所述,二项式定理是高中数学解题中的一个难点,但也是高考重要的考点,利用好二项式定理这一工具,可帮助中学生解决高中数学许多重要的知识.由于二项式定理让问题化繁为简,所以,中学生务必将二项式定理熟练掌握,将其灵活运用到解题上.本文只是对二项式定理解题进行初步研究,在以后实践教学中还将继续,希望给广大学生学习上带来帮助.
G632
B
1008-0333(2016)34-0030-01
