基于改进记分函数的直觉模糊多维度决策方法

赵宝福，张 超，郭建威（辽宁工程技术大学.工商管理学院；.电信学院，辽宁 葫芦岛125000）

基于改进记分函数的直觉模糊多维度决策方法

赵宝福a，张 超a，郭建威b
（辽宁工程技术大学a.工商管理学院；b.电信学院，辽宁 葫芦岛125000）

针对属性值为直觉模糊值的多决策者、多时间点、多属性及多方案的多维度决策问题，文章基于新的记分函数等决策方法，并讨论了其在企业社会责任评价中的应用。首先，应用TIFHA、MIFHA等算子分别对各时间点和各专家决策进行了集成；其次，应用改进的记分函数对集成后得出的矩阵进行计算，得出记分函数矩阵；再次，运用熵权法算权重；最后引用距离公式及改进的TOPSIS方法将得出的结果进行多属性决策。并针对两家煤炭企业的社会责任履行情况进行了多时点、多专家、多属性决策，通过算例表明了此方法可行且有效。

模糊决策；记分函数；直觉模糊数；算子；多维度

0 引言

由于模糊集能较好地描述事物的模糊本质，自从Zadeh[1]于1965年提出模糊集以来，以模糊集为基础的多属性模糊决策得到了持久、广泛而又深入的研究，针对企业社会责任的模糊决策及评价的研究也屡见不鲜。但Zadeh的模糊集的隶属函数值仅为单一值，只反映是与否的信息。于是Atanassov[2]在Zadeh[1]理论基础上，于1983年进一步发展，提出了直觉模糊集理论。由于它同时包含了隶属度、非隶属度和犹豫度三方面的信息，更能细腻地刻画客观事物的模糊本质，所以，近年来人们对直觉模糊集理论研究产生了浓厚兴趣，并取得丰硕成果。在Atanassov理论基础上，吴冲[3]、闫颖慧[4]、蒙明辉[5]、刘亚丽[6]、周晓辉[7]等人均提出了在各个领域的包含多方案、多属性、多时点、多专家等决策要素中的单个或部分的多属性决策方法，而基于直觉模糊理论的企业社会责任评价的研究成果目前还未见报道。由于模糊理论本身具有不确定性，导致做出的决策可能出现误差，所以有必要依时间点对其进行多次决策，之后将结果集成；同时，考虑多专家决策，可集成多人的智慧，从而使决策结果更加合理准确。此外，还常常需要考虑诸如多属性、多方案等其他因素，以提高决策的准确度。鉴于上述情况，本文基于直觉模糊集理论，首次运用IFHA算子[8]来构造TIFHA算子及MIFHA算子，并构造相应的时间点决策矩阵和多维决策矩阵，从而同时将时间点决策、多专家、多属性、多方案的决策信息进行了多维集成，针对煤炭企业的社会责任履行情况进行了评价比较，使结果的精准度得到极大提高。

1 预备知识

1．1 距离公式[9]

设X={x1,x2,…,xn}为一个有限集合，和为直觉模糊集。则称：

为直觉模糊集A1和A2的距离测度。

1．2 改进的TOPSIS法[10]

设X={A1,A2,…,Am} 是由m个方案组成的方案集，O={o1,o2,…,on}是由n个属性组成的属性集。则方案Ai在属性oj下的评价（属性值）是一个直觉数=(μij,νij),这里 μij和νij分别是方案Ai关于属性oj的满意度（隶属度）和不满意度（非隶属度），其中 μij，νij∈[0 ，1]，且0＜μij+νij＜1，则此决策问题的直觉模糊决策矩阵则模糊比值折中表达式为:

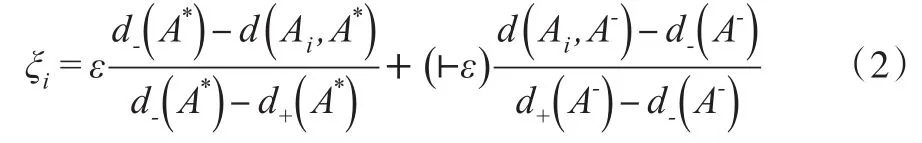
1．3 熵权法[11]

步骤3，计算属性uj输出的信息熵j∈M,当时，规定

步骤4，计算属性权重向量ω＝(ω1,ω2,...,ωn)，其中

2 多维度决策方法

直觉模糊混合平均算子[8]：

直觉模糊混合平均算子的另一种表现形式[8]：

定义2，设α(t1),α(t2),…,α(tq)为q个不同时间点tk(k=1,2,…,q)的直觉模糊数，且ω(t)=(ω(t1),ω(t2),…,ω,(tq))T为时间点序列{tk（}k=1,2,…,q)的权重向量，ω(tk)≥0则称：为累积时间点直觉模糊混合平均（TIFHA）算子。

根据式（4）IFHA算子的定义，式（5）可写为：

利用TIFHA算子，可得：

定义3：设决策者Vi∈V,i=1,2,…,n,V是所有参与决策的专家全体的集合，即决策群体集，Vi代表第i个决策者，wj代表属性uj(j=1,2,…,m)的权重。Yl∈Y,l=1,2,…,p。Y为方案全体的集合，Yl代表第l个方案。

则称：

为多维直觉模糊混合平均(MIFHA)算子。 用(MIFHA)算子求得每个专家决策Vj的各属性uj(j=1,2,…，m)的综合属性值。将得到的用直觉模糊决策矩阵

表示。称矩阵E为直觉模糊混合平均(MIFHA)算子的多维决策矩阵。

定义4：设决策者Vs∈V(s=1,2,…,l),V是所有参与决策的专家全体的集合，即决策群体集，Vs代表第s个决策者，Vs在方案Yi(i=1,2,...,n)及属性uj（j=1,2,...,m）下，直觉模糊决策值为弃权部分为则记为精确记分函数。其中：

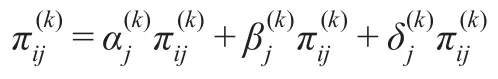
定理1：设决策者Vs∈V(s=1,2,…，l),V是所有参与决策的专家全体的集合，即决策群体集，Vs代表第s个决策者，Vs在方案Yi(i=1,2,...,n及属性uj(j =1,2,...,m )下直觉模糊决策值为弃权部分为（其中精确记分函数满足：

又因为

具体步骤：

（2）分别用TIFHA算子对p个企业的信息进行集成，得到p个D矩阵,记为Dl,(l=1,2,…,p)。

（3）分别用MIFHA算子对各个企业的D矩阵进行集成各得到一个对企业各属性进行决策的1行j列的D.矩阵共p个，记为D.l(l=1,2,…,p)。之后将p个矩阵D.l合并，得到直觉模糊混合平均(MIFHA)算子的多维决策矩阵E。

（4）用得分函数式（9），对E的每一个直觉模糊数进行计算，得到一个得分函数值矩阵E.。

（5）用熵权法计算E.的权重。

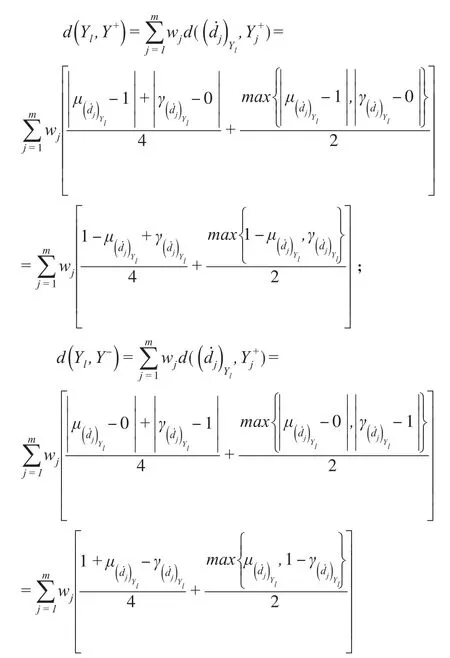
（6）分别计算出D.l的正理想点和负理想点。分别定义为直觉模糊正理想点和直觉模糊负理想点，其中为 m个最大的直觉模糊数，且为m个最小的直觉模糊数。为方便描述，把方案记为之后运用式（1）分别计算各方案与正理想点和负理想点的距离,权重采用第4步得到的权重，并用式（2）计算并排序以对两个企业的总体情况进行比较。其中：

（7）方法可以将多于两个的多个企业之间进行企业社会责任履行情况的比较，具有较强的实用性，同时本方法简单易行。

3 算例分析

举一个简单的算例。由两位来自企业管理决策领域的专家（决策者）(νi,i=1,2)组成的专家组利用三个企业社会责任评估指标（即属性，为了说明本方法仅列了三个属性）(uj,j=1,2,3)对两个煤炭企业(Yl,l=1,2),分别从时间点t1,t2建立时间点矩阵 D1(t1)、D1(t2)、D2(t1)和D2(t2)，以对社会责任履行情况进行评估比较。专家分别用直觉模糊数描述各煤炭企业在企业社会责任评价指标下的特征。

（1）建立各企业的决策矩阵。

第一个企业的t1时间的决策矩阵D1() t1如表1所示。

表1 直觉模糊时间点矩阵D1(t1)

第一个企业的t2时间的决策矩阵D1(t2)如表2所示。

表2 直觉模糊时间点矩阵D1(t2)

第二个企业的t1时间的决策矩阵D2(t1)如表3所示。

表3 直觉模糊时间点矩阵D2(t1)

第二个企业的t2时间的决策矩阵D2(t2)如表4所示。

表4 直觉模糊时间点矩阵D2(t2)

（2）用TIFHA算子计算，得到决策矩阵D1（保留小数点后一位小数），如表5所示。

表5 直觉模糊决策矩阵D1

表6 直觉模糊决策矩阵

表6 直觉模糊决策矩阵

ν u1（0.5，0.1）u2（0.7，0.1）u3（0.8，0.1）

表7 直觉模糊决策矩阵

表7 直觉模糊决策矩阵

ν u1（0.8，0.1）u2（0.6，0.1）u3（0.5，0.2）

于是，得到矩阵E如表8所示。

表8 直觉模糊矩阵E

表9 得分值矩阵

表9 得分值矩阵

Y1 Y2 u1 0.6 0.7 u2 0.7 0.6 u3 0.7 0.4

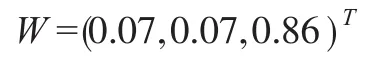
⑹利用公式计算得到：

取ε=0.5，则ξ1=1，ξ2=0，ξ1＞ξ2，所以第一个企业的社会责任总体履行情况要优于第二个企业。

4 结论

为了更准确地测度企业社会责任评价指标的模糊程度，本文提出了基于直觉模糊理论及算子理论的新评价决策方法。由于它同时包括了决策的隶属度信息、非隶属度的信息及决策的犹豫度信息，从而可更好地描画不确定程度。在此基础上，集成了多方案、多专家、多时点、多属性的评价要素，提出了多维矩阵的概念等一系列计算方法及一些性质、定理，避免了片面地从某一方面进行决策而可能导致的误差，从而有效地增加企业社会责任评价的精准度。从算例可知本文所提出的方法不仅可行而且有效。本文所提出的方法也可应用到诸如厂址选择、投资项目选择、人才评定、职工绩效考核、人员调动、虚拟企业伙伴选择等多属性决策问题中，具有较好的理论价值和实际应用价值。

[1]Zadeh L A.Fuzzy sets[J].Information and Control,1965,(8).

[2]Atanassov K.Intuitionistic Fuzzy Sets[J].Fuzzy Sets&Systems,1986,20 (1).

[3]吴冲,万翔宇.基于改进熵权法的区间直觉模糊TOPSIS方法[J].运筹与管理,2014,(5).

[4]闫颖慧,祖璇.基于相对熵的区间型直觉模糊集多属性决策方法[J].佳木斯大学学报(自然科学版),2015,(1).

[5]蒙明辉,裴向军,吴梦秋.基于模糊多属性群决策的危岩稳定性影响因子筛选研究[J].路基工程,2015,(1).

[6]刘亚丽,张元鑫,李红波.项目投资决策信息不完全直觉模糊的TOPSIS法[J].昆明理工大学学报(自然科学版),2015,(1).

[7]周晓辉,姚俭,吴天魁.基于新型区间直觉三角模糊熵的多属性决策方法[J].数学理论与应用,2013,(4).

[8]Xu Z.Intuitionistic Fuzzy Aggregation Operators.[J].IEEET.Fuzzy Systems,2007,(15).

[9]Wang W,Xin X.Distance Measure Between Intuitionistic Fuzzy Sets [J].Pattern Recognition Letters,2005,26(13).

[10]刘满凤,任海平.基于一类新的直觉模糊熵的多属性决策方法研究[J].系统工程理论与实践，2015,(5).

[11]Hwang H L,Yoon Y.Multiple Attribute Decision Making and Appli⁃cations[M].New York:Springer-Verlag,1981.

[12]张肃.基于记分函数的直觉模糊多属性群决策方法[J].统计与决策,2015,(7).

[13]高建伟，刘慧晖，谷云东.基于前景理论的区间直觉模糊多准则决策方法[J].系统工程理论与实践,2014,(12).

（责任编辑/浩 天）

F224.9

A

1002-6487（2016）24-0054-05

赵宝福（1957—），男，辽宁昌图人，教授，博士生导师，研究方向：企业管理、产业管理资源与配置。张 超（1983—），男，辽宁阜新人，博士，经济师，研究方向：企业管理、战略与创新。