多状态系统预防性维修组合模型

张 斌，张 莹，刁海涛，张婧怡（南京信息工程大学 数学与统计学院，南京 210044）

多状态系统预防性维修组合模型

张 斌，张 莹，刁海涛，张婧怡
（南京信息工程大学 数学与统计学院，南京 210044）

文章研究了两部件系统的预防性维修组合问题。根据子系统正常与否，将系统分为四个不同的运行状态。当单个子系统发生故障时，系统能够继续工作，但单位时间的收益将发生变化。定期对子系统进行预防性维修，可以减小子系统的故障率。构建了状态转移方程，并求出各状态的稳态概率。综合考虑了单位产品的获利、减产的损失、不合格品的损失、故障维修费用和预防性维修费用等，以有效生产率满足阈值为约束条件，以单位时间净收益最大为目标，提出预防性维修组合优化模型。分析了模型参数对预防性维修决策的影响。

多状态；马尔可夫过程；维修组合

0 引言

许多实际系统通常包括多个子系统。在使用过程中，如果对系统的维修不足，可能导致突发性故障频发，从而造成巨大的经济损失；如果对系统的维修过度，又将使维修费用过高，甚至维修费用超过系统本身的成本很多倍。因此，在故障前对系统进行预防性维修及预防性维修决策的优化非常重要。

根据系统运行情况的不同可以将系统分为多个运行状态。Lad和Kulkarni(2010)[1]根据故障的影响对系统的状态进行了分类。Liu和Huang(2010)[2]利用半更新过程描述一个多状态系统的每个单元在维修后的运行情况，进而提出最优预防性维修方案。Sheu等(2012)[3]考虑了系统存在两类故障，通过引入故障率函数改进因子提出不完全预防性维修模型。Attia和Abou Elela等(2011)[4]针对存在正常运行、异常运行和故障三个状态的系统，在假定故障率是预防性维修次数函数的基础上，提出不同状态下预防性维修策略的优化模型，但仅考虑了单部件系统的维修问题。本文将文献[4]提出的故障率是预防性维修次数函数的思想由单部件系统推广到两部件系统，根据子系统的运行情况将系统分为正常运行、系统运转但生产率降低、生产率不变但过程失控和停止运行四个状态。根据状态转移规律，构建了状态方程。在单位时间平均净收益最大的前提下，以有效生产率满足阈值为条件，提出了多状态系统的预防性维修组合模型。本文所提方法可以为两部件系统的预防性维修组合提供决策依据。

1 四状态系统模型

假设某系统由两个独立的子系统并联组成，每个子系统有两种工作状态：正常状态和故障状态。根据子系统正常与否，可以将系统的运行状态分为四种：

状态0：两个子系统都正常，系统处于完全正常状态；

状态1：子系统2正常，但子系统1故障，系统处于不完全正常状态1；

状态2：子系统1正常，但子系统2故障，系统处于不完全正常状态2；

状态3：两个子系统都故障，系统处于完全故障状态。

当单个子系统发生故障时，系统能够继续工作，即系统处于状态1或状态2时可以继续运行。子系统i(i=1，2)发生故障的时间和维修时间服从指数分布，子系统i(i=1，2)的故障率为λi，维修率为μi。当系统处于状态1或状态2时，经过维修可以使系统修复到初始状态，即“修旧如新”。子系统的故障事件互不影响，且在极短的时间内不会出现两个子系统同时故障的情况。当系统处于状态3时，系统停止运行，通过维修可将其修复到初始状态，维修率为μ。系统在状态 j(j=1，2，3)下的维修时间就是系统在该状态的逗留时间。系统的状态转移如图1所示。

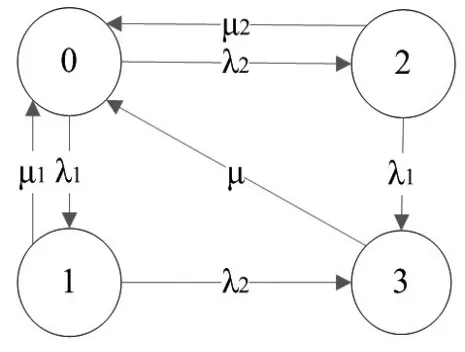
图1系统的状态转移图

2 状态方程及稳态概率

为了计算系统在稳态下处于状态 j(j=0，1，2，3)的概率Pj，先考虑转移概率Pij(t+Δt)，其中Δt＞0。由柯尔莫哥洛夫-切普曼公式，得则：

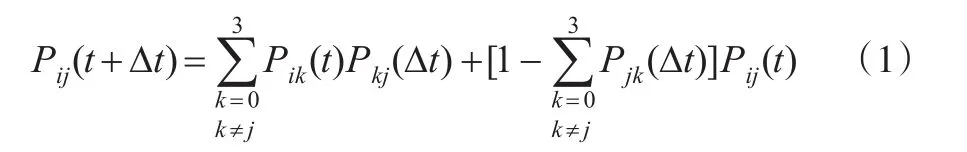
已知系统在0时刻处于状态0，即：

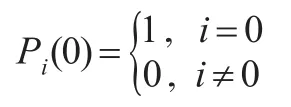
由于系统在初始时刻的状态是0为已知，故将Pij(t)简记为Pj(t)。在Δt很小的情况下，可以得到该马尔可夫过程的转移概率为：

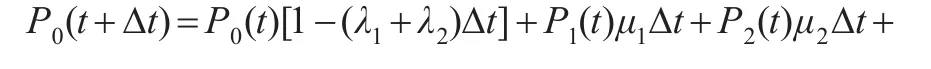
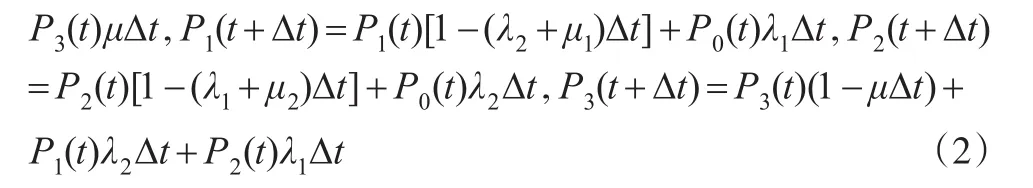
式（2）方程两边对Δt=0求导，得状态微分方程为：

由于系统的任何一个状态只能从其他状态转换得来，因此，该过程是一个不可复归的马尔可夫过程，其稳态概率存在。由及，得各状态的稳态概率满足方程：

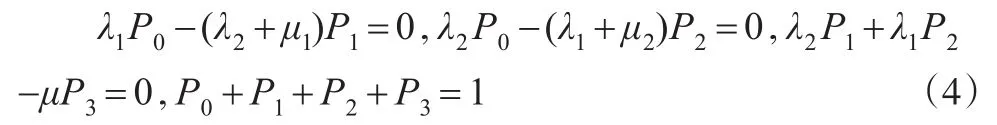
由式(4)解得各状态的稳态概率为：

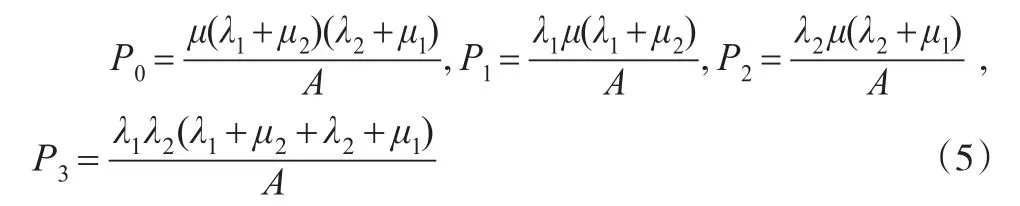
其中，A=λ1(λ1+μ2)(λ2+μ)+λ2(λ1+μ)(λ2+μ1)+μ(λ1+μ2) (λ2+μ1)系统在稳态时的可用度为：

可用度是系统能工作时间与能工作时间、不能工作时间的和之比，是系统的可用性参数。对于一个多状态系统，如果系统所处状态不同，产生的收益也不同，仅考虑可用度或将可用度作为目标函数来制定预防性维修方案并不合理。实际生产中，系统的有效生产率往往比可用度更加受关注。为此，本文将有效生产率满足阈值作为约束条件，以系统的单位时间平均净收益为目标函数来确定最优预防性维修方案。

3 预防性维修组合模型

3．1 模型假设

为了构建预防性维修组合模型，对系统作如下假设：

（1）系统在正常状态下的生产率为R(单位时间内生产的产品数)，过程能力指数Cp=Cpk=1，即过程输出无偏且规范限在±3σ处，其中σ为质量特性的标准差。在状态1下，系统能够继续运行，但生产率减小到r=αR(0＜α＜1)。在状态2下，系统输出的生产率不变，但过程处于失控状态，过程输出质量特性的均值漂移δσ。此时，生产不合格产品的比率将增多。

（2）正常状态下生产一件产品的平均获利为d，产量减少一件的损失为Clp，过程失控时生产一件不合格产品的损失为d1。

（3）为了减小系统故障的发生率，定期对子系统进行预防性维修。预防性维修分为完全预防性维修和不完全预防性维修。不完全预防性维修的作用通常分为减小实际年龄和减小故障率。本文假定预防性维修不能使系统完全修复，但随着预防性维修次数的增加系统的故障率将降低，即故障率是预防性维修次数的函数，λi=λi(ni)，i=1，2，其中，ni为子系统i在单位时间内的预防性维修次数。

（4）系统在故障状态1、状态2、状态3下单位时间的故障维修费用分别为CCM1、CCM2、CCM3。对子系统i(i=1，2)进行一次预防性维修的费用为CPMi(i=1，2)，预防性维修不影响系统工作且维修时间可以忽略不计。

（5）系统的各类故障能够被及时发现，并立即维修。系统在故障状态1或状态2下的运行时间等于对状态1或状态2的维修时间。

3．2 维修组合模型构建

系统在使用期内单位时间平均净收益等于系统在各状态下的收益减去预防性维修费用，即目标函数为：

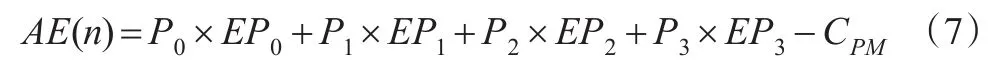
其中，EPj(j=0，1，2，3)为系统处于状态 j时单位时间的收益，R1为系统的平均有效生产率，p(0＜p＜1)为生产任务完成率的阈值。

本文的目标是在满足约束条件的前提下，寻找单位时间内对子系统进行预防性维修的次数ni(i=1，2)，使单位时间平均净收益AE(n)最大。

系统处于状态0时，工作正常。在该状态下，单位时间的收益等于生产率乘以单位产品的收益，即EP0=R×d。系统处于状态1时单位时间的收益等于生产产品的收益减去产量减少的损失再减去故障维修费用，即：

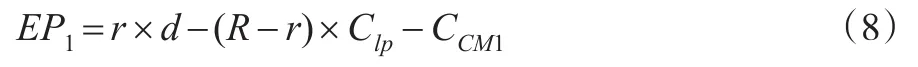
同理，系统处于状态2时，单位时间的收益等于生产有效产品的收益减去有效产品减少的损失再减去不合格品损失和故障维修费用，即：

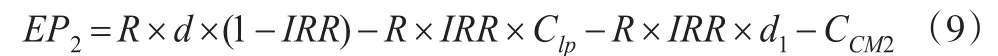
其中，IRR为系统处于状态2时的不合格品率。

在状态2下产品的不合格品率为：

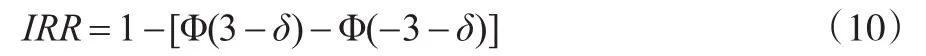
系统在状态3下将停止运行，此时立即对系统进行故障维修。因此，系统在该状态下单位时间的收益为负值，等于停机减产的损失与故障维修费用的和：

系统处于状态0、状态1和状态2时的有效生产率分别为R、r和R×(1-IRR)。因此，系统的平均有效生产率为：

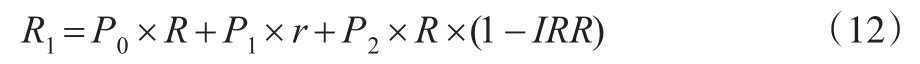
系统在单位时间内的预防性维修费用等于对子系统进行一次预防性维修的费用乘以预防性维修次数，即：

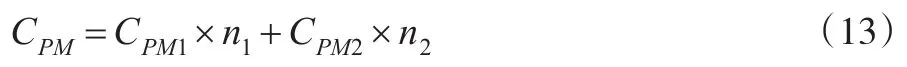
如果不考虑对子系统进行预防性维修，则系统在使用期内单位时间平均净收益为：

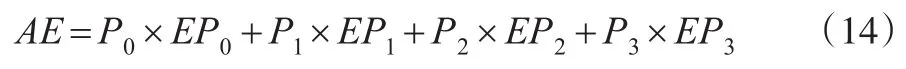
4 数值分析

考虑某系统是由两个独立的子系统并联而成，两个子系统的故障率与预防性维修次数的关系分别为[10]：λ1(n1)=其中r1=1，r2=1.5。两个子系统的维修率分别为：μ1=5，μ2=5。

系统在正常状态下的生产率R=1000，单位产品获利d=30。当子系统1发生故障时，生产率是正常状态下的0.9倍，即α=0.9，产量减少单位产品的损失Clp=10。系统的实际平均有效生产率不得低于正常状态下的0.99倍，即生产任务完成率的阈值p=0.99。当子系统2发生故障时，生产率不发生变化，但过程处于失控状态，过程均值漂移δσ，其中δ=0.75。失控状态生产单位不合格品的损失d1=20。系统处于故障状态1、状态2、状态3时单位时间维修费用分别为：CCM1=50，CCM2=60，CCM3=100。对两个子系统进行一次预防性维修费用分别为：CPM1=10，CPM2=10。

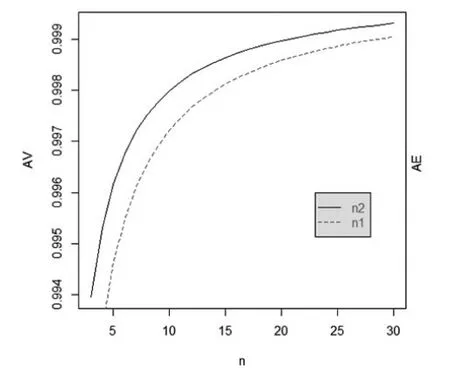
图2系统可用度与预防性维修次数的关系

根据式（6），系统的可用度与预防性维修次数的关系如图2所示，由图知当n1、n2增大时，可用度AV将增大。

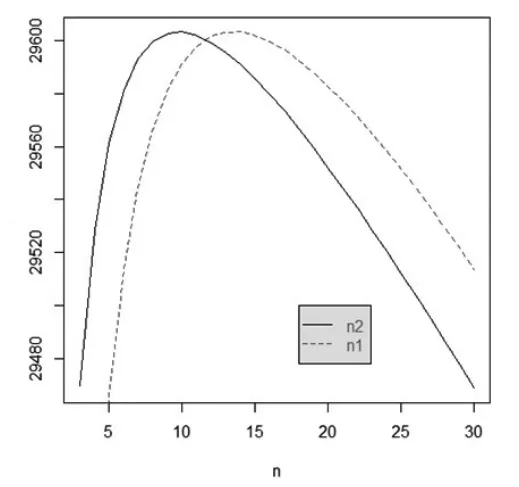
图3单位时间平均净收益与预防性维修次数的关系

根据式（7），单位时间平均净收益与预防性维修次数的关系如图3所示，当n1、n2增大时，单位时间平均净收益AE(n)先增大然后减小，在n1=14，n2=10时，单位时间平均净收益AE(n)达到最大值29603.27。此时，系统的可用度AV=0.9980，生产任务完成率

如果不考虑对子系统进行预防性维修，则由式（14）得，单位时间平均净收益 AE=23637.03，系统的可用度AV=0.8538，生产任务完成率R1/R=0.8426。利用本文模型可以使单位时间平均净收益增大的比例为×100%=25.24%。同时，系统的可用度和生产任务完成率都将得到大幅度提高。

为了分析子系统故障造成的后果对决策变量的影响，下面分别讨论子系统1故障时的生产率和子系统2故障时的均值漂移与最优预防性维修策略、净收益率、可用度及生产任务完成率之间的关系。具体见表1和表2。

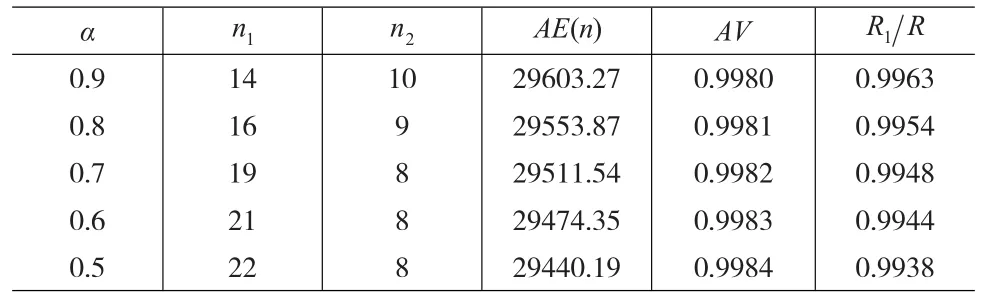
表1 α对预防性维修策略、净收益率、可用度及生产任务完成率的影响

由表1知，在系统处于状态1时，随着生产率的降低，n1将增大，n2减小，单位时间平均净收益AE(n)减小，系统的可用度AV增大，生产任务完成率减小。

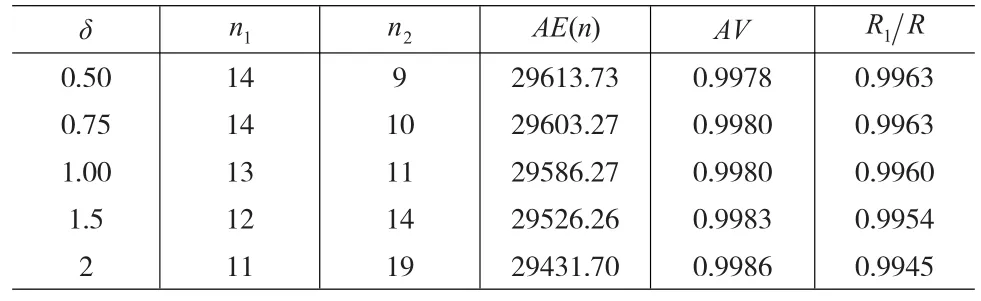
表2 δ对预防性维修策略、净收益率、可用度及生产完成率的影响

由表2知，在系统处于状态2时，随着过程均值漂移率的增加，n1将减小，n2增大，单位时间平均净收益AE(n)减小，系统的可用度AV增大，生产任务完成率减小。

5 总结

本文讨论了存在四种状态的两部件并联系统的预防性维修组合问题。假定两个子系统的故障对系统的影响分别是降低生产率和增大不合格品率，故障时间和维修时间相互独立且服从指数分布，利用柯尔莫哥洛夫-切普曼公式构建状态微分方程。考虑到系统在不同状态下运行的收益不同，本文将有效生产率满足阈值作为约束条件，在综合维修成本和相关损失的基础上，提出两部件多状态系统预防性维修优化模型。数值分析验证了所提模型的有效性，模型参数对最优预防性维修方案影响的分析表明：

（1）在系统处于状态1时的生产率越低，对子系统1的预防性维修次数越大，子系统2的预防性维修次数越小，但生产率的改变对子系统1预防性维修次数的影响较大；

（2）统处于状态2时的均值漂移越大，即不合格品率越大，对子系统1的预防性维修次数越小，子系统2的预防性维修次数越大，但均值漂移对子系统2预防性维修次数的影响较大；

（3）系统的生产率降低或产品不合格率增大，系统的可用度增大，但生产任务完成率却减小。表明对于多状态系统，当系统在不同状态下运行的收益不同时，仅关注可用度是不够的。

[1]Lad B K,Kulkarni M S.An Expert Based Methodology for Cost Orient⁃ed Analysis of Machine Tool Reliability[J].International Journal of Performability Engineering,2010,6(2).

[2]Liu Y,Huang H Z.Optimal Replacement Policy for Multi-State Sys⁃tem Under Imperfect Maintenance[J].IEEE Transactions on Reliabili⁃ty,2010,59(3).

[3]Sheu S H,Chang C C,Chen Y L.An Extended Sequential Imperfect Preventive Maintenance Model With Improvement Factors[J].Commu⁃nications in Statistics:Theory and Methods,2012,41(7).

[4]Attia A F,Abou Elela E D,Hosham H A.The Optimal Preventive Maintenance Policy for the Multistate System Profit[J].Communica⁃tions in Statistics:Theory and Methods,2011,40(23).

（责任编辑/易永生）

O213.1

A

1002-6487（2016）24-0179-04

江苏省大学生实践创新训练计划项目（001266）