O型钢丝绳隔振器的三向动态特性*

2017-01-09王红霞龚宪生葛建兵

振动、测试与诊断 2016年6期

关键词：O型钢丝绳幅值

王红霞，龚宪生，潘飞，葛建兵

(1.重庆大学机械传动国家重点实验室重庆 ,400044)(2.湖北汽车工业学院机械工程学院十堰 ,442002)

O型钢丝绳隔振器的三向动态特性*

王红霞1,2，龚宪生1，潘飞1，葛建兵1

(1.重庆大学机械传动国家重点实验室重庆 ,400044)(2.湖北汽车工业学院机械工程学院十堰 ,442002)

采用周期动态加载试验方法,分别获得了O型钢丝绳隔振器在剪切、横滚和拉压方向上随激励振幅和频率变化的动态迟滞特性。在剪切和横滚方向，试验迟滞环呈现对称特性；在拉压方向上，试验迟滞环呈现非对称迟滞特性，并随着激励幅值的增加，迟滞环面积增大而且非对称迟滞特性表现的更加明显；在拉伸方向上拥有硬化刚度；压缩方向上刚度明显软化。在测试频率段，隔振器3个承载方向的滞回性能与频率无关。针对隔振器的三向动态特性，提出一种改进的归一化Bouc-Wen模型和一种简单有效的参数识别方法，并基于试验数据验证该模型和参数识别方法的有效性。结果表明，试验曲线和理论模型预测曲线吻合较好，该模型和方法能够分别有效描述隔振器的三向动态特性。

O型钢丝绳隔振器; 迟滞特性; 参数识别; 归一化Bouc-Wen模型

引言

钢丝绳隔振器是一种典型的非线性阻尼迟滞隔振装置，具有良好的干摩擦高阻尼特性，可以承受剪切、横滚和拉压载荷。广泛应用于工业、国防设备、车辆及船舶等领域[1-5]。传统的钢丝绳隔振器类型有T型(螺旋型，即条型)、G型(拱型)和Q型(球型)3种结构[6]。钢丝绳的装夹、大螺旋定型，均需要通过专用工装完成，而且钢丝绳隔振器一旦成型，其弹性阻尼特性即在一定范围内确定，而且损坏后不易维修，只有更换。鉴于目前钢丝绳隔振器的结构形式在制造和使用过程中的问题，笔者提出了一种新的O型钢丝绳隔振器，弹性阻尼元件采用彼此独立的钢丝绳绳圈。该隔振器结构简单，绳圈装夹更换方便，组装灵活，使用寿命长。由于钢丝绳结构的复杂性，理论上尚没有建立关于隔振器结构参数和振动水平的精确物理模型。然而,在许多工程应用中，针对非线性迟滞系统的建模和参数识别方法的研究却一直没有停止[7-14]。它们主要用于描述对称迟滞特性，不能准确描述该隔振器拉压方向的非对称迟滞响应特性。Ni 等提出的模型[15]可以准确地描述钢丝绳隔振器在剪切、横滚和拉压方向上的动态迟滞特性，但是采用其模型对该隔振器进行参数识别时，寻找合适的初始参数非常困难。本研究中首先采用试验方法来研究隔振器在剪切、横滚和拉压方向上随激励振幅和频率变化的动态特性；然后，针对其动态特性，提出一种改进的归一化Bouc-Wen模型，并采用一种简单有效的两阶段识别方法对模型的相应参数进行识别；最后，对该模型和方法进行有效性验证。

1 试验研究

1.1 试验方案设计

为了充分了解O型钢丝绳隔振器的动态特性，首先采用试验方法来研究激励振幅A和频率f在剪切、横滚和拉压方向上对动态特性的影响。钢丝绳圈中径为D，钢丝绳直径为d。该实验采用D为63 mm，绳圈个数为8,d为5 mm的钢丝绳环弹性阻尼元件组成的O形钢丝绳隔振器。分别取激励信号幅值A范围为1～10 mm，频率f为3Hz,以及激励幅值为2 mm，频率范围为1～19Hz(奇数频率)分别在剪切、横滚和拉压方向上开展动态特性试验。

1.2 试验装置

试验装置如图1所示。试验是在弹性体试验台(mechanical testing & simulation,简称MTS)弹性元件测试系统(型号831)试验机上采用位移激励方式对隔振器动态特性进行试验研究。隔振器上夹具通过螺纹转接头1与MTS上夹具相连， MTS上夹具与振动台体相连，位移传感器内置于MTS上端。隔振器下夹具1，2通过螺纹转接头2与MTS下夹具相连，MTS下夹具与地基相连。同时采集力和位移传感器信号传输至计算机进行数据处理。

1.3 试验结果分析

为了研究各参数对隔振器动态特性的影响，从众多试验数据中挑选部分代表性的工况进行分析，分析结果如下。

1.3.1 频率对隔振器动态性能的影响

图2是隔振器在激励幅值为2 mm、频率为1～19 Hz(奇数频率)剪切、横滚和拉压方向上的试验迟滞环。由图可知，在测试频率段，频率对隔振器3个承载方向的滞回性能影响不大，这与以往的研究相吻合[14 -15]。

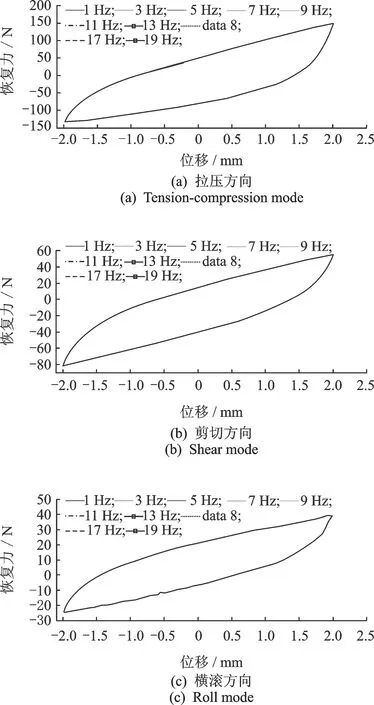
图2 频率不同的试验迟滞环Fig.2 The hysteresis loops of different frequency

1.3.2 振幅对隔振器动态特性的影响

图3 幅值不同的试验迟滞环Fig.3 The hysteresis loops of different amplitude

图3是隔振器在幅值范围1～10 mm，频率为3 Hz，在剪切、横滚和拉压方向上的试验数据经过低通滤波后的稳态试验迟滞环。其中，在剪切和横滚方向上为了避免偏载的影响，采用两个同型号的隔振器并联在一起，如图1(c，d)所示，因此在分析单个隔振器时，恢复力要除以2进行研究。从振动测试的结果看，该隔振器的动态特性和激励幅值相关性较大。在剪切和横滚方向，由于结构对称，迟滞环是对称的,而且隔振器在这些方向上与动态迟滞环非常接近。在拉压方向上，随着激励幅值的增加阻尼增大，而且非对称迟滞特性表现的更加明显。加载时包含一段硬化重叠曲线，卸载时刚度变化比较明显。拉伸方向上拥有硬化刚度，压缩方向上刚度明显软化。这与文献[15]关于T型(螺旋型)钢丝绳隔振器三向动态特性研究相吻合。

1.3.3 能量耗散特性

非线性迟滞阻尼特性取决于一个周期试验迟滞环的面积，也就是每个动态稳定周期耗散的能量。试验结果已经证明了迟滞阻尼特性与频率无关，因此这部分主要研究激励振幅对迟滞环面积的影响。研究结果如图4所示。

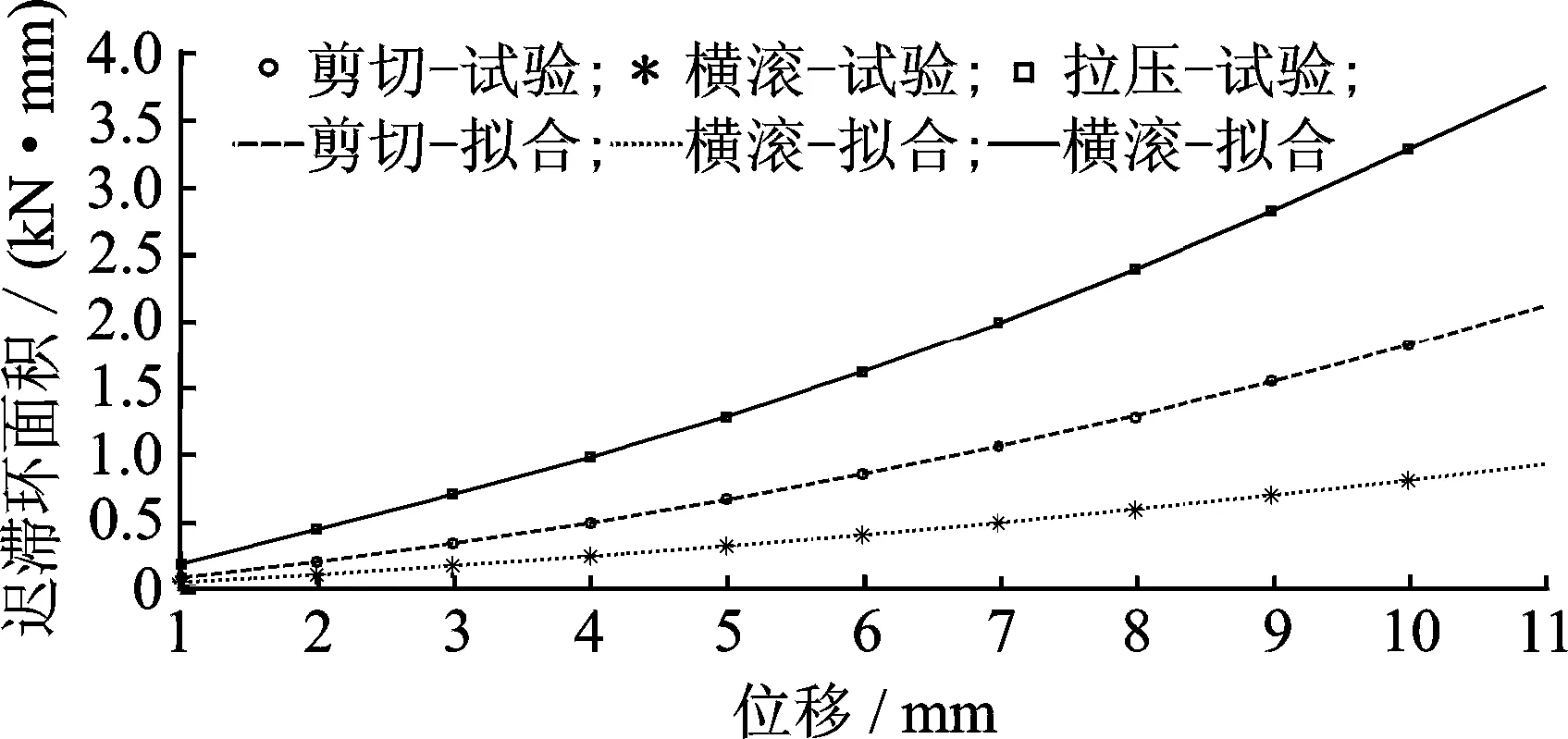
图4 预测和试验迟滞环面积比较图Fig.4 Comparison of the predicted and experimental hysteresis loops areas

由图4可知，隔振器迟滞环面积受激励振幅的影响很大，它随着振幅的变大而迅速弱线性增大，清晰地反映出激励振幅对迟滞耗散能量的决定性影响。剪切和横滚方向的能量耗散明显小于拉压方向，说明该隔振器拉压方向的动态性能优于其他两个方向，是应用中的主要承载方向。横滚方向能量耗散最小，应尽量避免隔振器在该方向工作。然后，根据3个方向迟滞环面积随激励幅值的变化规律，利用Matlab中的cftool工具采用多项式进行非线性拟合，拉压、横滚和剪切方向拟合公式分别如下Sv= -0.149 2A4+3.764A3-17.7A2+

286.5A-106.9

(1)

Sr=3.566A2+44.62A-14.65

(2)

Ss=0.241 9A3+5.684A2+103.5A-46.2

(3)

其中：Sv，Sr和Ss分别为拉压、剪切和横滚方向试验迟滞环的面积；A为输入位移幅值。

为了评估拟合结果的精确性，分别计算三向预测曲线的均方根误差(RMSE)，见表1，RMSE值越小说明拟合越精确。

表1 拟合曲线的拟合度指标RMSE

2 建模和参数辨识

2.1 O型钢丝绳隔振器迟滞模型

根据图3隔振器的试验迟滞曲线，在垂向承受拉压载荷时，隔振器呈现出非对称迟滞特性，在剪切和横滚方向时呈现出对称迟滞特性。该隔振器具有有界输入输出(bounded input-bounded output,简称BIBO)和能量耗散特性，为了获得非对称迟滞环，对文献[12]提出的归一化Bouc-Wen模型进行改进，表述如下

(4)

(5)

其中：ω为纯迟滞恢复力； Φ为输出恢复力；x为输入激励位移；kx,kω,ρ,σ,n为模型参数。

该模型主要用于描述对称迟滞特性，不能准确描述隔振器垂向动态迟滞特性，因此，在该模型基础上引进了两个多项式因子对模型进行修正以满足对该隔振器动态特性的描述，具体模型为

(6)

(7)

该模型中的恢复力包括非线性弹性恢复力Fe、非线性放大因子Fn和纯迟滞恢复力ω。Fe和Fn分别用阶数N和M的多项式表示，kei和knj分别是非线性弹性恢复力Fe和非线性放大因子Fn的多项式系数。另外，该模型是一个与频率无关的改进的归一化Bouc-Wen模型，可以对试验频率为1～19Hz(奇数频率)的O型钢丝绳隔振器试验迟滞环进行建模。为了更好地应用这个模型对O型钢丝绳隔振器动态特性进行描述，必须要对模型参数进行识别。

2.2 O型钢丝绳隔振器模型参数识别

为了获得模型参数，最常用的方法是建立非线性最小二乘法的优化方程

minf(kei,knj,ρ,σ,n)=‖ΦP(t)-Φe(t)‖

(8)

其中：ΦP(t)和Φe(t)分别为模型预测响应和试验测试响应值。

求解以上优化方程会涉及到非线性迭代算法，而且每一步迭代中均要计算方程(7)，并要选取初始值，很容易出现无法收敛的情况。因此针对式(6)和式(7)采用分阶段识别方法，基于试验数据进行模型参数辨识。第一阶段采用线性最小二乘法识别非线性弹性恢复力Fe和非线性放大因子Fn的相关参数kei和knj；第二阶段采用极限环法求得迟滞模型参数ρ,σ和n。

2.2.1Fe和Fn相关参数的识别

由图3可知，对于幅值较大的试验迟滞环，纯迟滞恢复力ω是有界的。在拉压方向采用幅值为7 mm、频率为5 Hz的试验迟滞环作为待识别的模型参数的试验数据，如图5所示。为了参数识别的需要，假定在稳定段ω≡1，则在稳定段恢复力表示为

(9)

其中:Φl，Φu分别为O型钢丝绳隔振器在稳定段的加载和卸载时的迟滞恢复力。

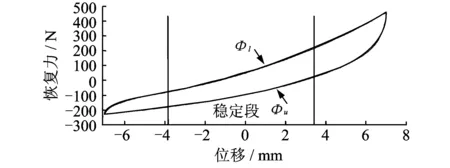
图5 待识别参数的试验迟滞环Fig.5 The tested hysteresis loop for identification of model parameters

由式(9)可以求得

(10)

(11)

由于采集的试验数据是离散的，式(10)写成离散形式为

(12)

其中：下角标k为离散试验数据第k个点，k取值为1，2，…，K，K为试验数据的长度。

先识别Fe的相关参数，由式(6)和式(12)可以得到

(13)

其中：ke= [ke1,ke2, …,keN]为非线性刚度系数矢量；yN为非线性弹性恢复力的线性化变形矩阵。

(14)

为了求得非线性刚度系数ke，对应的线性最小二乘法的优化方程为

(15)

采用线性最小二乘法[16]求解式(15)，从而求得非线性刚度系数[ke1,ke2, …,keN]。Fn的相关参数kn的识别，采用同样的方法求得放大系数 [kn1,kn2, …,knM]。

2.2.2 迟滞参数的识别

为了识别迟滞参数，必须从试验数据中提取纯迟滞响应ω。根据第一阶段参数识别结果以及式(6)可以得到ω的表达式，写成离散形式为

(16)

其中：Φk为试验迟滞环恢复力的第k个试验数据点；yN,k和yM,k分别表示矩阵yN和yM中的第k列。

式(7)可以写成如下形式

(17)

针对式(17)和ω的迟滞曲线采用极限环法[13]可以分别识别出迟滞参数ρ,σ,n。

2.3 参数识别结果

参照以上参数识别方法对O型钢丝绳隔振器三向动态特性模型的参数进行识别，其结果如表2所示。

2.4 有效性验证

为了验证改进模型和参数识别方法是否适用于描述O型钢丝绳隔振器剪切、横滚和拉压方向的动态特性，对试验所确定的3个承载方向迟滞环和根据参数识别结果所预测的迟滞环进行比较，如图6所示。

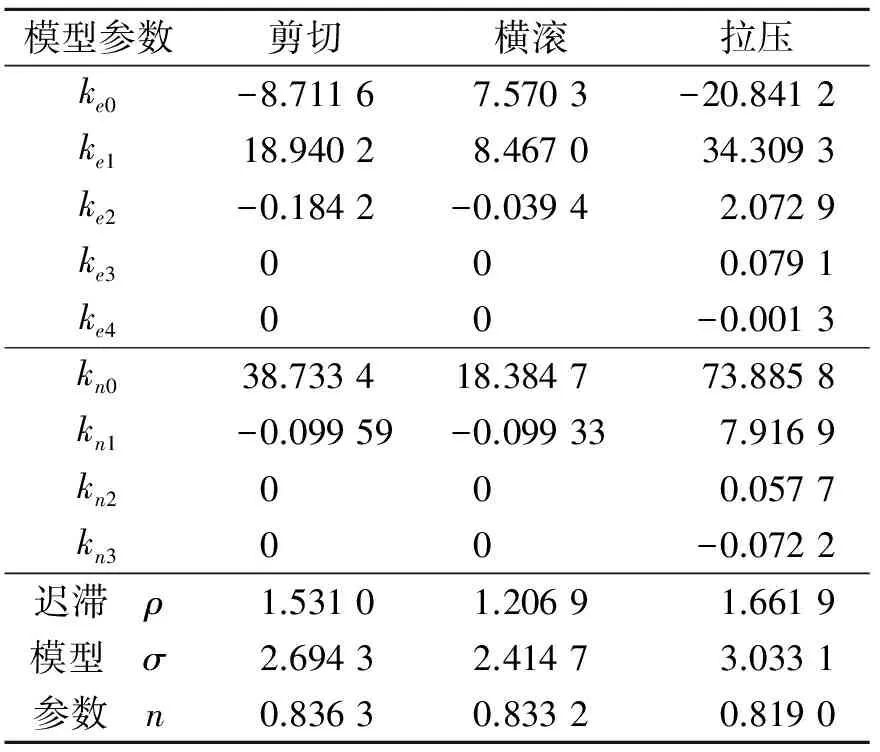
表2 模型参数识别结果

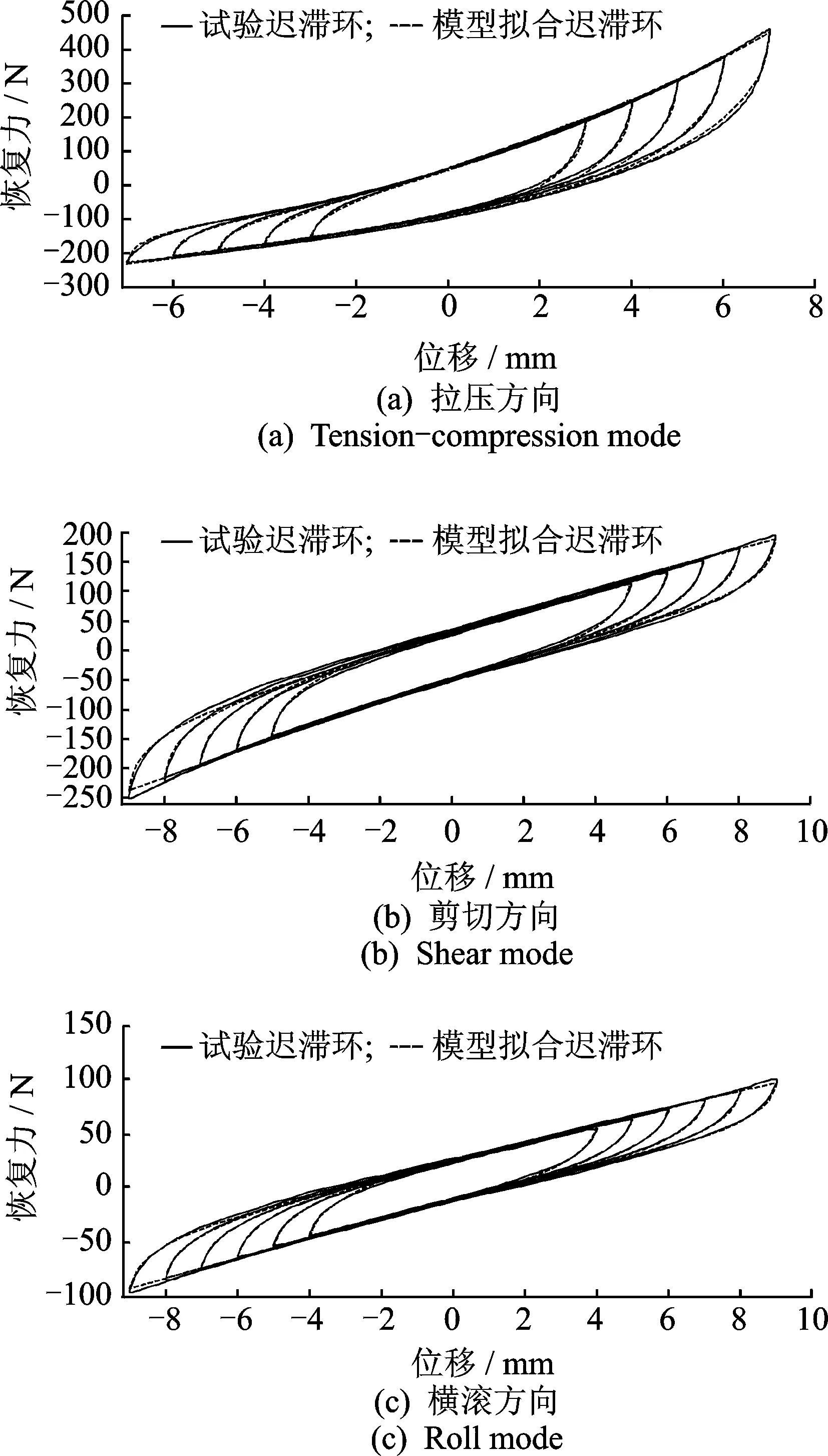
图6 模型预测和试验迟滞环比较图Fig.6 Comparison of the predicted and experimental hysteresis loops

为了评估改进模型和参数识别结果的有效性，分别计算3个承载方向预测迟滞环的均方根误差(RMSE)，其值越小，说明参数识别越精确。另外，改进的模型在对隔振器剪切、横滚和拉压方向进行动态特性描述时，根据具体试验数据以及曲线拟合情况，利用程序手动调整非线性弹性恢复力Fe和非线性放大因子Fn中多项式的阶数N和M的取值以及不同承载方向上待识别的试验迟滞环的位移幅值A，以便达到较好的拟合效果。N和M的取值以及相应的均方根误差(root mean square error,简称RMSE)值和位移幅值A如表3所示。

表3 模型预测迟滞环的拟合度指标RMSE

Tab.3 The RMSE of the predicted hysteresis loops

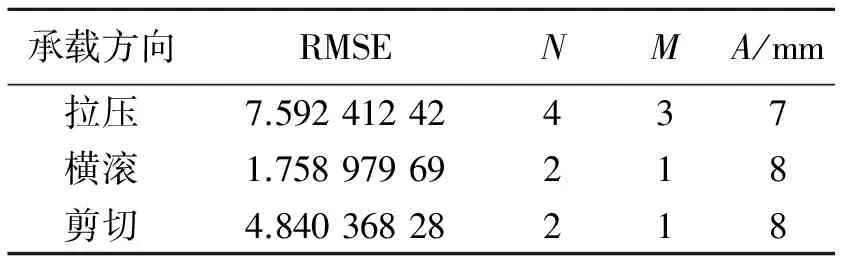
承载方向RMSENMA/mm拉压7．59241242437横滚1．75897969218剪切4．84036828218

由图6和表3可知，除了在转折点的地方存在差异之外，在剪切、横滚和拉压方向上的隔振器动态特性的试验曲线和模型预测曲线非常吻合。相对来讲，拉压方向的拟合情况差一些，横滚方向拟合情况最好。总之，该模型和相应参数识别方法比较适合描述该隔振器3个承载方向上的动态特性。

3 结论

1) 在剪切和横滚方向，得到了具有对称特性的试验迟滞环。由于在拉伸和压缩方向上钢丝绳内部股与股以及丝与丝之间不同的摩擦力的影响，在拉压方向上得到了具有非对称特性的试验迟滞环，而且随着激励幅值的增加，非对称迟滞特性表现的更加明显。尽管剪切和横滚的动态特性相似，然而横滚方向能量耗散小于剪切方向，拉压方向的能量耗散明显大于剪切和横滚方向，说明了该隔振器拉压方向的动态性能明显优于其他两个方向，是应用中的主要承载方向。另外，在测试频率段，隔振器在3个承载方向的动态特性均与频率无关。

2) 提出一种改进的归一化Bouc-Wen模型以及一种简单有效的两阶段参数识别方法来获取模型参数。通过选取Fe和Fn中多项式的阶数N和M以及相应参数的取值，分别用来描述剪切、横滚和拉压方向的动态迟滞特性。试验曲线和理论模型预测曲线吻合较好，该模型能够有效地描述O型钢丝绳隔振器非线性刚度和对称迟滞环以及非对称迟滞硬化重叠迟滞环的动态特性。

[1] Chaudhuri S , Kushwaha B. Wire rope based vibration isolation fixture for road transportation of heavy defence cargo[C]∥Vehicles Research & Development Establishment(VRDE). Maharas, India ：[s.n.], 2008:61-67.

[2] Demetriades G F, Constantinou M C, Reinhorn A M. Study of wire rope systems for seismic protection of equipment in buildings[J]. Engng Structs,1993, 15(5): 321-334.

[3] Massa G D, Pagano S, Rocca E, et al. Sensitive equipments on WRS-BTU isolators[J]. Meccanica, 2013, 48:1777-1790.

[4] Tinker M L, Cutchins M A. Damping phenomena in a wire rope vibration isolation system[J].Journal of Sound and Vibration, 1992,157(1): 7-18.

[5] 宣兆龙，赵瑾，刘亚超. 钢丝绳隔振器及其在弹药方舱中的应用[J]. 装备环境工程，2012，9(4)：79-81.

Xuan Zhaolong, Zhao Jin, Liu Yachao. Application of wire-rope vibration isolator in ammunition shelter[J].Equipment Environmental Engineering, 2012，9(4)：79-81. ( in Chinese)

[6] 国防科学技术工业委员会. GJB 6412-2008 舰船用钢丝绳隔振器规范[S].2008.

[7] 龚宪生，唐一科．一类迟滞非线性振动系统建模新方法[J].机械工程学报,1999，35(4):11-14．

Gong Xiansheng，Tang Yike．New method for modeling of a nonlinear vibration system with hysteresis characteristics[J].Journal of Mechanical Engineering,1999,35(4): 11-14．( in Chinese)

[8] 王珂，孙晓峰，于锋礼.钢丝网垫减振器的三维建模 [J]. 振动、测试与诊断， 2012， 32(6):931-934．

Wang Ke, Sun Xiaofeng, Yu Fengli. 3D modeling of steel-net pad damper[J]. Journal of Vibration, Measurement & Diagnosis，2012，32(6) : 931-934．( in Chinese)

[9] 唐斌，安西方，何鑫，等．橡胶钢丝绳复合隔振器动力学建模与参数识别[J].振动、测试与诊断， 2012，32(2):48-53．

Tang Bin，An Xifang，He Xin，et al． Dynamic model and parameter identification of rubber and wire-cable composite vibration isolator[J]．Journal of Vibration, Measurement & Diagnosis，2012， 32(2):48-53．( in Chinese)

[10] Bouc R. Forced vibration of mechanical systems with hysteresis [C]∥In the 4th Conference on Nonlinear Oscillations.Prague, Czech:Academia,1967:315.

[11] Wen Y K. Method for random vibration of hysteretic systems[J].Journal of the Engineering Mechanics Division, 1976,102(2): 249-263.

[12] Ikhouane F,Rodellar J. On the hysteretic Bouc-Wen model - part I:forced limit cycle characterization[J].Nonlinear Dynamics, 2005, 42(1): 63-78.

[13] Ikhouane F, Gomis- Bellmunt O A. limit cycle approach for the parametric identification of hysteretic systems[J]. Systems & Control Letters,2008, 57(8):663-669.

[14] Gerges R R. Model for the force-displacement relationship of wire rope springs[J]. Journal of Aerospace Engineering, 2008,21(1):1-9.

[15] Ni Y Q, Ko J M, Wong C W, et al. Modelling and identification of a wire-cable vibration isolator via a cyclic loading test, part 1:experiments and model development[J]. Proceedings of the Institution of Mechanical Engineers, Part I - Journal of Systems and Control Engineering,1999, 213(3):163-171.

[16] Gill P E, Murray W , Wright M H.Practical optimization[M]. London:Academic Press,1981:155-203.