基于相空间重构和ICA-R的轴承故障特征增强方法*

柏 林， 陆 超， 赵 鑫

(1.重庆大学机械传动国家重点实验室 重庆，400044) (2.武汉锐科光纤激光器有限责任公司 武汉，430000)



基于相空间重构和ICA-R的轴承故障特征增强方法*

柏 林1， 陆 超1， 赵 鑫2

(1.重庆大学机械传动国家重点实验室 重庆，400044) (2.武汉锐科光纤激光器有限责任公司 武汉，430000)

针对实测滚动轴承早期故障信号中故障特征频率成分微弱、难以识别及提取的问题，设计了一种结合相空间重构(phase-space reconstruction，简称PSR)和参考独立分量分析(independent component analysis with reference，简称ICA-R)的故障特征增强方法。利用相空间重构将一维时域信号拓展到高维，再进行参考独立分量分析，将所感兴趣的轴承故障特征频率成分进行增强。该方法相比传统频率提取方法具有效果好、对干扰频率抑制明显的特点。仿真结果和工程实测信号表明，该方法对滚动轴承早期故障特征提取有效可行，具有一定工程应用价值。

特征增强； 滚动轴承； 早期诊断； 相空间重构； 参考独立分量分析

引 言

滚动轴承早期故障常因故障特征频率过于微弱，被大量噪声和干扰频率所淹没，导致诊断不及时或误诊。传统的频率提取方法如经验模态分解(empirical mode decomposition,简称EMD)-包络分析[1]、小波-包络分析[2]、固有时间尺度分解(intrinsic time-scale decomposition,简称ITD)-包络分析[3]等方法均对分解所得高频成分进行分析。此类方法能够滤去低频成分的干扰，对包含在高频固有频率成分中的故障特征有一定的提取能力，然而当信号中故障特征微弱且存在大量干扰边频带时提取效果不理想。另外，以上方法在选择分解层数和判断包含故障成分的分量时需要较多的先验知识支持。

独立分量分析[4](independent component analysis，简称ICA)在特征提取方面具有很强的优势，能够消除信号中冗余的成分，对数据进行降维和分离。将其用于设备故障诊断中，对包含于信号中的微弱成分有较强的分离能力。然而ICA需要输入通道数目大于或者等于源信号数目，否则无法达到盲源分离的目的。实际故障诊断中，在传感器数量有限的情况下获得的往往是一维单通道时域信号。相空间重构[5]方法能够对信道进行多重复用，解决ICA对单通道输入欠定的问题，且保持重构信号对原始系统动力特征的反映。

然而，传统的ICA算法仍然存在信号输出顺序不定和计算效率低下的问题[6]，Lu等[7]针对以上问题提出了利用先验知识的参考独立分量分析(ICA-R)，该方法将已有先验知识嵌入到ICA的分离过程中，直接抽取需要的源信号，具有计算效率高、收敛结果优于传统ICA的优势。

笔者结合相空间重构和参考独立分量分析提出了PSR+ICA-R故障特征增强方法：将一维信号重构至高维，并利用ICA-R算法分解出重构相空间中与参考信号最接近的独立分量，以达到增强感兴趣的早期微弱故障频率成分的目的。

1 相空间重构

(1)

其中：m为重构维数；τ为延迟时间；xT为x矩阵的转置；i满足1≤i≤N-(m-1)τ。

m和τ的选择是重构相空间质量的关键参数。G-P法、伪临近点法、CAO法均可选择合适的重构维数m。延迟时间τ的选择多采用自相关函数法或互信息法[8]。考虑到对于实测信号多存在较为严重的背景噪声，噪声在一定程度上影响了重构维数m和延迟时间τ的正确选择，因而对相空间重构参数的选取方法要求一定的抗噪特性。

选取延迟时间τ时，由于自相关法本质上是属于处理线性问题的范畴，不符合相空间重构对非线性问题的处理要求，且难于向更高维度拓展，因此笔者选择文献[9]中的结合平均位移法与自相关法的去偏复自相关函数Rx(τ)来选取τ

(2)

当Rx(τ)第1次通过零点时所对应的时间延迟即为τ。由于噪声成分本质上是不相关的，因而该方法有较强的抗噪能力。

选取重构维数m时，G-P法对数据量要求较大且需要不含噪声，实际运用中并不实用。伪临近点法是较为有效的计算方法，而CAO法是在伪临近点法基础上考虑τ值后的改进方法。笔者选取CAO法的E1(m)判据确定重构维数m，利用了其对噪声不敏感的特性[10]。

CAO法需要已知延迟时间τ，随后从1开始依次增大重构维数m，计算E1(m)函数

(3)

其中

(4)

随着m的增加，当E1(m)逐渐趋于稳定时所对应的m即为最佳重构维数。

2 参考独立分量分析

与传统ICA方法存在的区别是，ICA-R定义了输出源y(t)与参考信号r(t)的接近性度量函数ε(y,r)，使得ICA-R算法在不断的迭代修正后仅得到一个全局最优解w*，最终使分离出的信号y(t)=w*Tx(t)是与参考信号最接近的一个期望源[11]，算法原理如图1所示。

图1 一单元ICA-R算法原理图Fig.1 Algorithm of one-unit ICA-R

Lin等[12]在ICA-R的基础上提出了一单元快速ICA-R算法(fast one-unit ICA-R)，用预白化处理代替原始算法中的求逆过程，提高了算法的收敛速度。一元ICA-R算法是如下约束最优化问题

其中：J(y)为Hyvärinen提出的负熵对照函数的一元形式；ξ为阙值。

接近性度量函数可选为ε(y,r)=E{(y-r)2}或-E{yr}，且在权重向量w=w*时取得最小值。

针对式(5)中g(w)≤0引入松弛变量z，将其改为等式形式g(w)+z2=0，对该式引入广义拉格朗日函数后代入牛顿学习算法，利用固定点迭代更新w

(6)

其中

文献[12]所提方法即在每次迭代过程中将权重向量归一化

(10)

3 基于相空间重构和ICA-R的特征提取方法

合理选择重构维数与延迟时间对保持信号对原始系统动力特征的反映非常重要。通过笔者所选方法进行相空间重构时由于复自相关函数法和CAO法都需要先验知识，因此采取先根据经验取合适的重构维数m，再通过复自相关函数求取τ，最后用CAO法验证先前估算的重构维数的合理性。

在重构好的高维空间中，ICA算法基于负熵准则寻求一个使得各通道分量尽可能独立的解混矩阵w。由于参考信号的引入，一单元ICA-R算法获得的分离信号是最接近参考信号的独立成分，这样突出了所感兴趣的故障频率成分，使得所得增强信号有实际的物理意义。

具体的PSR+ICA-R算法流程步骤如下：

1) 信号预处理；

2) 根据经验估计重构维数m；

3) 利用去偏复自相关函数Rx(τ)来选取τ；

4) 利用上一步骤所得的τ通过CAO法计算重构维数m′；

5) 比较m′和m，若m′>m，需要重新选择较大的重构维数，再重复步骤2～4；若m′≤m，即所估计m满足重构条件，能够反映出原始系统的特征；

6) 利用选定的m和τ重构相空间X；

7) 根据需要提取的成分构造参考信号；

8) 将重构好的相空间X和参考信号一起输入ICA-R解混。

4 仿真分析

为了验证算法的正确性，取仿真冲击信号

(11)

其中：指数频率B=1 kHz，载波频率f1=3 kHz，指数系数T=mod(tΔt,1/fm)，Δt为采样间隔，fm=100 Hz为调制频率。

对该冲击信号叠加幅值较大的余弦分量作为干扰频率成分

6cos(2π100t)+2cos(2π250t)

(12)

在信号中加入了信噪比SNR=10db的高斯白噪声。采样率为20 kHz，采样点数为10 000点。

其时域信号如图2所示(fi=finterference为干扰频率，fs=fshock为冲击频率)。

如图2(b)所示，将该仿真信号进行包络解调，可以看到需要提取的冲击信号fs较为微弱且高次谐波分量几乎看不到，其他干扰频率成分强。

根据前文所提方法，首先根据经验选取合理的重构维数m，在此选择m=9。利用重构维数求去偏复自相关函数Rx(τ)，如图3所示。

第1个最近零点位置为τ=23。将其作为CAO法的先验条件求取重构维数，分别用2范数和无穷范数求取m。计算结果如图4所示，在m=9之后E1(m)函数趋于稳定且接近于1，说明重构空间已经充分展开，最临近点的平均距离不再随着重构维数的增加而有明显的变化。因此根据经验所取的m是合理的。值得一提的是初次选择较大的m虽然不会影响重构空间对原始系统特征的反映，而且后期计算若m在较小处即稳定，仍然可以使用预估的较大的m进行相空间重构，但是冗余的重构空间会增大不必要的计算量。

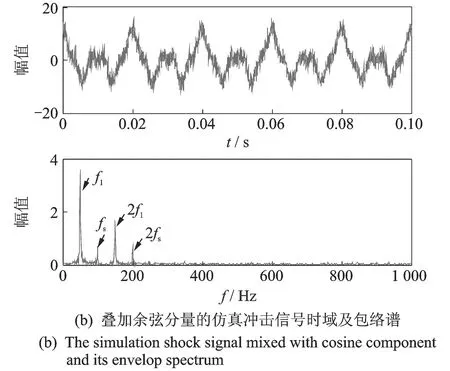
图2 仿真信号图Fig.2 The simulation signals

图3 去偏复自相关函数Rx(τ)变化图Fig.3 Results of self-correlation with offset eliminated function Rx(τ)

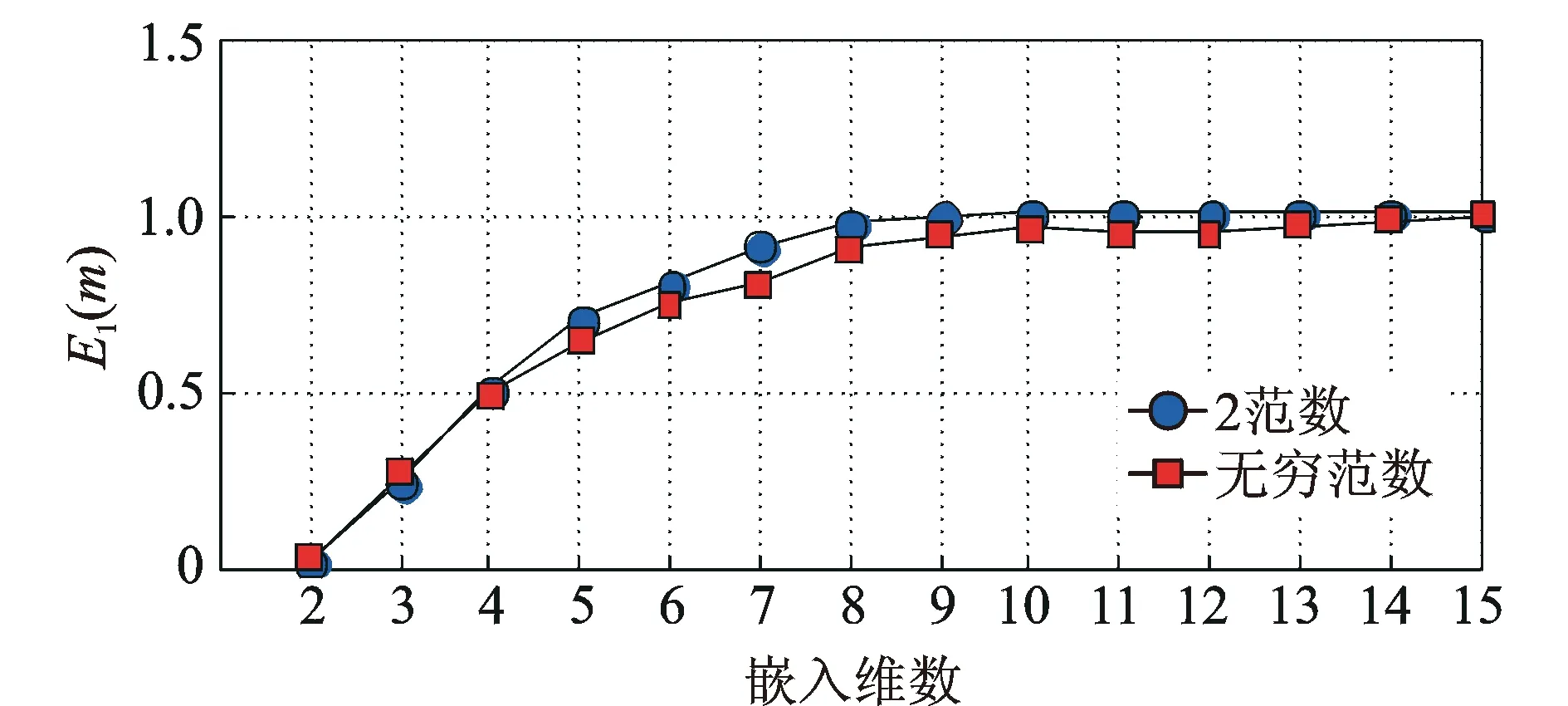
图4 CAO法E1(m)函数变化图Fig.4 Results of E1(m) of CAO method

重构得到时域矩阵X后，需要构造相应的参考信号。参考信号的选择常采用与需分离的源信号同频率同相位的方波信号，如图5所示。

图5 参考信号Fig.5 Reference signal

由于方波的引入，接近性度量函数ε(y,r)对谐波成分也较为敏感，在提取同频率源信号时，若阙值ξ选择合理，该算法对谐波成分也具有一定的提取能力。将参考信号和重构所得X一同输入ICA-R进行解混，输出通道时域波形和频谱如图6所示。

图6 ICA-R输出信号频谱Fig.6 Output spectrum of ICA-R

观察频谱易发现，所欲提取的频率成分fs和其倍频成分被很好的增强出来，且干扰成分fi得到抑制。

5 滚动轴承早期故障特征增强

为了验证该方法在实测轴承早期故障频率增强中的作用，笔者选取了美国Case Western Reserve University[13]提供的公开滚动轴承故障数据。实验中所选择的滚动轴承故障特征频率如表1所示。

选择B007_2组滚动体故障信号中的驱动端加速度传感器数据，该组数据中滚动体故障直径为0.177 8 mm，电机转速为1 750 r/min。由表2计算得到的滚动体故障特征频率fb=137.5 Hz。实fr为转频。

表1 滚动轴承故障特征频率表

测信号时域和频谱如图7所示，时域信号中冲击成分不明显。

图7 滚动轴承振动加速度信号时域和频谱Fig.7 Rolling bearing acceleration signal and its spectrum

取中心频率为3 300 Hz、带宽为800 Hz进行包络解调，包络谱如图8所示。图中可以看到一些保持架频率成分以及较微弱的滚动体故障频率基频fb和倍频成分，但周围存在大量噪声与调制频率成分，不便于观察和判断故障类型，故障特征有待被增强。

图8 滚动轴承信号包络谱图Fig.8 Envelop spectrum of the rolling bearing

由于实际检测中故障未知，因此依次选择与不同类型故障频率同频率的方波信号作为参考信号。然而上面所提仿真信号所包含的频率成分的相位是已知的，构造参考信号时选择同频率、同相位方波信号即可。实测信号中对于需要分离的频率成分相位未知，对于参考方波而言，其与需要提取的故障频率成分的相位差总在[0,π)范围内，因而实际分析中采用依次改变方波初始相位并代入ICA-R尝试获得最优解的方法。

图9 不同参考频率所得ICA-R输出频谱图Fig.9 Output spectrums of ICA-R with different references

将重构矩阵X和各个参考信号输入ICA-R解混，输出通道的频谱如图9所示。从图9中可以看到，滚动体故障频率fb以及它们的倍频成分得到增强，成为较明显的幅值分量。虽然频谱上出现了内外圈故障频率，然而考虑到频谱上出现的滚动体故障特征频率和倍频，以及低频区的保持架频率和倍频，且滚动体故障频率附近有被保持架和因不平衡力因素所联合调制的自振频率，另外滚动体故障会引起内外圈故障频率的掺入。这些现象都说明了该故障属于滚动体故障。

对比传统的ITD-包络解调和小波-包络解调方法提取故障特征频率成分，此类方法都选择包含故障信息的高频段成分的分量，其中小波方法选择db4小波进行8层分解。经观察，选择包含所需提取故障信息的PR1和D1分量，其包络谱如图10所示。

图10 ITD-包络和小波-包络方法Fig.10 ITD-envelop and wavelet-envelop methods

表2中，PSR+ICA-R方法对1倍滚珠故障频率的增强效果是其余两种方法的2～3倍，且在增强谐波分量时也具有较好的效果。综合以上结果表明，笔者所提方法相比传统ITD-包络和小波-包络方法具有更好的微弱故障增强效果。

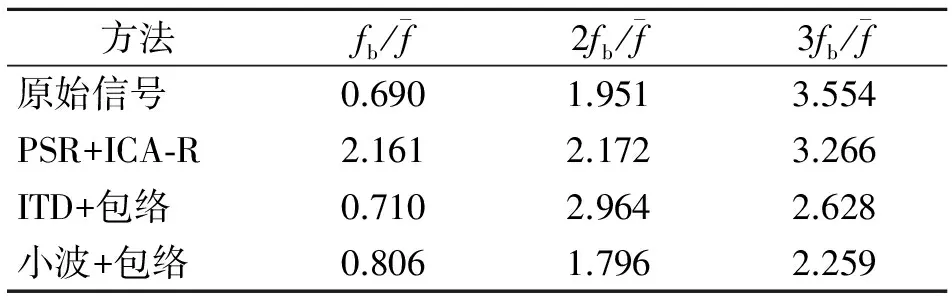
表2 对比各方法增强效果量化关系表

另取某现场实测的滚动轴承内圈故障信号，用本方法增强内圈故障频率。由于内圈信号在传递至传感器时会有较大的损耗和干扰，原始信号的包络谱如图11(a)所示，故障特征不明显，噪声和干扰很大。在增强后所得图11(b)中，可以看出内圈故障被清晰地显示出来，其余干扰频率被明显地抑制，增强效果好。

图11 某轴承内圈故障信号增强处理图Fig.11 Inner-race signal enhanced by PSR+ICA-R methods

6 结束语

笔者将相空间重构与ICA-R方法结合，提出了PSR+ICA-R故障特征增强方法，把单通道时间序列信号重构到高维作为虚拟输入通道，解决了独立分量分析的欠定问题。将重构后的信号进行参考独立分量分析，有效地提取出包含在原始信号中的感兴趣的成分，省去了传统ICA分解后需要进一步筛选所需独立分量的步骤。将该算法运用到滚动轴承早期故障特征的增强中，对较弱频率分量增强效果明显。对比传统ITD-包络和小波-包络提取结果，该方法增强效果更好，对边频和其他干扰频率抑制明显。在工程运用中提取、判断滚动轴承早期故障具有一定的实用价值。由于ICA类方法存在的幅值欠定问题，将本方法运用于实际工程中的定量检验时存在一定的困难，需要参考原始信号中的故障频率幅值来统一修正增强后的信号。今后的研究中加把幅值修正过程嵌入到ICA-R算法中，能使该方法获得更强的实际应用能力。

[1] 唐宏宾, 吴运新, 滑广军, 等. 基于 EMD 包络谱分析的液压泵故障诊断方法[J]. 振动与冲击, 2012, 31(9): 44-48.

Tang Hongbin, Wu Yunxin, Hua Guangjun, et al . Fault diagnosis of pump using EMD and envelope spectrum analysis[J]. Journal of Vibration and Shock, 2012, 31(9): 44-48. (in Chinese)

[2] 李宏坤, 赵长生, 周帅，等. 基于小波包—坐标变换的滚动轴承故障特征增强方法[J]. 机械工程学报, 2011, 47(19):74-80.

Li Hongkun, Zhao Changsheng, Zhou Shuai, et al. Fault feature enhancement method for rolling bearing based on wavelet packet-coordinate transformation[J]. Chinese Journal of Mechanical Engineering, 2011, 47(19):74-80. (in Chinese)

[3] 程军圣, 李海龙, 杨宇. 改进ITD和能量矩在齿轮故障诊断中的应用[J]. 振动、测试与诊断, 2013, 33(6): 954-959.

Cheng Junsheng, Li Hailong, Yang Yu. Based on the improved ITD and energy moment to diagnose the gear[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(6): 954-959. (in Chinese)

[4] Hyvärinen A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Trans. Neural Networks, 1999, 10(3): 626-634.

[5] 章立军, 张利欣, 阳建宏，等. 基于平稳小波变换的相空间重构方法[J]. 振动、测试与诊断, 2012, 32(6): 981-985.

Zhang Lijun, Zhang Lixin, Yang Jianhong, et al. Phase space reconstruction based on stationary wavelet transform[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(6): 981-985. (in Chinese)

[6] 李镜, 林秋华. 一种应用幅值信息的一单元定点复数 ICA-R 算法[J]. 电子与信息学报, 2008, 30(11): 2666-2669.

Li Jing, Lin Qiuhua. One-unit fixed-point complex-valued ICA-R algorithm using magnitude information[J]. Journal of Electronics & Information Technology, 2008, 30(11): 2666-2669. (in Chinese)

[7] Lu Wei, Rajapakse J C. ICA with reference[J]. Neuro Computing, 2006, 69(16-18) : 2244- 2257．

[8] 陈铿, 韩伯棠. 混沌时间序列分析中的相空间重构技术综述[J]. 计算机科学, 2005, 32(4):67-70.

Chen Keng, Han Botang. A survery of state space reconstruction of chaotic time series analysis[J]. Computer Science, 2005, 32(4):67-70. (in Chinese)

[9] 马红光, 李夕海 , 王国华. 相空间重构中嵌入维和时间延迟的选择[J]. 西安交通大学学报,2004,38(4):335-338.

Ma Hongguang, Li Xihai, Wang Guohua. Selection of embedding dimension and delay time in phase space reconstruction[J]. Journal of Xi′an Jiaotong University, 2004, 38(4):335-338. (in Chinese)

[10]许岩. 含噪混沌时间序列相空间重构参数估计[D]. 重庆:重庆大学, 2013.

[11]张杰, 张周锁, 朱冠汶，等. 多元消减约束独立分量分析及其在振源贡献量计算中的应用[J]. 机械工程学报, 2014, 50(5):57-64.

Zhang Jie, Zhang Zhousuo, Zhu Guanwen, et al. Multi-unit deflation constraint independent component analysis and its application to source contribution estimation[J]. Chinese Journal of Mechanical Engineering, 2014, 50(5):57-64. (in Chinese)

[12]Lin Qiuhua, Zheng Yourui, Yin Fuliang, et al. A fast algorithm for one-unit ICA-R[J]. Information Sciences, 2007, 177(5):1265-1275．

[13]Bearing Data Center, Case Western Reserve University. Seeded fault test data [DB/OL]. [2015-12-25]http://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website./

10.16450/j.cnki.issn.1004-6801.2016.06.010

*国家自然科学基金资助项目(51675064,51475052)；中央高校基本科研业务费资助项目(106112016CDJIR115502)

2014-11-15；

2014-12-24

TP206.3； TH132

柏林，男，1972年11月生，教授、博士生导师。主要研究方向为虚拟仪器与信号处理。曾发表《Measurement system for wind turbines noises assessment based on LabVIEW》(《Measurement》2011，Vol. 44，No.2)等论文。 E-mail: bolin0001@aliyun.com